【排序算法】-- 深入理解桶排序算法
概述
在计算机科学中,排序算法是一种对数据进行有序排列的重要技术。桶排序(Bucket Sort)是一种常见的排序算法,它通过将数据分到有限数量的桶中,并对每个桶中的数据分别排序,最后按照顺序将所有桶中的数据合并起来,从而实现整体有序。桶排序的时间复杂度取决于桶的数量以及桶内使用的排序算法,通常情况下表现良好。

桶排序原理
桶排序的基本思想是将待排序的元素分到有限数量的桶中,然后对每个桶中的数据进行排序,最后按照桶的顺序依次将所有桶中的数据合并起来,即可得到有序的结果。
具体步骤如下:
- 划分桶: 首先确定桶的数量,并将待排序的元素根据一定的规则分到相应的桶中。这个规则可以是根据元素的大小、值的范围或者其他特定的条件。
- 对每个桶排序: 对每个桶中的数据进行排序。可以使用任何适合的排序算法,通常情况下使用的是插入排序或者快速排序等简单且高效的排序算法。
- 合并桶: 将排好序的每个桶中的数据按照桶的顺序依次合并起来,即可得到最终的有序结果。
桶排序的优缺点
优点:
- 高效性: 桶排序通常具有较快的排序速度,尤其在数据分布均匀的情况下表现更佳。
- 稳定性: 桶排序可以稳定地进行排序,即相等元素的相对位置不会发生改变。
- 适用性: 桶排序适用于一定范围内的整数或浮点数排序,特别是对于外部排序问题有很好的应用。
缺点:
- 空间消耗: 桶排序可能需要额外的空间来存储桶,尤其是当元素分布不均匀时可能会造成部分桶空间浪费。
- 不稳定性: 如果在桶内使用的排序算法不稳定,可能会导致最终排序结果的不稳定性。

Java 实现
下面是使用 Java 实现桶排序的示例代码:
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;public class BucketSortJava {public static void bucketSort(double[] arr) {int n = arr.length;List<Double>[] buckets = new ArrayList[n];// Initialize bucketsfor (int i = 0; i < n; i++) {buckets[i] = new ArrayList<>();}// Put elements into bucketsfor (double num : arr) {int bucketIndex = (int) (num * n);buckets[bucketIndex].add(num);}// Sort each bucketfor (List<Double> bucket : buckets) {Collections.sort(bucket);}// Merge bucketsint index = 0;for (List<Double> bucket : buckets) {for (double num : bucket) {arr[index++] = num;}}}public static void main(String[] args) {double[] arr = {0.8, 0.5, 0.2, 0.3, 0.7, 0.6, 0.1, 0.4, 0.9};bucketSort(arr);System.out.println("Sorted array:");for (double num : arr) {System.out.print(num + " ");}}
}
Python 实现
下面是使用 Python 实现桶排序的示例代码:
def bucket_sort(arr):n = len(arr)buckets = [[] for _ in range(n)]# Put elements into bucketsfor num in arr:bucket_index = int(num * n)buckets[bucket_index].append(num)# Sort each bucketfor bucket in buckets:bucket.sort()# Merge bucketsindex = 0for bucket in buckets:for num in bucket:arr[index] = numindex += 1arr = [0.8, 0.5, 0.2, 0.3, 0.7, 0.6, 0.1, 0.4, 0.9]
bucket_sort(arr)
print("Sorted array:")
print(arr)
JavaScript 实现
下面是使用 JavaScript 实现桶排序的示例代码:
function bucketSort(arr) {const n = arr.length;const buckets = Array.from({ length: n }, () => []);// Put elements into bucketsarr.forEach(num => {const bucketIndex = Math.floor(num * n);buckets[bucketIndex].push(num);});// Sort each bucketbuckets.forEach(bucket => {bucket.sort((a, b) => a - b);});// Merge bucketslet index = 0;buckets.forEach(bucket => {bucket.forEach(num => {arr[index++] = num;});});
}const arr = [0.8, 0.5, 0.2, 0.3, 0.7, 0.6, 0.1, 0.4, 0.9];
bucketSort(arr);
console.log("Sorted array:");
console.log(arr);
总结
桶排序是一种简单而有效的排序算法,通过将数据分到有限数量的桶中,然后对每个桶中的数据进行排序,最后合并所有桶中的数据,可以实现整体有序。虽然桶排序在某些情况下可能会占用较多的空间,但在特定的应用场景下,它具有较快的排序速度和稳定的性能表现。本文介绍了桶排序算法的原理、优缺点,并提供了 Java、Python 和 JavaScript 三种常见编程语言的实现示例。
在实际应用中,桶排序通常用于对一定范围内的整数或浮点数进行排序,特别是当待排序的数据分布相对均匀时,桶排序可能会达到较好的效果。例如,当需要对一组考试成绩进行排序时,如果成绩范围在0到100之间,并且每个分数段内的人数相差不大,那么桶排序可能是一个不错的选择。
除了以上提到的优缺点外,还有一些其他需要注意的事项:
- 桶的数量选择: 桶的数量需要根据具体情况进行选择,通常情况下桶的数量与待排序的元素个数相当,但也可以根据实际情况进行调整。
- 桶内排序算法选择: 桶内排序算法可以选择适合的任何排序算法,常见的有插入排序、快速排序等,选择合适的排序算法可以提高桶排序的效率。
- 稳定性问题: 如果在桶内排序时使用的排序算法不稳定,可能会导致最终排序结果的不稳定性,需要注意。
总的来说,桶排序是一种简单而有效的排序算法,适用于一定范围内的数据排序问题。通过合理的桶划分和桶内排序算法选择,可以在实际应用中达到较好的排序效果。但需要注意的是,桶排序可能会占用较多的空间,因此在某些情况下可能不适用于内存受限的环境。
相关文章:

【排序算法】-- 深入理解桶排序算法
概述 在计算机科学中,排序算法是一种对数据进行有序排列的重要技术。桶排序(Bucket Sort)是一种常见的排序算法,它通过将数据分到有限数量的桶中,并对每个桶中的数据分别排序,最后按照顺序将所有桶中的数据…...
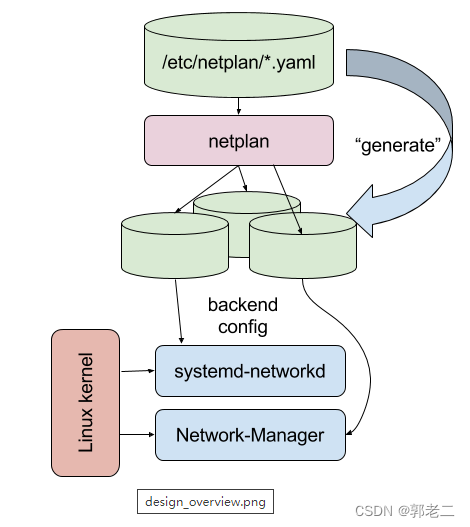
【Linux】Ubuntu使用Netplan配置静态/动态IP
1、说明 Ubuntu 18.04开始,Ubuntu和Debian移除了以前的ifup/ifdown命令和/etc/network/interfaces配置文件,转而使用ip link set或者/etc/netplan/01-netcfg.yaml模板和sudo netplan apply命令实现网络管理。 Netplan 是抽象网络配置描述器,用于配置Linux网络。 通过netpla…...
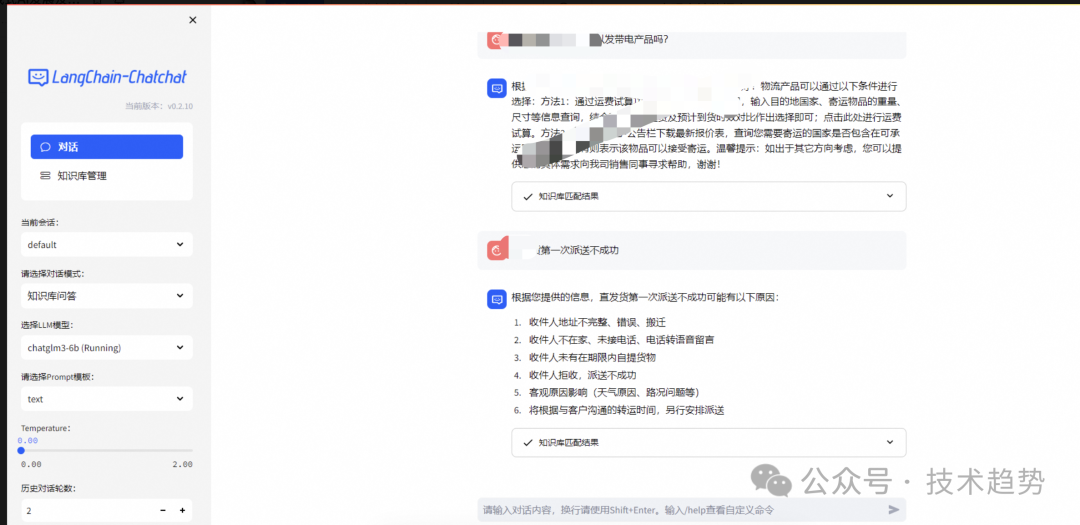
chatGLM3+chatchat实现本地知识库
背景 由于客服存在大量的问题为FAQ问题,需要精准回复客户,所以针对此类精准问题,通过自建同量数量库进行回复。 落地方案 通过chatGLM3-6Blangchain-chatchatbge-large-zh实现本地知识库库。 注意:相关介绍和说明请看官网~ 配置要…...
webpack5零基础入门-11处理html资源
1.目的 主要是为了自动引入打包后的js与css资源,避免手动引入 2.安装相关包 npm install --save-dev html-webpack-plugin 3.引入插件 const HtmlWebpackPlugin require(html-webpack-plugin); 4.添加插件(通过new方法调用) /**插件 *…...
el-input设置max、min无效的解决方案
目录 一、方式1:type“number” 二、方式2:oninput(推荐) 三、计算属性 如下表所示,下面为官方关于max,min的介绍: el-input: max原生属性,设置最大值min原生属性&a…...
)
C语言经典面试题目(十八)
1、如何在C语言中实现堆排序算法? 堆排序是一种利用堆数据结构进行排序的算法。它的基本思想是首先将待排序的数组构建成一个最大堆(或最小堆),然后逐步将堆顶元素与堆中最后一个元素交换,并重新调整堆,使…...

[数据集][目标检测]零售柜零食检测数据集VOC+YOLO格式5422张113类
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):5422 标注数量(xml文件个数):5422 标注数量(txt文件个数):5422 标注…...

Flask vs. Django:选择适合你的Web开发框架【第134篇—Flask vs. Django】
👽发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【点击进入巨牛的人工智能学习网站】。 Flask vs. Django:选择适合你的Web开发框架 在选择一个适合你项目的Web开发框架…...
的概念和用法吗?在Spring中,如何使用事务管理?)
你能解释一下Spring AOP(面向切面编程)的概念和用法吗?在Spring中,如何使用事务管理?
你能解释一下Spring AOP(面向切面编程)的概念和用法吗? Spring AOP(面向切面编程)是Spring框架中一个非常重要的功能模块,它允许开发者通过预编译方式和运行期动态代理来实现程序功能的统一维护。AOP并不是…...

时序分解 | Matlab实现GWO-CEEMDAN基于灰狼算法优化CEEMDAN时间序列信号分解
时序分解 | Matlab实现GWO-CEEMDAN基于灰狼算法优化CEEMDAN时间序列信号分解 目录 时序分解 | Matlab实现GWO-CEEMDAN基于灰狼算法优化CEEMDAN时间序列信号分解效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.CEEMDAN方法的分解效果取决于白噪声幅值权重(Nstd)和噪声添…...
:利用Jasypt对数据库连接进行加密)
Spring Boot(七十):利用Jasypt对数据库连接进行加密
1 Jasypt简介 Jasypt(Java Simplified Encryption)是一个专注于简化Java加密操作的工具。它提供了一种简单而强大的方式来处理数据的加密和解密,使开发者能够轻松地保护应用程序中的敏感信息,如数据库密码、API密钥等。 Jasypt的设计理念是简化加密操作,使其对开发者更加…...

Mysql设计规范
主键推荐默认用递增字符串大小合理设置数据库默认字段: 主键、创建人、创建时间、修改人、修改时间、逻辑删除(可选)、乐观锁(可选)冗余字段: 严禁冗余变更字段;例如: 创建人名称,租…...

Vue3项目部署安装
Vue3ts部署 查看官网安装项目vue3的命令(四个)其中有: yarn create vuelatest 我执行时遇到报错,可能是我yarn版本不是最新 的问题, 改用这个命令去掉latest即可 yarn create vue 新项目先要安装yarn依赖,才能yarn …...
Oracle P6 Professional 配置连接数据库总结
前言 P6 Professional作为Oracle P6计划管理系统的重要套件之一,其操作出色,体检佳,是非常多的计划工程师跟踪项目进度计划的辅助工具。自20年前,Professional一直在不断的演变更新,以适应当前的新技术,从…...
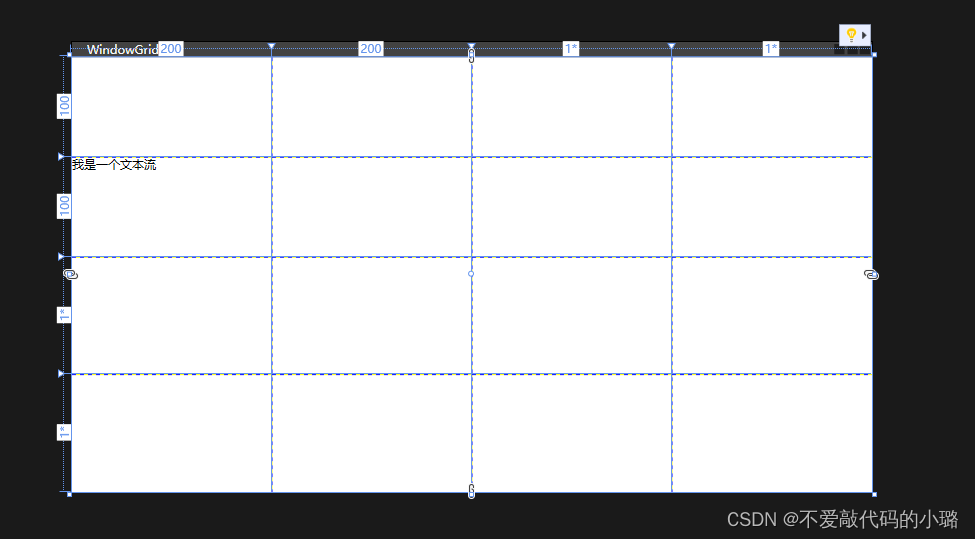
WPF —— Grid网格布局
1 :Grid网格布局简介 Grid为WPF中最常用的布局容器, 作为View中的主要组成部分, 负责框架中整体的页面布局。 2:网格标签Grid.ColumnDef Grid.ColumnDefinitions自定义列 只能设置宽度 不能设置高度ColumnDefinition 每一个列可以设置宽度,…...
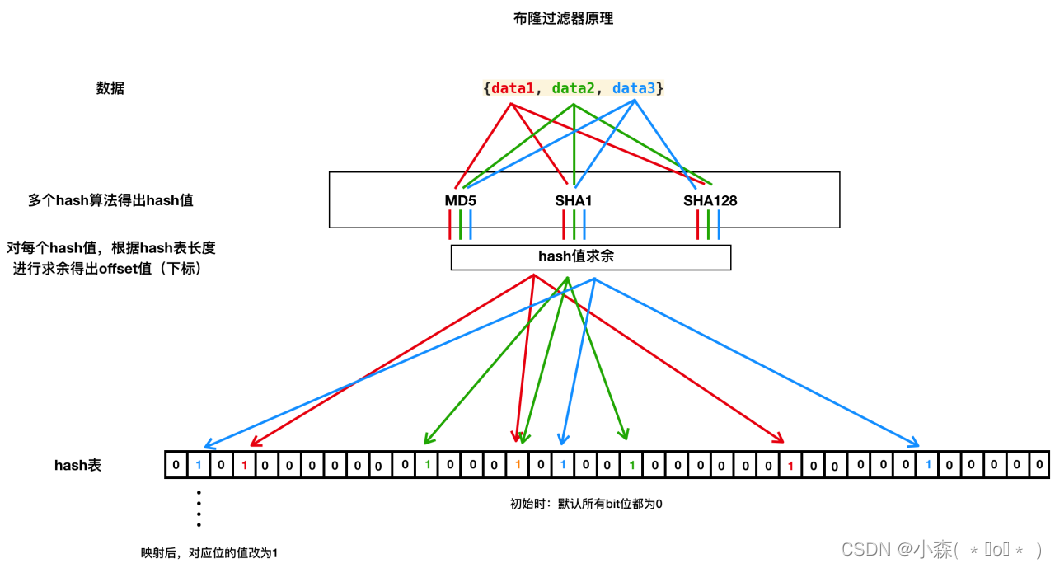
爬虫的去重
去重基本原理 爬虫中什么业务需要使用去重 防止发出重复的请求防止存储重复的数据 在爬取网页数据时,避免对同一URL发起重复的请求,这样可以减少不必要的网络流量和服务器压力,提高爬虫的效率,在将爬取到的数据存储到数据库或其…...
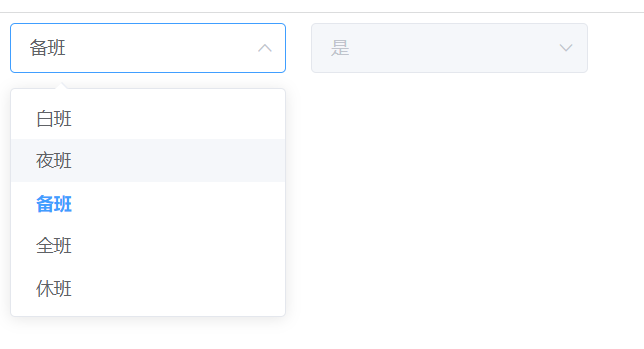
elementUI两个select单选框联动
实现需求:两个单选框内容两栋,在选择第一个时,第二个选框能自动更新对应选项。且在切换第一个选项内容时,第二个选框会被清空且切换到新的对应选项。 设置值班班次和备班情况两个选项 ,完整代码如下: <…...
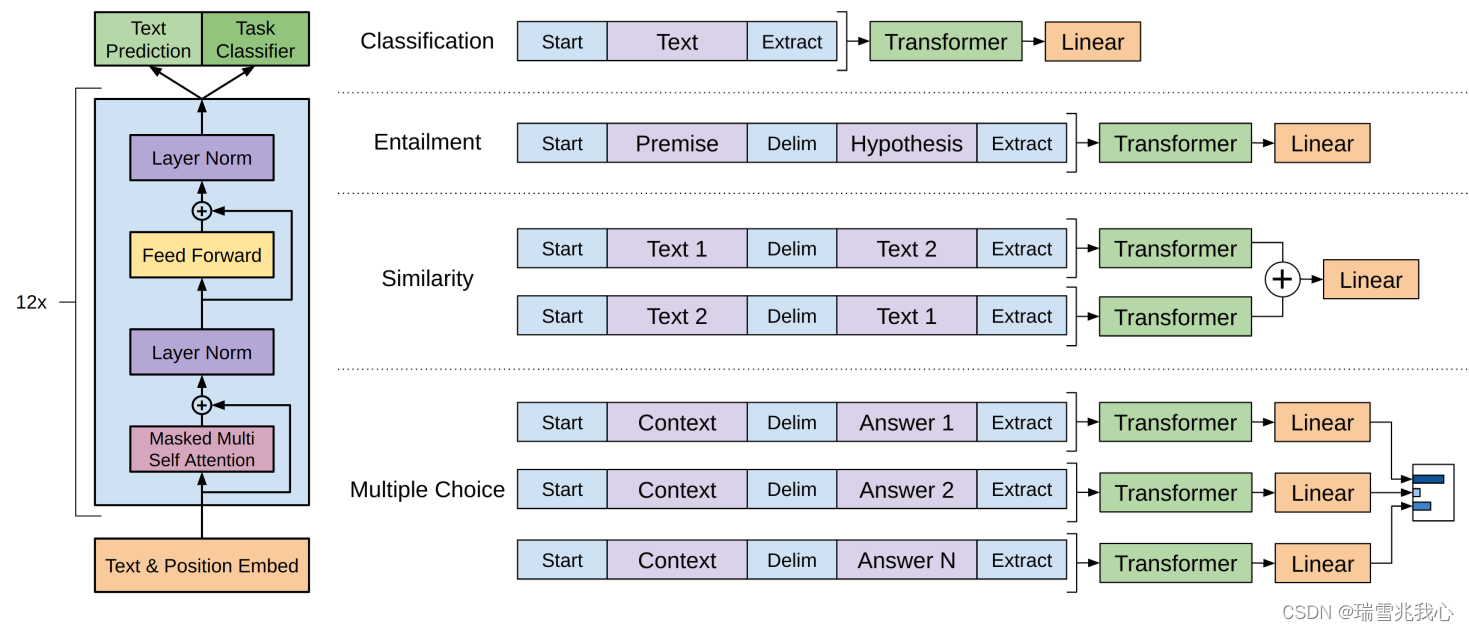
十四、GPT
在GPT-1之前,传统的 NLP 模型往往使用大量的数据对有监督的模型进行任务相关的模型训练,但是这种有监督学习的任务存在两个缺点:预训练语言模型之GPT 需要大量的标注数据,高质量的标注数据往往很难获得,因为在很多任务…...

五款优秀的FTP工具
一、WinSCP WinSCP是一个Windows环境下使用SSH的开源图形化SFTP客户端。同时支持SCP协议。它的主要功能就是在本地与远程计算机间安全的复制文件。.winscp也可以链接其他系统,比如linux系统。 官网:https://winscp.net/ 二、FileZilla FileZilla是一个免费开源的…...

十八、软考-系统架构设计师笔记-真题解析-2022年真题
软考-系统架构设计师-2022年上午选择题真题 考试时间 8:30 ~ 11:00 150分钟 1.云计算服务体系结构如下图所示,图中①、②、③分别与SaaS、PaaS、IaaS相对应,图中①、②、③应为( )。 A.应用层、基础设施层、平台层 B.应用层、平台层、基础设施层 C.平…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...


