当前位置：首页 > news >正文

信号与系统学习笔记——信号的分类

news 2026/2/8 20:42:21

一、确定与随机

二、连续与离散

三、周期与非周期

判断是否为周期函数

离散信号的周期

结论

四、能量与功率

定义

结论

五、因果与反因果

六、阶跃函数

定义

性质

七、冲激函数

定义

重要关系

作用

一、确定与随机

确定信号：可以确定时间函数表示的信号。

随机信号：不可以确定时间函数表示的信号。

二、连续与离散

连续时间信号：连续时间范围内（-∞<t<+∞）有定义的信号，简称连续信号。若其函数值也连续，常称为模拟信号（值域连续）。

图2.1 连续信号

离散时间信号：仅在一些离散的瞬间才有定义的信号，简称离散信号。当取值为规定数值时，常称为数字信号（值域不连续）。

图2.2 数字信号

连续信号变为离散信号：（AD转换）：如果想让一个连续信号进入计算机，需要让连续信号（模拟信号）变为离散信号（数字信号）。这是我们会用到连续采样的方法。

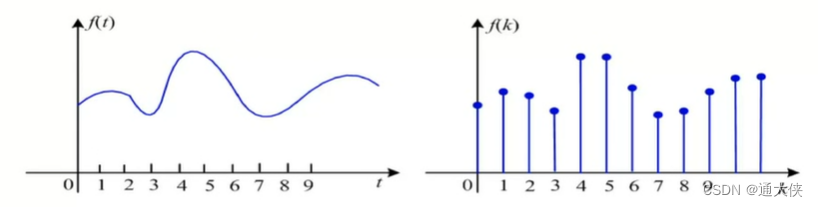
图2.3 连续信号变为离散信号

离散信号变为连续信号（DA转换）：此法主流有两种表示。第一种是零阶保持法；第二种是分段线性法。

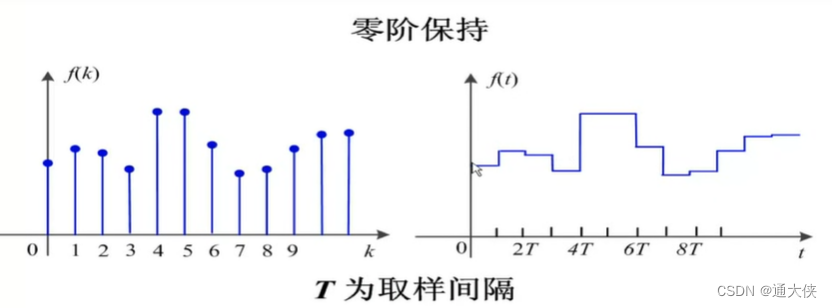
图2.4 零阶保持法

图2.5 分段线性法

三、周期与非周期

周期与非周期的概念我们已经非常熟悉了，这里不再过多赘述。

判断是否为周期函数

m个周期函数合成为一个新函数的周期，表示为 $T=m_{i}T_{i}$ $(i=1,2,3...)$

判断方法：两个周期信号的周期分别为 $T_{1}$ 与 $T_{2}$ ，若 $T_{1}$ 与 $T_{2}$ 是有理数，则周期信号之和仍然是周期信号，其周期为 $T_{1}$ 与 $T_{2}$ 的最小公倍数。

例题：判断函数 $f_{1}(t)=sin2t+cos3t$ 是否为周期函数，若是，周期是多少？

$T_{1}$ ： $\frac{2\pi }{\omega}=\pi$

$T_{2}$ ： $\frac{2\pi }{\omega}=\frac{2\pi}{3}$

所以 $f_{1}(t)$ 是周期信号，其周期为2π

拓展：若函数是三个周期函数合成的，怎样判断它是否为周期函数，函数的周期是多少？

假设合成后的函数是周期为T的周期函数，那么可得到：

$m_{1}:m_{2}:m_{3}=\frac{T}{T_{1}}:\frac{T}{T_{2}}:\frac{T}{T_{3}}$

消去分子T，再乘2π，可得到：

$m_{1}:m_{2}:m_{3}=\frac{2\pi }{T_{1}}:\frac{2\pi}{T_{2}}:\frac{2\pi}{T_{3}}=\omega _{1}:\omega _{2}:\omega _{3}$

三个以上周期信号的合成仍适用。

离散信号的周期

f(k)是离散周期信号，N为周期。表示为： $f(k)=f(k+mN),m=0,\pm 1,\pm2...$

例题：判断正弦序列f(k)=sin(βk）是否为周期信号，若是，确定其周期，式中β为数字角频率，单位：rad。

解：假设f(k)是周期信号，那么可得到：

f(k)=sin(βk)=sin(βk+2mπ)，m=0，±1，±2...

$=sin[\beta (k+\frac{2m\pi }{\beta })]$

$=sin[\beta (k+mN)]$

结论

① $\frac{2\pi }{\beta }$ 为整数时，正弦序列具有周期 $N=\frac{2\pi }{\beta }$

② $\frac{2\pi }{\beta }$ 为有理数时，正弦序列仍具有周期性，但周期是 $N=M\frac{2\pi }{\beta }$ ，M取使N为整数的最小整数。

③ $\frac{2\pi }{\beta }$ 为无理数时，正弦序列为非周期序列。

连续正弦信号一定是周期信号，而正弦序列不一定是周期序列；两连续周期信号之和不一定是周期信号，而两周期序列之和一定是周期序列。

四、能量与功率

定义

图4.1 能量的定义

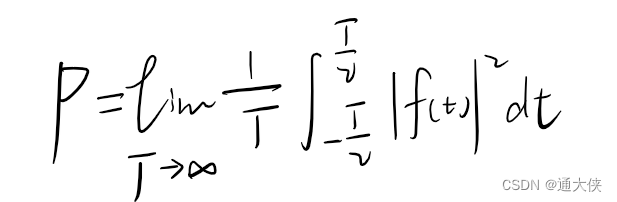
图3.2 平均功率的定义

能量有限信号：信号的能量E<∞，简称能量信号，此时平均功率P=0。

功率有限信号：信号的功率P<∞，简称功率信号，此时能量E=∞。

结论

①时限信号（仅在有限时间区间不为零）为能量信号；

②周期信号属于能量信号；

③非周期信号可能是能量信号，也可能是功率信号；

④有些信号既不是能量信号也不是功率信号，比如指数函数 $f(t)=e^{t}$ 。

五、因果与反因果

因果信号： $t= 0$ ，f(t)=0的信号（即t0时接入系统的信号），比如阶跃信号。

反因果信号： $t\geqslant 0$ ，f(t)=0的信号（除0信号外）。

六、阶跃函数

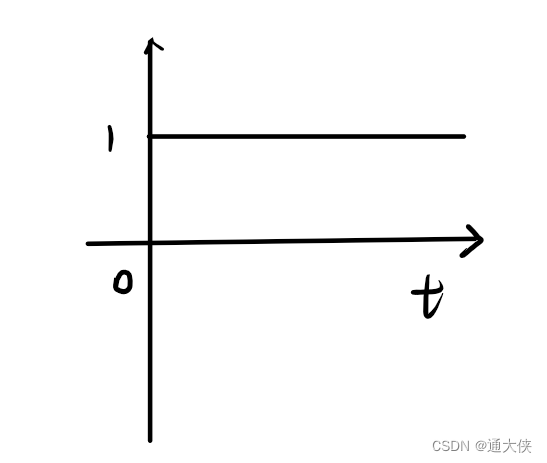
图6.1 单位阶跃函数

定义

图6.2 阶跃函数的定义

性质

①表示分段常量信号；

②表示信号的作用区间；

③积分 $\int_{-oo}^{t}\varepsilon (\tau )d\tau =t\varepsilon (t)$

七、冲激函数

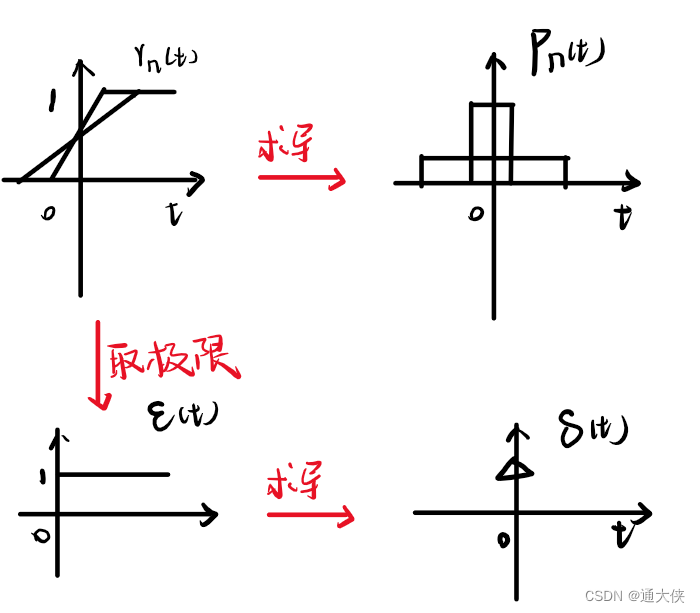
图7.1 几种函数图形

定义

冲激函数是奇异函数，它是对强度极大，作用时间极短的物理量的理想化模型，由狄拉克提出。

图7.2 冲激函数的函数

理解：高度无穷大，宽度无穷小，面积为1的对称窄脉冲

图7.3

图7.3中间的Pn(t)叫“门函数”

重要关系

$\delta (t)=\frac{d\varepsilon (t)}{dt}$

$\varepsilon (t)=\int_{-oo}^{t}\delta (\tau )d\tau$

作用

冲激函数可以描述间断点的导数

图7.4

信号与系统学习笔记——信号的分类

目录一、确定与随机二、连续与离散三、周期与非周期判断是否为周期函数离散信号的周期结论四、能量与功率定义结论五、因果与反因果六、阶跃函数定义性质七、冲激函数定义重要关系作用一、确定与随机确定信号：可以确定时间函数…...

编程日记 2024/3/18 12:53:50

PyTorch深度学习实战（39）——小样本学习

PyTorch深度学习实战（39）——小样本学习 0. 前言1. 小样本学习简介2. 孪生网络2.1 模型分析2.2 数据集分析2.3 构建孪生网络 3. 原型网络3. 关系网络小结系列链接 0. 前言小样本学习 (Few-shot Learning) 旨在解决在训练集中只有很少样本的情况下进行分…...

编程日记 2024/3/18 12:50:48

论文阅读——Vision Transformer with Deformable Attention

Vision Transformer with Deformable Attention 多头自注意力公式化为： 第l层transformer模块公式化为： 在Transformer模型中简单地实现DCN是一个non-trivial的问题。在DCN中，特征图上的每个元素都单独学习其偏移，其中HWC特征图上…...

编程日记 2024/3/18 12:48:46

AJAX概念和axios使用、URL、请求方法和数据提交、HTTP协议、接口、form-serialize插件

AJAX概念和axios使用 AJAX概念 AJAX就是使用XMLHttpRequest对象与服务器通信，它可以使用JSON、XML、HTML和text文本等格式发送和接收数据，AJAX最吸引人的就是它的异步特性，也就是说它可以在不重新刷新页面的情况下与服务器通信，…...

编程日记 2024/3/18 12:46:45

【R语言基础操作】

🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972 个人介绍: 研一｜统计学｜干货分享擅长Python、Matlab、R等主流编程软件累计十余项国家级比赛奖项，参与研究经费10w、40w级横向文…...

编程日记 2024/3/18 12:43:42

sqlite 常见命令表结构

在 SQLite 中，将表结构保存为 SQL 具有一定的便捷性和重要性，原因如下便捷性： 备份和恢复：将表结构保存为 SQL 可以方便地进行备份。如果需要还原或迁移数据库，只需执行保存的 SQL 脚本，就可以重新创建表…...

编程日记 2024/3/18 12:42:42

基于深度学习的车辆检测技术

基于深度学习的车辆检测技术是现代智能交通系统的重要组成部分，它利用计算机视觉和机器学习算法，特别是深度学习模型，来识别和定位图像或视频中的车辆。这项技术广泛应用于自动驾驶、交通监控、违章抓拍等多个领域。深度学习车辆检测技术的…...

编程日记 2024/3/18 12:41:40

MyBatis 之三：配置文件详解和 Mapper 接口方式

配置文件 MyBatis 的配置文件是 XML 格式的，它定义了 MyBatis 运行时的核心行为和设置。默认的配置文件名称为 mybatis-config.xml，该文件用于配置数据库连接、事务管理器、数据源、类型别名、映射器（mapper 文件）以及其他全局属性…...

编程日记 2024/3/18 12:39:39

【PyTorch】基础学习：一文详细介绍 torch.load() 的用法和应用

【PyTorch】基础学习：一文详细介绍 torch.load() 的用法和应用 🌈 个人主页：高斯小哥 🔥 高质量专栏：Matplotlib之旅：零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程&#x1f44…...

编程日记 2024/3/18 12:37:36

配置全局事务 DATABASES {default: {ENGINE: django.db.backends.mysql,NAME: mydb,USER:root,PASSWORD:pass,HOST:127.0.0.1,PORT:3306,ATOMIC_REQUESTS: True, # 全局开启事务，绑定的是http请求响应整个过程# (non_atomic_requests可局部实现不让事务控制)} } …...

编程日记 2024/3/18 12:35:35

PC-DARTS: PARTIAL CHANNEL CONNECTIONS FOR MEMORY-EFFICIENT ARCHITECTURE SEARCH

PC-DARTS：用于内存高效架构搜索的部分通道连接论文链接：https://arxiv.org/abs/1907.05737 项目链接：https://github.com/yuhuixu1993/PC-DARTS ABSTRACT 可微分体系结构搜索(DARTS)在寻找有效的网络体系结构方面提供了一种快速的解决方案…...

编程日记 2024/3/18 12:34:34

git的下载与安装

下载首先，打开您的浏览器，并输入Git的官方网站地址点击图标进行下载下载页面会列出不同操作系统和平台的Git安装包。根据您的操作系统（Windows、macOS、Linux等）和位数（32位或64位），选择适…...

编程日记 2024/3/18 12:32:32

windows文档格式转换的实用工具

大家好，我是爱编程的喵喵。双985硕士毕业，现担任全栈工程师一职，热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

编程日记 2024/3/18 12:29:29

四级缓存实现

CommandLineRunner接口的run方法什么是多级缓存？多级缓存就是充分利用请求处理的每个环节，分别添加缓存，减轻Server端的压力，提升服务性能。一级缓存：1.CDN：内容分发网络二级缓存：2.NGINX+Lua脚本+OpenResty服务器负载均衡反向代理【静态和转发】三级缓存：J…...

编程日记 2024/3/18 12:28:28

程序员如何规划职业赛道？

在快速发展的信息技术时代，程序员作为数字世界的构建者，面临着前所未有的职业选择和发展机会。选择合适的职业赛道，不仅关乎个人职业发展的高度和速度，更影响着个人职业生涯的满意度和幸福感。本文将从自我评估与兴趣探索、市场需…...

编程日记 2024/3/18 12:27:27

蓝桥杯day3刷题日记--P9240 冶炼金属

P9240 [蓝桥杯 2023 省 B] 冶炼金属经典二分，先在第一组中找到最小值，在利用最小值限制范围寻找最大值 #include <iostream> #include <algorithm> using namespace std; int n,kk; int m[10001],num[10001]; int maxs,mins;bool check1…...

编程日记 2024/3/18 12:26:26

Mybatis-xml映射文件与动态SQL

xml映射文件动态SQL <where><if test"name!null">name like concat(%,#{name},%)</if><if test"username!null">and username#{username}</if></where>  <!-- …...

编程日记 2024/3/18 12:25:25

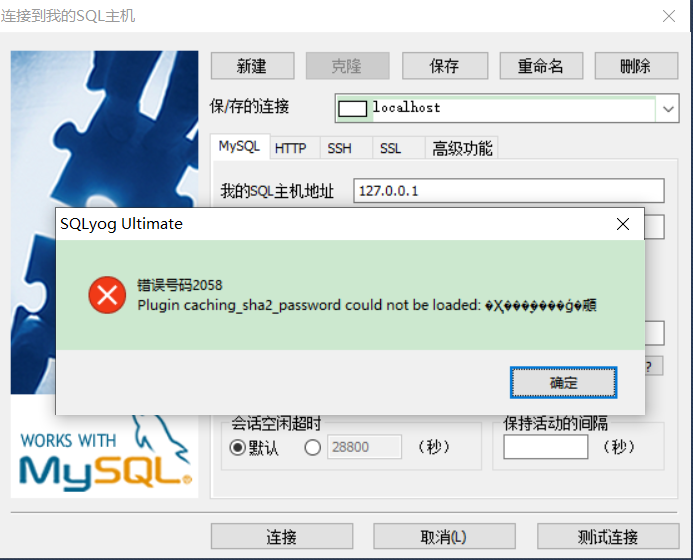
MySQL_数据库图形化界面软件_00000_00001

目录 NavicatSQLyogDBeaverMySQL Workbench可能出现的问题 Navicat 官网地址： 英文：https://www.navicat.com 中文：https://www.navicat.com.cn SQLyog 官网地址： 英文：https://webyog.com DBeaver 官网地址&…...

编程日记 2024/3/18 12:22:22

流媒体学习之路(WebRTC)——FEC逻辑分析（6）

流媒体学习之路(WebRTC)——FEC逻辑分析（6） —— 我正在的github给大家开发一个用于做实验的项目 —— github.com/qw225967/Bifrost目标：可以让大家熟悉各类Qos能力、带宽估计能力，提供每个环节关键参数调节接口并实现一个json全…...

编程日记 2024/3/18 12:21:22

command failed: npm install --loglevel error --legacy-peer-deps

在使用vue create xxx创建vue3项目的时候报错。解决方法，之前使用的https://registry.npm.taobao.org 证书过期更换镜像地址即可操作如下： 1.cd ～2.执行rm .npmrc3. sudo npm install -g cnpm --registryhttp://registry.npmmirror.com…...

编程日记 2024/3/18 12:16:16

19c补丁后oracle属主变化，导致不能识别磁盘组

补丁后服务器重启，数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后，存在与用户组权限相关的问题。具体表现为，Oracle 实例的运行用户（oracle）和集…...

编程新知 2026/2/8 4:37:10

Spark 之入门讲解详细版（1）

1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室（Algorithms, Machines, and People Lab）开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目，8个月后成为Apache顶级项目，速度之快足见过人之处&…...

编程新知 2026/2/5 4:17:31

R语言AI模型部署方案：精准离线运行详解

R语言AI模型部署方案：精准离线运行详解一、项目概述本文将构建一个完整的R语言AI部署解决方案，实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点： 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

编程新知 2025/12/6 1:56:35

FFmpeg 低延迟同屏方案

引言在实时互动需求激增的当下，无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作，还是游戏直播的画面实时传输，低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架，凭借其灵活的编解码、数据…...

编程新知 2025/11/4 6:26:59

Debian系统简介

目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍软件包管理工具dpkg dpkg核心指令详解安装软件包卸载软件包查询软件包状态验证软件包完整性手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核的 Linux 发行版&#xff…...

编程新知 2026/2/1 13:41:09

抖音增长新引擎：品融电商，一站式全案代运营领跑者

抖音增长新引擎：品融电商，一站式全案代运营领跑者在抖音这个日活超7亿的流量汪洋中，品牌如何破浪前行？自建团队成本高、效果难控；碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

编程新知 2026/2/1 5:45:17

反射获取方法和属性

Java反射获取方法在Java中，反射（Reflection）是一种强大的机制，允许程序在运行时访问和操作类的内部属性和方法。通过反射，可以动态地创建对象、调用方法、改变属性值，这在很多Java框架中如Spring和Hiberna…...

编程新知 2025/11/9 2:57:17

Java 二维码

Java 二维码 **技术：**谷歌 ZXing 实现首先添加依赖 <dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

编程新知 2025/9/6 16:22:45

QT3D学习笔记——圆台、圆锥

类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体（对象或容器）QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质（定义颜色、反光等）QFirstPersonC…...

编程新知 2026/1/29 5:26:37

mac 安装homebrew (nvm 及git)

mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤通用： 方法一：使用 Homebrew 安装 Git（推荐） 步骤如下：打开终端（Terminal.app） 1.安装 Homebrew…...

编程新知 2026/1/30 4:58:21

一、确定与随机

二、连续与离散

三、周期与非周期

判断是否为周期函数

离散信号的周期

结论

四、能量与功率

定义

结论

五、因果与反因果

六、阶跃函数

定义

性质

七、冲激函数

定义

重要关系

作用

相关文章：