代码随想录算法训练营第14天 part01 | 二叉树理论基础篇
代码随想录
二叉树理论基础篇
二叉树的种类
二叉树有两种主要的形式:满二叉树和完全二叉树
满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。

这棵二叉树为满二叉树,也可以说深度为k,有2^k-1个节点的二叉树。
完全二叉树
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(h从1开始),则该层包含 1~ 2^(h-1) 个节点。
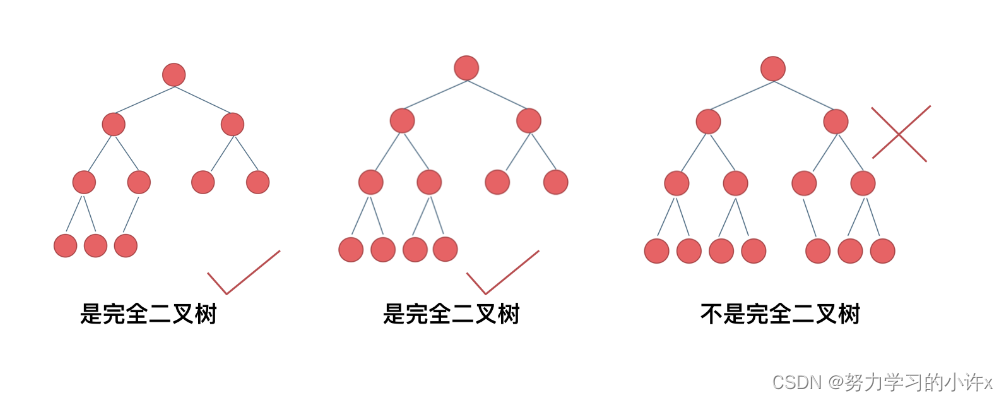
优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系。
二叉搜索树
二叉搜索树是有数值的了,二叉搜索树是一个有序树。
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树也分别为二叉排序树
平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
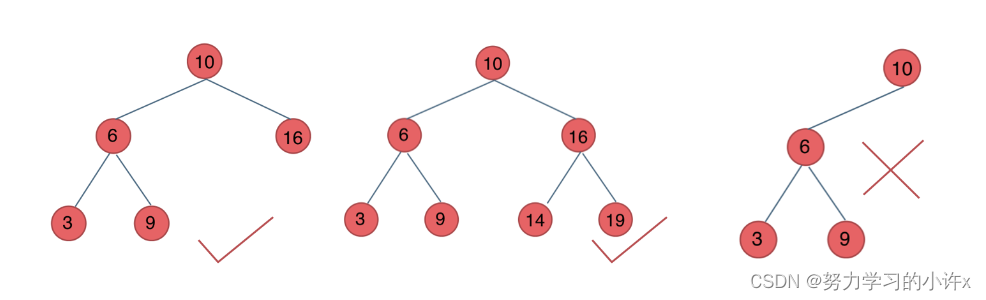
C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作时间时间复杂度是logn,注意我这里没有说unordered_map、unordered_set,unordered_map、unordered_set底层实现是哈希表。
二叉树的存储
二叉树可以链式存储,也可以顺序存储。
那么链式存储方式就用指针, 顺序存储的方式就是用数组。

顺序存储的方式如图:
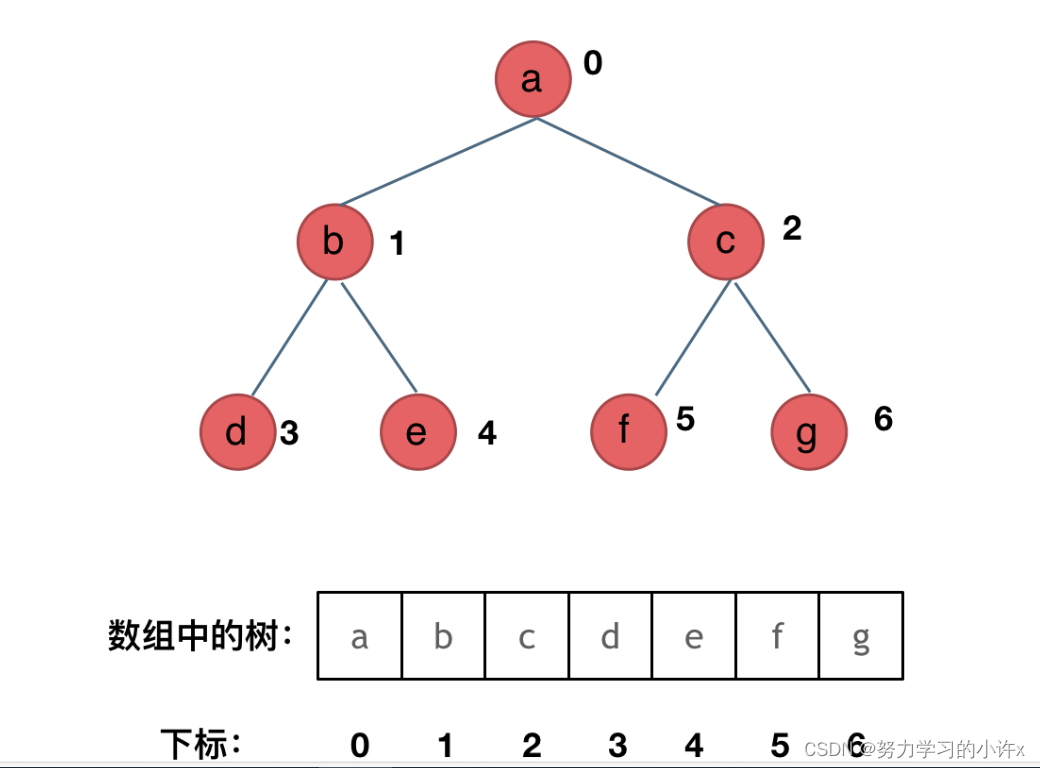
用数组来存储二叉树如何遍历的呢?
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
二叉树的遍历
二叉树主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
深度优先遍历
1、前序遍历(递归法,迭代法)2、中序遍历(递归法,迭代法)3、后序遍历(递归法,迭代法)
广度优先遍历
层次遍历(迭代法)
这里前中后,其实指的就是中间节点的遍历顺序
前序遍历:中左右
中序遍历:左中右
后序遍历:左右中
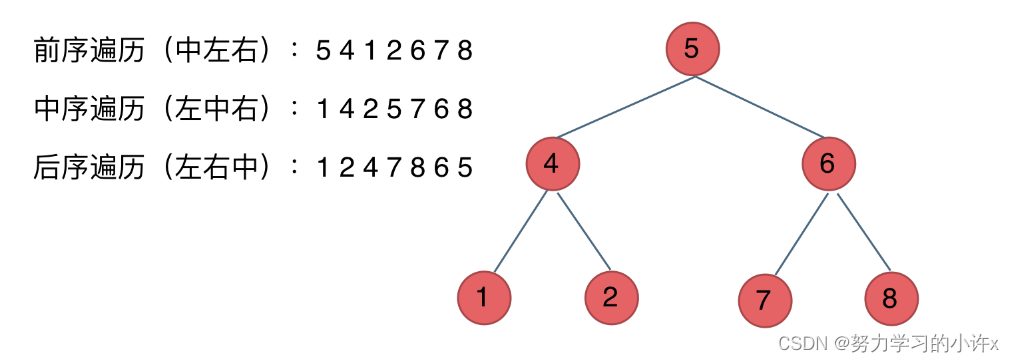
最后再说一说二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
之前我们讲栈与队列的时候,就说过栈其实就是递归的一种实现结构,也就说前中后序遍历的逻辑其实都是可以借助栈使用递归的方式来实现的。
而广度优先遍历的实现一般使用队列来实现,这也是队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树。
在现场面试的时候 面试官可能要求手写代码,所以数据结构的定义以及简单逻辑的代码一定要锻炼白纸写出来。
public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}
相关文章:

代码随想录算法训练营第14天 part01 | 二叉树理论基础篇
代码随想录 二叉树理论基础篇 二叉树的种类 二叉树有两种主要的形式:满二叉树和完全二叉树 满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。 这棵二叉树为满二叉树…...

async与defer的区别
原文解释 async vs defer attributes - Growing with the Web...

奇数乘积(C语言)
一、运行结果; 二、源代码; # define _CRT_SECURE_NO_WARNINGS # include <stdio.h>int main() {//初始化变量值;int i 1;int j 3;//循环运算;while (j < 12){//运算;i i * j;//改变数值;j 2…...

中文分词库:jieba的词性对照表
jieba词性对照表 字母词性a形容词ad副形词ag形容词性语素an名形词b区别词c连词d副词dg副词素e叹词f方位词g语素h前接成分i成语j简称略称k后接成分l习用语m数词mq数量词n名词ng名词性语素nr人名ns地名nt机构团体名nz其他专名o拟声词p介词q量词r代词rg代词性语素rr人称代词rz指示…...
Linux:git的基础操作
git的下载 版本控制系统一般分为两种,集中式版本控制系统,分布式版本控制系统 什么是集中式版本控制系统:版本库集中存放在中央服务器,工作时候使用自己的电脑,当工作时候在中央服务器上拉取最新版本的代码,…...

【华为OD机试】CPU 算力分配【C卷|100分】
【华为OD机试】-真题 !!点这里!! 【华为OD机试】真题考点分类 !!点这里 !! 题目描述 现有两组服务器A和B,每组有多个算力不同的CPU,其中 A[i] 是 A 组第 i 个CPU的运算能力, B[i] 是 B组 第 i 个CPU的运算能力。 一组服务器的总算力是各CPU的算力之和。 为了让两组服务器…...

挑战杯 机器视觉目标检测 - opencv 深度学习
文章目录 0 前言2 目标检测概念3 目标分类、定位、检测示例4 传统目标检测5 两类目标检测算法5.1 相关研究5.1.1 选择性搜索5.1.2 OverFeat 5.2 基于区域提名的方法5.2.1 R-CNN5.2.2 SPP-net5.2.3 Fast R-CNN 5.3 端到端的方法YOLOSSD 6 人体检测结果7 最后 0 前言 ǵ…...

基于Spring Boot的社区便民服务管理系统的设计与实现
摘 要 二十一世纪我们的社会进入了信息时代,信息管理系统的建立,大大提高了人们信息化水平。传统的管理方式对时间、地点的限制太多,而在线管理系统刚好能满足这些需求,在线管理系统突破了传统管理方式的局限性。于是本文针对这一…...
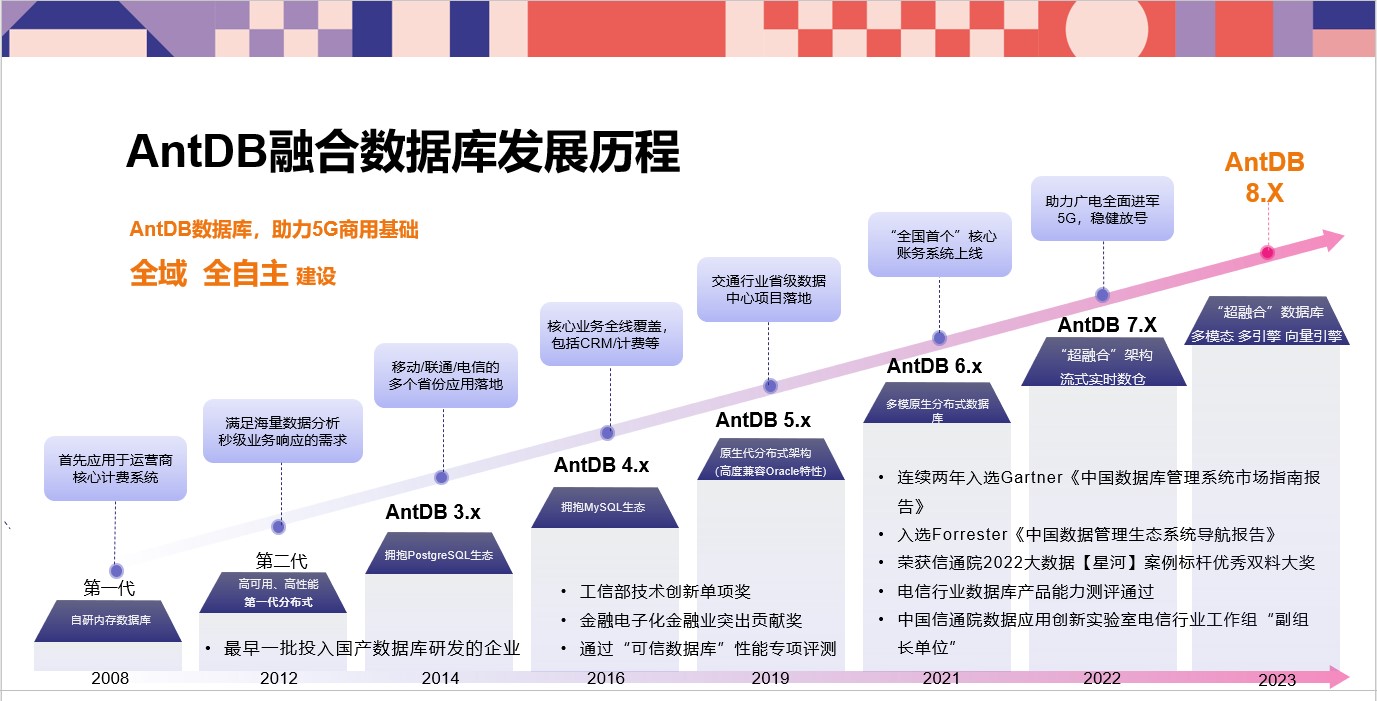
亚信安慧AntDB:数字化创新背后的数据力量
亚信安慧AntDB的“融合实时”的特性,不仅使得数据库具备了更强大的适应性,更让企业在不同业务场景下能够更好地实现业务目标,释放出更大的商业价值。融合实时的特性让AntDB具有了高度灵活性和实时性,使其能够满足企业在不同业务需…...

Matplotlib数据可视化实战-1数据可视化Matplotlib基础
1.1绘图的一般过程: 1.导入相关库 2.生成、读入或计算得到数据; 3.根据需要绘制折线图、散点图、柱状图、饼状图、雷达图、箱线图、三维曲线/曲面以及极坐标系图形; 4.根据需要设置图形属性; 5.显示或保存绘图结果。 例如&…...

信也科技发布消费者权益保护2023年度报告: 科技驱动、服务为先、合作共建社会化消保体系
3月15日消费者权益日当天,信也科技发布《消费者权益保护2023年度报告》(下称《报告》,消费者权益保护简称“消保”)。该报告为信也科技消保委员会成立后首份公开披露的消保工作年度总结。《报告》显示,信也科技通过智能…...

REDHAWK——连接(续)
文章目录 前言一、突发 IO1、数据传输①、输入②、输出 2、突发信号相关信息 (SRI)3、多输出端口4、使用复数数据①、在 C 中转换复数数据 5、时间戳6、端口统计①、C 二、消息传递1、消息生产者①、创建一个消息生产者②、发送消息 2、消息消费者①、创建消息消费者②、注册接…...

9.Python从入门到精通—Python 字符串格式化,三引号,Unicode 字符串
9.Python从入门到精通—Python 字符串格式化,三引号,Unicode 字符串 Python 字符串格式化Python 三引号Unicode 字符串创建 Unicode 字符串Python 的字符串内建函数 Python 字符串格式化 Python中的字符串格式化是指将一个字符串中的占位符替换为指定的值。Python中有多种字符串…...
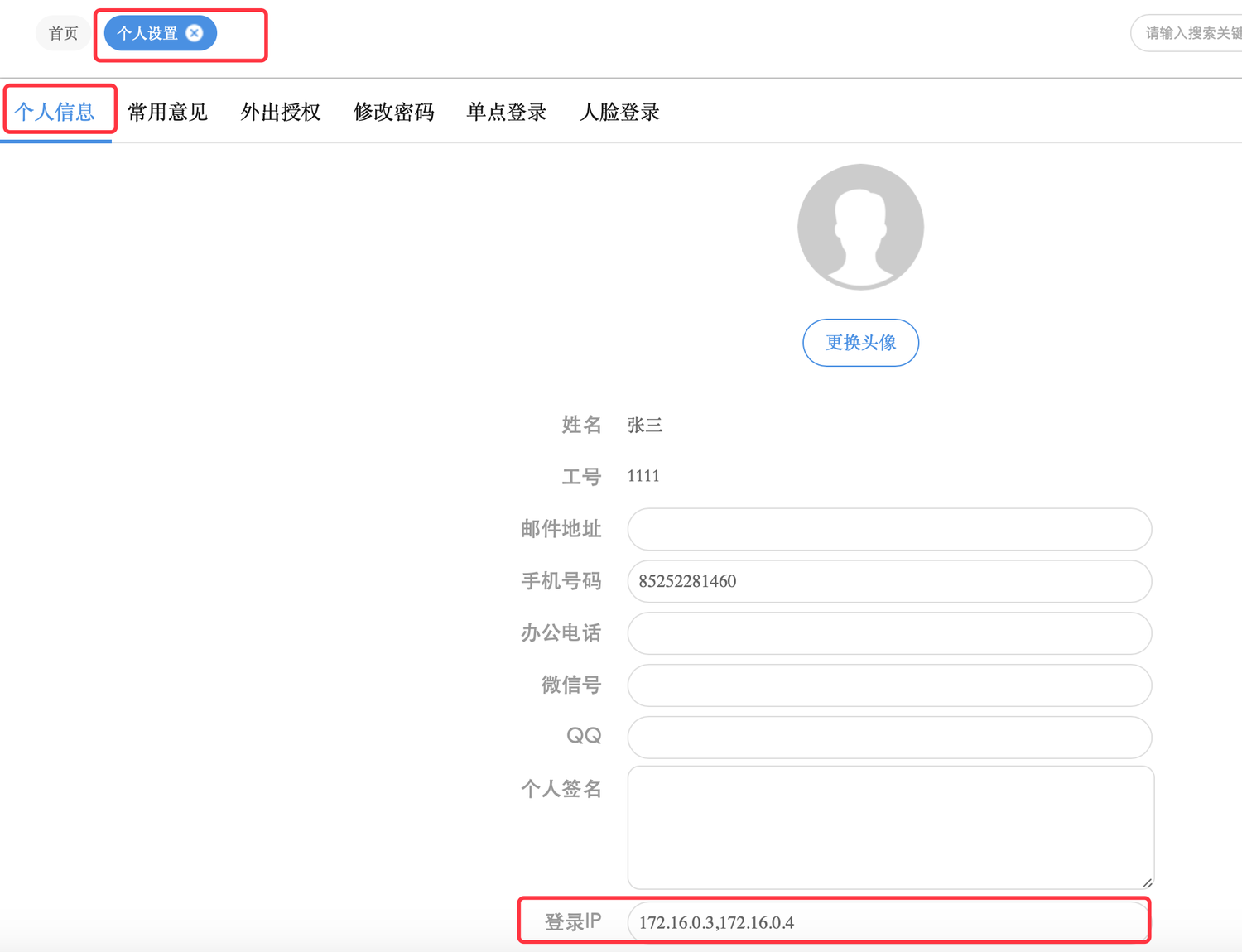
O2OA(翱途)开发平台系统安全-用户登录IP限制
O2OA(翱途)开发平台[下称O2OA开发平台或者O2OA]支持对指定的用户设置可以连接的客户端计算机的IP地址,以避免用户在不安全的环境下访问系统。本篇主要介绍如何开启O2OA用户登录IP限制。 一、先决条件: 1、O2Server服务器正常运行,系统安装部…...
DirectShowPlayerService::doSetUrlSource: Unresolved error code 0x800c000d
报出这个问题,应该是对给的url解析不正确,我给的是rtsp的视频流地址,应该是对该格式解析异常。 所以参考两篇文: QT无法播放视频:报错:DirectShowPlayerService::doRender: Unresolved error code 0x8004…...

【测试流程及规范】8000字超详细完整版
前言: 首先注明该文由本人原创,转载时需注明出处;团队背景:测试团队加上我一共5名,Java开发10多位,前端3位,产品4位,还有架构工程师、运维等;公司IT团队开发的系统仅供内…...

第十四届蓝桥杯省赛真题 Java C 组【原卷】
文章目录 发现宝藏【考生须知】试题 A \mathrm{A} A : 求和试题 B: 分糖果试题 C: 三国游戏试题 D : \mathrm{D}: D: 平均试题 E \mathrm{E} E : 填充试题 F : \mathrm{F}: F: 棋盘试题 G: 子矩阵试题 H: 公因数匹配试题 I: 异或和之差试题 J : \mathrm{J}: J: 太阳 发现宝…...

v-model 粗略解析
v-model 粗略解析 v-model是什么? 双向数据绑定,可以从data流向页面,也可以从页面流向data通常用于表单收集,v-model 默认绑定 value 值书写形式: v-model:value"" 或 v-model v-model原理是什么…...

【vue elementUI】修改el-dropdown样式
实现效果如下: 代码如下: <el-dropdown trigger"click" command"handleCommand" active-text-color"#606266"><span class"product-card">{{getCategoryName(categoryId)}}</span><el-dro…...
6语言交易所/多语言交易所php源码/微盘PHP源码
6语言交易所PHP源码,简单测试了一下,功能基本都是正常的。 由于是在本地测试的运行环境的问题,K线接口有点问题,应该在正式环境下是OK的。 源码下载地址:6语言交易所/多语言交易所php源码/微盘PHP源码.zip 程序截图…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...

PostgreSQL 对 IPv6 的支持情况
PostgreSQL 对 IPv6 的支持情况 PostgreSQL 全面支持 IPv6 网络协议,包括连接、存储和操作 IPv6 地址。以下是详细说明: 一、网络连接支持 1. 监听 IPv6 连接 在 postgresql.conf 中配置: listen_addresses 0.0.0.0,:: # 监听所有IPv4…...
