电子技术——晶体管尺寸
电子技术——晶体管尺寸
在本节我们介绍关于IC设计的一个重要的参数晶体管尺寸(例如长度和长宽比)。我们首先考虑MOS反相器。
反相器尺寸
为了说明 (W/L)(W/L)(W/L) 的尺寸大小以及 (W/L)p(W/L)_p(W/L)p 和 (W/L)n(W/L)_n(W/L)n 的比例问题对于MOS的性能问题。
- 为了缩小尺寸,所有沟道的长度在工艺允许的情况下应该设计成一样以来缩小IC尺寸。
- 对于给定的反相器,如果我们希望严格减小最小面积,则 (W/L)n(W/L)_n(W/L)n 通常选择为 1 到 1.5 。对于 (W/L)p(W/L)_p(W/L)p 的选择相对于 (W/L)n(W/L)_n(W/L)n 会影响噪声容限和 tPLHt_{PLH}tPLH 。设计师应该优化 QPQ_PQP 和 QNQ_NQN 的匹配问题,我们之前知道越好的匹配就会造成IC硅面积的浪费而且还会增加有效的容抗 CCC ,所以尽管 tPLH=tPHLt_{PLH} = t_{PHL}tPLH=tPHL 此时两个值均大于没有完美匹配的情况。因此选择 (W/L)p=(W/L)n(W/L)_p = (W/L)_n(W/L)p=(W/L)n 是一种选择,但是 (W/L)p=2(W/L)n(W/L)_p = 2(W/L)_n(W/L)p=2(W/L)n 通常是在权衡利弊的情况下的一种更优的选择。
- 解决完 (W/L)p(W/L)_p(W/L)p 和 (W/L)n(W/L)_n(W/L)n 的比例匹配问题,我们需要选择 (W/L)n(W/L)_n(W/L)n 来减小 tPt_PtP 从而提高数字系统的响应时间。增加 (W/L)n(W/L)_n(W/L)n 就会增加MOS的面积,进而导致电容 CCC 的增加。为了更精确的说明,我们将 CCC 表示为 C=Cint+CextC = C_{int} + C_{ext}C=Cint+Cext 其中 CintC_{int}Cint 是MOS管的内部电容,而 CextC_{ext}Cext 是MOS的外部电容,包括线间电容和负载输入容抗。
增加MOS的长宽比 W/LW/LW/L 为最小尺寸反相器的 SSS 倍,会导致:
C=SCint0+CextC = SC_{int0} + C_{ext} C=SCint0+Cext
这里 Cint0C_{int0}Cint0 是最小尺寸反相器的内部电容。
现在,若我们使用RC方法计算 tPt_PtP ,等效的电阻为:
Req=12(RN+RP)R_{eq} = \frac{1}{2}(R_N + R_P) Req=21(RN+RP)
那么:
tP=0.69ReqCt_P = 0.69R_{eq}C tP=0.69ReqC
若我们定义最小尺寸反相器的等效电阻为 Req0R_{eq0}Req0 ,增加MOS的长宽比 W/LW/LW/L 为最小尺寸反相器的 SSS 倍会导致:
Req=Req0/SR_{eq} = R_{eq0} / S Req=Req0/S
带入所有的表达式可以得到:
tP=0.69(Req0S)(SCint0+Cext)=0.69(Req0Cint0+1SReq0Cext)t_P = 0.69(\frac{R_{eq0}}{S}) (SC_{int0} + C_{ext}) = 0.69(R_{eq0}C_{int0} + \frac{1}{S} R_{eq0}C_{ext}) tP=0.69(SReq0)(SCint0+Cext)=0.69(Req0Cint0+S1Req0Cext)
这说明放大比例 SSS 并不会影响内部电容对于 tPt_PtP 的影响,然而,会降低外部电容的分量值。我们可以使用上式来选择一个合适的 SSS 来将 tPt_PtP 保持在最小值,同时要注意增加 SSS 会增加MOS的硅面积。
CMOS逻辑门中的晶体管尺寸
当决定使用CMOS电路的时候,唯一的重要的事情就是决定所有器件的 W/LW/LW/L 比例。最好情况下,我们必须让CMOS逻辑门电路的电流驱动能力必须等于相同的反相器的电流驱动能力。对于基本反相器,我们记 (W/L)n=n(W/L)_n = n(W/L)n=n 并且 (W/L)p=p(W/L)_p = p(W/L)p=p ,这里 n=1≃1.5n = 1 \simeq 1.5n=1≃1.5 ,对于匹配设计 p=(μn/μp)np = (\mu_n/\mu_p) np=(μn/μp)n 通常 p=2np = 2np=2n 对于最小尺寸设计 p=np = np=n 。因此,我们在设计PDN的时候,我们必须选择每一个MOS的长宽比让其PDN的泄放电流能力至少等于一个 W/L=nW/L = nW/L=n 的NMOS的泄放电流能力。同样的对于PUN来说,我们必须选择每一个MOS的长宽比让其PUN的提供电流能力至少等于一个 W/L=pW/L = pW/L=p 的PMOS的提供电流能力。这保证了逻辑门电路延迟的最坏情况——等同于基本反相器。
基于上述的讨论,我们必须强调“最坏情况”是什么。这意味着,我们在选择晶体管尺寸的时候,我们需要找到一种输入的组合方式使得最低输出电流等于基本反相器的电流。在我们讨论具体的例子之前,我们首先要解决如何决定多个MOS管组合逻辑门电路的电流的驱动能力,也就是找到等价单个MOS W/LW/LW/L 的值。首先我们考虑MOS串联和并联时候的情况。
基于 RonR_{on}Ron 与 W/LW/LW/L 反比的事实,若多个MOS管串联,每个MOS的宽长比分别为 (W/L)1,(W/L)2,…(W/L)_1,(W/L)_2,\ldots(W/L)1,(W/L)2,… 等价的电阻为:
Rseries=RN1+RN2+…=const(W/L)1+const(W/L)2+…=const[1(W/L)1+1(W/L)2+…]=const(W/L)eqR_{series} = R_{N1} + R_{N2} + \ldots = \frac{const}{(W/L)_1} + \frac{const}{(W/L)_2} + \ldots = const[\frac{1}{(W/L)_1} + \frac{1}{(W/L)_2} + \ldots] = \frac{const}{(W/L)_{eq}} Rseries=RN1+RN2+…=(W/L)1const+(W/L)2const+…=const[(W/L)11+(W/L)21+…]=(W/L)eqconst
那么等价的长宽比为:
(W/L)eq=11(W/L)1+1(W/L)2+…(W/L)_{eq} = \frac{1}{\frac{1}{(W/L)_1} + \frac{1}{(W/L)_2} + \ldots} (W/L)eq=(W/L)11+(W/L)21+…1
同样的方法,能够导出并联时候的情况:
(W/L)eq=(W/L)1+(W/L)2+…(W/L)_{eq} = (W/L)_1 + (W/L)_2 + \ldots (W/L)eq=(W/L)1+(W/L)2+…
现在,考虑下图的一个四变量输入的或非门:
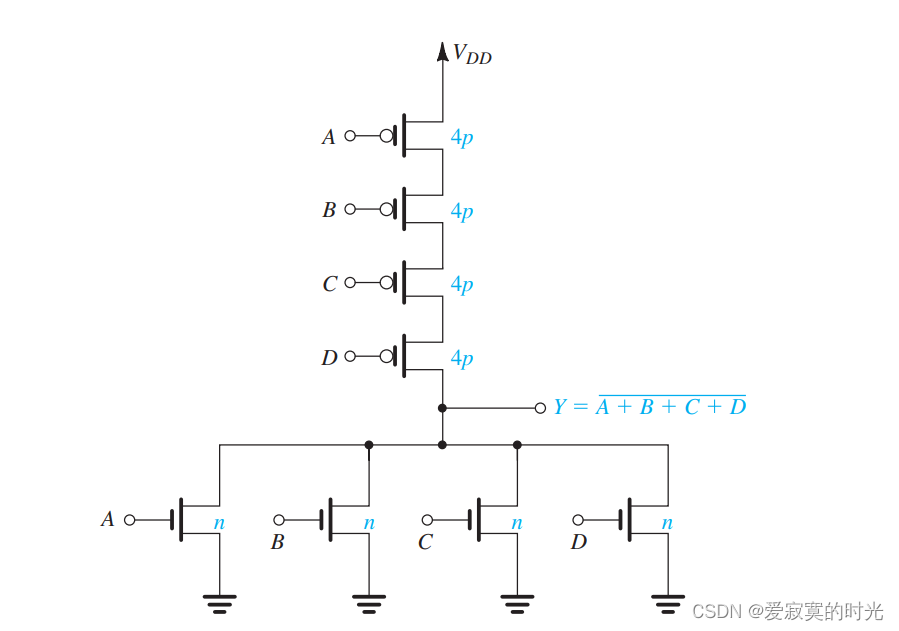
其中对于PDN来说,最坏的情况(最小电流)是四个NMOS只有一个导通,因此,我们对于每一个NMOS都选择 W/L=nW/L = nW/L=n 即可。对于PUN来说最坏的情况(也是唯一的情况)是四个PMOS均导通,根据串联MOS公式,我们让每个PMOS的 W/L=4pW/L = 4pW/L=4p 即可。
另外一个例子是四变量输入的与非门,如图:
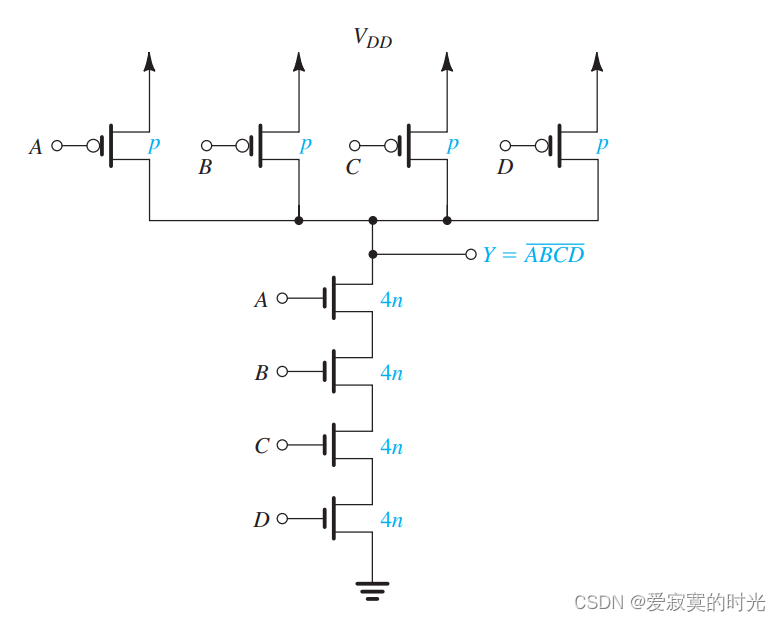
需要注意的是,通常 ppp 是 nnn 的2到3倍,因此或非门的体积要大于与非门的体积。基于此原因,设计师更愿意使用NAND来实现组合逻辑。
扇入扇出效应与传播延迟
每一个CMOS们电路的每一个输入变量都需要提供给两个晶体管,一个NMOS和一个PMOS。相比于另外一种只需要一种输入链接到一个晶体管的MOS逻辑门电路来说,例如伪NMOS逻辑门电路,额外的晶体管不仅增加了芯片的面积,而且还增加总有效阻抗从而增加了传播延迟。增加MOS的宽长比可以在一定程度上补偿这种传播延迟。特别的,通过增大元件的尺寸,我们可以保留电流驱动能力,然而却增加了总有效容抗。因此 tPt_PtP 仍然会受到扇入数的影响,扇入数指的实际的接入晶体管数量,例如NAND的扇入数是4。如果需要更多的输入变量,明智的电路设计者会通过巧妙的变换或者设计让输入变量的个数不超过4个。这通常意味着需要增加联级的数量,这同样会增加传播延迟。然而,相比之下,这种方法的传播延迟增加总比之前未优化的情况要小。
同样的,对于扇出数来说,其直接关系到负载的容抗,因此扇出数越大,则负载的容抗越大,传播延迟越大。
因此尽管CMOS有许多优点,当扇入和扇出数增加的时候,同样会受到电路复杂性的影响,导致芯片面积和传播延迟的增加。
驱动大电容
在一些特别的CMOS电路中,需要驱动较大的容性负载。例如,在IC中较长的走线,或是需要通过片外PCB走线的信号,此时的容抗要比普通情况下的容抗大上百倍。
我们需要一种在可以忍受的传播延迟下驱动大容抗的方法。下图展示了一个标准反相器驱动电容 CLC_LCL 的演示图:
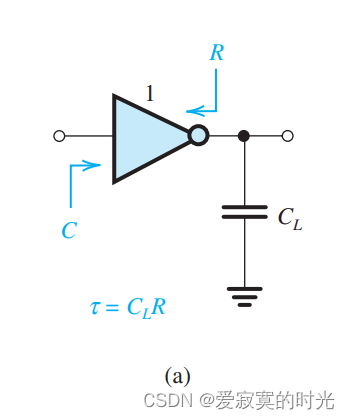
上面的模型,我们简单的总结为从输入端看过去容值为 CCC 等效电容为 RRR 的CR模型,因为 CLC_LCL 为负载容抗,根据估算:
tP=τ=CLRt_P = \tau = C_LR tP=τ=CLR
延迟将会非常大。
一种解决方法是,放大反相器的体积,如图:
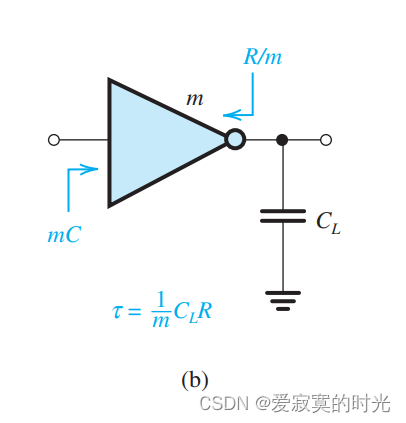
这里的反相器是参考反相器的 mmm 倍,此时输出电阻将会是 R/mR/mR/m ,此时的传播延迟为:
τ=CL(R/m)\tau = C_L(R/m) τ=CL(R/m)
传播延迟将会降低 mmm 倍,但是这并不是一个方法。观察到输入的容抗变成了原来的 mmm 倍,这需要一个更大的反相器来驱动他,并没从根本上解决问题,而是把负担交给了其他反相器。
但是,这种方法给我们了一种解决问题的思路,即使用联级反相器,如图:
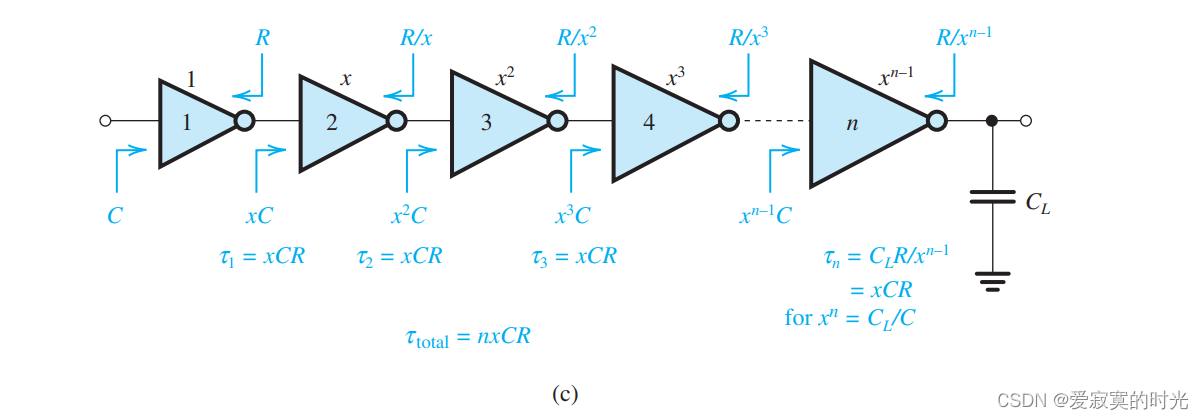
观察上图,我们发现反相器的尺寸成等比数列,我们发现每一级之间的传播延迟都为:
τ=xCR\tau = xCR τ=xCR
特别的,可以证明当满足:
τn≡CL(Rxn−1)=xCR\tau_n \equiv C_L(\frac{R}{x^{n-1}}) = xCR τn≡CL(xn−1R)=xCR
的时候,也就是:
xn=CLCx^n = \frac{C_L}{C} xn=CCL
整体延迟最小为:
tP=τtotal=nxCRt_P = \tau_{total} = nxCR tP=τtotal=nxCR
问题是如何选定 xxx 和 nnn 。在数学中可以证明,当 x=e≃2.718x = e \simeq 2.718x=e≃2.718 的时候,传播延迟最小。实际上,在2.5-4之间都可以提升性能。
相关文章:

电子技术——晶体管尺寸
电子技术——晶体管尺寸 在本节我们介绍关于IC设计的一个重要的参数晶体管尺寸(例如长度和长宽比)。我们首先考虑MOS反相器。 反相器尺寸 为了说明 (W/L)(W/L)(W/L) 的尺寸大小以及 (W/L)p(W/L)_p(W/L)p 和 (W/L)n(W/L)_n(W/L)n 的比例问题对于MO…...

Tuxera NTFS2023MacOS读写软件功能介绍使用
当我们遇到磁盘不能正常使用的情况时本能的会以为是磁盘损坏了,但某些情况下却并非如此。对于mac操作系统来说,软件无法使用设备无法正常读写似乎是很常见的事,毕竟现在的mac电脑对PC机上的产品无法完全适应使用,经常会存在兼容方…...

2022年数维杯国际大学生数学建模挑战赛A题自动地震地平线跟踪解题全过程论文及程序
2022年数维杯国际大学生数学建模挑战赛 A题 自动地震地平线跟踪 原题再现: 随着我国经济社会发展,地质工作的重要性也日益提高。地震资料解释是地震勘探工程的一个重要阶段,可以明确油气勘探的地下构造特征,为油气勘探提供良好和…...

推荐系统[八]:推荐系统常遇到问题和解决方案[物品冷启动问题、多目标平衡问题、数据实时性问题等]
相关文章推荐: 推荐系统[一]:超详细知识介绍,一份完整的入门指南,解答推荐系统相关算法流程、衡量指标和应用,以及如何使用jieba分词库进行相似推荐,业界广告推荐技术最新进展 推荐系统[二]:召回算法超详细讲解[召回模型演化过程、召回模型主流常见算法(DeepMF/TDM/Ai…...

shutil.copyfile PermissionError: [Errno 13] Permission denied
File "G:/od15/调试/翻译文件更换/更新翻译po文件.py", line 42, in <module> shutil.copyfile(gxpath,dir_file_path) File "E:\odsoft\python\lib\shutil.py", line 120, in copyfile with open(src, rb) as fsrc: PermissionError: [Er…...
07react+echart,大屏代码开发
react框架引入第三方插件原链接gitHub:GitHub - hustcc/echarts-for-react: ⛳ Apache ECharts components for React wrapper. 一个简单的 Apache echarts 的 React 封装。import ReactECharts from echarts-for-react;import * as echarts from echarts;一、软件简介echarts-…...
)
【数据库原理复习】ch2 SQL语句(主要基于sql server)
这里写目录标题基本知识常用基本数据类型字符型数据类型二进制数据类型日期类型数字类型约束条件表SQL语句创建语句修改基本表 & 删除基本表数据查询基本知识 常用基本数据类型 字符型数据类型 名称大小说明char(n)占n个字节只能显示英文字符nchar(n)2n字节2字节额外开销…...

Cadence Allegro 导出Component Pin Report详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Component Pin Report作用3,Component Pin Report示例4,Component Pin Report导出方法4.1,方法14.2,方法2B站关注“硬小二”浏览更多演示视频 1,概述...

PAT甲级 1110 Complete Binary Tree
题目链接 PAT甲级 1110 Complete Binary Tree 思路 第一次的写法不是很好。 对于这种完全二叉树的层序遍历,比较烦人的就是空孩子使得处理很麻烦。 思来想去还是把空位置也入队比较好。 这样的话,访问到空指针的时机被推迟了一个level 而完全二叉树的…...
【JavaSE】逻辑控制语句
文章目录一. 顺序结构二. 分支结构1. if 语句2. switch 语句3、循环结构3.1 while 循环3.2 do while 循环3.3 for 循环3.4 break 和 continue三. 输入输出1. 输出到控制台2. 从键盘输入一. 顺序结构 顺序结构比较简单,即程序按照代码书写的顺序一行一行执行下去。 …...

Motionbuilder系统文件说明
安装路径 Motionbuilder 默认的安装路径在 C:\Program Files\Autodesk\MotionBuilder\ 用户数据(user data) 位于安装路径下的 bin\config 非管理员用户的配置文件路径 Motionbuilder会将配置文件备份到 \Users[user]\AppData\Local\Autodesk[MotionBuilder] 当用户第一次打开…...
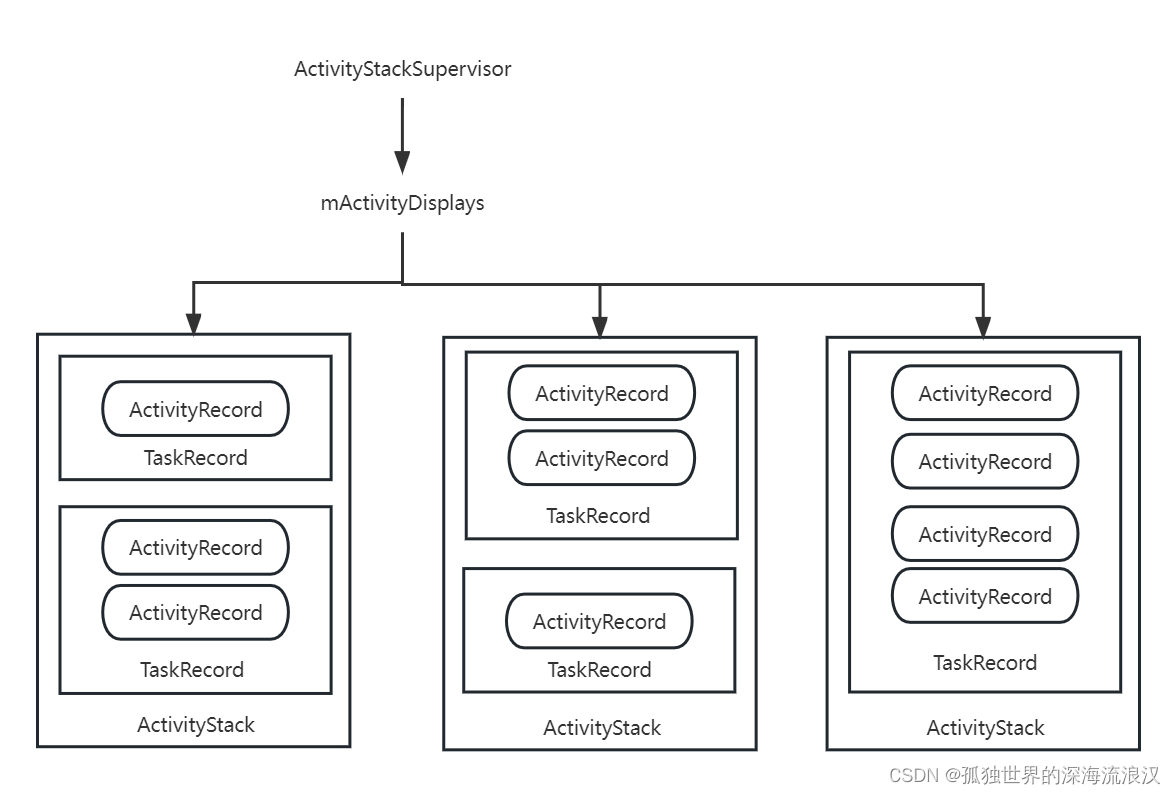
【我的Android开发】AMS中Activity栈管理
概述 Activity栈管理是AMS的另一个重要功能,栈管理又和Activity的启动模式和startActivity时所设置的Flag息息相关,Activity栈管理的主要处理逻辑是在ActivityStarter#startActivityUnchecked方法中,本文也会围绕着这个方法进进出出…...

C++源程序的构成————学习笔记
以下内容为,在学校上课时的课堂总结,偶尔我也会扩展一些内容内容仅供参考,欢迎大佬的指正简单的C程序#include <iostream> using namespace std;int main() {int x0;int y 0;cout << "请输入x,y的值"<<endl;cin…...

Spark Catalyst
Spark Catalyst逻辑计划逻辑计划解析逻辑计划优化Catalyst 规则优化过程物理计划Spark PlanJoinSelection生成 Physical PlanEnsureRequirementsSpark SQL 端到端的优化流程: Catalyst 优化器 : 包含逻辑优化/物理优化Tungsten : Spark SQL的优化过程 : 逻辑计划 …...

element 远程搜索下拉加载
created() { this.getList(); this.getGroupList(); }, directives: { /** 下拉框懒加载 */ “el-select-loadmore”: { bind(el, binding) { const SELECTWRAP_DOM el.querySelector( “.el-select-dropdown .el-select-dropdown__wrap” ); SELECTWRAP_DOM.addEventListener…...

空间复杂度与顺序表的具体实现操作(1)
最近更新的少,主要是因为参加了ACM竞赛空间复杂度空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量…...

【springmvc】Rest ful风格
RESTful 1、RESTful简介 REST:Representational State Transfer,表现层资源状态转移。 a>资源 资源是一种看待服务器的方式,即,将服务器看作是由很多离散的资源组成。每个资源是服务器上一个可命名的抽象概念。因为资源是一…...
)
华为OD机试真题Python实现【用户调度】真题+解题思路+代码(20222023)
用户调度 题目 在通信系统中有一个常见的问题是对用户进行不同策略的调度,会得到不同系统消耗的性能。 假设由N个待串行用户,每个用户可以使用A/B/C三种不同的调度策略。 不同的策略会消耗不同的系统资源,请你根据如下规则进行用户调度,并返回总的消耗资源数。 规则是: …...

JavaSE学习笔记总结day19
今日内容 二、线程安全的集合 三、死锁 四、线程通信 五、生产者消费者 六、线程池 零、 复习昨日 创建线程的几种方式 1) 继承 2) 实现Runnable 3) callable接口 Future接口 4) 线程池 启动线程的方法 start() 线程的几种状态 什么是线程不安全 setName getName Thread.curr…...
FreeSql使用
目的: 1.方库分表 2.主从分离 3.分布式事务 过程: 官网:指南 | FreeSql 官方文档 1.Startup.cs 添加配置(本地数据库MySql) ConfigureServices: Func<IServiceProvider, IFreeSql> fsql r >{IFreeSql …...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
