【数据结构与算法】:非递归实现快速排序、归并排序

🔥个人主页: Quitecoder
🔥专栏:数据结构与算法

上篇文章我们详细讲解了递归版本的快速排序,本篇我们来探究非递归实现快速排序和归并排序
目录
- 1.非递归实现快速排序
- 1.1 提取单趟排序
- 1.2 用栈实现的具体思路
- 1.3 代码实现
- 2.归并排序
1.非递归实现快速排序
快速排序的非递归实现主要依赖于栈(stack)来模拟递归过程中的函数调用栈。递归版本的快速排序通过递归调用自身来处理子数组,而非递归版本则通过手动管理一个栈来跟踪接下来需要排序的子数组的边界
那么怎样通过栈来实现排序的过程呢?
思路如下:
使用栈实现快速排序是对递归版本的模拟。在递归的快速排序中,函数调用栈隐式地保存了每次递归调用的状态。但是在非递归的实现中,你需要显式地使用一个辅助栈来保存子数组的边界
以下是具体步骤和栈的操作过程:
-
初始化辅助栈:
创建一个空栈。栈用于保存每个待排序子数组的起始索引(begin)和结束索引(end)。 -
开始排序:
将整个数组的起始和结束索引作为一对入栈。这对应于最初的排序问题。 -
迭代处理:
在栈非空时,重复下面的步骤:- 弹出一对索引(即栈顶元素)来指定当前要处理的子数组。
- 选择子数组的一个元素作为枢轴(pivot)进行分区(可以是第一个元素,也可以通过其他方法选择,下面我们还是用三数取中)。
- 进行分区操作,这会将子数组划分为比枢轴小的左侧部分和比枢轴大的右侧部分,同时确定枢轴元素的最终位置。
-
处理子数组:
分区操作完成后,如果枢轴元素左侧的子数组(如果存在)有超过一个元素,则将其起始和结束索引作为一对入栈。同样,如果右侧的子数组(如果存在)也有超过一个元素,也将其索引入栈 -
循环:
继续迭代该过程,直到栈为空,此时所有的子数组都已经被正确排序。
所以主要思路就两个:
- 分区
- 单趟排序
1.1 提取单趟排序
我们上篇文章讲到递归排序的多种方法,这里我们可以取其中的一种提取出单趟排序:
int Getmidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else{if (a[midi] > a[end])return midi;else if (a[end] < a[begin])return end;elsereturn begin;}
}
void QuickSortHole(int* arr, int begin, int end) {if (begin >= end) {return;}int midi = Getmidi(arr, begin, end);Swap(&arr[midi], &arr[begin]);int key = arr[begin]; int left = begin;int right = end;while (left < right) {while (left < right && arr[right] >= key) {right--;}arr[left] = arr[right];while (left < right && arr[left] <= key) {left++;}arr[right] = arr[left];}arr[left] = key; QuickSortHole(arr, begin, left - 1);QuickSortHole(arr, left + 1, end);
}
接下来完成单趟排序函数:
int singlePassQuickSort(int* arr, int begin, int end)
{if (begin >= end) {return;}// 选择枢轴元素int midi = Getmidi(arr, begin, end);Swap(&arr[midi], &arr[begin]);int key = arr[begin]; // 挖第一个坑int left = begin; // 初始化左指针int right = end; // 初始化右指针// 进行分区操作while (left < right) {// 从右向左找小于key的元素,放到左边的坑中while (left < right && arr[right] >= key) {right--;}arr[left] = arr[right];// 从左向右找大于key的元素,放到右边的坑中while (left < right && arr[left] <= key) {left++;}arr[right] = arr[left];}// 将枢轴元素放入最后的坑中arr[left] = key;// 函数可以返回枢轴元素的位置,若需要进一步的迭代过程return left;
}
1.2 用栈实现的具体思路
以下面这串数组为例:
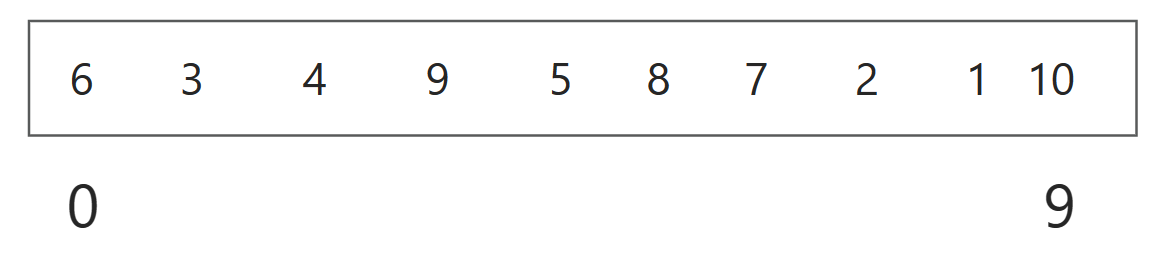
首先建立一个栈,将整个数组的起始和结束索引作为一对入栈
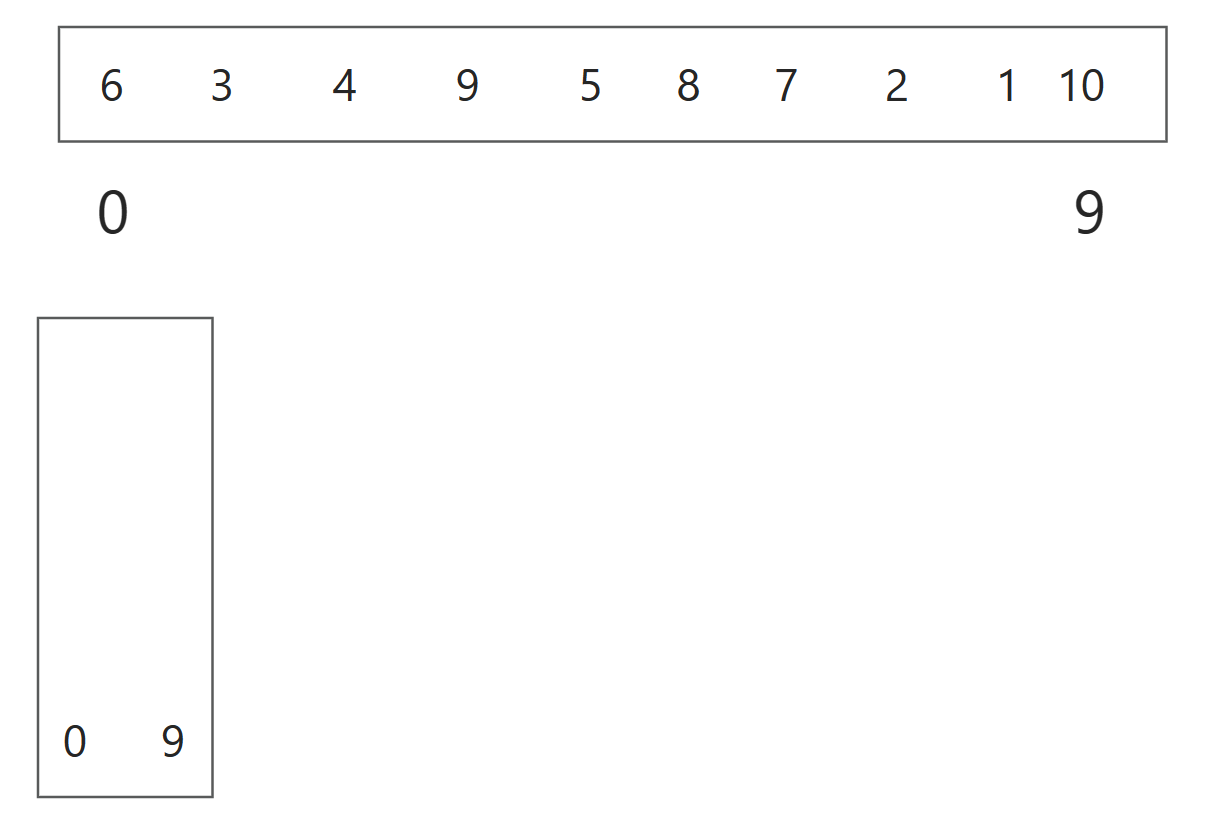
弹出一对索引(即栈顶元素)来指定当前要处理的子数组:这里即弹出0 9索引
找到枢轴6进行一次单趟排序:
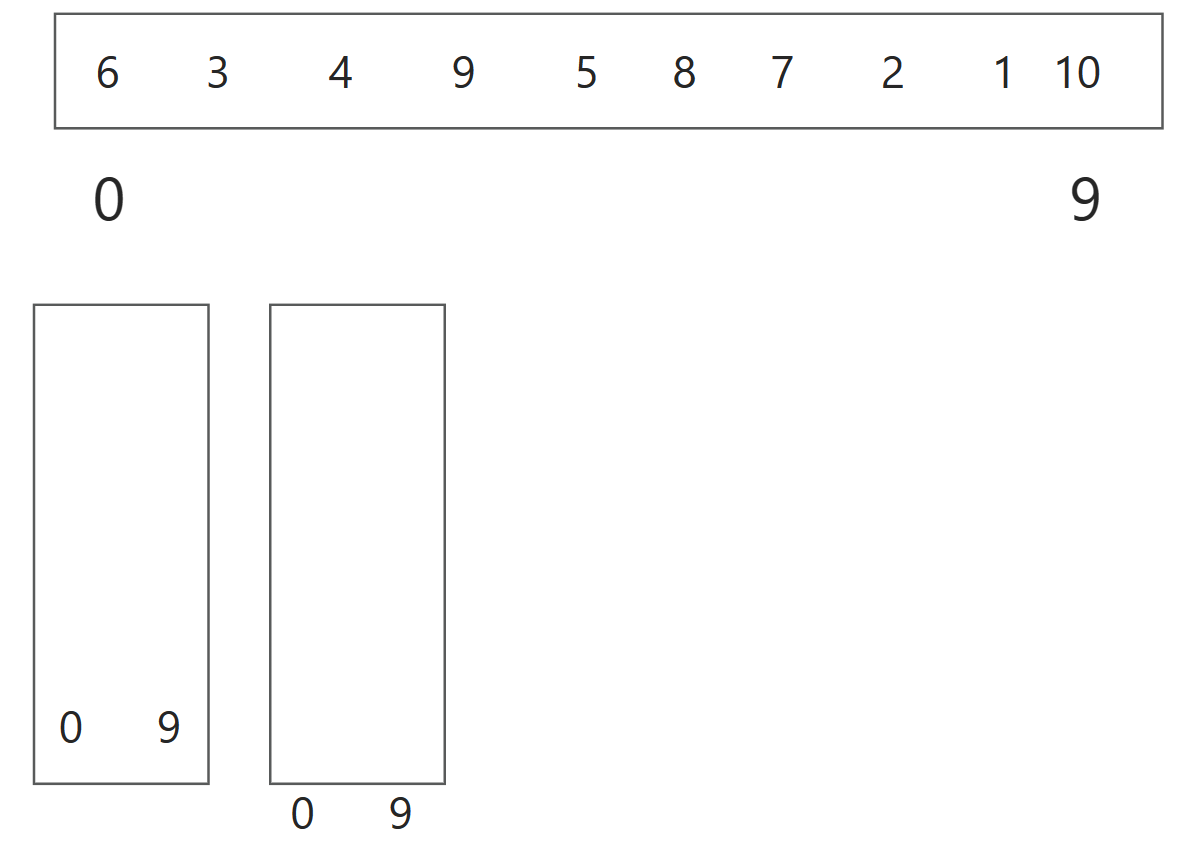
针对这个数组:
6 3 4 9 5 8 7 2 1 10
我们使用“三数取中”法选择枢轴。起始位置的元素为6,结束位置的元素为10,中间位置的元素为5。在这三个元素中,6为中间大小的值,因此选择6作为枢轴。因为枢轴已经在第一个位置,我们可以直接开始单趟排序。
现在,开始单趟排序:
- 枢轴值为
6。 - 从右向左扫描,找到第一个小于
6的数1。 - 从左向右扫描,找到第一个大于
6的数9。 - 交换这两个元素。
- 继续进行上述步骤,直到左右指针相遇。
经过单趟排序后:
6 3 4 1 5 2 7 8 9 10
接下来需要将枢轴6放置到合适的位置。我们知道,最终左指针和右指针会停在第一个大于或等于枢轴值6的位置。在这个例子中,左右指针会停在7上。现在我们将6与左指针指向的位置的数交换:
5 3 4 1 2 6 7 8 9 10
现在枢轴值6处于正确的位置,其左侧所有的元素都小于或等于6,右侧所有的元素都大于或等于6。
分区操作完成后,如果枢轴元素左侧的子数组(如果存在)有超过一个元素,则将其起始和结束索引作为一对入栈。同样,如果右侧的子数组(如果存在)也有超过一个元素,也将其索引入栈
我们接下来完成这个入栈过程:让两个子数组的索引入栈
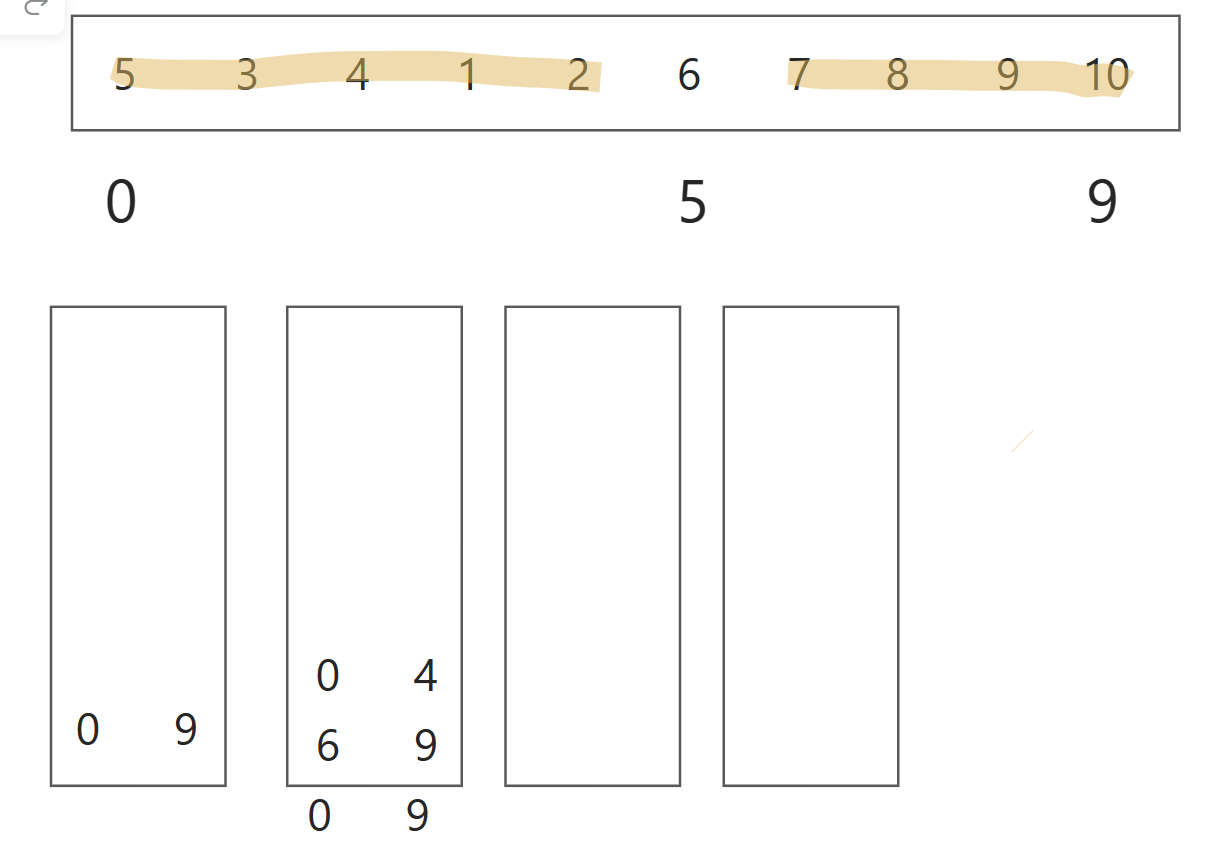
接着取0 4索引进行单趟排序并不断分区,分割的索引继续压栈,继续迭代该过程,直到栈为空,此时所有的子数组都已经被正确排序
1.3 代码实现
这里我们调用之前的栈的代码,基本声明如下:
typedef int STDataType;typedef struct Stack
{STDataType* a;int top;int capacity;
}ST; void StackInit(ST* ps);
// 入栈
void StackPush(ST* ps, STDataType x);
// 出栈
void StackPop(ST* ps);
// 获取栈顶元素
STDataType StackTop(ST* ps);
// 获取栈中有效元素个数
int StackSize(ST* ps);
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
bool StackEmpty(ST* ps);
// 销毁栈
void StackDestroy(ST* ps);
我们接下来完成排序代码,首先建栈,初始化,并完成第一个压栈过程:
ST s;
StackInit(&s);
StackPush(&s, end);
StackPush(&s, begin);
实现一次单趟排序:
int left = StackTop(&s);
StackPop(&s);int right = StackTop(&s);
StackPop(&s);int keyi = singlePassQuickSort(a, left, right);
注意这里我们先压入end,那么我们先出的就是begin,用left首先获取begin,再pop掉获取end
接着判断keyi左右是否还有子数组
if (left < keyi - 1)
{StackPush(&s, keyi - 1);StackPush(&s, left);
}
if (keyi + 1<right)
{StackPush(&s, right);StackPush(&s, keyi+1);
}
将此过程不断循环即为整个过程,总代码如下:
void Quicksortst(int* a, int begin, int end)
{ST s;StackInit(&s);StackPush(&s, end);StackPush(&s, begin);while (!StackEmpty(&s)){int left = StackTop(&s);StackPop(&s);int right = StackTop(&s);StackPop(&s);int keyi = singlePassQuickSort(a, left, right);if (left < keyi - 1){StackPush(&s, keyi - 1);StackPush(&s, left);}if (keyi + 1<right){StackPush(&s, right);StackPush(&s, keyi+1);}}StackDestroy(&s);
}
这里思想跟递归其实是差不多的,也是一次取一组进行排序,递归寻找每个区间
2.归并排序
假如我们已经有了两个已经排序好的数组,我们如何让他们并为一个有序的数组呢?
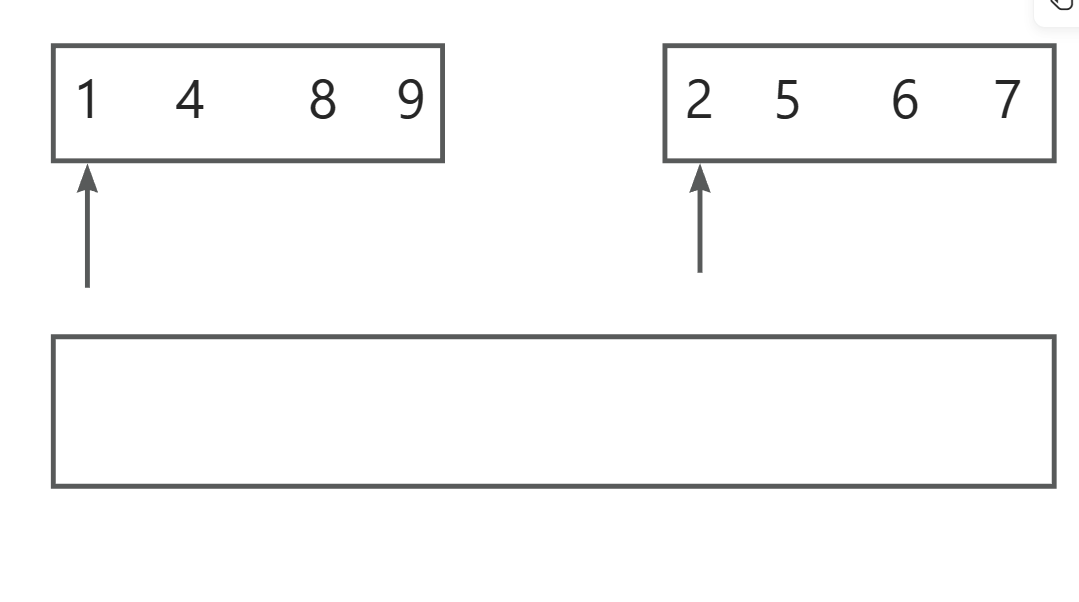
我们的做法就是用两个索引进行比较,然后插入一个新的数组完成排序,这就是归并排序的基础思路
那如果左右不是两个排序好的数组呢?
下面是归并排序的算法步骤:
-
递归分解数组:如果数组的长度大于1,首先将数组分解成两个部分。通常这是通过将数组从中间切分为大致相等的两个子数组
-
递归排序子数组:递归地对这两个子数组进行归并排序,直到每个子数组只包含一个元素或为空,这意味着它自然已经排序好
-
合并排序好的子数组:将两个排序好的子数组合并成一个排序好的数组。这通常通过设置两个指针分别指向两个子数组的开始,比较它们指向的元素,并将较小的元素放入一个新的数组中,然后移动指针。重复此过程,直到所有元素都被合并进新数组
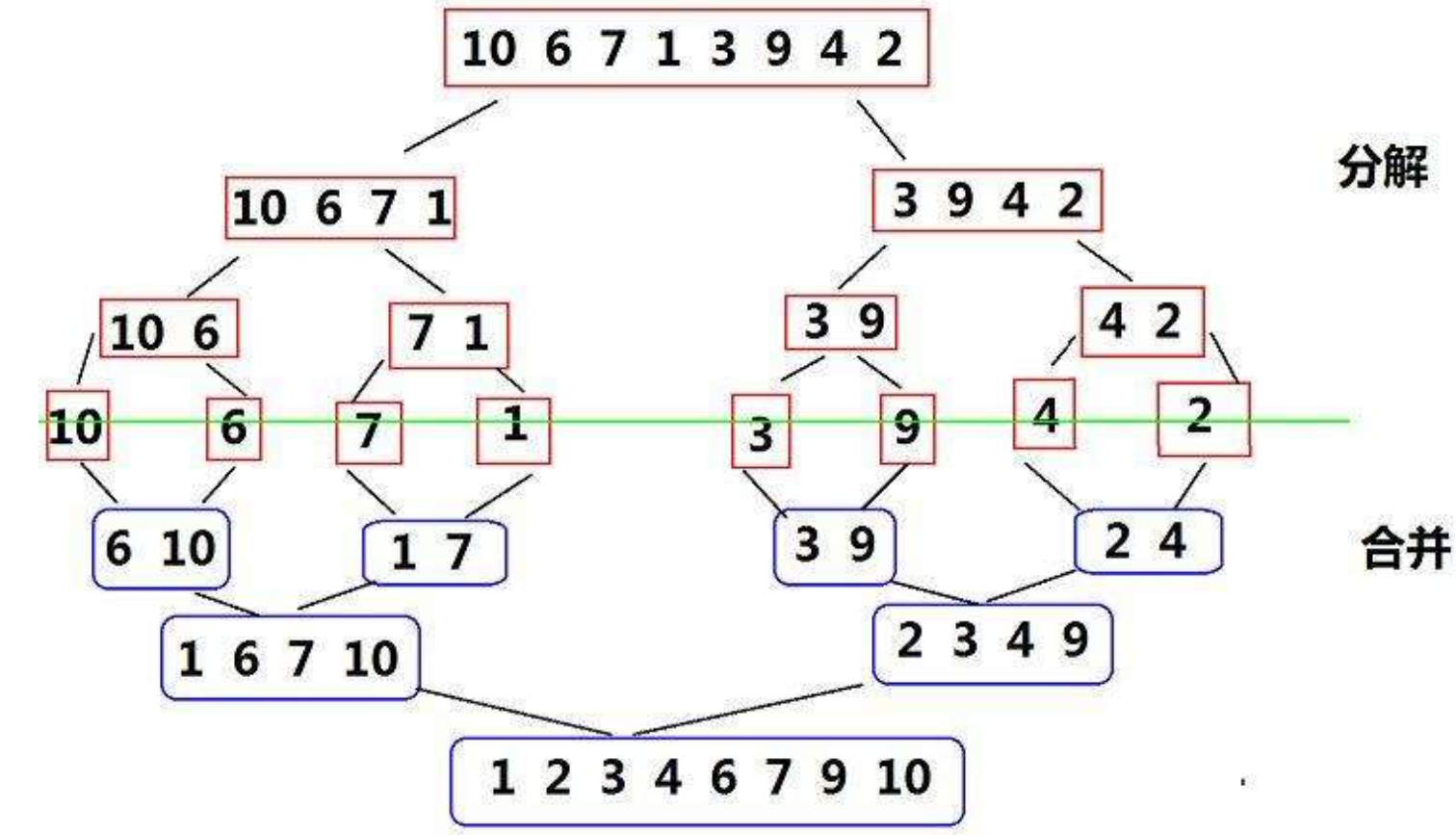
所以我们得需要递归来实现这一过程,首先声明函数并建造新的数组:
void MergeSort(int* a, int n)
{int* tmp =(int *) malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}free(tmp);
}
由于我们不能每次开辟一遍数组,我们这里就需要一个子函数来完成递归过程:
void _MergrSort(int* a, int begin, int end, int* tmp);
首先,不断递归将数组分解:
int mid = (begin + end) / 2;if (begin >= end)
{return;
}
_MergrSort(a, begin, mid, tmp);
_MergrSort(a, mid+1, end, tmp);
接着获取分解的两个数组的各自的首端到尾端的索引:
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
令要插入到数组tmp的起点为begin处:
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
接下来遍历两个数组,无论谁先走完都跳出循环
while (begin1 <= end1 && begin2 <= end2)
{if (a[begin1] < a[begin2]){tmp[i] = a[begin1];i++;begin1++;}else{tmp[i] = a[begin2];i++;begin2++;}
}
这时会有一方没有遍历完,按照顺序插入到新数组中即可
while (begin1 <= end1)
{tmp[i] = a[begin1];begin1++;i++;
}
while (begin2<= end2)
{tmp[i] = a[begin2];begin2++;i++;
}
插入到新数组后,我们拷贝到原数组中即完成了一次排序
memcpy(a+begin,tmp+begin,sizeof(int )*(end-begin+1));完整代码如下:
void _MergrSort(int* a, int begin, int end, int* tmp)
{int mid = (begin + end) / 2;if (begin >= end){return;}_MergrSort(a, begin, mid, tmp);_MergrSort(a, mid+1, end, tmp);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i] = a[begin1];i++;begin1++;}else{tmp[i] = a[begin2];i++;begin2++;}}while (begin1 <= end1){tmp[i] = a[begin1];begin1++;i++;}while (begin2<= end2){tmp[i] = a[begin2];begin2++;i++;}memcpy(a+begin,tmp+begin,sizeof(int )*(end-begin+1));
}
void MergeSort(int* a, int n)
{int* tmp =(int *) malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergrSort(a, 0, n - 1, tmp);free(tmp);
}
- 排序好的左半部分和右半部分接着被合并。为此,使用了两个游标
begin1和begin2,它们分别指向两个子数组的起始位置,然后比较两个子数组当前元素,将较小的元素拷贝到tmp数组中。这个过程继续直到两个子数组都被完全合并 - 在所有元素都被合并到tmp数组之后,使用memcpy将排序好的部分拷贝回原数组a。这个地方注意memcpy的第三个参数,它是
sizeof(int)*(end - begin + 1),表示拷贝的总大小,单位是字节 - begin和end变量在这里表示待排序和合并的数组部分的起止索引
本节内容到此结束!感谢大家阅读!
相关文章:

【数据结构与算法】:非递归实现快速排序、归并排序
🔥个人主页: Quitecoder 🔥专栏:数据结构与算法 上篇文章我们详细讲解了递归版本的快速排序,本篇我们来探究非递归实现快速排序和归并排序 目录 1.非递归实现快速排序1.1 提取单趟排序1.2 用栈实现的具体思路1.3 代码…...

2024-3-18-C++day6作业
1>思维导图 2>试编程 要求: 封装一个动物的基类,类中有私有成员:姓名,颜色,指针成员年纪 再封装一个狗这样类,共有继承于动物类,自己拓展的私有成员有:指针成员:腿的个数&a…...
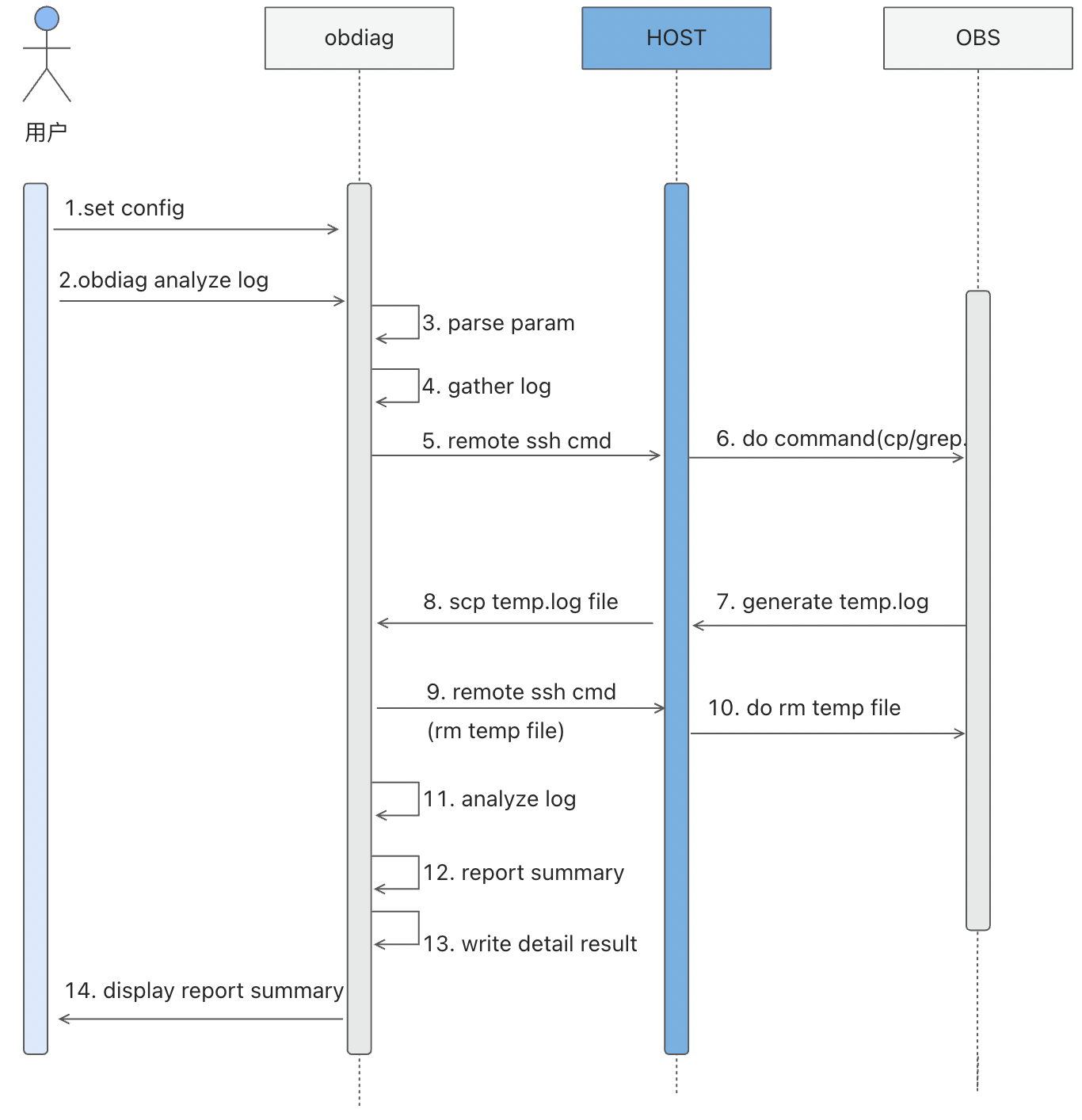
【OceanBase诊断调优】—— 敏捷诊断工具obdiag一键分析OB集群日志设计与实践
最近总结一些诊断OCeanBase的一些经验,出一个【OceanBase诊断调优】专题,也欢迎大家贡献自己的诊断OceanBase的方法。 1. 前言 obdiag定位为OceanBase敏捷诊断工具。1.2版本的obdiag支持诊断信息的一键收集,光有收集信息的能力,…...
python 调用redis创建查询key
部署redis apiVersion: apps/v1 # 描述api版本,默认都用这个 kind: Deployment # 资源类型,可以配置为pod,deployment,service,statefulset等等 metadata: # deployment相关的元数据,用于描述deployment的…...

归并排序思路
归并排序是一种经典的分治算法,其基本思路可以简述为以下几步: 分解:将待排序的数组递归地分解成较小的子数组,直到每个子数组只包含一个元素为止。这里采用分治的思想,将问题不断地划分为规模更小的子问题。 合并&am…...

【蓝桥杯选拔赛真题65】python输出三个字符 第十五届青少年组蓝桥杯python选拔赛真题 算法思维真题解析
目录 python输出3个字符 一、题目要求 1、编程实现 2、输入输出...
K8S日志收集方案-EFK部署
EFK架构工作流程 部署说明 ECK (Elastic Cloud on Kubernetes):2.7 Kubernetes:1.23.0 文件准备 crds.yaml 下载地址:https://download.elastic.co/downloads/eck/2.7.0/crds.yaml operator.yaml 下载地址:https://download.e…...
)
js基础语法大全(时间戳,uuid,字符串转json)
目录 一、获取时间戳二、获取uuid三、字符串转json格式 一、获取时间戳 var times Math.round(new Date().getTime()/1000).toString(); //获取 10位 时间戳 console.log(times);二、获取uuid function guid() {return xxxxxxxx-xxxx-4xxx-yxxx-xxxxxxxxxxxx.replace(/[xy]…...
uView LoadingIcon 加载动画
此组件为一个小动画,目前用在uView的loadMore加载更多等组件的正在加载状态场景。 #平台差异说明 App(vue)App(nvue)H5小程序√√√√ #基本使用 通过mode设定动画的类型,circle为圆圈的形状࿰…...
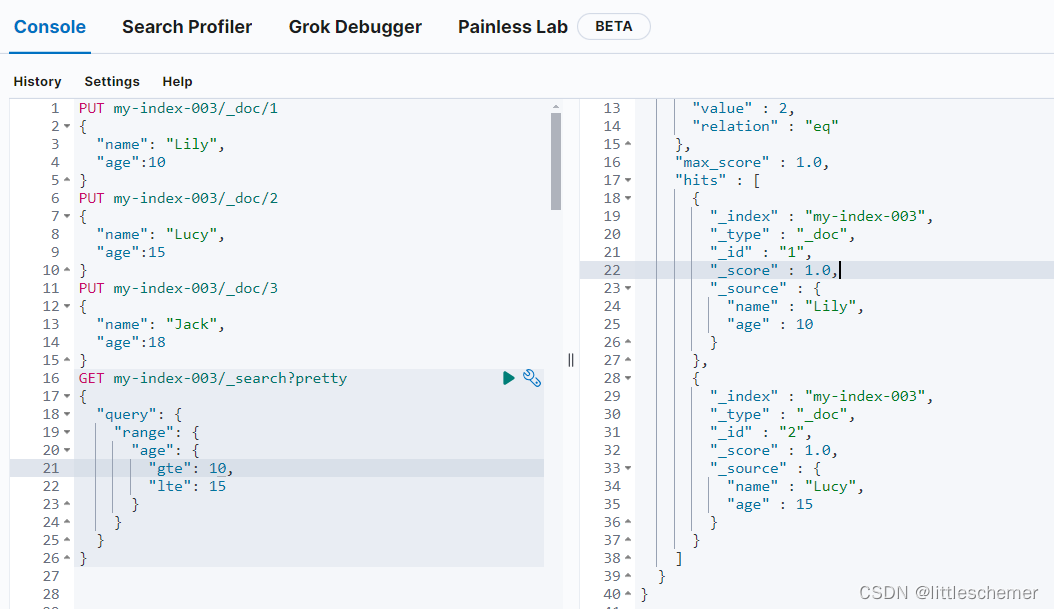
Elasticsearch使用Kibana进行基础操作
一、Restful接口 Elasticsearch通过RESTful接口提供与其进行交互的方式。在ES中,提供了功能丰富的RESTful API的操作,包括CRUD、创建索引、删除索引等操作。你可以用你最喜爱的 web 客户端访问 Elasticsearch 。事实上,你甚至可以使用 curl …...
“SRP模型+”多技术融合在生态环境脆弱性评价模型构建、时空格局演变分析与RSEI 指数的生态质量评价及拓展应用教程
原文链接:“SRP模型”多技术融合在生态环境脆弱性评价模型构建、时空格局演变分析与RSEI 指数的生态质量评价及拓展应用教程https://mp.weixin.qq.com/s?__bizMzUzNTczMDMxMg&mid2247597452&idx5&snf723d9e5858a269d00e15dbe2c7d3dc0&chksmfa823c6…...
【Windows 常用工具系列 15 -- VMWARE ubuntu 安装教程】
文章目录 安装教程镜像下载 工具安装 安装教程 安装教程参考链接:https://blog.csdn.net/Python_0011/article/details/131619864 https://linux.cn/article-15472-1.html 激活码 VMware 激活码连接:https://www.haozhuangji.com/xtjc/180037874.html…...
SpringSecurity(SpringBoot2.X版本实现)
资料来源于 SpringSecurity框架教程-Spring SecurityJWT实现项目级前端分离认证授权 侵权删 目录 介绍 快速开始 认证 认证流程 登录校验流程 SpringSecurity完整流程 认证流程详解 代码实现 准备工作 mysql mybatis-plus redis 统一返回类 核心代码 密码加密存…...

仿牛客项目Day8:社区核心功能2
显示评论 数据库 entity_type代表评论的目标类型,评论帖子和评论评论 entity_id代表评论的目标id,具体是哪个帖子/评论 targer_id代表评论指向哪个人 entity public class Comment {private int id;private int userId;private int entityType;priv…...
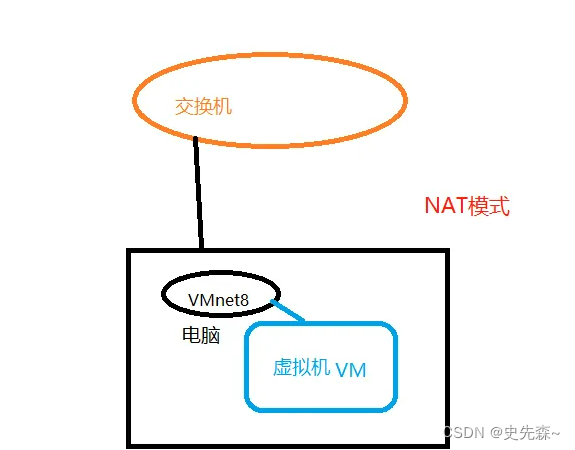
Vmware虚拟机配置虚拟网卡
背景 今天同事咨询了我一个关于虚拟机的问题,关于内网用Vmware安装的虚拟机,无法通过本机访问虚拟上的Jenkins的服务。 验证多次后发现有如下几方面问题。 Jenkins程序包和JDK版本不兼容(JDK1.8对应Jenkins不要超过2.3.57)虚…...

双向链表代码(带哨兵位循环/不带哨兵位不循环
以下代码全为本人所写,如有错误,很正常,还请指出, 目录 带哨兵位循环 test.c DLList.c DLList.h 不带哨兵位不循环 test.c DLList.c DLList.h 带哨兵位循环 test.c #define _CRT_SECURE_NO_WARNINGS#include"DLlist.h&…...

C语言自学笔记13----C语言指针与函数
C 语言指针与函数 在C语言编程中,也可以将地址作为参数传递给函数。 要在函数定义中接受这些地址,我们可以使用指针。这是因为指针用于存储地址。让我们举个实例: 示例:通过引用致电 #include <stdio.h> void swap(int n1, …...

每日五道java面试题之mybatis篇(一)
目录: 第一题. MyBatis是什么?第二题. ORM是什么?第三题. 为什么说Mybatis是半自动ORM映射工具?它与全自动的区别在哪里?第四题. 传统JDBC开发存在的问题第五题. JDBC编程有哪些不足之处,MyBatis是如何解决这些问题的…...

一文解读ISO26262安全标准:概念阶段
一文解读ISO26262安全标准:概念阶段 1 相关项定义2 安全生命周期启动3 危害分析和风险评估 HaRa4 功能安全概念 由上一篇文章知道,安全生命周期包含概念阶段、产品开发阶段、生产发布后续阶段。本文详细解读概念阶段要进行的安全活动。 本部分规定了车辆…...
微信小程序调用百度智能云API(菜品识别)
一、注册后生成应用列表创建应用 二、找到当前所需使用的api菜品识别文档 三、点链接看实例代码 这里需要使用到如下几个参数(如下),其他的参数可以不管 client_id : 就是创建应用后的API Keyclient_secret: 就是创建…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
