备战蓝桥杯---牛客寒假训练营2VP
题挺好的,收获了许多
1.暴力枚举(许多巧妙地处理细节方法)

n是1--9,于是我们可以直接暴力,对于1注意特判开头0但N!=1,对于情报4,我们可以把a,b,c,d的所有取值枚举一遍,那么如何判断有无前导0?我们只要与10000...比即可,最后用2和3判断一下放入set中去重。
这里有一个小性质:判断是否可以被8除只要看后3位,因为前面的都乘了1000.
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int t,n,y;
string s;
void solve(){set<int>st;if(s[0]=='0'&&n!=1){cout<<0;return;}int mi=1;for(int i=2;i<=n;i++) mi*=10;if(n==1) mi=0;for(int a=0;a<=9;a++){for(int b=0;b<=9;b++){for(int c=0;c<=9;c++){for(int d=0;d<=9;d++){if(a==b||a==c||a==d||b==c||b==d||c==d) continue;for(int _=0;_<=9;_++){int x=0;for(int j=0;j<n;j++){if(s[j]<='9'&&s[j]>='0'){x=x*10+(s[j]-'0');}else{if(s[j]=='a'){x=x*10+a;}else if(s[j]=='b'){x=x*10+b;}else if(s[j]=='c'){x=x*10+c;}else if(s[j]=='d'){x=x*10+d;}else{x=x*10+_;}}}if(x>=mi&&x<=y&&x%8==0) st.insert(x); }}}}}cout<<st.size()%mod;
}
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>t;while(t--){cin>>n>>s>>y;solve();cout<<endl;}
}2.思维:

我们不妨把绝对值拆开,发现它就是两个点的min的两倍,那么对于任意两个点最小dis可能是这两个点较小的2倍,也可能是绕过最小点a[1]的4倍。
于是我们sort一下,从小到大枚举每一个点的贡献即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,t,a[200010];
bool cmp(int a,int b){return a<b;
}
void solve(){cin>>n;for(int i=1;i<=n;i++) scanf("%d",&a[i]);sort(a+1,a+n+1,cmp);long long sum=0;for(int i=1;i<=n;i++){sum+=4ll*min(2*a[1],a[i])*(n-i);}cout<<sum;
}
int main(){cin>>t;while(t--){solve();cout<<endl;}
}3.DP

直接按照题目要求DP会TLE,因此我们可以预先维护好每一张卡牌走1---n步的最小花费,同时注意到modn的性质,走n次一定会回到原点以此判断结尾。
dp[i][j]表示最大走i步后使聚合卡提高到j的最小代价,dp[0][0]=0,求dp[n][n-k],易得状态转移方程:
dp[i][j]=min(dp[i-1][j],dp[i-1][(j-i+n)%n]+min[i]),其中我们只用减一个i即可(因为走更多的话就不满足最大走i步的条件)
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
long long t,n,m,k,c[1110],a[1100],mins[5005],dp[5005];
bool vis[5002];
void solve(){for(int i=0;i<=n;i++) mins[i]=2e18; for(int i=0;i<=n;i++) dp[i]=2e18;for(int i=1;i<=m;i++){for(int j=1;;j++){if((a[i]*j)%n==a[i]%n&&j>1) break;int u=(a[i]*j)%n;mins[u]=min(mins[u],c[i]*j);}}dp[0]=0;for(int i=1;i<=n;i++){for(int j=0;j<=n;j++){dp[j%n]=min(dp[j%n],dp[(j-i+n)%n]+mins[i]);}}long long ww=dp[n-k];if(ww>=2e18) cout<<-1;else cout<<ww;return;
}
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>t;while(t--){cin>>n>>m>>k;for(int i=1;i<=m;i++) cin>>a[i]>>c[i];solve();cout<<endl;}
}相关文章:

备战蓝桥杯---牛客寒假训练营2VP
题挺好的,收获了许多 1.暴力枚举(许多巧妙地处理细节方法) n是1--9,于是我们可以直接暴力,对于1注意特判开头0但N!1,对于情报4,我们可以把a,b,c,d的所有取值枚举一遍,那么如何判断有…...
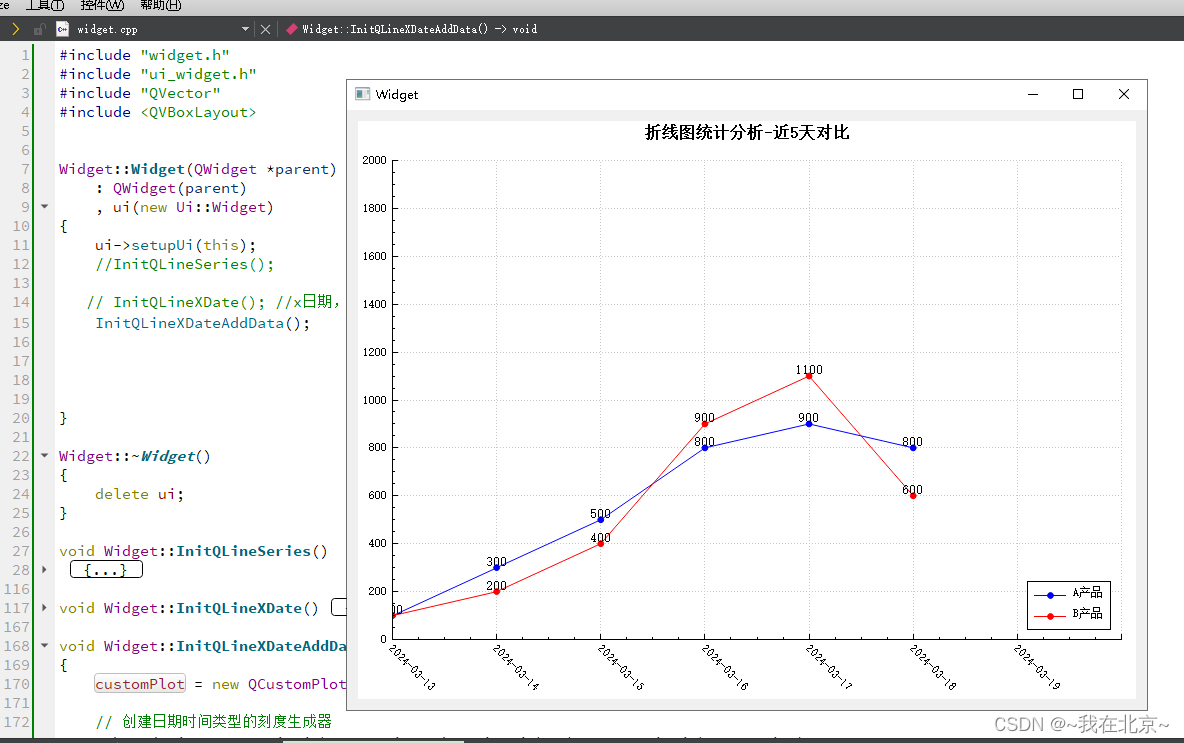
QCustomPlot-绘制X轴为日期的折线图
主要代码如下: void Widget::InitQLineXDateAddData() {customPlot new QCustomPlot(this);// 创建日期时间类型的刻度生成器QSharedPointer<QCPAxisTickerDateTime> dateTimeTicker(new QCPAxisTickerDateTime);dateTimeTicker->setDateTimeFormat(&quo…...
腾讯春招后端一面(算法篇)
前言: 哈喽大家好,前段时间在小红书和牛客上发了面试的经验贴,很多同学留言问算法的具体解法,今天就详细写个帖子回复大家。 因为csdn是写的比较详细,所以更新比较慢,大家见谅~~ 就题目而言,…...

Filebeat rpm方式安装及配置
一、使用服务器root用户、filebeat8.11.1版本,rpm安装方式进行安装 curl -L -O https://artifacts.elastic.co/downloads/beats/filebeat/filebeat-8.11.1-x86_64.rpm sudo rpm -vi filebeat-8.11.1-x86_64.rpm 二、配置核心的采集文件、使用inputs热更方式、配置filebeat本身…...

深入挖掘C语言之——枚举
目录 1. 枚举的定义 2. 枚举常量的赋值 3. 枚举的使用示例 4. 注意事项 在C语言中,枚举(Enum)是一种用户定义的数据类型,用于定义一组具名的整型常量。枚举常常用于提高代码的可读性和可维护性,使程序更易于理解。…...
【源码阅读】EVMⅢ
参考[link](https://blog.csdn.net/weixin_43563956/article/details/127725385 大致流程如下: 编写合约 > 生成abi > 解析abi得出指令集 > 指令通过opcode来映射成操作码集 > 生成一个operation 以太坊虚拟机的工作流程: 由solidity语言编…...
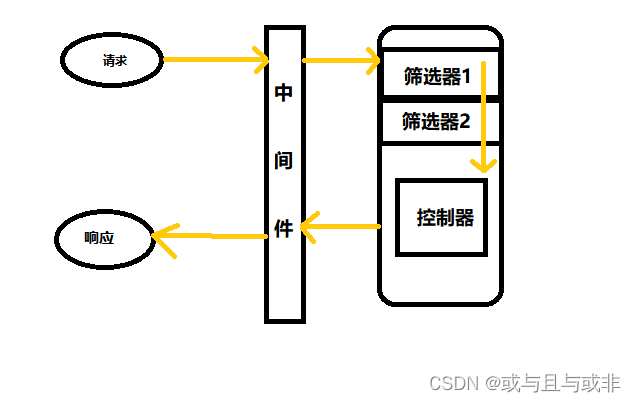
.Net Core 中间件验签
文章目录 为什么是用中间件而不是筛选器?代码实现技术要点context.Request.EnableBuffering()指针问题 小结 为什么是用中间件而不是筛选器? 为什么要用中间件验签,而不是筛选器去验签? 1、根据上图我们可以看到,中间件在筛选器之…...
Elasticsearch:从 Java High Level Rest Client 切换到新的 Java API Client
作者:David Pilato 我经常在讨论中看到与 Java API 客户端使用相关的问题。 为此,我在 2019 年启动了一个 GitHub 存储库,以提供一些实际有效的代码示例并回答社区提出的问题。 从那时起,高级 Rest 客户端 (High Level Rest Clie…...
七:分布式
一、Nginx nginx安装 【1】安装pcre依赖 1.下载压缩包:wget http://downloads.sourceforge.net/project/pcre/pcre/8.37/pcre-8.37.tar.gz 2.解压压缩包:tar -xvf pcre-8.37.tar.gz 3.安装gcc:yum install gcc 4.安装gcc:yum ins…...
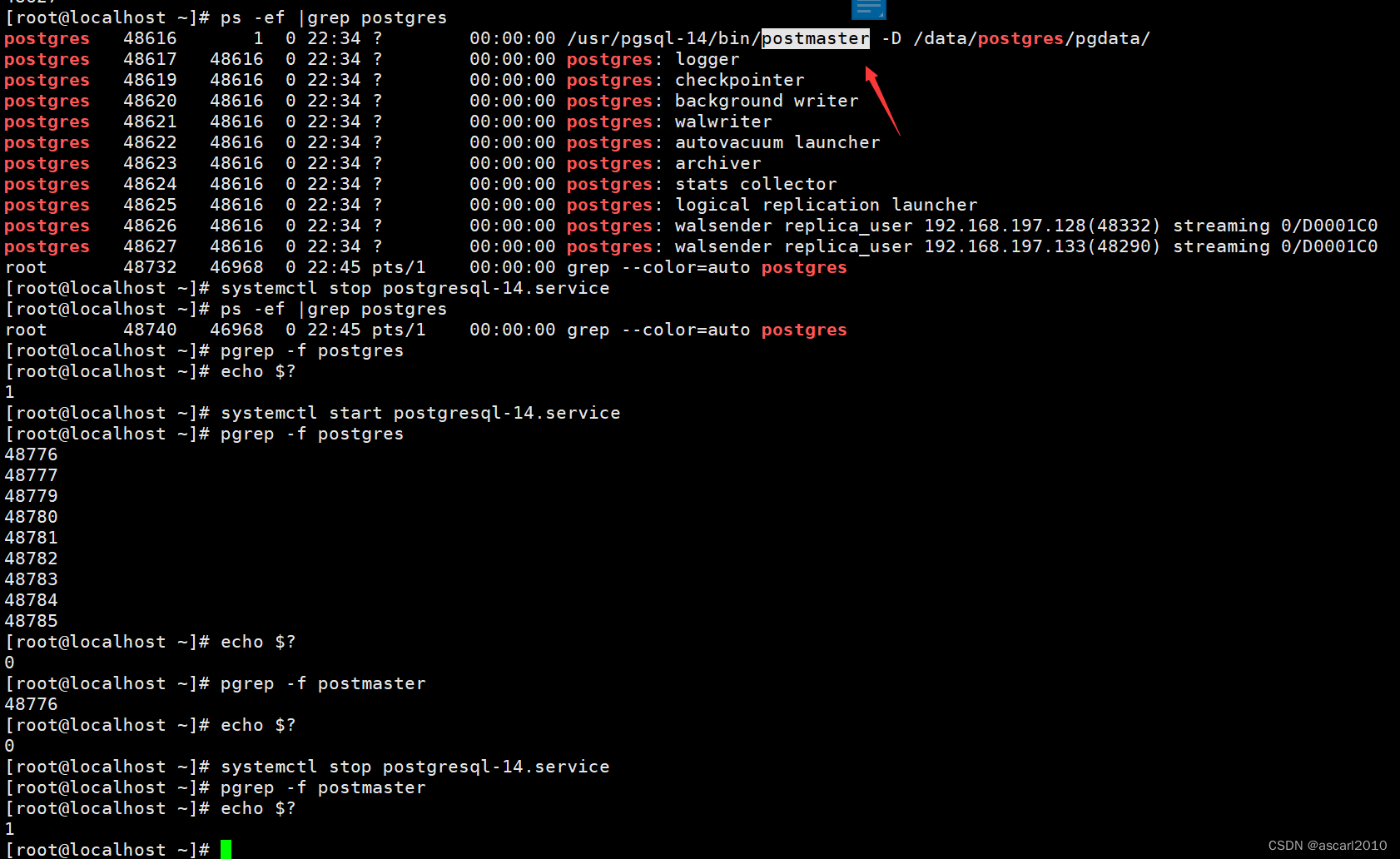
1-postgresql数据库高可用脚本详解
问题: pgrep -f postgres > /dev/null && echo 0 || pkill keepalived 这是什么意思 建议换成 pgrep -f postmaster > /dev/null && echo 0 || pkill keepalived 回答 这条命令是一个复合命令,包含条件执行和重定向的元素。让我们…...

【亲测】Onlyfans年龄认证怎么办?Onlyfans需要年龄验证?
1. 引言 什么是OnlyFans:OnlyFans是一种内容订阅服务,成立于2016年,允许内容创作者从用户那里获得资金,用户需要支付订阅费用才能查看他们的内容。它在多个领域受到欢迎,包括音乐、健身、摄影,以及成人内容…...

ASP.NET Core新特性
1. ASP.NET Core2.1 ASP.NET Core 2.1于2018年5月30日发布。是ASP.NET Core框架的一个重要版本,带来了许多新功能和改进。以下是ASP.NET Core 2.1中一些主要的特性: SignalR:引入了 SignalR,这是一个实时通信库,使得构…...
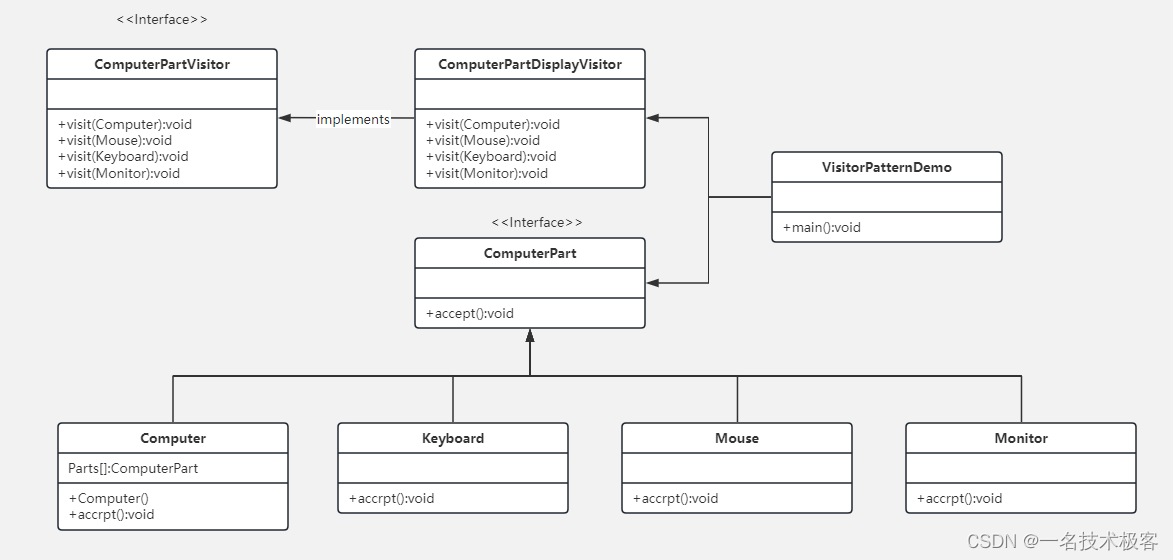
26-Java访问者模式 ( Visitor Pattern )
Java访问者模式 摘要实现范例 访问者模式(Visitor Pattern)使用了一个访问者类,它改变了元素类的执行算法,通过这种方式,元素的执行算法可以随着访问者改变而改变访问者模式中,元素对象已接受访问者对象&a…...
电子科技大学链时代工作室招新题C语言部分---题号G
1. 题目 问题的第一段也是非常逆天,说实话,你编不出问题背景可以不编。 这道题的大概意思就是, Pia要去坐飞机,那么行李就有限重。这时Pia想到自己带了个硬盘,众所周知,硬盘上存储的数据就是0和1的二进制序…...
体育运动直播中的智能运动跟踪和动作识别系统 - 视频分析如何协助流媒体做出实时决策
AI-Powered Streaming Vision: Transforming Real-Time Decisions with Video Analytics 原著:弗朗西斯科冈萨雷斯|斯特朗(STRONG)公司首席ML科学家 翻译:数字化营销工兵 实时视频分析通过即时处理实时视频数据&…...

Avalon总线学习
Avalon总线学习 avalon总线可以分为: Avalon clock interface Avalon reset interface Avalon Memory mapped interface Avalon iterrupt interface Avalon streaming interface Avalon tri-state conduit interface Avalon conduit interface 1、Avalon c…...
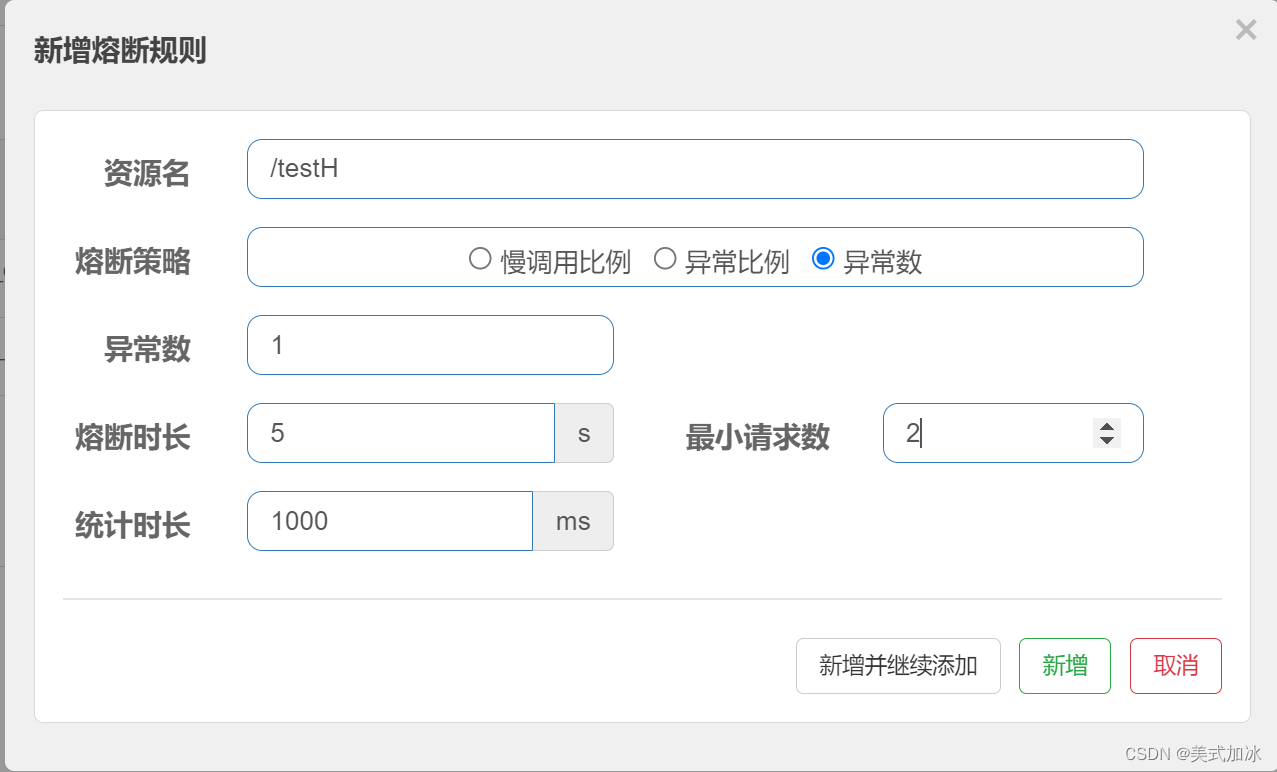
Sentinel(熔断规则)
慢调用比例 慢调用比例( SLOM_REQUEST_RATTo ):选择以慢调用比例作为阈值,需要设置允许的慢调用RT(即最大的响应时间),请求的响应时间大于该值则统计为慢调用。当单位统计时长(statIntervalMs)内请求数目大于设置的最小请求数目,…...

Hive借助java反射解决User-agent编码乱码问题
一、需求背景 在截取到浏览器user-agent,并想保存入数据库中,经查询发现展示的为编码后的结果。 现需要经过url解码过程,将解码后的结果保存进数据库,那么有几种实现方式。 二、问题解决 1、百度:url在线解码工具 …...
Linux下安装Android Studio及创建桌面快捷方式
下载 官网地址:https://developer.android.com/studio?hlzh-cn点击下载最新版本即可 安装 将下载完成后文件,进行解压,然后进入android-studio-2023.2.1.23-linux/android-studio/bin目录下,启动studio.sh即可为了更加方便的使…...
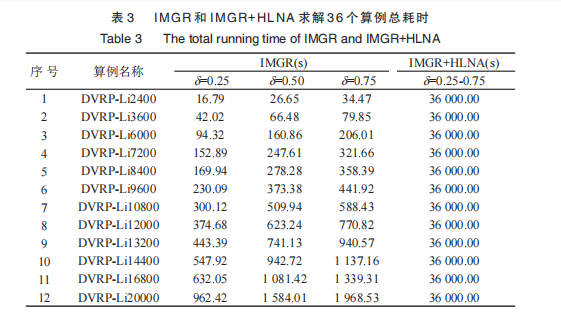
【析】一类动态车辆路径问题模型和两阶段算法
一类动态车辆路径问题模型和两阶段算法 摘要 针对一类动态车辆路径问题,分析4种主要类型动态信息对传统车辆路径问题的本质影响,将动态车辆路径问题(Dynamic Vehicle Routing Problem, DVRP)转化为多个静态的多车型开放式车辆路径问题(The Fleet Size a…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...
