第二门课:改善深层神经网络<超参数调试、正则化及优化>-超参数调试、Batch正则化和程序框架
文章目录
- 1 调试处理
- 2 为超参数选择合适的范围
- 3 超参数调试的实践
- 4 归一化网络的激活函数
- 5 将Batch Norm拟合进神经网络
- 6 Batch Norm为什么会奏效?
- 7 测试时的Batch Norm
- 8 SoftMax回归
- 9 训练一个SoftMax分类器
- 10 深度学习框架
- 11 TensorFlow
1 调试处理
需要调试的参数:α是最重要的。
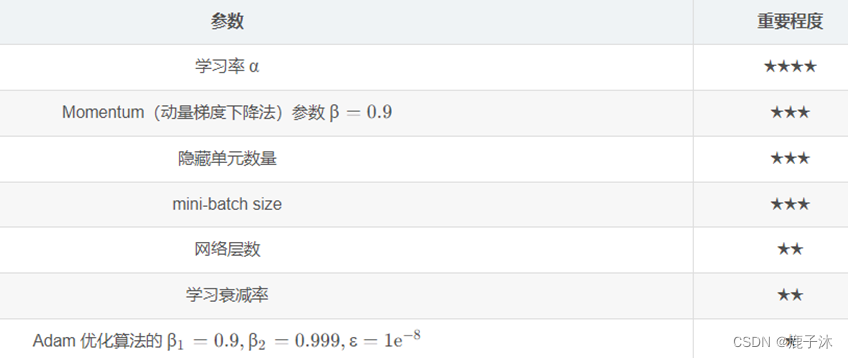
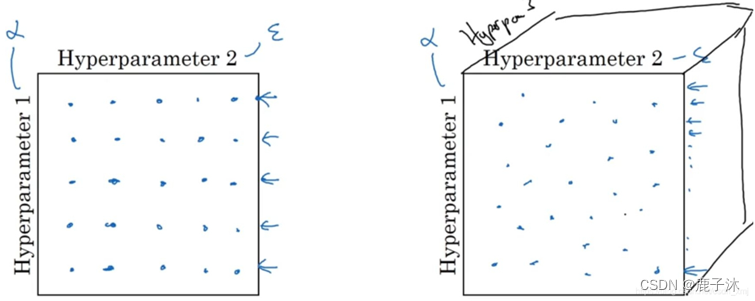
可以采用随机取值,然后选择哪个参数的效果更好。

由粗糙到精细的策略。即放大表现较好的区域(即小篮框内),然后在其中更密集的取值或随机取值。
2 为超参数选择合适的范围
对于某些超参数(隐藏单元的数量或者神经网络的层数)是可以进行尺度均匀采样的。
某些超参数需要选择不同的合适尺度进行随机采样。随机取值,并不是在范围内均匀取值。
使用对数标尺搜索超参数的方式会更合理
1>比如想取参数 α∈[0.0001,1]
r = -4*np.random.rand(), r∈[−4,0],然后取 α=10r,在 r 的区间均匀取值
2>再比如计算指数的加权平均值参数 β∈[0.9,0.999]
我们考察 1−β∈[0.001,0.1],那么我们令r∈[−3,−1], r 在里面均匀取值, β=1−10r
因为加权平均值大概是基于过去 1\1−β个值进行平均,当 β接近 1 的时候,对细微的变化非常敏感,需要更加密集的取值
当然,如果你使用均匀取值,应用从粗到细的搜索方法,取足够多的数值,最后也会得到不错的结果。
3 超参数调试的实践
在数据更新后,要重新评估超参数是否依然合适
没有计算资源,你可以试验一个或者少量的模型,不断的调试和观察效果(熊猫式)
有计算资源,尽管试验不同参数的模型,最后选择一个最好的(鱼子酱式)
4 归一化网络的激活函数
Batch归一化 会使你的参数搜索问题变得很容易,使神经网络对超参数的选择更加稳定,超参数的范围会更加庞大,工作效果也很好,也会使你的训练更加容易.
对于任意一层的输入 我们将其归一化 z1
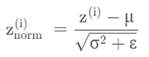
但是我们不想让每一层的均值都为0,方差为1,也许有不同的分布有意义,加上2个超参数 γ,β
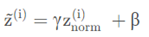
γ和β的作用是使隐藏单元值的均值和方差标准化,即z^(i)有固定的均值和方差,均值和方差可以是0和1,也可以是其它值,它是由γ和β两参数控制的。
当γ=\sqrt{σ^2+ε}, β=μ时,那么z(i)波浪线 = z(i)
5 将Batch Norm拟合进神经网络
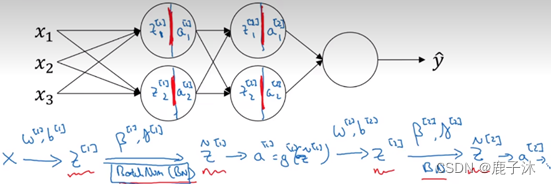
Batch归一化的做法是将z[l]值进行Batch归一化,简称BN,此过程将由β[l]和γ[l]两参数控制,这一操作会给出一个寻得规范化的z[l]值<z[l]波浪线>,然后将其输入激活函数中得到a[l],即a[l]=gl。
注意:
1>需要强调的是Batch归一化时发生在计算z和a之间的。
2>这里的β,β[1], β[2]和超参数β没有任何关系,Batch归一化中使用β代表此参数(β[1], β[2]等等),而后者是用于Momentum或计算各个指数的加权平均值。

Mini-batch中与Batch中训练方式相同。

总结用Batch归一化来应用梯度下降法:

6 Batch Norm为什么会奏效?
1 使得输入特征、隐藏单元的值获得类似的范围,可以加速学习。
2 在前面层输入值改变的情况下,BN 使得他们的均值和方差不变(更稳定),即使输入分布改变了一些,它会改变得更少。
它减弱了前层参数的作用与后层参数的作用之间的联系,它使得网络每层都可以自己学习,稍稍独立于其它层,这有助于加速整个网络的学习。
另外,BN 有轻微的正则化效果,因为它在 mini-batch 上计算的均值和方差是有小的噪声,给隐藏单元添加了噪声,迫使后部单元不过分依赖任何一个隐藏单元(类似于 dropout),当增大 mini-batch size ,那么噪声会降低,因此正则化效果减弱。
注:Batch归一化一次只能处理一个mini-batch数据。
7 测试时的Batch Norm

在一个mini-batch中,计算均值和方差,这里用m表示mini-batch中样本数量,而不是整个数据集。注意到μ和σ2是对单个mini-batch中所有m个样本求得的。
用指数加权平均来估算, 这个平均数涵盖了所有 mini-batch (训练过程中计算 μ,σ2 的加权平均)
8 SoftMax回归
SoftMax回归适用于多分类问题
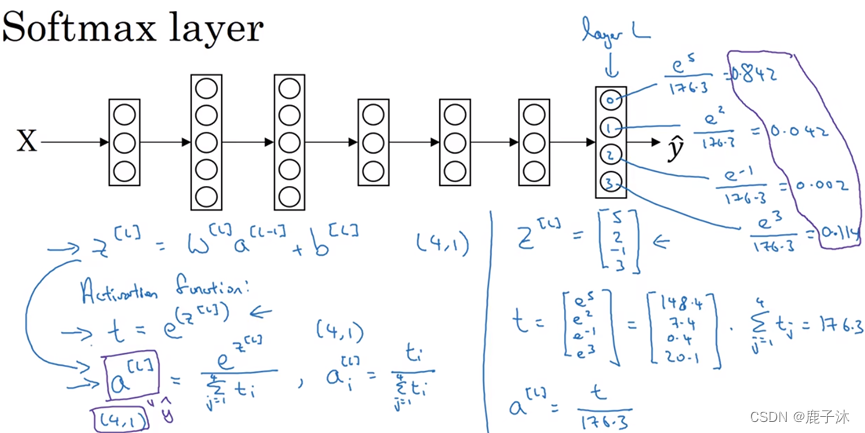
在神经网络最后一层
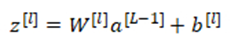
然后计算一个临时变量
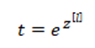
最后将其进行归一化
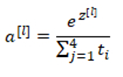
SoftMax激活函数与众不同之处在于需要输入一个4×1维向量,然后输出一个4×1维向量。之前,我们的激活函数都是接受单行数值输入,例如Sigmoid和ReLU激活函数,输入一个实数,输出一个实数。SoftMax激活函数的特殊之处在于,因为需要将所有可能的输出归一化,就需要输入一个向量,最后输出一个向量。
没有隐藏层的神经网络:
输出分类的SoftMax层能够代表这种类型的决策边界,请注意这是几条线性决策边界
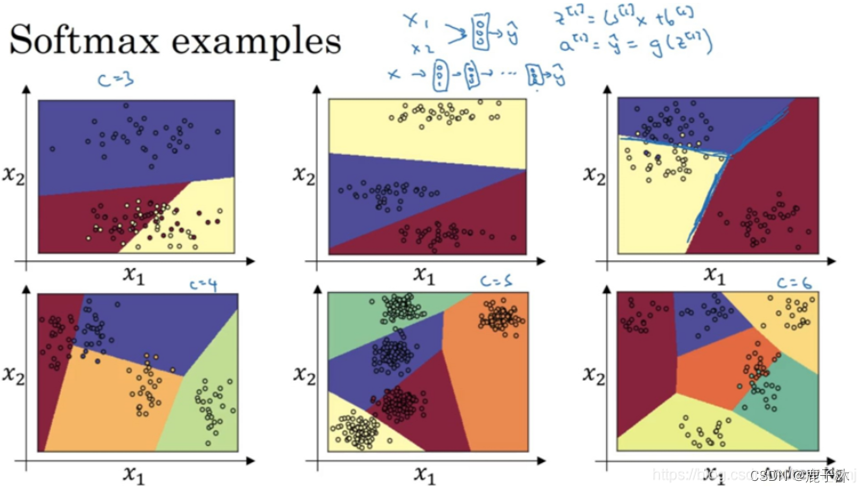
9 训练一个SoftMax分类器
SoftMax回归或SoftMax激活函数将logistic激活函数推广到C类,而不仅仅是两类,结果就是如果C=2,那么C=2的SoftMax实际上变回了logistic回归。
训练集中某个样本的真实标签是[0 1 0 0],上个视频中这表示猫,目标输出y帽=[0.3 0.2 0.1 0.4],这里只分配20%是猫的概率,所以这个神经网络在本例中表现不佳。
单个函数的训练集损失函数:
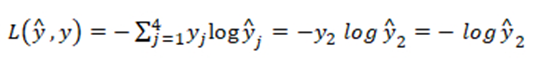
试图将损失函数L变小,因为梯度下降法是用来减少训练集的损失的,要使它变小的唯一方式就是使y2帽尽可能大,即这项输出概率尽可能的大。
整个训练集损失函数:
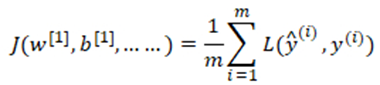
初始化反向传播的关键步骤:
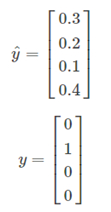
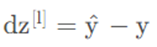
10 深度学习框架

选择框架的标准:
1、便于编程,既包括神经网络的开发和迭代,还包括为产品进行配置
2、运行速度,特别是训练大数据集时,一些框架能让你更高效的运行和训练神经网络。
3、框架是否真的开放,不仅需要开源,而且需要良好的管理。
11 TensorFlow
import numpy as np
import tensorflow as tf#接下来,让我们定义参数w,在TensorFlow中,你要用tf.Variable()来定义参数
w = tf.Variable(0,dtype = tf.float32) # 定义损失函数 w**2-10w+25
#cost = tf.add(tf.add(w**2,tf.multiply(- 10.,w)),25)
#TensorFlow还重载了一般的加减运算等,因此可以表示为以下形式
cost = w**2-10*w+25#让我们用0.01的学习率,目标是最小化损失
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost) #最后下面的几行是惯用表达式:
init = tf.global_variables_initializer()
session = tf.Sessions()
#这样就开启了一个TensorFlow session。
session.run(init)
#来初始化全局变量。
#然后让TensorFlow评估一个变量,我们要用到: session.run(w)
#上面的这一行将w初始化为0,并定义损失函数,我们定义train为学习算法,它用梯度下降法优化器使损失函数最小化,但实际上我们还没有运行学习算法,
#所以session.run(w)评估了w,让我们打印结果:
print(session.run(w))
#所以如果我们运行这个,它评估等于0,因为我们什么都还没运行。#运行一步梯度下降法。
session.run(train)
#让我们评估一下w的值
print(session.run(w))
#0.1
#在一步梯度下降法之后,w现在是0.1。#现在我们运行梯度下降1000次迭代:
for i in range(1000):session.run(train)
print(session.ran(w))
#输出结果:4.99999,与5很接近了。
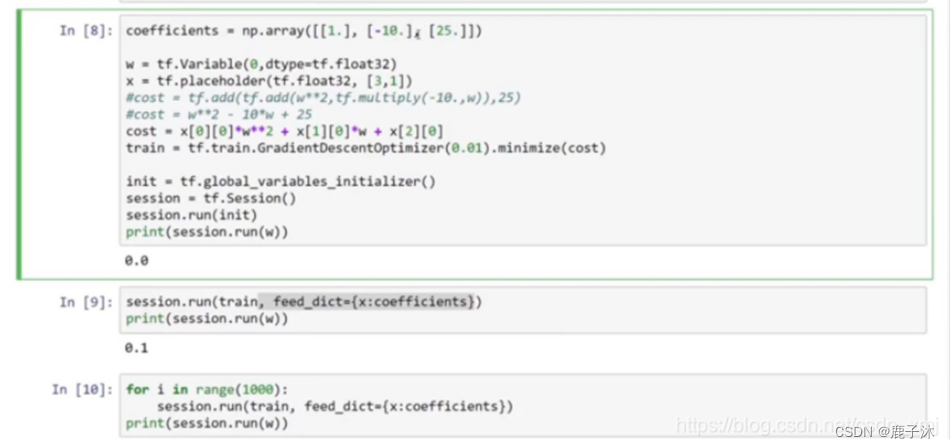
#具体代码讲解:
#让它成为[3,1]数组,因为这个二次方程的三项前有固定的系数,我们可以把这些数字1,-10和25变成数据
x = tf.placeholder(tf.float32,[3,1])
#现在x变成了控制这个二次函数系数的数据,这个placeholder函数告诉TensorFlow,你稍后会为x提供数值。
cost = x[0][0]*w**2 +x[1][0]*w + x[2][0]#让我们再定义一个数组(array),
coefficient = np.array([[1.],[-10.],[25.]])#这就是我们要接入x的数据。最后我们需要用某种方式把这个系数数组接入变量x,做到这一点的句法是,在训练这一步中,要提供给x的数值,在这里设置:
feed_dict = {x:coefficients}

with结构也会在很多TensorFlow程序中用到,它的意思基本上和左边的相同,但是Python中的with命令更方便清理,以防在执行这个内循环时出现错误或例外。
l ↩︎
相关文章:

第二门课:改善深层神经网络<超参数调试、正则化及优化>-超参数调试、Batch正则化和程序框架
文章目录 1 调试处理2 为超参数选择合适的范围3 超参数调试的实践4 归一化网络的激活函数5 将Batch Norm拟合进神经网络6 Batch Norm为什么会奏效?7 测试时的Batch Norm8 SoftMax回归9 训练一个SoftMax分类器10 深度学习框架11 TensorFlow 1 调试处理 需要调试的参…...
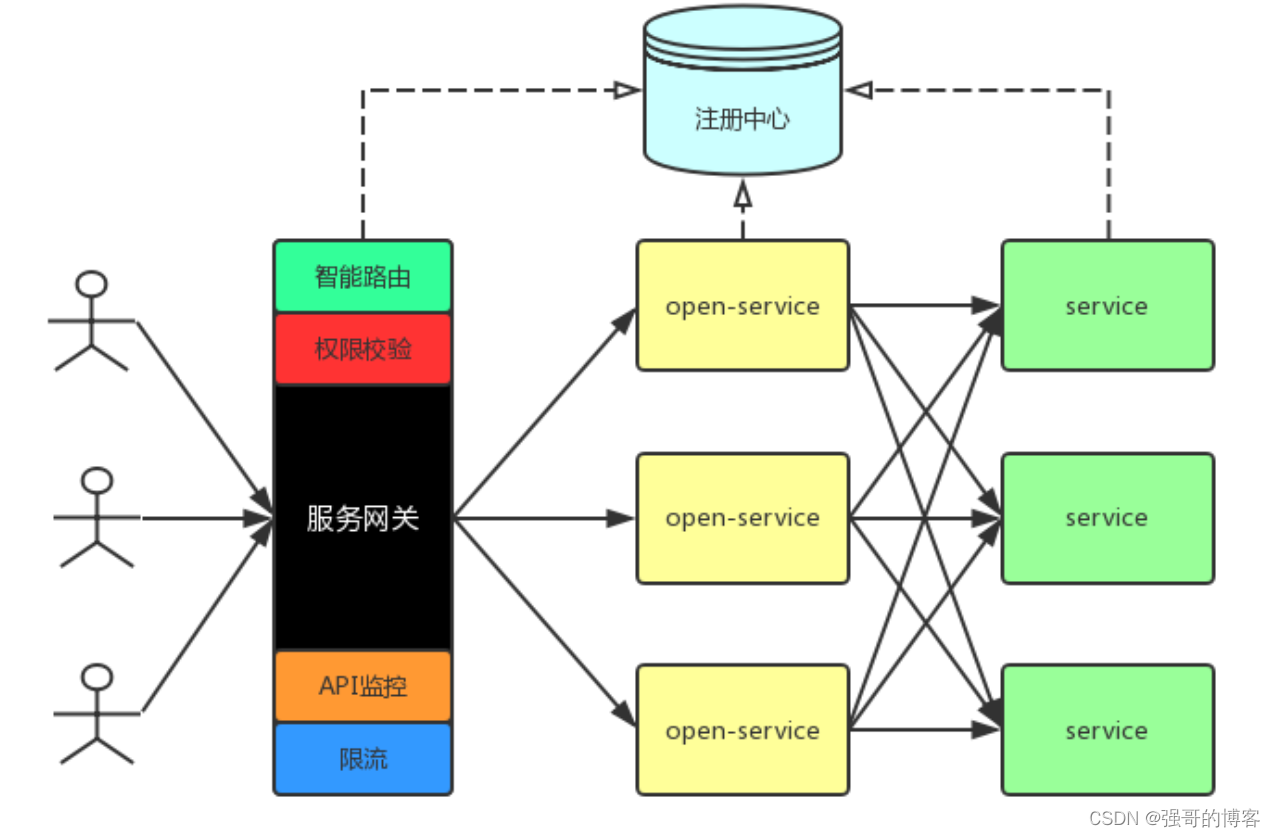
漫谈微服务网关
一、什么是服务网关 服务网关 路由转发 过滤器 1、路由转发:接收一切外界请求,转发到后端的微服务上去; 2、过滤器:在服务网关中可以完成一系列的横切功能,例如权限校验、限流以及监控等,这些都可以通过…...

进击的PostgreSQL
目录 前言 一、什么是PostgreSQL 1.PostgreSQL的定义 2.PostgreSQL功能和特性 2.1数据类型 2.2数据完整性 2.3并发性、性能 2.4可靠性、灾难恢复 2.5安全 2.6扩展 2.7国际化、文本搜索 二、部署PostgreSQL 1.下载与安装 2.配置数据库 3.配置远程访问 4.修改配置…...
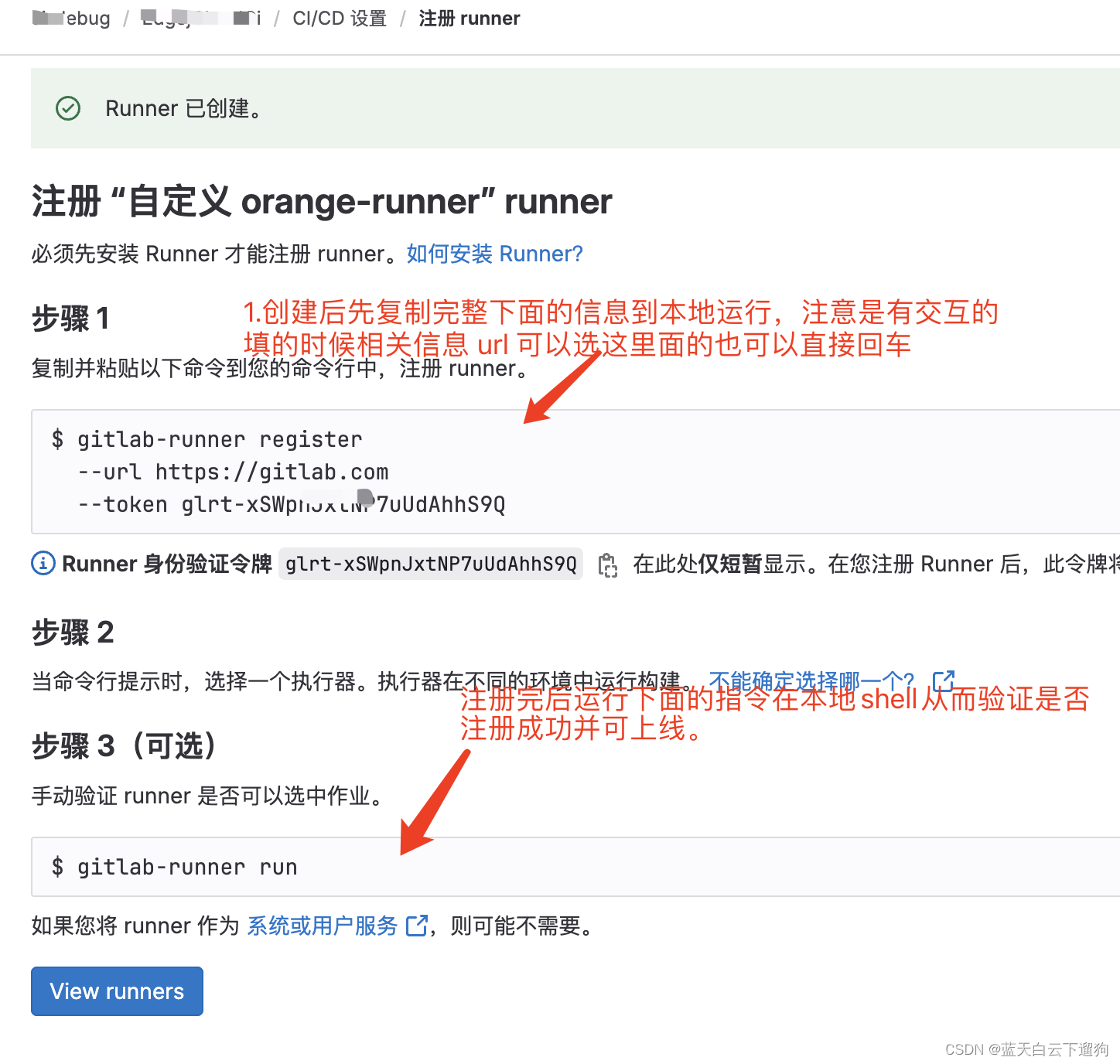
本地gitlab-runner的创建与注册
引言 之前通过一些方式在本地创建runner,时而会出现一些未知的坑,所以写下本文记录runner可以无坑创建的方式。 以下注册runner到相应仓库的前提是已经在本地安装了gitlab-runner 具体安装方式见官网 本地gitlab-runner安装常用的指令 查看gitlab r…...

《UE5_C++多人TPS完整教程》学习笔记28 ——《P29 Mixamo 动画(Mixamo Animations)》
本文为B站系列教学视频 《UE5_C多人TPS完整教程》 —— 《P29 Mixamo动画(Mixamo Animations)》 的学习笔记,该系列教学视频为 Udemy 课程 《Unreal Engine 5 C Multiplayer Shooter》 的中文字幕翻译版,UP主(也是译者…...

剑指offer力扣题集
剑指offer Krahets前辈整理的题解,这个博客为了方便自己刷题和复习,加油! 01. 数组中重复的数字 力扣链接 02. 二维数组中的查找 力扣链接 03. 替换空格 力扣链接 04. 从尾到头打印链表 力扣链接 05. 重建二叉树 力扣链接好难 -_-…...

【商业|数据科学主题会议推荐】2024年商业分析与数据科学国际学术会议(ICBADS 2024)
【商业|数据科学主题会议推荐】2024年商业分析与数据科学国际学术会议(ICBADS 2024) 征稿主题 (以下主题包括但不限于) 多媒体决策 决策理论与决策科学 数字市场设计与运营 降维 电子商务 道德决策 财务分析 群体决策与软件 医疗保…...

爬虫技术实战案例解析
目录 前言 案例背景 案例实现 案例总结 结语 前言 作者简介: 懒大王敲代码,计算机专业应届生 今天给大家聊聊爬虫技术实战案例解析,希望大家能觉得实用! 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!…...
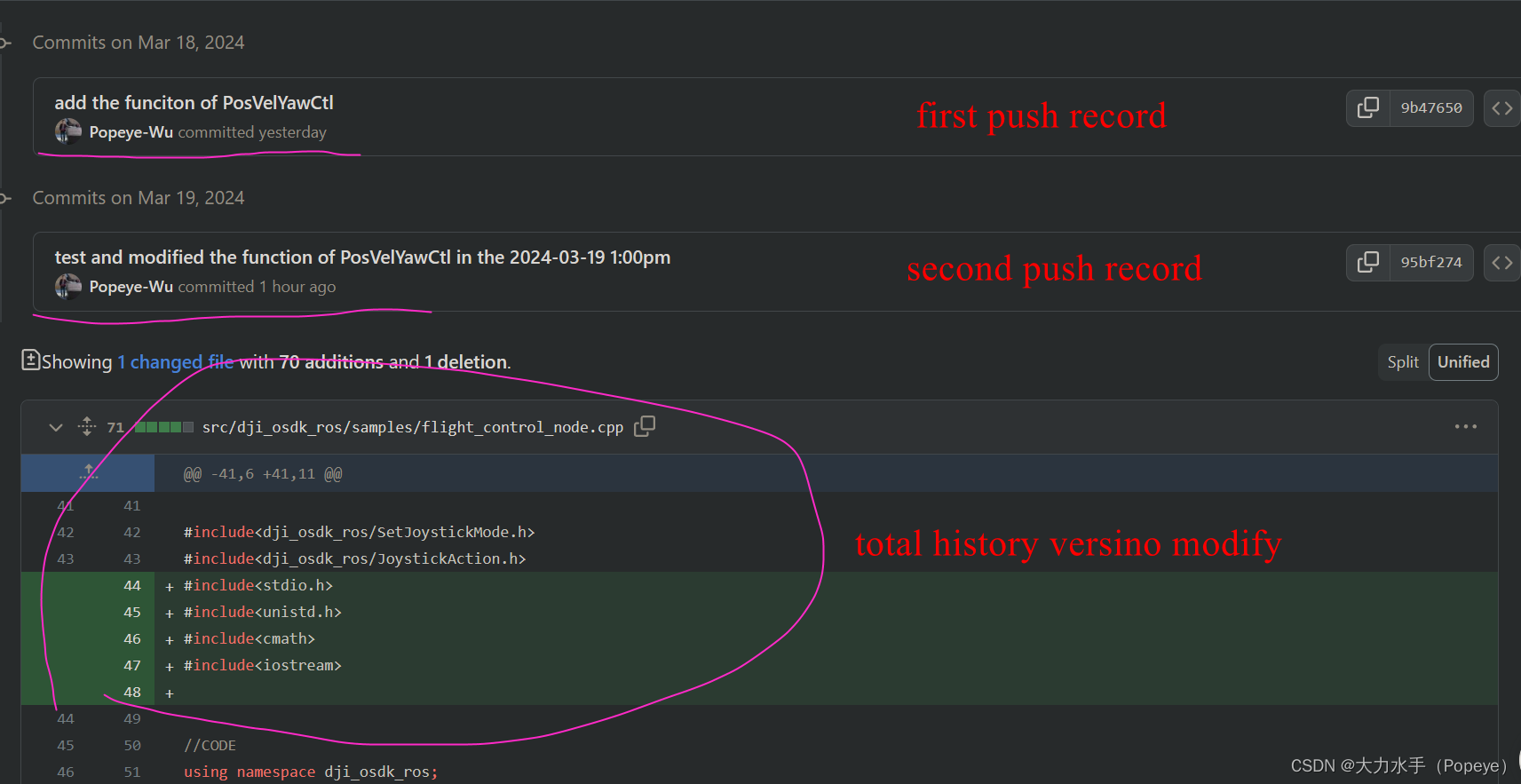
Git 使用笔记
基本操作: 初始化 (git init) 使用背景和作用: 在本地建立一个文件夹后,基于这个文件夹进行git 操作,赋予git操作本文件夹的权限 。查看当前文件夹状态(git status) 每次打开文件夹…...

python -- 语法与变量
你好, 我是木木, 目前正在做两件事 1. 沉淀自己的专业知识 2. 探索了解各种副业项目,同时将探索过程进行分享,帮助自己以及更多朋友找到副业, 做好副业 文末有惊喜 语法的简要说明 每种语言都有自己的语法,不管是自然语言(…...

24计算机考研调剂 | 太原科技大学
2024年太原科技大学 力学专业 接收研究生调剂通告 考研调剂招生信息 招生专业: 080100(力学) 01先进材料变形行为及力学性能 02 计算力学及其应用 03结构动力学与无损检测 04复合材料断裂理论与结构设计 补充内容 调剂考生基本要求 &…...

Leetcode 204. 计数质数 java题解
https://leetcode.cn/problems/count-primes/description/ 法一 class Solution {public int countPrimes(int n) {int count0;for(int i2;i<n;i){//判断i是否质数boolean ftrue;for(int j1;j*j<i;j){//因子if(j!1&&j!i&&(i%j0)){ffalse;break;}}if(f){…...
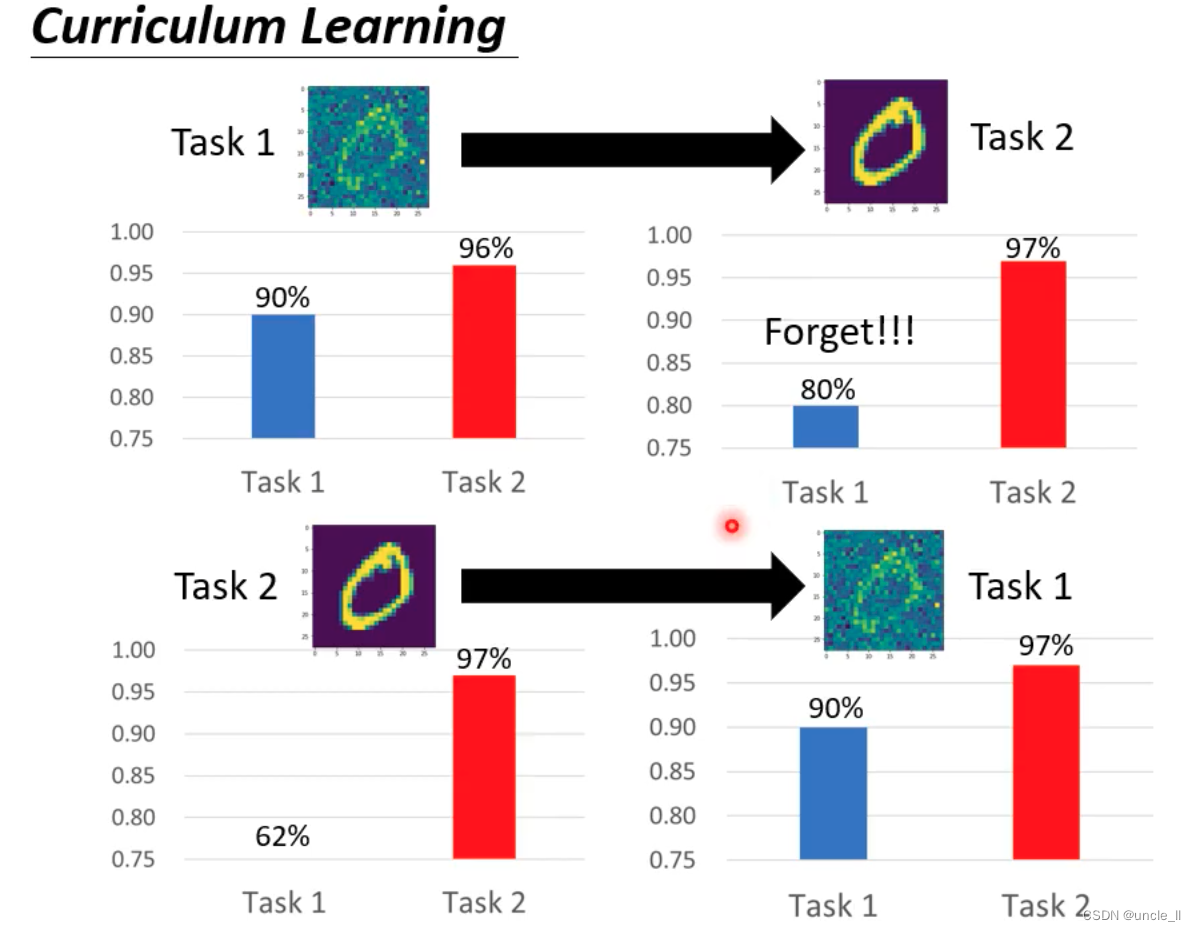
机器学习——终身学习
终身学习 AI不断学习新的任务,最终进化成天网控制人类终身学习(LLL),持续学习,永不停止的学习,增量学习 用线上收集的资料不断的训练模型 问题就是对之前的任务进行遗忘,在之前的任务上表现不好…...
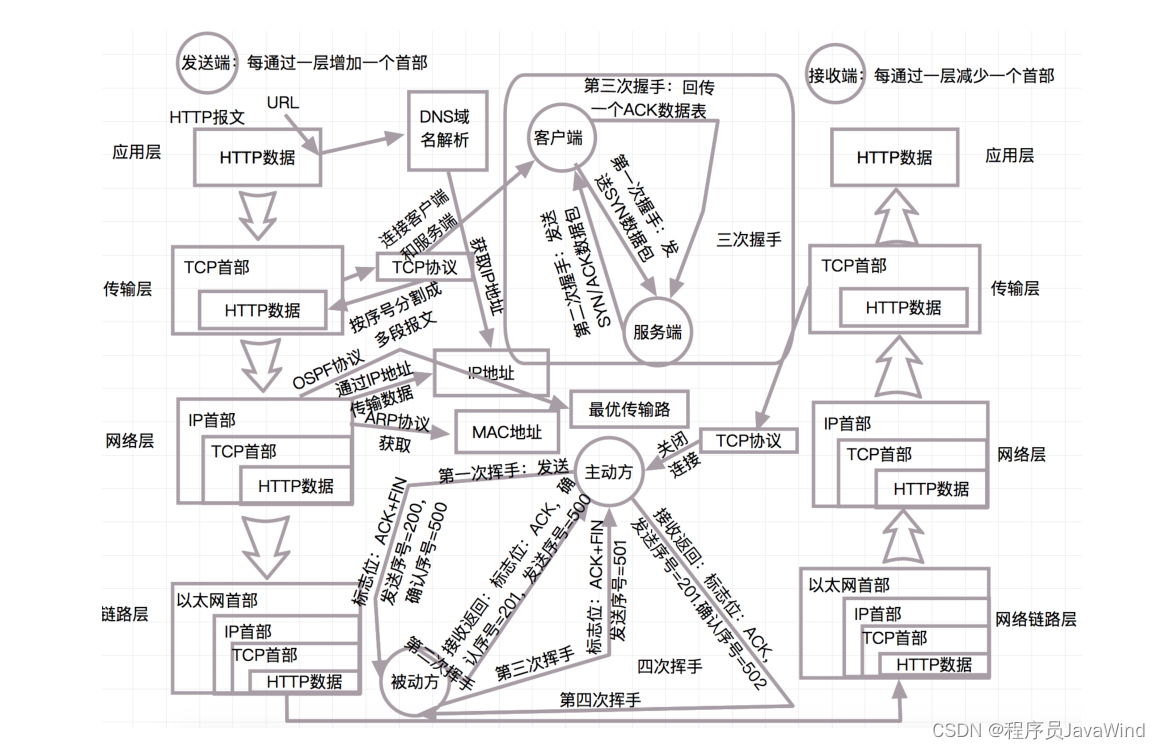
一次完整的 HTTP 请求所经历的步骤
1: DNS 解析(通过访问的域名找出其 IP 地址,递归搜索)。 2: HTTP 请求,当输入一个请求时,建立一个 Socket 连接发起 TCP的 3 次握手。如果是 HTTPS 请求,会略微有不同。 3: 客户端向服务器发…...

OpenGL学习笔记【1】——简介
一、OpenGL概念 OpenGL (Open Graphics Library,译名:开放式图形库开放式图形库) 是一种用于渲染 2D 和 3D 图形的跨语言、跨平台的编程接口(API)。 二、OpenGL跨语言 OpenGL 是一个 C 语言库,因此理解 C 语言(或 C)的…...

C语言课后作业 20 题+考研上机应用题
题目 1: 计算圆的面积 描述: 输入圆的半径,计算并输出圆的面积。 题目 2: 判断一个年份是否为闰年 描述: 输入一个年份,判断并输出该年份是否为闰年。 题目 3: 计算并输出斐波那契数列的前10个数 描述: 输出斐波那…...

macOS上基于httpd-dav搭建WebDav服务
文章目录 配置 Apache httpd修改 ServerName启动验证 httpd 服务启用 Dav 扩展服务配置 配置 httpd 扩展 Dav 服务设置共享目录文件夹配置 DavLockDB 目录创建 WebDAV 访客用户 httpd-dav.conf 主要改动部分BasicDigest共享多个目录 授予 httpd 完全磁盘访问权限验证更新配置重…...

Java-设计模式-单例模式
单例模式 从单例加载的时机区分,有懒汉模式/饥饿模式。 从实现方式区分有双重检查模式,内部类模式/Enum模式/Map模式等。在《Effective Java》中,作者提出利用Enum时实现单例模式的最佳实践。 内容概要 实现单例模式的几个关键点 利用Enu…...

图片html5提供的懒加载与vue-lazyload的区别
原生HTML lazy loading特性 <img src"/images/ocean.jpeg" alt"Ocean" loading"lazy"> loading"lazy" 是HTML5的一个原生特性,它允许浏览器延迟加载图片直至图片距离视口很近或者即将进入视口时。这是一种由浏览器…...

golang 根据某个特定字段对结构体的顺序进行排序
文章目录 方法一方法二方法三 在Go语言中,我们可以使用 sort.Slice() 函数对结构体进行排序。假设你有一个结构体,并且希望根据其中的某个字段进行排序,你可以使用自定义的排序函数。 方法一 下面是一个示例代码,假设有一个包含…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
