【进阶五】Python实现SDVRP(需求拆分)常见求解算法——差分进化算法(DE)
基于python语言,采用经典差分进化算法(DE)对 需求拆分车辆路径规划问题(SDVRP) 进行求解。
目录
- 往期优质资源
- 1. 适用场景
- 2. 代码调整
- 3. 求解结果
- 4. 代码片段
- 参考
往期优质资源
经过一年多的创作,目前已经成熟的代码列举如下,如有需求可私信联系,表明需要的 问题与算法,原创不宜,有偿获取。
| VRP问题 | GA | ACO | ALNS | DE | DPSO | QDPSO | TS | SA |
|---|---|---|---|---|---|---|---|---|
| CVRP | √ | √ | √ | √ | √ | √ | √ | √ |
| VRPTW | √ | √ | √ | √ | √ | √ | √ | √ |
| MDVRP | √ | √ | √ | √ | √ | √ | √ | √ |
| MDHVRP | √ | √ | √ | √ | √ | √ | √ | √ |
| MDHVRPTW | √ | √ | √ | √ | √ | √ | √ | √ |
| SDVRP | √ | √ | √ | √ |
1. 适用场景
- 求解CVRP
- 车辆类型单一
- 车辆容量小于部分需求节点需求
- 单一车辆基地
2. 代码调整
与CVRP问题相比,SDVRP问题允许客户需求大于车辆容量。为了使得每个客户的需求得到满足,必须派遣一辆或多辆车辆对客户进行服务,也就是需要对客户的需求进行拆分。关于如何进行拆分一般有两种方式:
- 先验拆分策略:提前制定策略对客户的需求(尤其是大于车辆容量的客户需求)进行分解,将SDVRP问题转化为CVRP问题
- 过程拆分策略:在车辆服务过程中对客户需求进行动态拆分
本文采用文献[1]提出的先验分割策略,表述如下:
(1)20/10/5/1拆分规则
- m20 =max{ m ∈ Z + ∪ { 0 } ∣ 0.20 Q m < = D i m\in Z^+ \cup \{0\} | 0.20Qm <= D_i m∈Z+∪{0}∣0.20Qm<=Di }
- m10 =max{ m ∈ Z + ∪ { 0 } ∣ 0.10 Q m < = D i − 0.20 Q m 20 m\in Z^+ \cup \{0\} | 0.10Qm <= D_i-0.20Qm_{20}~ m∈Z+∪{0}∣0.10Qm<=Di−0.20Qm20 }
- m5 =max{ m ∈ Z + ∪ { 0 } ∣ 0.05 Q m < = D i − 0.20 Q m 20 − 0.10 Q m 10 m\in Z^+ \cup \{0\} | 0.05Qm <= D_i-0.20Qm_{20}-0.10Qm_{10} m∈Z+∪{0}∣0.05Qm<=Di−0.20Qm20−0.10Qm10 }
- m1 =max{ m ∈ Z + ∪ { 0 } ∣ 0.01 Q m < = D i − 0.20 Q m 20 − 0.10 Q m 10 − 0.05 Q m 5 m\in Z^+ \cup \{0\} | 0.01Qm <= D_i-0.20Qm_{20}-0.10Qm_{10}-0.05Qm_{5} m∈Z+∪{0}∣0.01Qm<=Di−0.20Qm20−0.10Qm10−0.05Qm5 }
(2)25/10/5/1拆分规则
- m25 =max{ m ∈ Z + ∪ { 0 } ∣ 0.25 Q m < = D i m\in Z^+ \cup \{0\} | 0.25Qm <= D_i m∈Z+∪{0}∣0.25Qm<=Di }
- m10 =max{ m ∈ Z + ∪ { 0 } ∣ 0.10 Q m < = D i − 0.25 Q m 25 m\in Z^+ \cup \{0\} | 0.10Qm <= D_i-0.25Qm_{25}~ m∈Z+∪{0}∣0.10Qm<=Di−0.25Qm25 }
- m5 =max{ m ∈ Z + ∪ { 0 } ∣ 0.05 Q m < = D i − 0.25 Q m 25 − 0.10 Q m 10 m\in Z^+ \cup \{0\} | 0.05Qm <= D_i-0.25Qm_{25}-0.10Qm_{10} m∈Z+∪{0}∣0.05Qm<=Di−0.25Qm25−0.10Qm10 }
- m1 =max{ m ∈ Z + ∪ { 0 } ∣ 0.01 Q m < = D i − 0.25 Q m 25 − 0.10 Q m 10 − 0.05 Q m 5 m\in Z^+ \cup \{0\} | 0.01Qm <= D_i-0.25Qm_{25}-0.10Qm_{10}-0.05Qm_{5} m∈Z+∪{0}∣0.01Qm<=Di−0.25Qm25−0.10Qm10−0.05Qm5 }
在实现过程中,对于需求超过车辆容量的客户必须进行需求拆分,而对于未超过车辆容量的客户可以拆分也可以不拆分,这里设置了参数比例进行限制。
3. 求解结果
(1)收敛曲线

(2)车辆路径

4. 代码片段
(1)数据结构
# 数据结构:解
class Sol():def __init__(self):self.node_no_seq = None # 节点id有序排列self.obj = None # 目标函数self.fitness = None # 适应度self.route_list = None # 车辆路径集合self.route_distance_list = None # 车辆路径长度集合
# 数据结构:网络节点
class Node():def __init__(self):self.id = 0 # 节点idself.x_coord = 0 # 节点平面横坐标self.y_coord = 0 # 节点平面纵坐标self.demand = 0 # 节点需求
# 数据结构:全局参数
class Model():def __init__(self):self.best_sol = None # 全局最优解self.demand_id_list = [] # 需求节点集合self.demand_dict = {}self.sol_list = [] # 解的集合self.depot = None # 车场节点self.number_of_demands = 0 # 需求节点数量self.vehicle_cap = 0 # 车辆最大容量self.distance_matrix = {} # 节点距离矩阵self.demand_id_list_ = [] # 经先验需求分割后的节点集合self.demand_dict_ = {} # 需求分割后的节点需求集合self.distance_matrix_ = {} # 原始节点id间的距离矩阵self.mapping = {} # 需求分割前后的节点对应关系self.split_rate = 0.5 # 控制需求分割的比例(需求超出车辆容量的除外)self.popsize = 100 # 种群规模self.Cr=0.5 # 差分交叉概率self.F=0.5 # 差分变异概率
(2)距离矩阵
# 初始化参数
def cal_distance_matrix(model):for i in model.demand_id_list:for j in model.demand_id_list:d=math.sqrt((model.demand_dict[i].x_coord-model.demand_dict[j].x_coord)**2+(model.demand_dict[i].y_coord-model.demand_dict[j].y_coord)**2)model.distance_matrix[i,j]=max(d,0.0001) if i != j else ddist = math.sqrt((model.demand_dict[i].x_coord - model.depot.x_coord) ** 2 + (model.demand_dict[i].y_coord - model.depot.y_coord) ** 2)model.distance_matrix[i, model.depot.id] = distmodel.distance_matrix[model.depot.id, i] = dist
(3)邻域
#差分变异;变异策略:DE/rand/1/bin
def muSol(model,v1):x1=model.sol_list[v1].node_no_seqwhile True:v2=random.randint(0,model.popsize-1)if v2!=v1:breakwhile True:v3=random.randint(0,model.popsize-1)if v3!=v2 and v3!=v1:breakx2=model.sol_list[v2].node_no_seqx3=model.sol_list[v3].node_no_seqmu_x=[min(int(x1[i]+model.F*(x2[i]-x3[i])),model.number_of_demands-1) for i in range(model.number_of_demands) ]return mu_x
#差分交叉
def crossSol(model,vx,vy):cro_x=[]for i in range(model.number_of_demands):if random.random()<model.Cr:cro_x.append(vy[i])else:cro_x.append(vx[i])cro_x=adjustRoutes(cro_x,model)return cro_x
参考
【1】 A novel approach to solve the split delivery vehicle routing problem
相关文章:

【进阶五】Python实现SDVRP(需求拆分)常见求解算法——差分进化算法(DE)
基于python语言,采用经典差分进化算法(DE)对 需求拆分车辆路径规划问题(SDVRP) 进行求解。 目录 往期优质资源1. 适用场景2. 代码调整3. 求解结果4. 代码片段参考 往期优质资源 经过一年多的创作,目前已经成…...
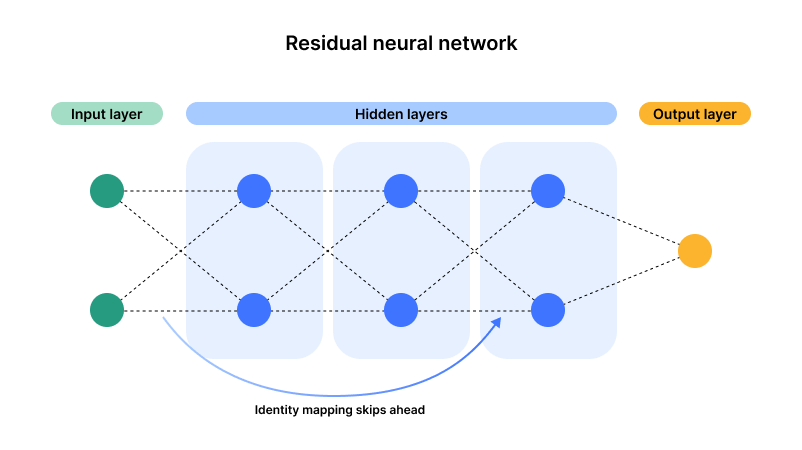
什么是神经网络?
一、什么是神经网络? 神经网络又称人工神经网络,是一种基于人脑功能模型的计算架构,因此称之为“神经”。神经网络由一组称为“节点”的处理单元组成。这些节点相互传递数据,就像大脑中的神经元相互传递电脉冲一样。 神经网络在…...

基于Python的图形用户界面设计及应用
基于Python的图形用户界面设计及应用 摘要:随着信息技术的飞速发展,图形用户界面(GUI)已成为现代软件不可或缺的一部分。Python作为一种简洁、易读且功能强大的编程语言,提供了多种GUI开发工具包,如Tkinte…...
python网络爬虫实战教学——urllib的使用(1)
文章目录 专栏导读1、前言2、urllib的使用3、发送请求3.1 urlopen3.2 request 专栏导读 ✍ 作者简介:i阿极,CSDN 数据分析领域优质创作者,专注于分享python数据分析领域知识。 ✍ 本文录入于《python网络爬虫实战教学》,本专栏针对…...

简述归并排序
归并排序 特点: 高效稳定时间复杂度最佳/平均/最差: O(N log N) 递归算法有专门的公式来计算时间复杂度 空间复杂度 O(N) 因为开辟了临时的tem_arr数组 一个静态的演示图(from leetcode) 一个动态的演示图 合并实现使用merge函数 inline void merge(v…...

HTML实现卷轴动画完整源码附注释
动画效果截图 页面的html结构代码 <!DOCTYPE html> <html> <head lang=...
sh: 1: dtc: not found
报错: bl31.bin size: 41632 u-boot-nodtb.bin size: 815816 ai_robot.dtb size: 30552 ./mkimage_uboot -E -p 0x3000 -f u-boot-ai-robot.its u-boot-ai-robot.itb sh: 1: dtc: not found ./mkimage_uboot: Cant open u-boot-ai-robot.itb.tmp: No such file …...

laravel 表单验证的 exists、unique 去除软删除字段的校验
use Illuminate\Validation\Rule; exists 去除软删除字段的校验 $validator \Validator::make($data, [phone_new > [Rule::exists(users, phone)->whereNull(deleted_at),]], [phone_new.exists > 手机号不存在,]);unique 去除软删除字段的校验 // 新增 email>r…...
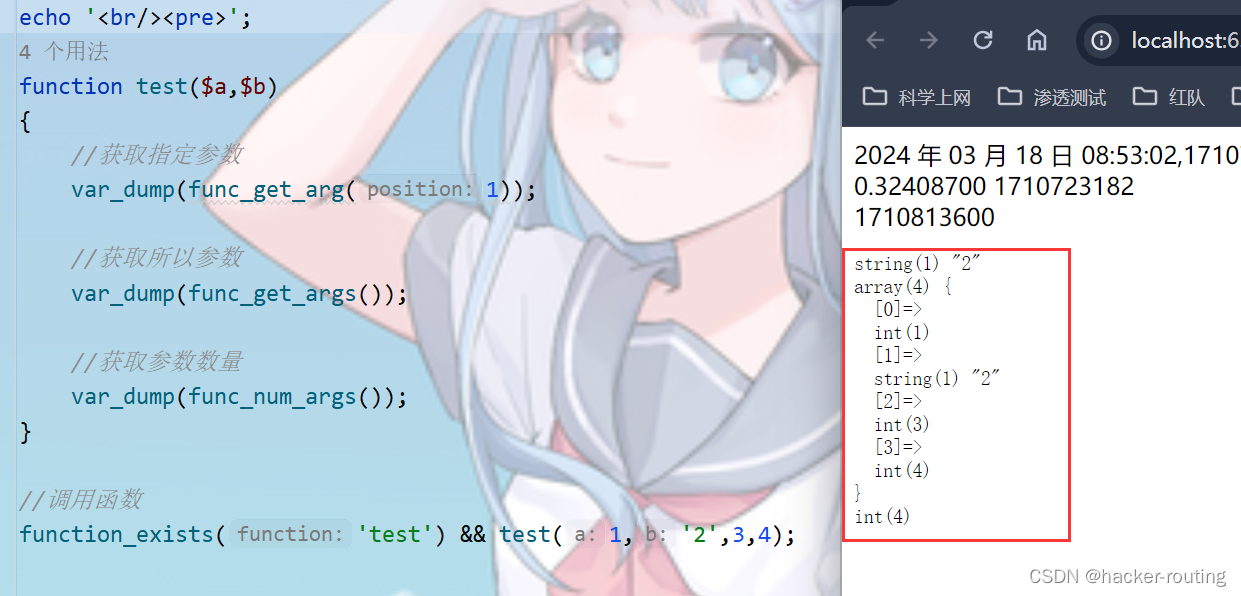
【PHP + 代码审计】函数详解2.0
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【Java、PHP】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收…...

宠物智能喂食机方案设计
我们都知道,现如今养宠物的人群已经很多了,主要是青年人居多,他们在独自漂泊的在外的工作,免不了情感泛滥,养一些小动物也是在预料之中。但由于工作或者其他各种因数,养宠人不可时时刻刻在家,对…...

测试直播打赏需要考虑哪些测试要点?
1.功能测试: 1、检查打赏功能是否正确 :检查打赏操作是否可以正常进行 2、 赞赏余额是否正确: 检查赞赏者和被赞赏者的余额是否正确 3、赞赏交易记录是否正确: 检查赞赏者和被赞赏者的交易记录是否正确; 4、检查赞…...
)
Python练习(续)
练习1:用户登录注册案例 import sysidname {test:123456}print(""" 英雄联盟商城登录界面~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~1. 用户登录2. 新用户注册3. 退出系统~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ …...
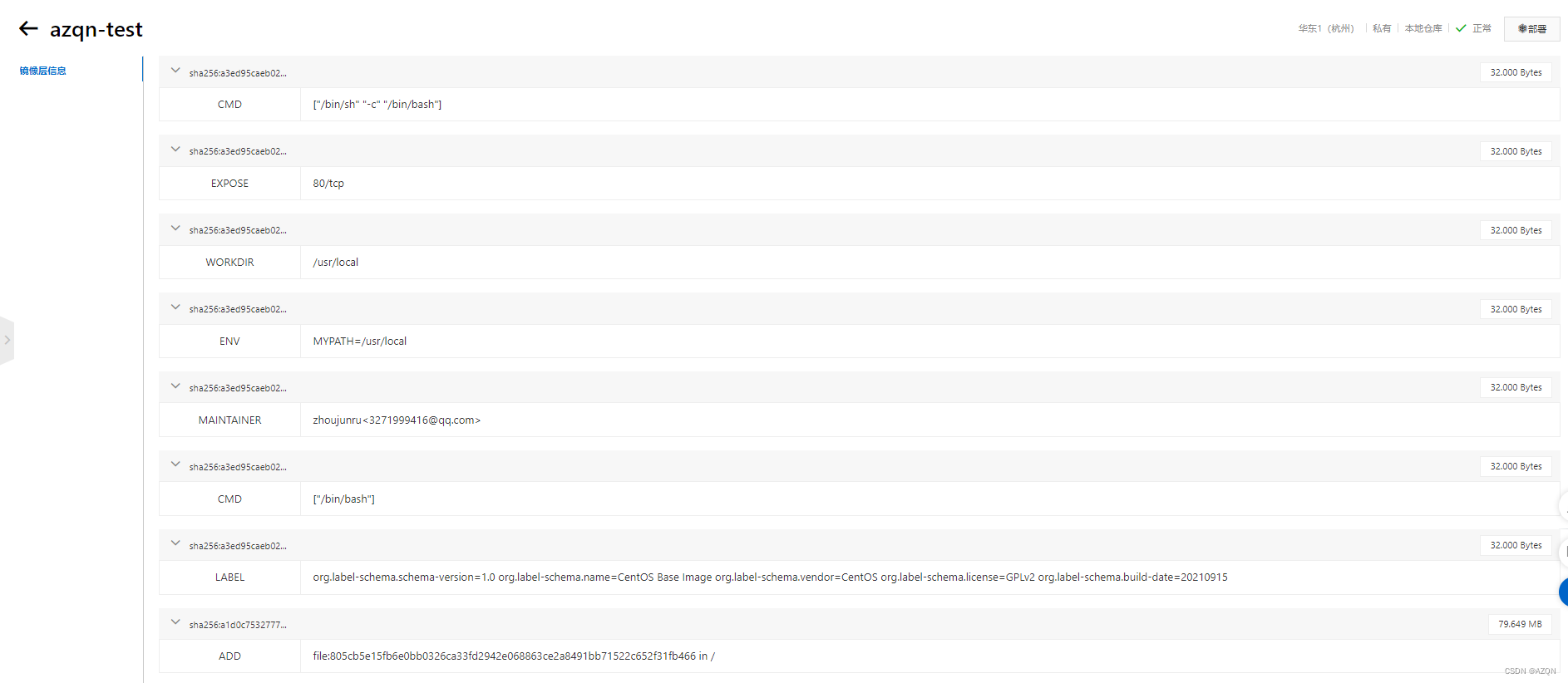
发布镜像到阿里云仓库
发布上一篇Dockerfile实战-自定义的centos镜像。 1、登录阿里云 2、找到容器镜像服务 3、创建命令空间 4、创建镜像仓库 5、点击进入这个镜像仓库,可以看到所有的信息 6、根据操作指南测试推送发布 6.1登录阿里云 [rootzhoujunru home]# docker login --usernam…...

web蓝桥杯真题:灯的颜色变化
代码及注释: // TODO:完善此函数 显示红色颜色的灯 function red() { //将红色图片元素display显示出来,其他隐藏document.querySelector(#defaultlight).style.display nonedocument.querySelector(#redlight).style.display inline-b…...
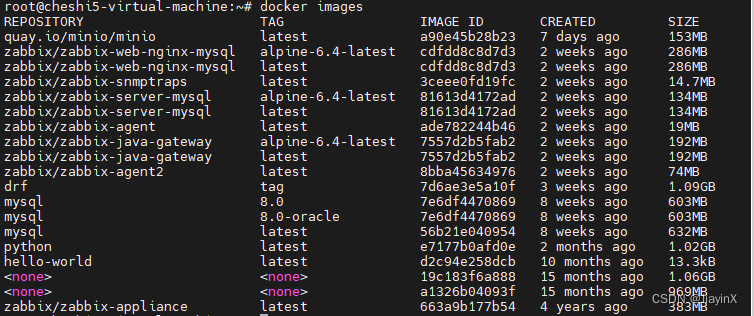
通过docker容器安装zabbix6.4.12图文详解(监控服务器docker容器)
目录 一、相关环境及镜像二、zabbix-server服务端部署1.使用docker创建zabbix-server服务端(1). 创建专用于Zabbix组件容器的网络(2). 启动空的MySQL服务器实例(3). 启动Zabbix Java网关实例(4). 启动Zabbix服务器实例并将实例与创建的MySQL服务器实例链接(5). 启动Zabbix Web界…...
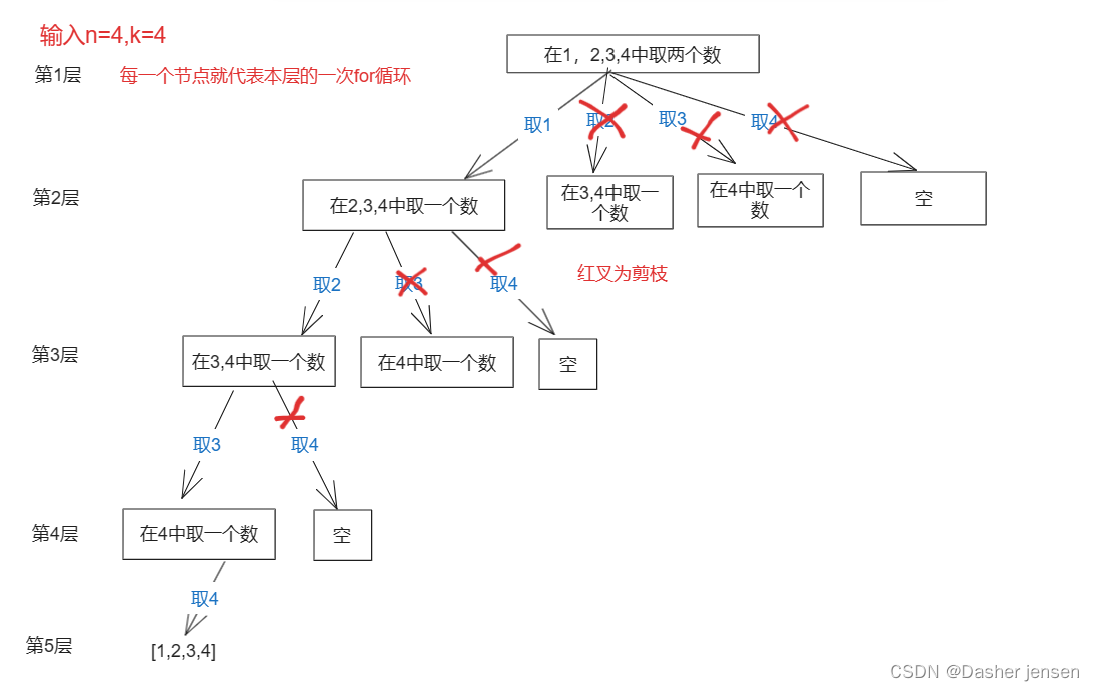
算法打卡day21|回溯法篇01|理论知识,Leetcode 77.组合
回溯法理论知识 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。所以回溯函数也就是递归函数,指的都是一个函数。 回溯法的效率 回溯法并不是什么高效的算法。因为回溯的本质是穷举,…...

C++ 输入输出
输入 1.1 cin >> str; 遇到“空格”、“TAB”、“回车”就停止 string str; cin >> str;1.2 getline(cin, str) 可用于输入一行数据,遇到空格不会停止,读入string字符中 便于读取一行一行的数据 while(getline(cin, str)){if(str "EN…...

FPGA高端项目:FPGA基于GS2971+GS2972架构的SDI视频收发+HLS图像缩放+多路视频拼接,提供4套工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐本博主所有FPGA工程项目-->汇总目录本博已有的 SDI 编解码方案本方案的SDI接收发送本方案的SDI接收图像缩放应用本方案的SDI接收纯verilog图像缩放纯verilog多路视频拼接应用本方案的SDI接收OSD动态字符叠加输出应用本方案的SDI接收HLS…...

【gpt实践】50个提升工作效率的GPT指令
收集整理了50个工作不同场景中可能会用到的gpt指令,希望对大家有帮助。 1. 用「532规则」定制月度宣传规划 提示:“对于我的 [产品/服务] 在 [社交媒体平台上 ]定位 [我的目标受众]”,使用 5-3-2 规则制定 1 个月的社交媒体内容计划。” Pro…...
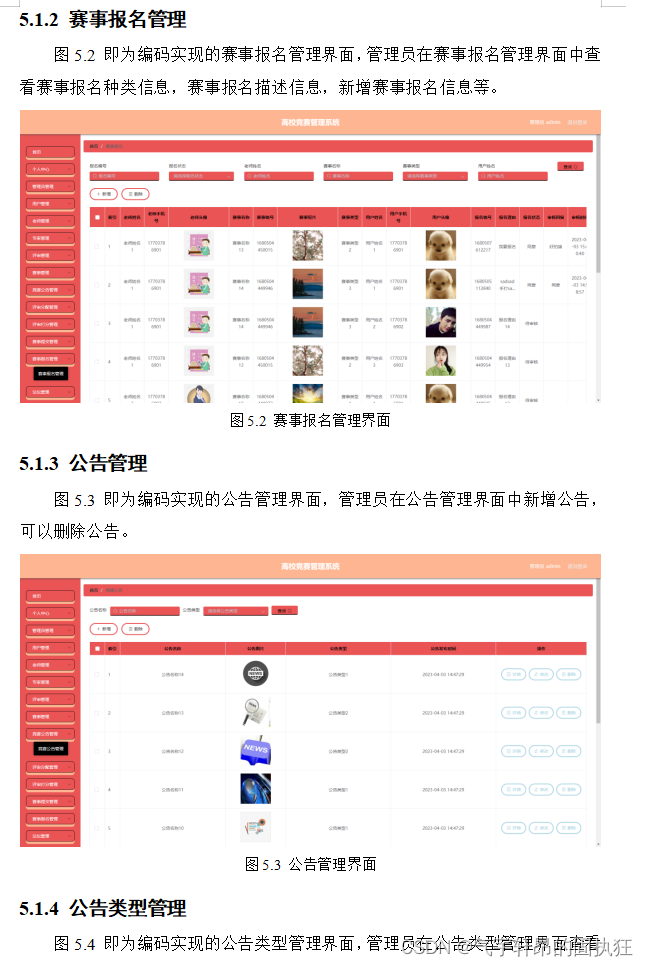
基于Springboot的高校竞赛管理系统(有报告)。Javaee项目,springboot项目。
演示视频: 基于Springboot的高校竞赛管理系统(有报告)。Javaee项目,springboot项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
