数据结构的概念大合集01(含数据结构的基本定义,算法及其描述)
概念大合集01
- 1、数据结构基础的定义
- 2、数据结构
- 2.1 数据元素之间关系的集合
- 2.2数据结构的三要素
- 2.2.1数据的逻辑结构
- 2.2.2数据的存储(物理)结构
- 2.2.3数据的运算
- 3、数据类型
- 4、抽象数据类型类型(ADT)
- 5、算法及其描述
- 5.1算法的5个特性
- 5.2算法设计的目标
- 5.3算法的时间复杂度
- 5.3.1时间复杂度的求和、求积定理
- 5.4算法的空间复杂度
阅读指导:
本文内容丰富,涵盖广泛,读者朋友们可以根据目录指引,直接跳跃至您感兴趣的章节开始品读。此外,作者正在积极创作后续篇章,如果您对本篇文章有所喜爱,不妨点击关注,以便第一时间获取最新作品动态。
现在,让我们开始正文的旅程吧。希望您能细细品味每一个字句,如果您在任何地方发现有任何不妥或欠缺之处,请在评论区不吝赐教。作者将虚心接受您的宝贵意见,并努力进行改进。期待您的宝贵反馈!
下一篇文章
数据结构的概念大合集02(线性表)
1、数据结构基础的定义
| 名称 | 具体概念 |
|---|---|
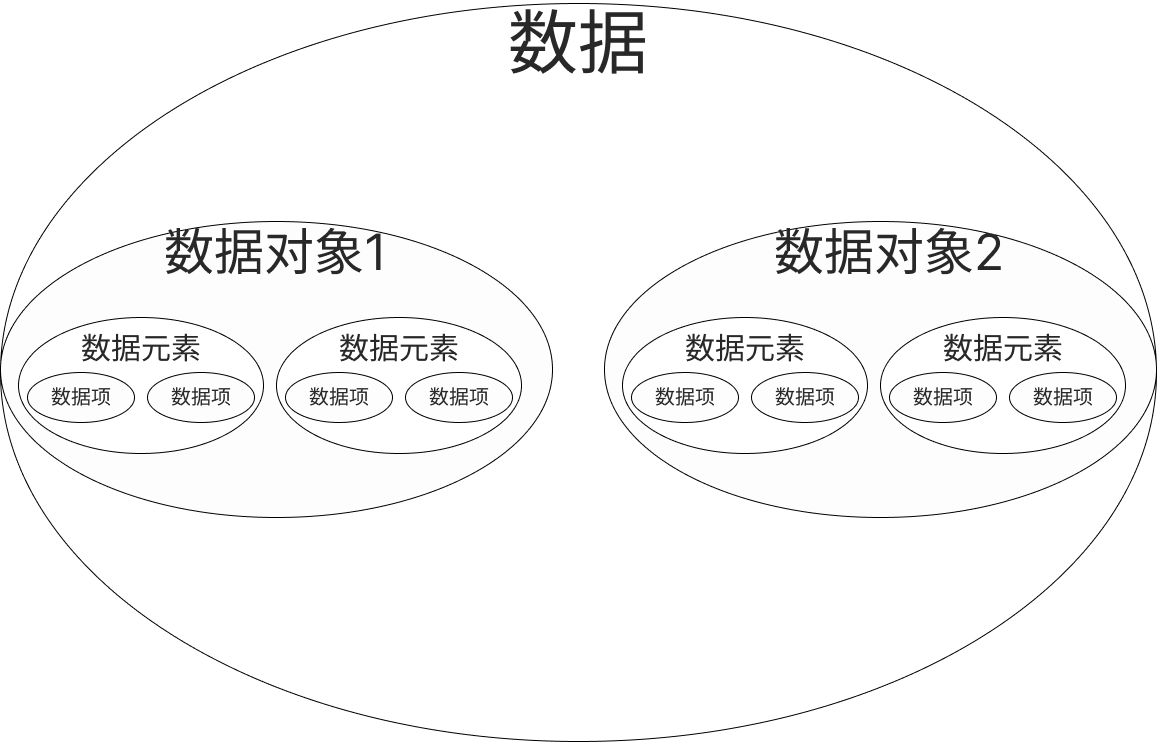
| 数据 | 描述客观事物的数和字符的集合,能被计算机程序处理的符号总称 |
| 数据元素 | 数据的基本单位,又称元素、结点、顶点、记录 |
| 数据项 | 是具有独立含义的数据最小单位,是构成数据元素的最小单位,又称字段、域 |
| 数据对象 | 性质相同的数据元素的集合,是数据的一个子集 |
| 数据结构 | 是相互之间存在一种或多种特定关系的数据元素的集合,包括逻辑结构和物理结构 |
| 数据类型 | 是一个值的集合和定义在这个值集上的一组操作的总称 |
| 抽象数据类型 | 是指一个数学模型以及定义在该模型上的一组操作 |
2、数据结构
2.1 数据元素之间关系的集合
| 数据的基本结构 | 关系 |
|---|---|
| 集合 | 属于同一个集合,没有什么具体关系 |
| 线性结构 | 一对一 |
| 树形结构 | 一对多 |
| 图形(网状)结构 | 多对多 |
2.2数据结构的三要素
2.2.1数据的逻辑结构
从逻辑上表示数据,与具体的存储无关
2.2.2数据的存储(物理)结构
指的是数据的逻辑结构在计算机的具体实现,依赖于计算机语言
2.2.3数据的运算
数据的运算包括运算定义和运算实现
- 运算定义:对于运算功能的描述,是抽象的,是基于逻辑关系的
- 运算实现:是程序员完成运算的实现算法,是具体的,是基于存储结构的
3、数据类型
指的是一组性质相同的值的集合和定义在此集合上的一组操作的总称
比如C语言中的int、float等。
4、抽象数据类型类型(ADT)
逻辑结构+抽象运算
定义抽象数据类型:
ADT 抽象数据类型名
{
数据对象:<数据对象的定义>
数据关系:<数据关系的定义>
基本操作:<基本操作的定义>
}
5、算法及其描述
5.1算法的5个特性
又穷性;确定性;可行性;有输入;有输出
5.2算法设计的目标
正确性;可使用性;可读性;健壮性;高效率与低存储量需求
5.3算法的时间复杂度
主要衡量的是一个算法的运行速度。为了描述一个算法的时间复杂度,人们发明了一个通用的表示方法:
「 大O符号表示法 」,即 T(n) = O(f(n))
我们先来看个例子:
for(i=1; i<=n; ++i) //第一行
{j = i; //第三行j++; //第四行
}
在大O符号表示法中,f(n)表示每行代码的执行次数之和;
所以上述代码中,第一行执行一次,第三行执行n次,第四行执行n次,整段代码执行(1+2n)次,即f(n)=1+2n;
取波极限,当n无穷大时,则令f(n)=n(注意不是2n,这是简化的写法);
于是此时T(n) = O(n);
为什么可以大O表示法可以简写呢,主要是因为这个表达式主要是表示代码执行时间的增长的变化趋势的,所以当n无穷大时,常数1和倍数2的意义就不是很大了。所以在采取大O表示法的时候,我们常取其指数最大的一项来表示,同时省略其他项和指数最大项的倍数。
常见的时间复杂度量级有:
- 常数阶O(1)
- 对数阶O(logN)
- 线性阶O(n)
- 线性对数阶O(nlogN)
- 平方阶O(n²)
- 立方阶O(n³)
- K次方阶O(n^k)
- 指数阶(2^n)
上面从上至下依次的时间复杂度越来越大,执行的效率越来越低。
5.3.1时间复杂度的求和、求积定理
T1(n) = O(f(n))
T2(n) = O(g(n))
求和:T1(n) + T2(n) = O( Max ( f(n),g(n) ) )
求积:T1(n) × T2(n) = O( f(n) × g(n) )
5.4算法的空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度,同样反映的是一个趋势,我们用 S(n) 来定义。与上面的时间复杂度一样,也采用大O表示法。
即S(n) = O( g(n) )
举例:
- 空间复杂度O(1)
如果算法执行所需要的临时空间不随着某个变量n的大小而变化,即此算法空间复杂度为一个常量,可表示为 O(1)
举例:
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;
代码中的 i、j、m 所分配的空间都不随着处理数据量变化,因此它的空间复杂度 S(n) = O(1)
- 空间复杂度O(n)
int fun(int n)
{return n < 2 ? n : fun(n - 1)*n;
}
阶乘递归函数会依次调用fun(N),fun(N-1),…,fun(2),fun(1),开辟了n个空间,所以空间复杂度为O(n) 。
相关文章:

数据结构的概念大合集01(含数据结构的基本定义,算法及其描述)
概念大合集01 1、数据结构基础的定义2、数据结构2.1 数据元素之间关系的集合2.2数据结构的三要素2.2.1数据的逻辑结构2.2.2数据的存储(物理)结构2.2.3数据的运算 3、数据类型4、抽象数据类型类型(ADT)5、算法及其描述5.1算法的5个…...
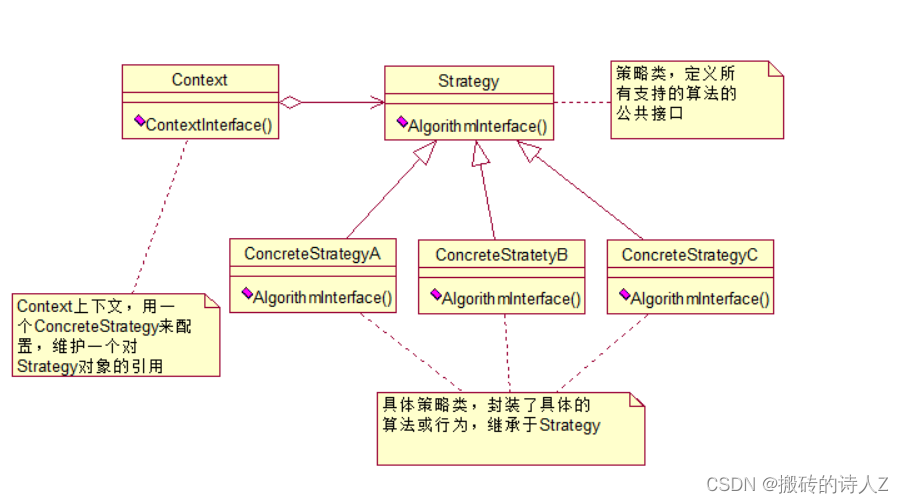
.NET高级面试指南专题十七【 策略模式模式介绍,允许在运行时选择算法的行为】
介绍: 策略模式是一种行为设计模式,它允许在运行时选择算法的行为。它定义了一系列算法,将每个算法封装到一个对象中,并使它们可以互相替换。这使得算法可独立于使用它的客户端变化。 原理: 策略接口(Strat…...

突飞猛进,智能饮品机器人如何助力实体经济?
近日,财务部公布了2024年第一季度及全年财报。数据显示,连锁品牌增长速度惊人,这其中不得不提到智能饮品机器人的使用,为不同的品牌门店拼速度、抢点位立下了不小的功劳,那么智能饮品机器人到底如何助力各门店…...
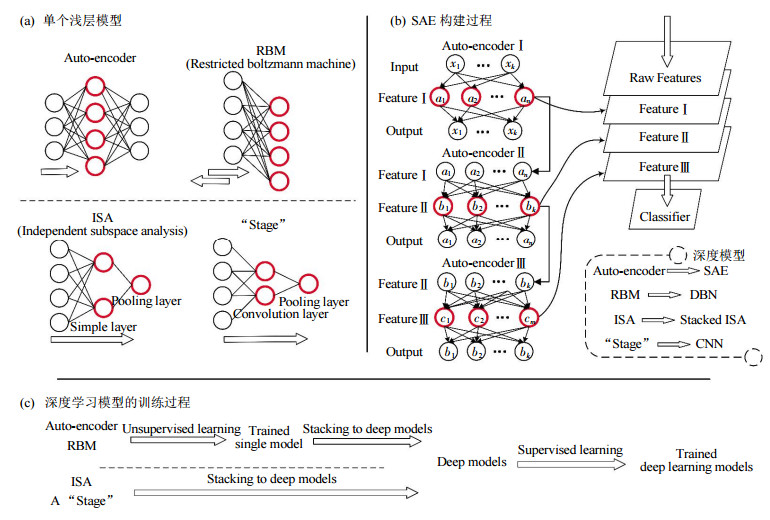
AI:150-基于深度学习的医学数据挖掘与病症关联发现
🚀点击这里跳转到本专栏,可查阅专栏顶置最新的指南宝典~ 🎉🎊🎉 你的技术旅程将在这里启航! 从基础到实践,深入学习。无论你是初学者还是经验丰富的老手,对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带关键代码,详细讲解供大家学习,希望…...

c语言:最大公约数
最大公约数 任务描述 最大公约数(也称最大公因数、最大公因子),指两个或多个整数共有约数中最大的一个。 编程输入两个正整数,输出它们的最大公约数。 输入示例 36 24输出示例 12代码 方法1:辗转相除法 #inclu…...

12 对称加密AES和非对称加密RSA
文章目录 一、对称加密算法AES1. AES简介2. AES代码 二、非对称加密RSA1. RSA简介2. 生成公钥私钥3. RSA代码 一、对称加密算法AES 1. AES简介 对称加密算法AES是目前广泛使用的一种加密技术,它采用相同的密钥来进行数据的加密和解密。 AES的优点 高效性&#x…...
:计算属性、监视属性、二者的区别)
Vue2(二):计算属性、监视属性、二者的区别
一、计算属性 1. 使用插值语法和methods拼接姓名 如果样式要求不多的话这样写没问题,如下代码是截取我输入的姓的前三个字母 <div id"root">姓:<input type"text" v-moudel"firstName">名:<…...
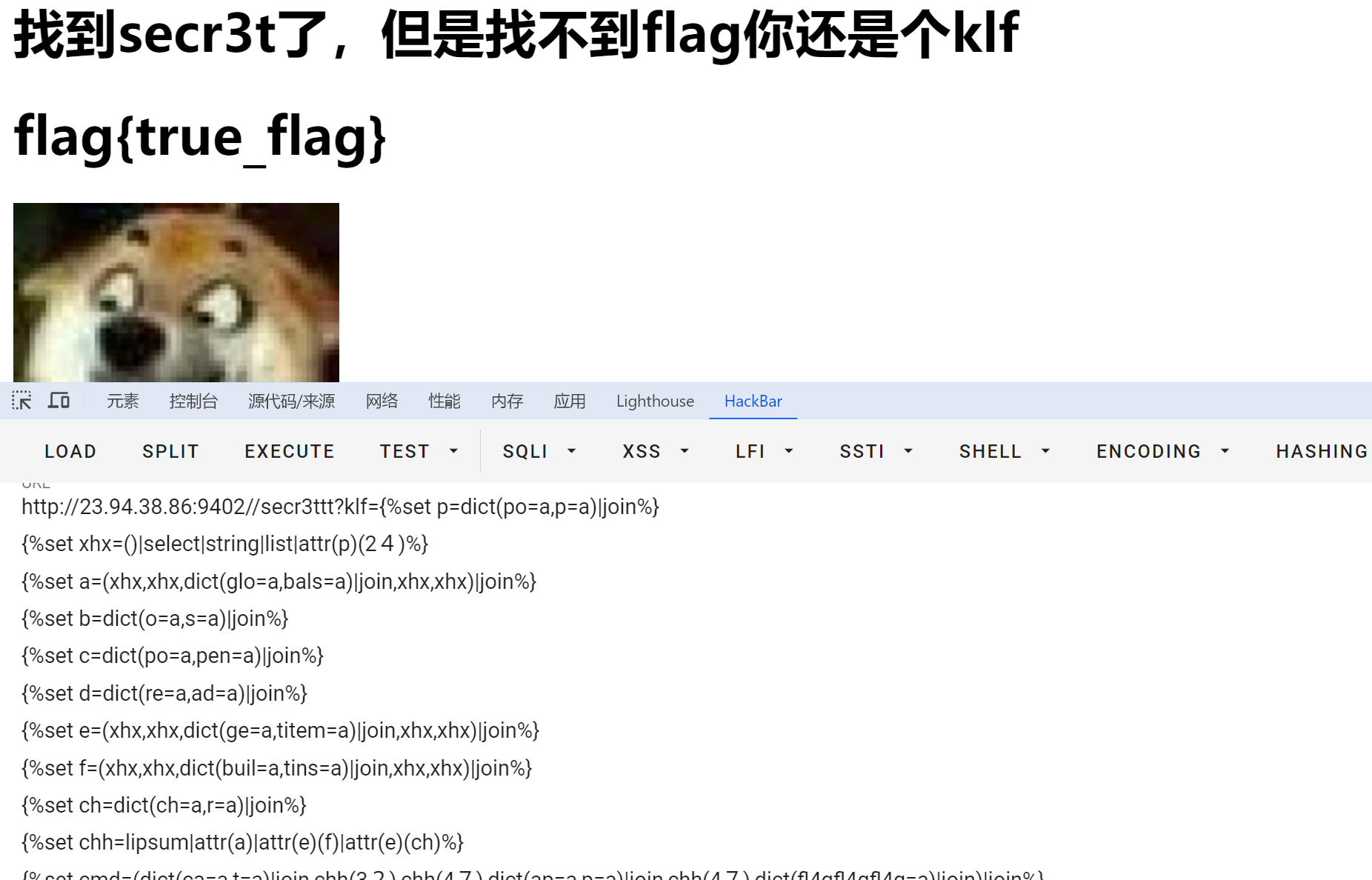
CTF题型 SSTI(2) Flask-SSTI典型题巩固
CTF题型 SSTI(2) Flask-SSTI典型题巩固 文章目录 CTF题型 SSTI(2) Flask-SSTI典型题巩固前记1.klf__sstiSSTI_Fuzz字典(网上收集自己补充) 2.klf_2数字问题如何解决了?|count |length都被禁? 3.klf_3 前记 从基础到自己构造paylo…...

计算机设计大赛 题目: 基于深度学习的疲劳驾驶检测 深度学习
文章目录 0 前言1 课题背景2 实现目标3 当前市面上疲劳驾驶检测的方法4 相关数据集5 基于头部姿态的驾驶疲劳检测5.1 如何确定疲劳状态5.2 算法步骤5.3 打瞌睡判断 6 基于CNN与SVM的疲劳检测方法6.1 网络结构6.2 疲劳图像分类训练6.3 训练结果 7 最后 0 前言 🔥 优…...
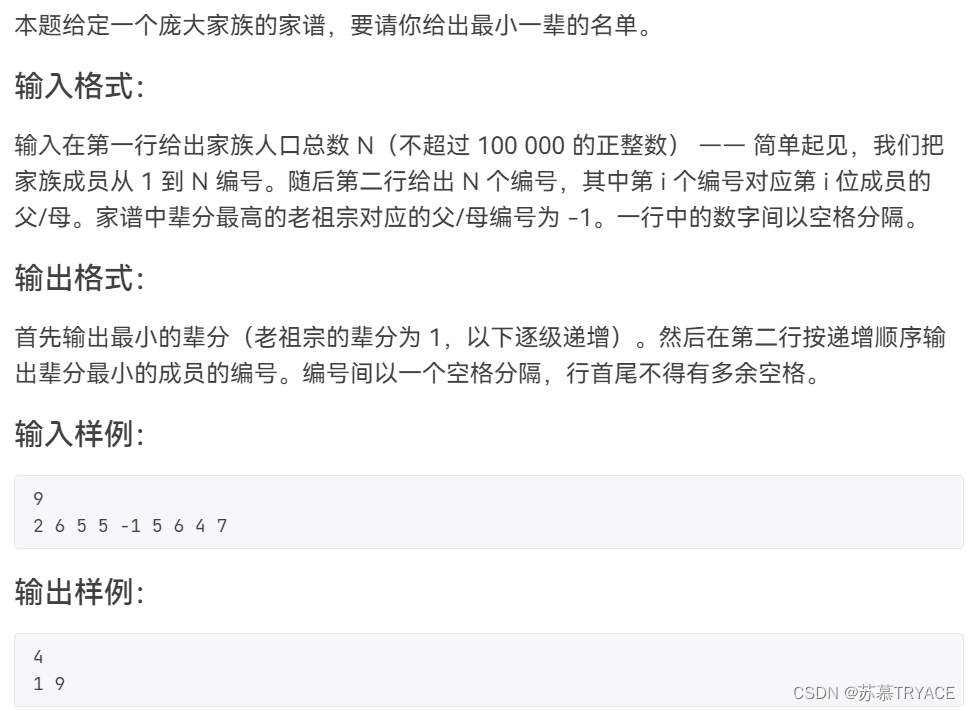
小字辈[天梯赛]
文章目录 题目描述思路AC代码 题目描述 思路 深度优先搜索 具体流程 1.读入每个人的祖先,标记辈分最高的老祖宗对应的下标pos 2.从pos开始dfs,每次判断当前遍历的深度,如果>原来的深度,更新,并将存储最小辈分的数组…...

Linux常用操作命令、端口、防火墙、磁盘与内存
目录 1.Linux常用操作命令 1.1 基本命令 1.2 高级命令 2.Linux防火墙 2.1 iptables 2.2 firewalld 3.Linux端口号 3.1 netstat(查看网络连接) 3.2 lsof(查找占用端口的进程) 3.3 ps(查看进程服务路径&#x…...
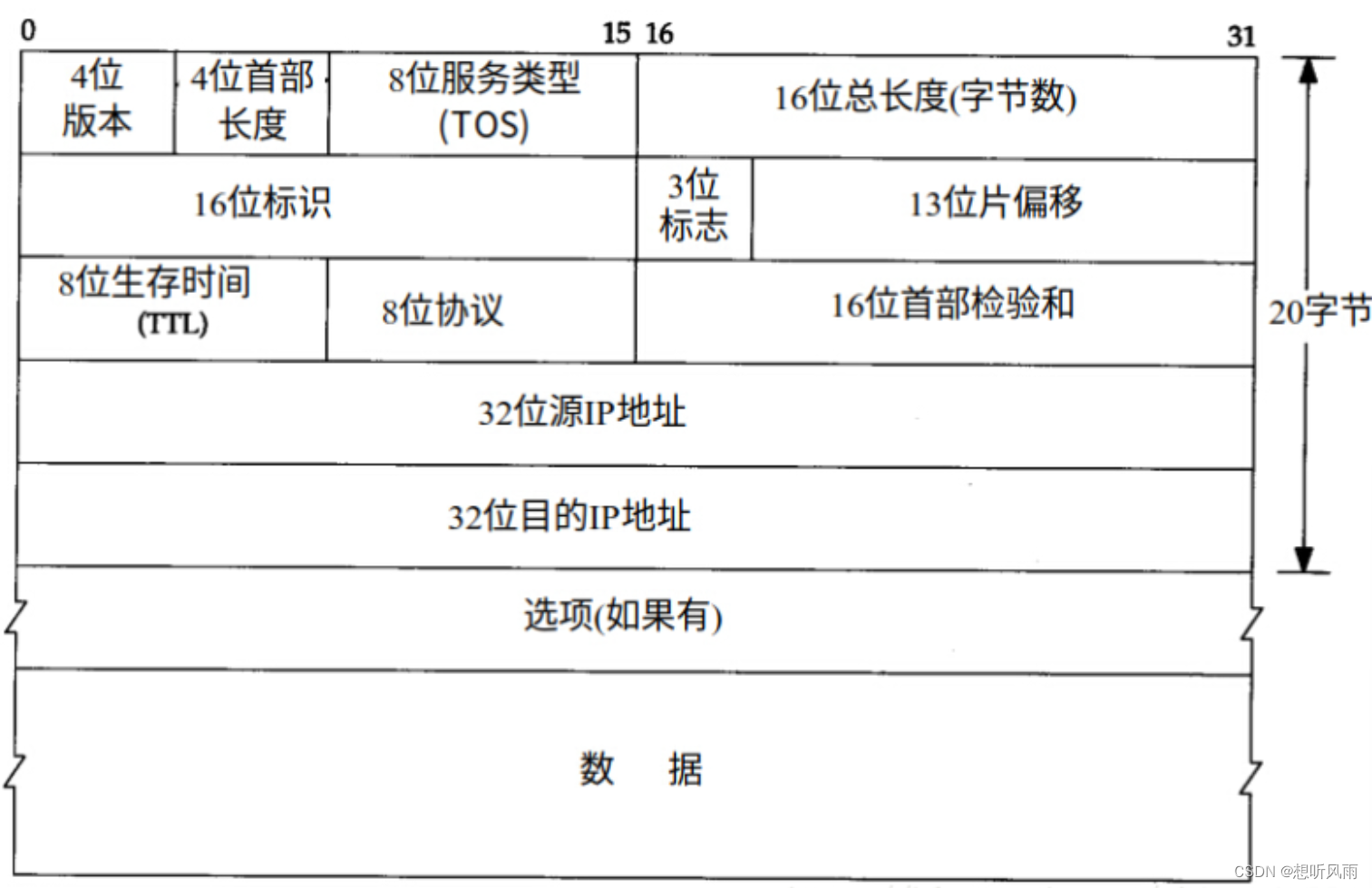
<JavaEE> 了解网络层协议 -- IP协议
目录 初识IP协议 什么是IP协议? IP协议中的基础概念 IP协议格式 图示 4bit版本号(version) 4bit头部长度(headerlength) 8bit服务类型(TypeOfService) 16bit总长度(total l…...
【安全类书籍-2】Web渗透测试:使用Kali Linux
目录 内容简介 作用 下载地址 内容简介 书籍的主要内容是指导读者如何运用Kali Linux这一专业的渗透测试平台对Web应用程序进行全面的安全测试。作者们从攻击者的视角出发,详细阐述了渗透测试的基本概念和技术,以及如何配置Kali Linux以适应渗透测试需求。书中不仅教授读者…...
ubuntu10.04 apache2.2开启tls1.2的支持,使现代的edge和firefox浏览器能正常访问https
最近发现自己ubuntu10.04服务器上的apache https无法通过win11上的edge和firefox浏览器访问,但xp下的ie6和ie8没有问题。 firefox的错误提示为“此网站可能不支持TLS 1.2协议,而这是Firefox支持的最低版本”。 经过检查发现: IE6访问https所需的版本是SS…...
算法学习(持续更新中)
学习视频:一周刷爆LeetCode,算法大神左神(左程云)耗时100天打造算法与数据结构基础到高级全家桶教程,直击BTAJ等一线大厂必问算法面试题真题详解(马士兵)_哔哩哔哩_bilibili 时间复杂度 一个操…...

蓝桥杯 2023 省B 飞机降落
首先,这题要求的数据量比较少,我们可以考虑考虑暴力解法。 这题可能难在很多情况的考虑,比如说: 现在时间是10,有个飞机20才到,我们是可以干等10分钟。 #include <iostream> #include <…...
基于python的变配电室运行状态评估与预警系统flask-django-nodejs-php
近年来,随着我国工业化、城镇化步伐的不断加快,城市配电网络取得令人瞩目的发展成果。变配电室是供配电系统的核心,在供配电系统中占有特殊的重要地位[1]。变配电室电气设备运行状态和环境信息缺乏必要的监测评估预警手段,如有一日遭遇突发情…...
,右键单击展示操作菜单,可编辑单元格高亮展示)
el-table左键双击单元格编辑内容(输入框输入计算公式可直接得出结果),右键单击展示操作菜单,可编辑单元格高亮展示
vue2点击左侧的树节点(el-tree)定位到对应右侧树形表格(el-table)的位置,树形表格懒加载 表格代码 <el-table ref"singleTable" :data"detailsList" highlight-current-row"" row-key"detailId"…...

实现HBase表和RDB表的转化(附Java源码资源)
实现HBase表和RDB表的转化 一、引入 转化为HBase表的三大来源:RDB Table、Client API、Files 如何构造通用性的代码模板实现向HBase表的转换,是一个值得考虑的问题。这篇文章着重讲解RDB表向HBase表的转换。 首先,我们需要分别构造rdb和hba…...

10:00面试,10:06就出来了,问的问题有点变态。。。
从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天必不可少的,看在钱给的比较多的份上,就不太计较了。没想到8月一纸通知,所有人不准加班,加班费不仅没有了,薪资还要降40%…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
