【动态规划】【同余前缀和】【多重背包】[推荐]2902. 和带限制的子多重集合的数目
本文涉及知识点
动态规划汇总
C++算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频
C++算法:滑动窗口总结
多重背包
LeetCode2902. 和带限制的子多重集合的数目
给你一个下标从 0 开始的非负整数数组 nums 和两个整数 l 和 r 。
请你返回 nums 中子多重集合的和在闭区间 [l, r] 之间的 子多重集合的数目 。
由于答案可能很大,请你将答案对 109 + 7 取余后返回。
子多重集合 指的是从数组中选出一些元素构成的 无序 集合,每个元素 x 出现的次数可以是 0, 1, …, occ[x] 次,其中 occ[x] 是元素 x 在数组中的出现次数。
注意:
如果两个子多重集合中的元素排序后一模一样,那么它们两个是相同的 子多重集合 。
空 集合的和是 0 。
示例 1:
输入:nums = [1,2,2,3], l = 6, r = 6
输出:1
解释:唯一和为 6 的子集合是 {1, 2, 3} 。
示例 2:
输入:nums = [2,1,4,2,7], l = 1, r = 5
输出:7
解释:和在闭区间 [1, 5] 之间的子多重集合为 {1} ,{2} ,{4} ,{2, 2} ,{1, 2} ,{1, 4} 和 {1, 2, 2} 。
示例 3:
输入:nums = [1,2,1,3,5,2], l = 3, r = 5
输出:9
解释:和在闭区间 [3, 5] 之间的子多重集合为 {3} ,{5} ,{1, 2} ,{1, 3} ,{2, 2} ,{2, 3} ,{1, 1, 2} ,{1, 1, 3} 和 {1, 2, 2} 。
提示:
1 <= nums.length <= 2 * 104
0 <= nums[i] <= 2 * 104
nums 的和不超过 2 * 104 。
0 <= l <= r <= 2 * 104
动态规划
vCnt[i]记录i在nums中出现的次数,vCnt[i]不为0的数目不超过200个。
子多重集合 就是子序列。
i为0要特殊处理,否则会死循环。
动态规划的状态表示
dp[i][j] 表示 ,从[0,i]中选取若干个数和为j的可能数。状态数:O(200r)。
注意用滚动向量vPre、dp实现。
由于unorder_map 大约是O(10),所以有超时的风险。直接vector<vector<>> 空间复杂度是:O(nr),空间会超。
利用前缀和优化转移方程
计算后置状态:
dp[j] = ∑ x : 0 v C n t [ i ] v P r e [ j − x × i ] s . t j − x × i > = 0 \Large\sum_{x:0}^{vCnt[i]}vPre[j-x\times i] \quad s.t \quad j-x \times i>=0 ∑x:0vCnt[i]vPre[j−x×i]s.tj−x×i>=0
显然,可以用前缀和优化。
转移方程的时间复杂度为:O(1),总时间复杂度为O(200r)。
动态规划的填表顺序
i从大到小。从小到大似乎也没问题。
动态规划的初始值
vPre[0]=1
动态规划的范围值
∑ x : l r v P r e [ x ] \Large \sum _{x:l}^r vPre[x] ∑x:lrvPre[x]
代码
核心代码
template<int MOD = 1000000007>
class C1097Int
{
public:C1097Int(long long llData = 0) :m_iData(llData% MOD){}C1097Int operator+(const C1097Int& o)const{return C1097Int(((long long)m_iData + o.m_iData) % MOD);}C1097Int& operator+=(const C1097Int& o){m_iData = ((long long)m_iData + o.m_iData) % MOD;return *this;}C1097Int& operator-=(const C1097Int& o){m_iData = (m_iData + MOD - o.m_iData) % MOD;return *this;}C1097Int operator-(const C1097Int& o){return C1097Int((m_iData + MOD - o.m_iData) % MOD);}C1097Int operator*(const C1097Int& o)const{return((long long)m_iData * o.m_iData) % MOD;}C1097Int& operator*=(const C1097Int& o){m_iData = ((long long)m_iData * o.m_iData) % MOD;return *this;}bool operator<(const C1097Int& o)const{return m_iData < o.m_iData;}C1097Int pow(long long n)const{C1097Int iRet = 1, iCur = *this;while (n){if (n & 1){iRet *= iCur;}iCur *= iCur;n >>= 1;}return iRet;}C1097Int PowNegative1()const{return pow(MOD - 2);}int ToInt()const{return m_iData;}
private:int m_iData = 0;;
};class Solution {
public:int countSubMultisets(vector<int>& nums, int left, int r) {const int iMax = *std::max_element(nums.begin(), nums.end());vector<int> vCnt(1 + iMax);for (const auto& n : nums){vCnt[n]++;}vector<C1097Int<>> vPre(r + 1);vPre[0] = 1;for (int i = iMax; i >= 0; i--){if (0 == vCnt[i]){continue;}vector<C1097Int<>> dp(r + 1);if (0 == i){for (int k = 0; k <= r; k++){dp[k] = vPre[k] * (1 + vCnt[i]);}}else{for (int m = 0; m < i; m++){C1097Int<> iiSum = 0;for (int k = m; k <= r; k += i){iiSum += vPre[k];const int delIndex = k - (vCnt[i] + 1) * i;if (delIndex >= 0){iiSum -= vPre[delIndex];}dp[k] = iiSum;}}}vPre.swap(dp);}C1097Int<> biRet = std::accumulate ( vPre.begin() + left, vPre.begin() + r + 1, C1097Int<>());return biRet.ToInt();}
};
测试用例
emplate<class T, class T2>
void Assert(const T& t1, const T2& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{vector<int> nums;int l, r;{Solution sln;nums = { 1, 2, 2, 3 }, l = 6, r = 6;auto res = sln.countSubMultisets(nums, l, r);Assert(1, res);}{Solution sln;nums = { 2, 1, 4, 2, 7 }, l = 1, r = 5;auto res = sln.countSubMultisets(nums, l, r);Assert(7, res);}{Solution sln;nums = { 1, 2, 1, 3, 5, 2 }, l = 3, r = 5;auto res = sln.countSubMultisets(nums, l, r);Assert(9, res);}
}
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划】【同余前缀和】【多重背包】[推荐]2902. 和带限制的子多重集合的数目
本文涉及知识点 动态规划汇总 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 C算法:滑动窗口总结 多重背包 LeetCode2902. 和带限制的子多重集合的数目 给你一个下标从 0 开始的非负整数数组 nums 和两个整数 l 和 r 。 请你…...

nginx介绍及搭建
架构模型 Nginx是由一个master管理进程、多个worker进程组成的多进程模型。master负责管理worker进程,worker进程负责处理网络事件,整个框架被设计为一种依赖事件驱动、异步、非阻塞的模式。 优势: 1、充分利用多核,增强并发处理…...

树莓派夜视摄像头拍摄红外LED灯
NoIR相机是一种特殊类型的红外摄像头,其名称来源于"No Infrared"的缩写。与普通的彩色摄像头不同,NoIR相机具备红外摄影和低光条件下摄影的能力。 一般摄像头能够感知可见光,并用于普通摄影和视频拍摄。而NoIR相机则在设计上去除了…...

Oracle19C静默安装教程
文章目录 一、安装前的准备1、安装Linux操作系统2、配置网络源或者本地源3、hosts文件配置 二、准备安装环境1、安装依赖包2、创建oracle用户组3、配置系统内核参数4、关闭selinux5、配置oracle用户环境6、修改用户的Shell限制 三、静默安装Oracle数据库1、创建oracle安装目录2…...
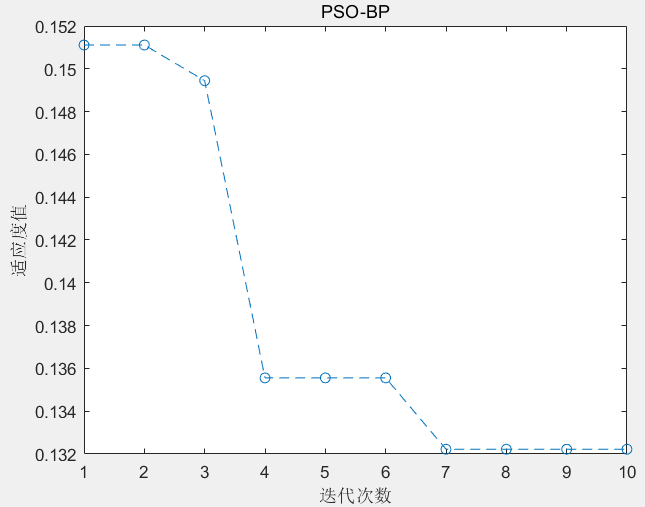
【机器学习】基于粒子群算法优化的BP神经网络分类预测(PSO-BP)
目录 1.原理与思路2.设计与实现3.结果预测4.代码获取 1.原理与思路 【智能算法应用】智能算法优化BP神经网络思路【智能算法】粒子群算法(PSO)原理及实现 2.设计与实现 数据集: 多输入多输出:样本特征24,标签类别4…...

Sora后时代文生视频的探索
一、写在前面 按常理,这里应该长篇大论地介绍一下Sora发布对各行业各方面产生的影响。不过,这类文章已经很多了,我们今天主要聊聊那些已经成熟的解决方案、那些已经可以“信手拈来”的成果,并以此为基础,看看Sora发布…...

指南:在各主流操作系统上安装与配置Apache Tomcat
指南:在各主流操作系统上安装与配置Apache Tomcat Apache Tomcat作为一款广受欢迎的开源Java Servlet容器,为用户提供了一个纯Java环境下的Web服务器和Servlet容器。本文将详细介绍如何在不同的操作系统上安装Apache Tomcat,并进行基本的配置…...

物联网的介绍
物联网(Internet of Things,简称IoT)是指通过互联网将物理设备、传感器、通信设备和软件系统相互连接,形成一个网络化的系统。它可以实现设备之间的数据交换、信息共享和远程控制,使得物理世界与数字世界紧密结合。 物…...
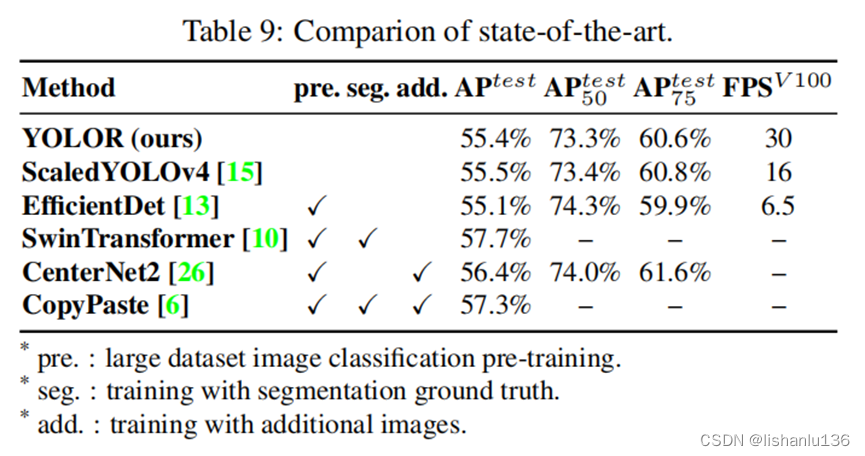
目标检测——YOLOR算法解读
论文:YOLOR-You Only Learn One Representation: Unifified Network for Multiple Tasks 作者:Chien-Yao Wang, I-Hau Yeh, Hong-Yuan Mark Liao 链接:https://arxiv.org/abs/2105.04206 代码:https://github.com/WongKinYiu/yolo…...

NVIDIA NCCL 源码学习(十三)- IB SHARP
背景 之前我们看到了基于ring和tree的两种allreduce算法,对于ring allreduce,一块数据在reduce scatter阶段需要经过所有的rank,allgather阶段又需要经过所有rank;对于tree allreduce,一块数据数据在reduce阶段要上行…...
Spark-Scala语言实战(4)
在之前的文章中,我们学习了如何在scala中定义无参,带参以及匿名函数。想了解的朋友可以查看这篇文章。同时,希望我的文章能帮助到你,如果觉得我的文章写的不错,请留下你宝贵的点赞,谢谢。 Spark-Scala语言…...

ffmpeg不常用命令整理
最近做了许多有关音视频方面的工作,接触了一些不常用的命令,整理分享出来。 1.剪辑视频 ffmpeg -ss 1 -to 4 -accurate_seek -i input.mp4 -c:v copy output.mp4指定从视频中的第1秒开始,到第4秒结束的部分剪辑。 ss:指定开始时…...
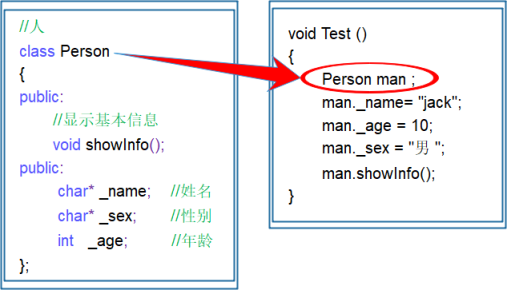
怎么理解面向对象?一文带你全面理解
文章目录 1、类和对象(1)面向过程和面向对象初步认识(2)类的引入(3)类的定义(4)类的访问限定符及封装4.1 访问限定符4.2 封装 (5)类的作用域(6&am…...
神经网络(深度学习,计算机视觉,得分函数,损失函数,前向传播,反向传播,激活函数)
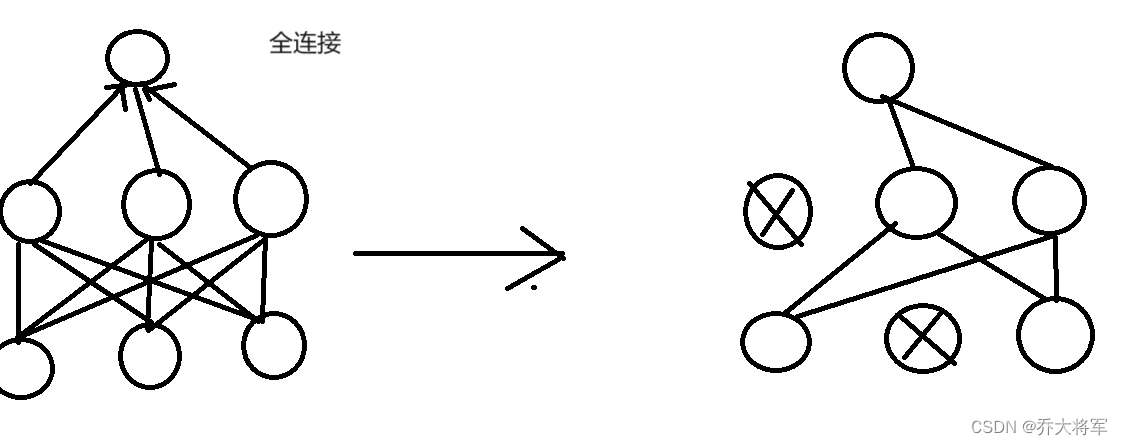
目录 一、神经网络简介 二、深度学习要解决的问题 三、深度学习的应用 四、计算机视觉 五、计算机视觉面临的挑战 六、得分函数 七、损失函数 八、前向传播 九、反向传播 十、神经元的个数对结果的影响 十一、正则化与激活函数 一、神经网络简介 神经网络是一种有监督…...

Tomcat的Host Manager页面403的原因和解决办法
目录 背景 原因: 解决方案 背景 一直报错 403 Access Denied You are not authorized to view this page.By default the Host Manager is only accessible from a browser running on the same machine as Tomcat. If you wish to modify this restriction, youll need to…...

零基础学华为ip认证难吗?华为认证费用多少?
零基础学华为ip认证难吗? 首先,零基础的学习者可以通过系统的学习,逐步掌握网络基础知识和技能。可以通过阅读教材、参加培训课程、进行实践操作等方式,不断提升自己的知识和技能水平。同时,学习者还可以利用华为提供的…...

[C语言]——内存函数
目录 一.memcpy使用和模拟实现(内存拷贝) 二.memmove 使用和模拟实现 三.memset 函数的使用(内存设置) 四.memcmp 函数的使用 C语言中规定: memcpy拷贝的就是不重叠的内存memmove拷贝的就是重叠的内存但是在VS202…...

QGIS编译(跨平台编译)056:PDAL编译(Windows、Linux、MacOS环境下编译)
点击查看专栏目录 文章目录 1、PDAL介绍2、PDAL下载3、Windows下编译4、linux下编译5、MacOS下编译1、PDAL介绍 PDAL(Point Data Abstraction Library)是一个开源的地理空间数据处理库,它专注于点云数据的获取、处理和分析。PDAL 提供了丰富的工具和库,用于处理激光扫描仪、…...

计算机三级——网络技术(综合题第二题)
路由器工作模式 用户模式 当通过Console或Telnet方式登录到路由器时,只要输入的密码正确,路由器就直接进入了用户模式。在该模式下,系统提示符为一个尖括号(>)。如果用户以前为路由器输入过名称,则该名称将会显示在尖指号的前…...

Python 深度学习第二版(GPT 重译)(二)
四、入门神经网络:分类和回归 本章涵盖 您的第一个真实世界机器学习工作流示例 处理矢量数据上的分类问题 处理矢量数据上的连续回归问题 本章旨在帮助您开始使用神经网络解决实际问题。您将巩固从第二章和第三章中获得的知识,并将所学应用于三个新…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
