理解树的结构-算法通关村
理解树的结构-算法通关村
1.树的结构
- 树是一个有n个有限节点组成一个具有层次关系的集合,每个节点有0个或者多个子节点,没有父节点的节点称为根节点,也就是说除了根节点以外每个节点都有父节点,并且有且只有一个。树的种类比较多,最常见的是二又树,基本结构如下:
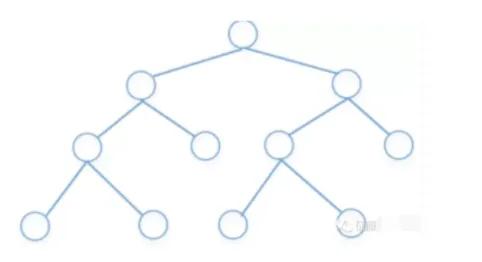
- 参考上面的结构,可以很方便的理解树的如下概念:
- 节点的度:一个节点含有的子节点的个数称为该节点的度;
- 树的度:一棵树中,最大的节点的度称为树的度,注意与节点度的区别;
- 叶节点或终端节点:度为0的节点称为叶节点;
- 非终端节点或分支节点:度不为0的节点;
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
- 有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树;
- 二叉树:每个节点最多含有两个子树的树称为二叉树;
2 树的性质
- 性质1:在二叉树的第i层上至多有2^(i-1)个结点(i>0)
性质2:深度为k的二叉树至多有2^k -1个结点(k>0)
性质3:对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1;
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
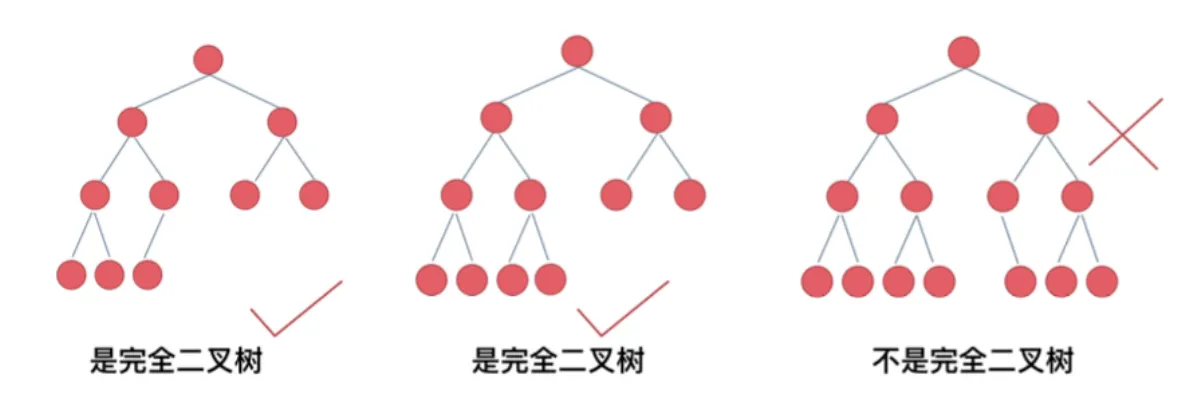
性质5:对完全二叉树,若从上至下、从左至右编号,则编号为i的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2(i=1 时为根,除外) - 满二叉树就是如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树。

- 这棵二又树为满二叉树,也可以说深度为k=4,有2^k-1=15个节点的二又树。完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大 值,并且最下面一层的节点都集中在该层最左边的若干位置。
3 树的定义
-
定义二叉树
-
public class TreeNode {int val;TreeNode left;TreeNode right;} -
定义N叉树
-
public class Node {public int val;public List<Node> children;}
4树的遍历方式
- 二叉树的遍历方式有层次遍历和深度优先遍历两种:
• 深度优先遍历:先往深走,遇到叶子节点再往回走。
•广度优先遍历:一层一层的去遍历,一层访问完再访问下一层。
这两种遍历方式不仅仅是二叉树,N树叉也有这两种方式的,图结构也有,只不过我们更习惯叫广度优先和深度优先,本质是一回事。
深度优先又有前中后序三种,记住一点:前指的是中间的父节点在遍历中的顺序,只要大家记住前中后序指的就是父节点在访问中的顺序就可以了。
前序遍历:中左右 中序遍历:左中右 后序遍历:左右中 
5 通过序列构造二叉树
- 前面我们已经介绍了前中后序遍历的基本过程,现在我们看一下如何通过给出的序列来恢复原始二叉树,看三个序列:
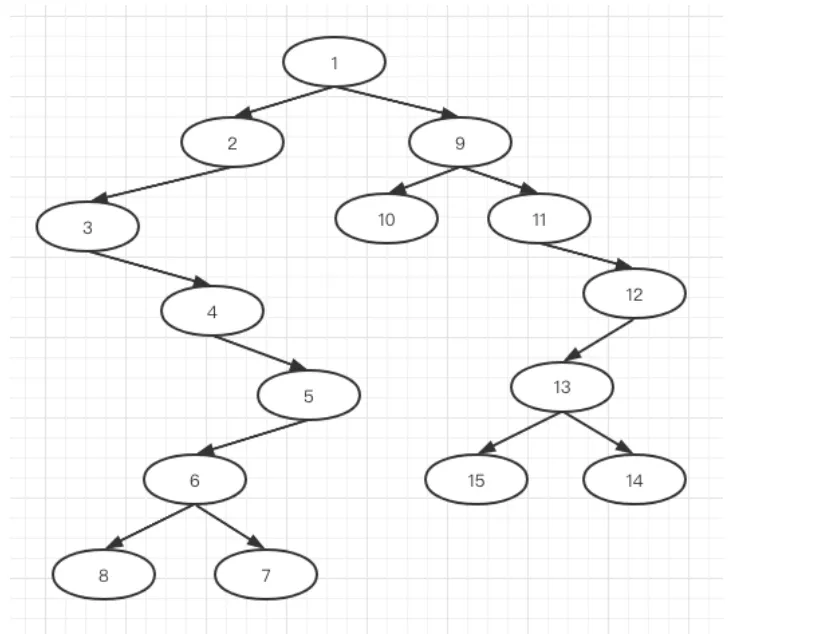
(1)前序:1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2)中序:3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
(3) 后序:8 7 6 5 4 3 2 10 15 14 13 12 11 9 1
5.1前中序列复原二叉树
-
先看如何通过前中序列复原二叉树:
-
(1)前序:1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2)中序:3 4 8 6 7 5 2 1 10 9 11 15 13 14 12 -
第一轮 -
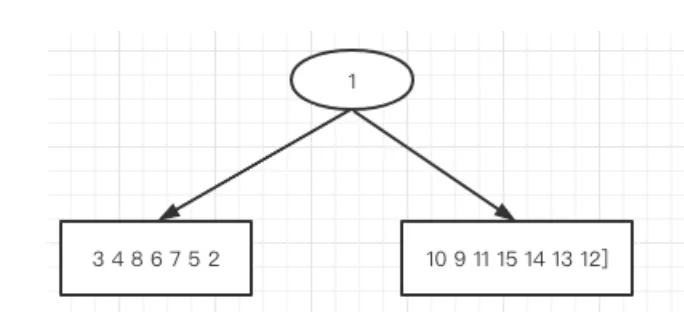
我们知道前序第一个访问的就是根节点,所以根节点就是1。
中序遍历的特点是根节点的左子树的元素都在根节点的左侧,右子树的元素都在根节点的右侧,从中序遍历序列我们可以划分成如下结构: -
前序中序划分: 中序序列划分:[3 4 8 6 7 5 2 ] 1 [10 9 11 15 13 14 12] 前序序列划分:1 [2 3 4 5 6 8 7] [9 10 11 12 13 15 14] -
上面前序序列第一个括号里的都是左子树的元素,第二个括号一定都是右子树的元素。参照中序的两个数组划分的。我们看到前序中7之前的元素都在中序第一个数组中,9之后的所有元素就在第二个数组种,所以我们从7和9之间划分。
由此,画图表示一下此时知道的树的结构为: -
-
第二轮 -
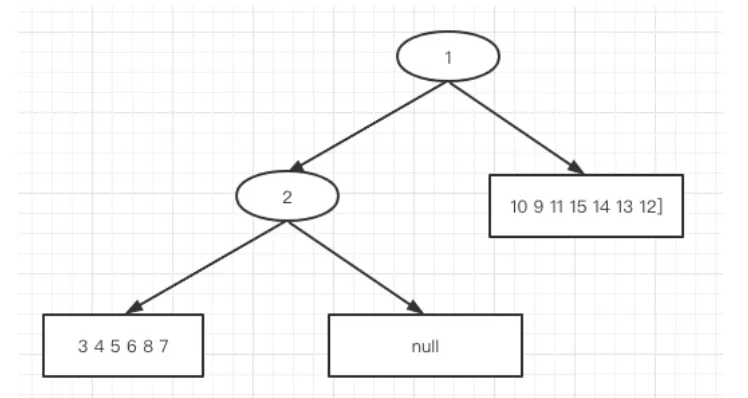
我们先看两个序列的第一个数组:
前序:2 3 4 5 6 8 7 中序:3 4 8 6 7 5 2
此时又可以利用上面的结论划分了:根节点是2,然后根据2在中序中的位置可以划分为: -
序列 前序: 2 [3 4 5 6 8 7] 中序:[3 4 8 6 7 5 ] 2 -
此时树的结构为:
-
-
第三轮: -
对 3 4 5 6 8 7 继续划分 : 前序:3 [4 5 6 8 7] 中序:3 [ 4 8 6 7 5 ] 此时结构为:
-
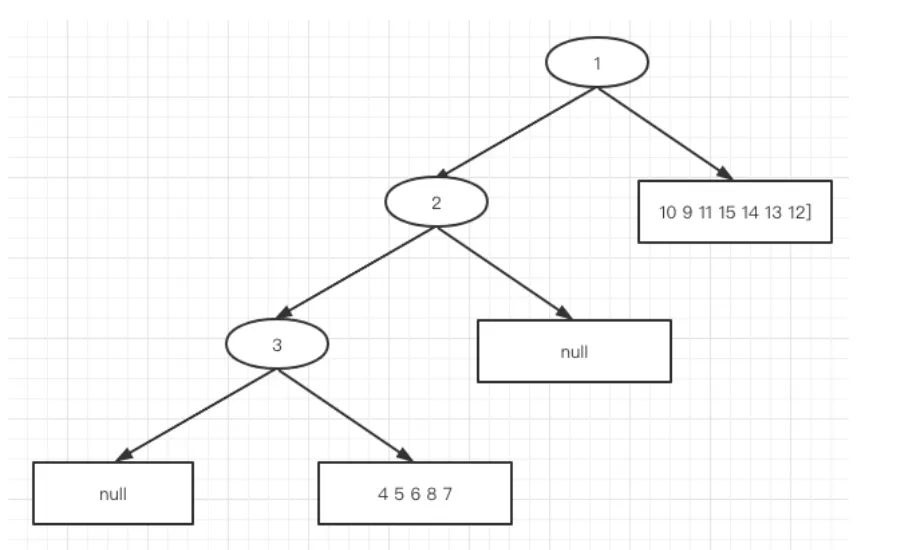
-
第四轮 -
对 4 5 6 8 7 继续划分:前序: 4 [5 6 8 7 ] 中序:4 [8 6 7 5 ]
-

-
第五轮: -
对 5 6 8 7 继续划分:前序:5 [6 8 7 ] 中序:[8 6 7] 5
-

-
同理,对序列 [10 9 11 15 13 14 12],进行划分:
-
5.2 通过中序和后序序列恢复二叉树
- 通过中序和后序也能恢复原始序列的,唯一的不同是后序序列的最后一个是根节点,中序的处理也是上面一样的过程:
前序:12345687910 1112 1315 14
中序: 3486752110911 15 13 14 12
后序:876543210 15 14 13 12 1191
可以自行试一试,不再赘述。
问题:为什么前序和后序不能恢复二叉树
既然上面两种都行,那为什么前序和后序不行呢?我们看上面的例子:
(1) 前序: 123456879 10 1112 13 15 14
(2) 后序:87654321015 141312 1191
后序:876543210 15 14 13 12 1191
可以自行试一试,不再赘述。
问题:为什么前序和后序不能恢复二叉树
既然上面两种都行,那为什么前序和后序不行呢?我们看上面的例子:
(1) 前序: 123456879 10 1112 13 15 14
(2) 后序:87654321015 141312 1191 - 根据上面的说明,我们通过前序可以知道根节点是1,通过后序也能知道根节点是1,但是中间是怎么划分的呢?其他元素哪些属于左子树,哪些属于右子树呢?很明显通过两个序列都不知道,所以前序和后序序列不能恢复二叉树。
相关文章:

理解树的结构-算法通关村
理解树的结构-算法通关村 1.树的结构 树是一个有n个有限节点组成一个具有层次关系的集合,每个节点有0个或者多个子节点,没有父节点的节点称为根节点,也就是说除了根节点以外每个节点都有父节点,并且有且只有一个。树的种类比较多…...
金融知识分享系列之:支撑阻力
金融知识分享系列之:支撑阻力 一、支撑阻力原理二、支撑阻力作用1.识别市场资金的预期2.作为入场和平仓的重要参考 三、寻找支撑阻力四、延伸思考五、支撑阻力总结 一、支撑阻力原理 支撑阻力核心要素: 锚定效应订单驱动 支撑阻力原理: 市…...
如何使用Excel创建一个物品采购表
在企业的日常运营中,物品采购是一个常见且重要的活动。有效的采购管理不仅可以确保企业及时获得所需物资,还可以控制成本、提高效率。Microsoft Excel是一个功能强大的工具,它可以帮助我们创建和管理物品采购表。本文将详细介绍如何使用Excel…...

容器中的大模型(三)| 利用大语言模型:容器化高效地部署 PDF 解析器实践...
作者:宋文欣,智领云科技联合创始人兼CTO 01 简介 大语言模型(LLMs)正逐渐成为人工智能领域的一颗璀璨明星,它们的强大之处在于能够理解和生成自然语言,为各种应用提供了无限可能。为了让这些模型更好地服务…...

java采集小程序联合航空官方
本文仅限学习研究讨论,切忌做非法乱纪之事 中国联合航空有限公司(以下简称“中国联合航空”)总部位于北京,现为中国东方航空股份有限公司(以下简称“东航”)旗下的全资子公司。中国联合航空成立于1986年12月26日&#…...
)
【力扣每日一题】lc1793. 好子数组的最大分数(单调栈)
LC1793. 好子数组的最大分数 题目描述 给你一个整数数组 nums (下标从 0 开始)和一个整数 k 。 一个子数组 (i, j) 的 分数 定义为 min(nums[i], nums[i1], ..., nums[j]) * (j - i 1) 。 一个 好 子数组的两个端点下标需要满足 i < k < j 。 请…...

ES的集群节点发现故障排除指南(1)
本文是ES官方文档关于集群节点发现与互联互通的问题排查指南内容。 英文原文(官网) 集群节点发现是首要任务 集群互连,重中之重! 在大多数情况下,发现和选举过程会迅速完成,并且主节点会长时间保持当选状…...

使用html+css制作一个发光立方体特效
使用htmlcss制作一个发光立方体特效 <!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>Documen…...

贵州省二级分类土地利用数据(矢量)
贵州省,地处中国西南腹地,地貌属于中国西南部高原山地,境内地势西高东低,自中部向北、东、南三面倾斜,平均海拔在1100米左右。贵州高原山地居多,素有“八山一水一分田”之说。全省地貌可概括分为࿱…...
通过nginx+xray服务搭建及本地配置
一、xray服务配置 下载:https://github.com/XTLS/Xray-core 进入下载界面 这里我选择的是Xray-linux-64.zip 将文件解压到 /usr/local/xray 编辑配置文件/usr/local/xray/config.json uuid可以在v2ray客服端自动生成,也可以在UUID v4 生成器 - KKT…...
第一节 Axure RP产品经理原型进阶学习
第一天 1、认识RP9 Axure RP 9,Axure RP 9是美国 Axure Software Solution公司的旗舰产品, 是一个快速的原型工具,常用于各项网络设计,包括了原型图、线框图等等。 要进行原型设计,将文字性文档转变为互动性的可视画…...
 文件压缩)
Linux实战笔记(三) 文件压缩
大家好,我是半虹,这篇文章来讲 Linux 系统中常用的文件压缩方式 0、序言 在 Linux 系统中,存在许多打包或压缩文件的工具 这篇文章会对一些常用的工具进行分类整理和介绍 如果只是需要知道怎么对不同格式的文件做解压缩,可以直…...

树形递归模板
详情参考CSDN链接: https://www.cnblogs.com/lidar/p/12972792.html public class Menu {// 菜单idprivate String id;// 菜单名称private String name;// 父菜单idprivate String parentId;// 菜单urlprivate String url;// 菜单图标private String icon;// 菜单顺序private …...

Python实战:Pandas数据合并与重塑
本文将深入探讨Pandas库在数据合并与重塑方面的强大功能。我们将涵盖多种数据合并方法,如merge、join、concat等,以及数据重塑的技巧,如pivot_table、merge_asof等。 一、引言 Pandas是一个强大的Python数据分析库,它提供了丰富…...
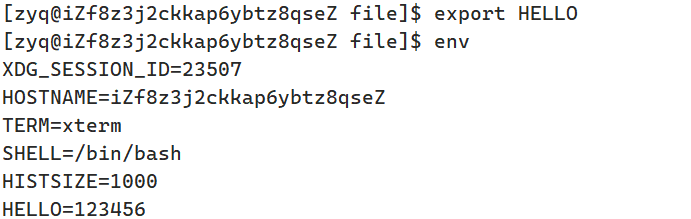
如何理解 Linux 命令行参数与环境变量7
一、命令行参数 1.1参数介绍 在写C语言程序时,main函数是否可以带参数呢?------ 是可以的 int argc: 命令行参数的个数char *argv[ ]: 字符指针数组(指向各个命令行参数的字符指针所构成的数组) 我们写一段代码来打印一下看这…...

奥特曼回应GPT5
欢迎再次与大家会面!在积累了大量的信息和趋势后,今天我们将深入了解 Sora、OpenAI 董事会、以及近期与其有关的所有声讨。我们将直接跳入与 OpenAI 首席执行官 Sam Altman 的深度访谈,探讨从 AGI 到 GPT-5 的未来,以及 Sam 对人工…...
QT----给程序添加上任务栏托盘图标和退出
让我们的程序拥有任务栏托盘图标,实现程序后台运行,退出等功能 1、关闭程序保持后台 重写关闭事件,忽略点击窗口关闭 void MainWindow::closeEvent(QCloseEvent *event) {// 隐藏窗口,而不是真正关闭setVisible(false);// 忽略关闭事件&am…...

arm地址对齐的总结
static void axi_azx_writeb(u8 value, u8 __iomem *addr) { u32 data; u32 offset; offset (u64)addr & 0x03; // 编译器不允许地址做& 操作时要强转为数据 addr (u8 __iomem *)((u64)addr & 0xFFFFFFFFFFFFFFFC); // __iomem是个64位的地址 u8表示从这个地址…...
就业班 2401--3.13 走进网络
走进网络 长风破浪会有时,直挂云帆济沧海。 1.认识计算机 1.计算机网络是由计算机和通讯构成的,网络研究的是“通信”。 ------1946 世界上第一台计算机 2.终端:只有输入和输出功能,没有计算和处理功能。 3.数据:一串…...
)
SWIFT介绍和学习(简单入门级别)
SWIFT介绍和学习 SWIFT功能介绍SWIFT快速使用LLM及LLM最佳实践(LLM系列文章)部署指南 vllm非官方介绍资料 项目地址:https://github.com/modelscope/swift 任何有疑惑的地方,参考项目首页readme寻求答案 SWIFT功能介绍 SWIFT&…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...

比特币:固若金汤的数字堡垒与它的四道防线
第一道防线:机密信函——无法破解的哈希加密 将每一笔比特币交易比作一封在堡垒内部传递的机密信函。 解释“哈希”(Hashing)就是一种军事级的加密术(SHA-256),能将信函内容(交易细节…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...
本地部署drawDB结合内网穿透技术实现数据库远程管控方案
文章目录 前言1. Windows本地部署DrawDB2. 安装Cpolar内网穿透3. 实现公网访问DrawDB4. 固定DrawDB公网地址 前言 在数字化浪潮席卷全球的背景下,数据治理能力正日益成为构建现代企业核心竞争力的关键因素。无论是全球500强企业的数据中枢系统,还是初创…...
