线性代数在卷积神经网络(CNN)中的体现
案例:深度学习中的卷积神经网络(CNN)
在图像识别领域,卷积神经网络(Convolutional Neural Networks, CNN)是一个广泛应用深度学习模型,它在人脸识别、物体识别、医学图像分析等方面取得了显著成效。CNN中的核心操作——卷积,就是一个直接体现线性代数应用的例子。
假设我们正在训练一个用于识别猫和狗的图像分类器,原始输入是一幅RGB彩色图片,可以将其视为一个高度、宽度和通道数(RGB)的三维矩阵。当我们应用一个卷积核(滤波器)到输入图像上时,实际上是进行了一次二维卷积运算,该运算可以理解为一个小型矩阵(卷积核)与输入图像在空间域上的加权求和,这就是线性代数中的矩阵乘法和卷积运算的直观体现。
具体步骤如下:
1. 卷积核(Filter)是一个小的矩阵,它的元素代表着权重,当它与图像矩阵相乘时,实际上是在做局部特征检测。比如,一个检测边缘特征的卷积核可能在图像的某一部分产生较大的响应值,这是因为该部分图像满足了边缘检测的特征。
2. 在卷积过程中,卷积核在图像上滑动,每次滑动都会产生一个新的输出值,这个过程相当于在做矩阵乘法的逐元素操作(Element-wise multiplication)和累加(Summation),即进行了一系列的线性变换。
3. 通过多次卷积层的叠加,CNN能够提取出图像的多层次特征,并逐渐抽象出高级特征,这些特征最终被送入全连接层进行分类。这里的全连接层本质上也是一个线性模型,其权重矩阵反映了输入特征与输出类别的线性关系。
所以,在这个案例中,线性代数不仅体现在卷积层的卷积运算上,还在全连接层的权重矩阵定义了输入特征到输出标签的线性映射,这些都是深度学习模型中不可或缺的组成部分,也是线性代数在人工智能应用中的直接体现。
相关文章:
中的体现)
线性代数在卷积神经网络(CNN)中的体现
案例:深度学习中的卷积神经网络(CNN) 在图像识别领域,卷积神经网络(Convolutional Neural Networks, CNN)是一个广泛应用深度学习模型,它在人脸识别、物体识别、医学图像分析等方面取得…...

服务器根据用途划分有哪几种?
随着企业需求的不同,服务器的类型也变得多种多样了,有根据机箱结构来划分的服务器类型,如机架式服务器、刀片式服务器和塔式服务器等,也有按照应用层次来划分的服务器类型,如入门级服务器和工作组服务器等。 那根据用途…...

linux 命令笔记:gpustat
1 命令介绍 gpustat是一个基于Python的命令行工具,它提供了一种快速、简洁的方式来查看GPU的状态和使用情况它是nvidia-smi工具的一个封装,旨在以更友好和易于阅读的格式显示GPU信息。gpustat不仅显示基本的GPU状态(如温度、GPU利用率和内存…...
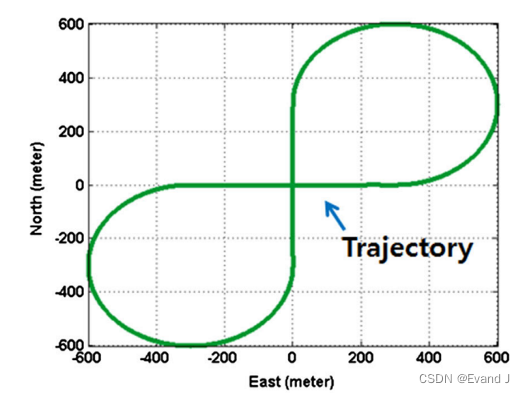
【阅读笔记】Adaptive GPS/INS integration for relative navigation
Lee J Y, Kim H S, Choi K H, et al. Adaptive GPS/INS integration for relative navigation[J]. Gps Solutions, 2016, 20: 63-75. 用于相对导航的自适应GPS/INS集成 名词翻译 formation flying:编队飞行 摘要翻译 在编队飞行、防撞、协同定位和事故监测等许多…...
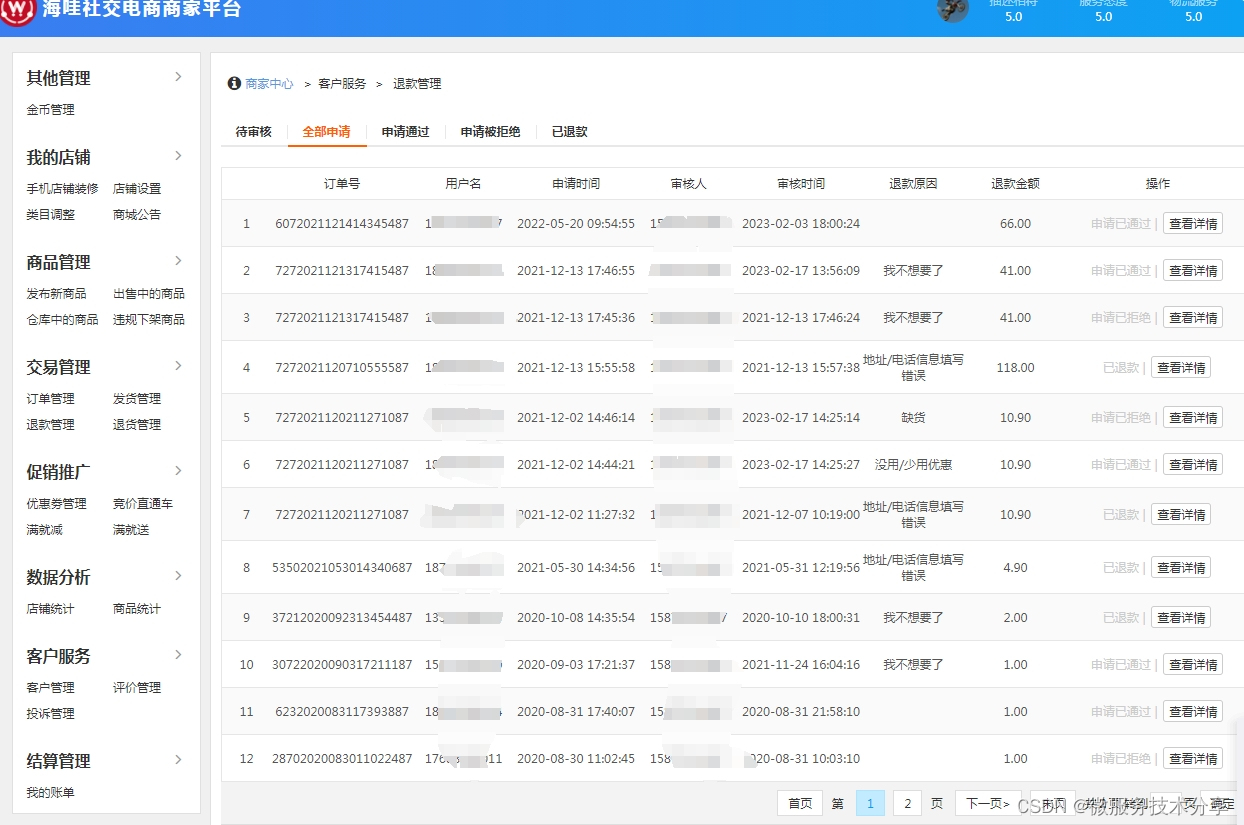
Java版直播商城免 费 搭 建:电商、小程序、三级分销及免 费 搭 建,平台规划与营销策略全掌握
随着互联网的快速发展,越来越多的企业开始注重数字化转型,以提升自身的竞争力和运营效率。在这个背景下,鸿鹄云商SAAS云产品应运而生,为企业提供了一种简单、高效、安全的数字化解决方案。 鸿鹄云商SAAS云产品是一种基于云计算的软…...

经典Bug永流传---每周一“虫”(四十五)
如果有人错过机会,多半不是机会没来,而是因为机会过来时,没有一伸手抓住它。 大写W惹的祸 前提: A账号已登录 步骤: 打开某商品链接,然后在商品的评论区任意一条评论,点击回复,回…...
蓝桥杯-礼物-二分查找
题目 思路 --刚开始想到暴力尝试的方法,但是N太大了,第一个测试点都超时。题目中说前k个石头的和还有后k个石头的和要小于s,在这里要能想到开一个数组来求前n个石头的总重,然后求前k个的直接将sum[i]-sum[i-k-1]就行了࿰…...

设计原则、工厂、单例模式
什么是设计模式 简单来说,设计模式就是很多程序员经过相当长的一段时间的代码实践、踩坑所总结出来的一套解决方案,这个解决方案能让我们少写一些屎山代码,能让我们写出来的代码写出来更加优雅,更加可靠。所以设计模式的好处是显而…...

笔记:Mysql 主从搭建
主库 创建用户并授权 create user slave identified with mysql_native_password by 123456 GRANT REPLICATION SLAVE ON *.* to slave%; FLUSH PRIVILEGES;主库配置文件 /etc/my.cnf #日志路径及文件名,目录要是mysql有权限写入 log-bin/var/lib/mysql/binlog …...

HTTP Error 400. The request hostname is invalid.
异常信息 <!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01//EN""http://www.w3.org/TR/html4/strict.dtd"> <HTML><HEAD><TITLE>Bad Request</TITLE> <META HTTP-EQUIV"Content-Type" Content"text/html;…...
)
mysql日志( Redo Log 、Undo Log、Bin Log)
InnoDB是一个带有ACID事务支持的存储引擎,其中redo log和undo log是其实现原子性、一致性、隔离性和持久性(ACID)的重要机制。 Redo Log(重做日志) Redo log主要用于实现事务的持久性。它记录了后续可以用来恢复数据…...

HarmonyOS如何创建及调用三方库
介绍 本篇主要向开发者展示了在Stage模型中,如何调用已经上架到三方库中心的社区库和项目内创建的本地库。效果图如下: 相关概念 Navigation:一般作为Page页面的根容器,通过属性设置来展示页面的标题、工具栏、菜单。Tabs&#…...

我手写的轮子开源了
我手写的轮子开源了 文章目录 1.gitee坐标和地址1.1.gitee坐标1.2.gitee地址 2.github坐标和地址2.1.github坐标2.2.github地址 3.总结 1.gitee坐标和地址 1.1.gitee坐标 <dependency><groupId>io.gitee.bigbigfeifei</groupId><artifactId>es-sprin…...
第十九章 linux部署scrapyd
文章目录 1. linux部署python环境1. 部署python源文件环境2. 下载python3. 解压安装包4. 安装5. 配置环境变量6. 检查是否安装成功7. 准备python使用的包8. 安装scrapyd9. 配置scrapyd10. 开放6800端口 2. 部署gerapy1. 本机下载包2. 初始化3. 进入gerapy同步数据库4. 创建用户…...

微信打卡小程序怎么做_用户的每日习惯培养神器
微信打卡小程序:你的每日习惯培养神器 在这个快节奏的现代社会,我们每天都在忙碌中度过,有时候甚至会忘记自己曾经立下的那些小目标、小习惯。然而,随着科技的不断发展,微信打卡小程序的出现,为我们的生活…...
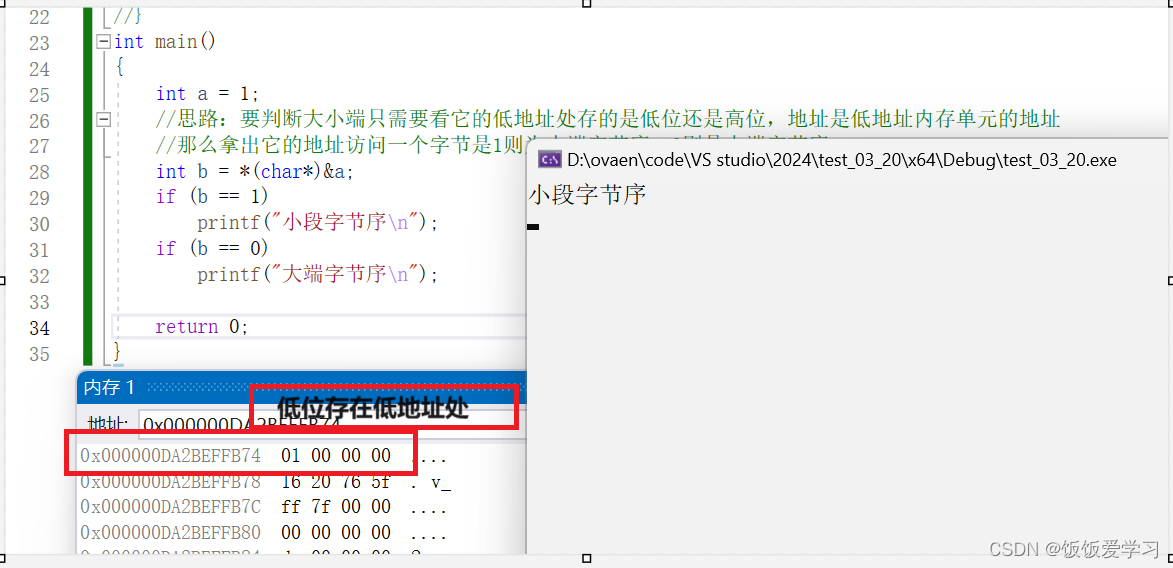
C语言数据在内存中的存储
reference n.提及,谈到;参考,查阅;(引自书或诗歌的)引言,引文; 引文的作者,参考书目;(帮助或意见的)征求,征询;…...

管理公司员工上网行为的软件都有哪些?
随着互联网的飞速发展,企业面临的网络安全威胁也日益加剧。为了保护企业数据安全、提高工作效率,上网行为管理系统及其相关管理软件应运而生。 未来,随着技术的不断进步和网络安全威胁的不断演变,上网行为管理系统及其管理软件将不…...

手撕C语言题典——逆序输出
有这样一个问题:读入一些整数,逆序输出到一行中。已知的是该整数不超过100个。我们该怎么办呢?我们先将这些整数循环输入,输入每个整数之后,我们只能将数组存下来,而这个地方就是数组。 本章可能用到的知识…...

如果保障服务器的安全
如果保障服务器的安全 一、修改它最开始的密码,后期也要一直更换。一般如果有客户来了服务器的话,服务器厂商都会提前把所有的系统都装好,之后再把这个权限交到用户的手里。很多用户可能在这方面不会特别注意,密码也不修改&#x…...

【SQL】1280. 学生们参加各科测试的次数 (笛卡尔积)
前述 知识点回顾:数据库中的四大join & 笛卡尔乘积(以MySQL为例) 笛卡尔积的两种写法 select * from stu,class; select * from stu cross join class; 题目描述 leetcode题目:1280. 学生们参加各科测试的次数 Code 写法…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
