有ai写文案的工具吗?分享5款好用的工具!
在数字化时代,人工智能(AI)已渗透到我们生活的方方面面,包括内容创作领域。AI写文案的软件以其高效、便捷的特点,正逐渐受到广大内容创作者、营销人员、甚至普通用户的青睐。本文将为您盘点几款热门的AI写文案软件,助您在内容创作的道路上走得更远。

- 聪明灵犀
聪明灵犀的AI文案写作功能,凭借其强大的自然语言处理和深度学习技术,能够自动生成高质量、有吸引力的文案。无论是新闻报道、广告推广还是社交媒体内容,它都能迅速生成符合要求的文本,为自媒体创作者提供强大的支持。
二、Copy.ai
Copy.ai是一款专门为内容创作者设计的AI写作工具。它提供了多种模板,涵盖广告、社交媒体、博客、电子邮件等,用户只需填写几个关键信息,即可生成个性化的文案。同时,Copy.ai还具备语法检查、SEO优化等功能,让文案更加专业、易读。

三、Jasper AI
Jasper AI是另一款功能强大的AI写作软件。它支持多种写作风格,如正式、幽默、创意等,能够满足不同场合的需求。Jasper AI还提供了内容大纲、关键词优化等实用功能,帮助用户快速生成高质量的文案。

四、Rytr
Rytr是一款简单易用的AI写作软件。它支持多种语言和内容类型,如博客文章、广告、社交媒体帖子等。Rytr还提供了实时预览和编辑功能,用户可以随时调整文案内容和风格。

五、Article Forge
Article Forge是一款专注于生成高质量文章的AI写作工具。它可以根据用户提供的关键词和主题,自动生成结构完整、内容丰富的文章。Article Forge还支持批量生成和发布文章,适合需要大量内容支持的用户。

AI写文案的软件正以其高效、便捷的特点改变着我们的内容创作方式。从GPT系列到各类专用AI写作工具,这些软件为我们提供了更多元化、更高质量的文案创作选择。然而,我们也要认识到AI工具的局限性,它们在情感表达、创新思维等方面仍有待提升。因此,在使用AI写文案软件时,我们要充分发挥其优势,结合人类的创意和智慧,共同推动内容创作领域的发展。
相关文章:

有ai写文案的工具吗?分享5款好用的工具!
在数字化时代,人工智能(AI)已渗透到我们生活的方方面面,包括内容创作领域。AI写文案的软件以其高效、便捷的特点,正逐渐受到广大内容创作者、营销人员、甚至普通用户的青睐。本文将为您盘点几款热门的AI写文案软件&…...

docker+k8s相关面试题
dockerk8s k8s详细介绍docker的工作原理docker的组成docker与传统虚拟机的区别docker技术的三大核心概念centos镜像几个G,但是docker centos镜像才几百兆镜像的分层结构以及为什么要使用镜像的分层结构容器的copy-on-write特性,修改容器里面的内容会修改…...
力扣爆刷第101天之hot100五连刷91-95
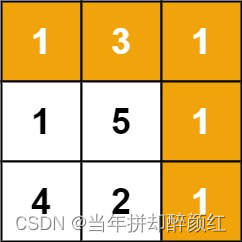
力扣爆刷第101天之hot100五连刷91-95 文章目录 力扣爆刷第101天之hot100五连刷91-95一、62. 不同路径二、64. 最小路径和三、5. 最长回文子串四、1143. 最长公共子序列五、72. 编辑距离 一、62. 不同路径 题目链接:https://leetcode.cn/problems/unique-paths/desc…...
前端vue实现甘特图
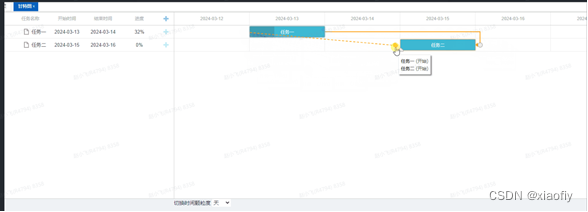
1 什么是甘特图 甘特图(Gantt chart)又称为横道图、条状图(Bar chart)。以提出者亨利L甘特先生的名字命名,是项目管理、生产排程、节点管理中非常常见的一个功能。 甘特图内在思想简单,即以图示的方式通过活动列表和时间刻度形象地表示出任何特定项目的…...

SQLiteC/C++接口详细介绍之sqlite3类(十五)
返回目录:SQLite—免费开源数据库系列文章目录 上一篇:SQLiteC/C接口详细介绍之sqlite3类(十四) 下一篇:SQLiteC/C接口详细介绍之sqlite3类(十六) 47.sqlite3_set_authorizer 用法ÿ…...
)
每日三个JAVA经典面试题(十八)
1.volatile 关键字的作用 在Java中,volatile关键字用于声明变量,以确保该变量的更新对所有线程都是可见的,即当一个线程修改了一个volatile变量的值,这个新值对于其他线程来说是立即得知的。volatile关键字有两个主要作用&#x…...
RPC 和 序列化
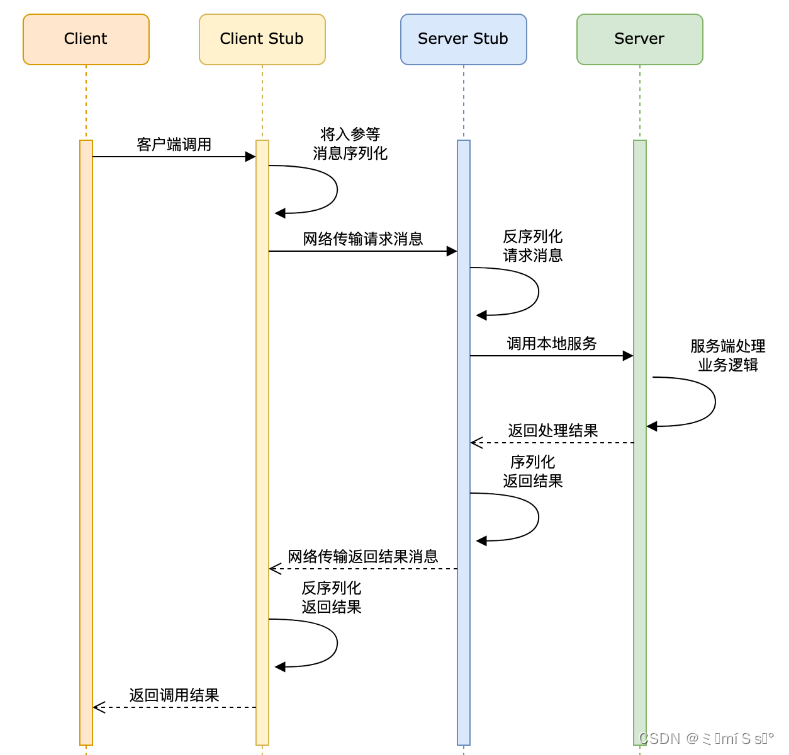
RPC 1 RPC调用流程 1.1 clerk客户端调用远程服务 Clerk::PutAppend() raftServerRpcUtil::PutAppend() raftServerRpcUtil是client与kvserver通信的入口, 包含kvserver功能的一对一映射:Get/PutAppend,通过stub对象——raftKVRpcProctoc:…...
【原创】三十分钟实时数据可视化网站前后端教程 Scrapy + Django + React 保姆级教程向
这个本来是想做视频的,所以是以讲稿的形式写的。最后没做视频,但是觉得这篇文还是值得记录一下。真的要多记录,不然一些不常用的东西即使做过几个月又有点陌生了。 文章目录 爬虫 SCRAPYxpath 后端 DJANGO前端 REACT Hello大家好这里是小鱼&a…...

MySQL的备份
为什么要备份: 1.保证重要的数据不丢失 2.数据转移 MySQL数据库备份的方式: 1.直接拷贝物理文件 2.在可视化工具中手动导出 (1)在想要导出的表或者数据库中,右键,选择备份或导出 使用命令行导出 MyS…...
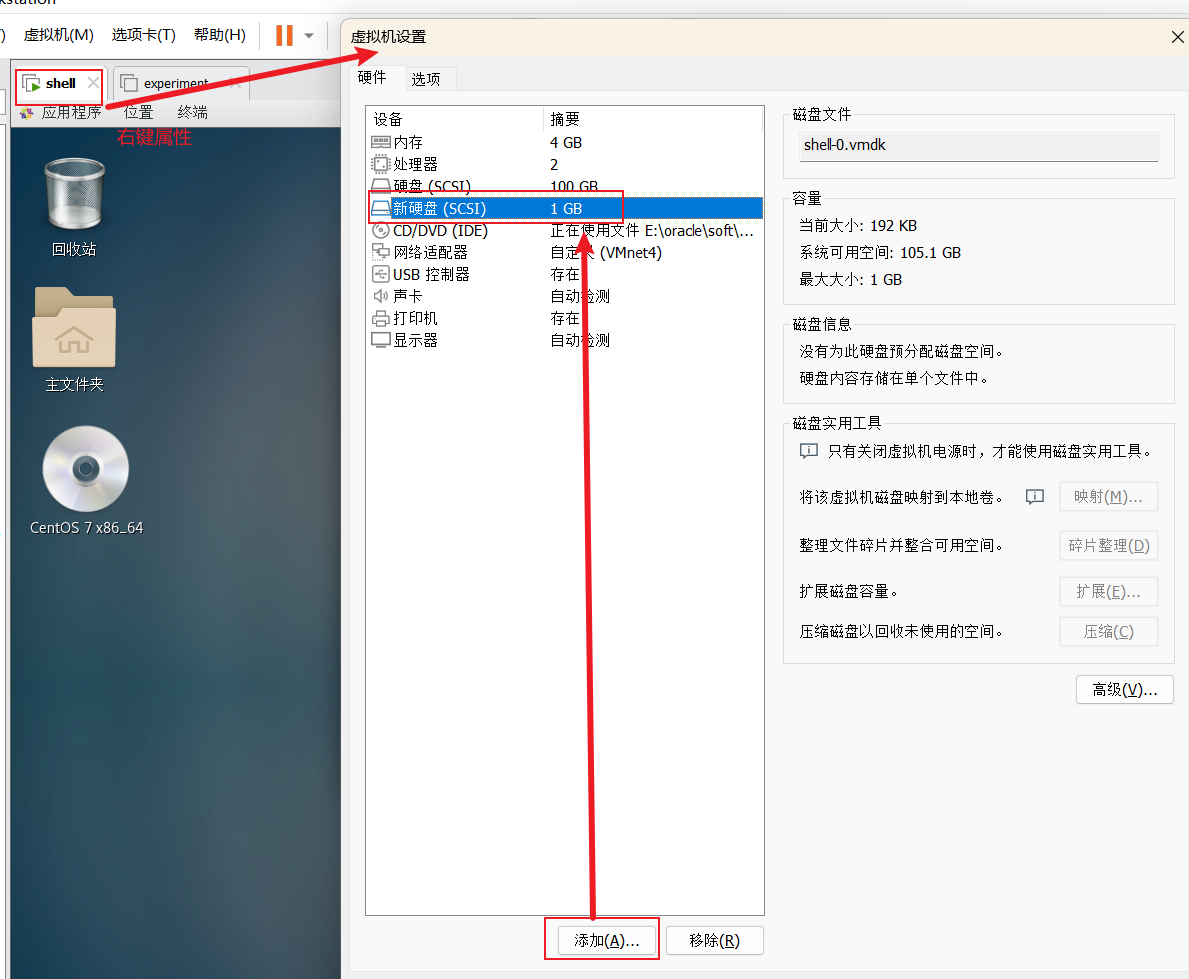
Linux 磁盘的一生
注意:实验环境都是使用VMware模拟 磁盘接口类型这里vm中是SCSI,扩展sata,ide(有时间可以看看或者磁盘的历史) 总结:磁盘从有到无—类似于建房子到可以住 ————————————————————————————————————…...

C#配置连接数据库字段
在Web.config文件中 添加如下配置 <!--连接数据库字段--><connectionStrings><add name"sql" connectionString"server.;uidsa;pwd8888;databaseArticleWebSite" /></connectionStrings>...

QCOM和其他常见芯片平台术语缩写
1 QCOM 1.1 General Qualcomm: Quality Communications ALSA DCP:ALSA由DAI、Codec、Platform三部分组成 ALSA TLV:Type-Length-Value Alternative Mode: 替代模式 ANC:Automatic Noise Canceller ASM: Anntena Switch Module AT:…...

css页面布局
CSS属性书写顺序(重点) 建议遵循以下顺序: 布局定位属性:display / position/ float / clear / visibility / overflow(建议display第一个写,毕竟关系到模式) 自身属性:width / height / margin / padding / border / background…...
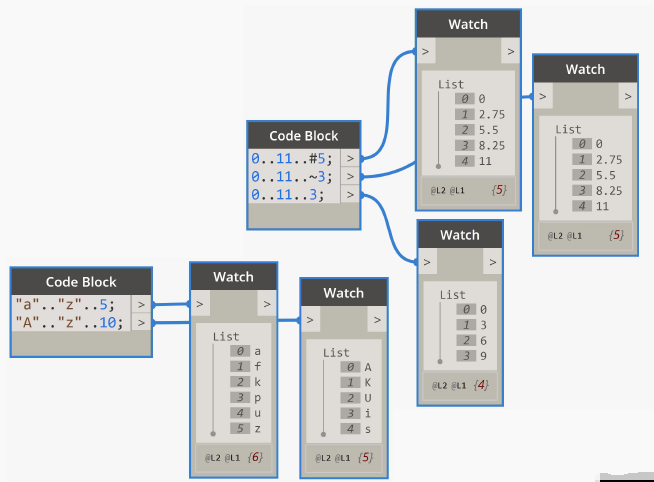
6、Design Script之列表
Range 在DesignScript中,Range是从起点到终点的一系列数字,使用指定的步距(间距类型),并有以下的初始化方法: start..end..step; start..end..#amount; start..end..~approximate; Range可以是数字的,也可以是字母的。 字母范围因大小写而异。 开始,结束. .#数量范围(…...

Mysql数据库的多实例部署
mysql多实例部署 先进行软件下载 上传二进制格式的mysql软件包 [rootcjy ~]# ls anaconda-ks.cfg mysql-8.0.35-linux-glibc2.28-x86_64.tar.xz配置用户和组并解压二进制程序至/usr/local下 创建用户和组 [rootcjy ~]# useradd -r -s /sbin/nologin -M mysql解压软件至/usr…...
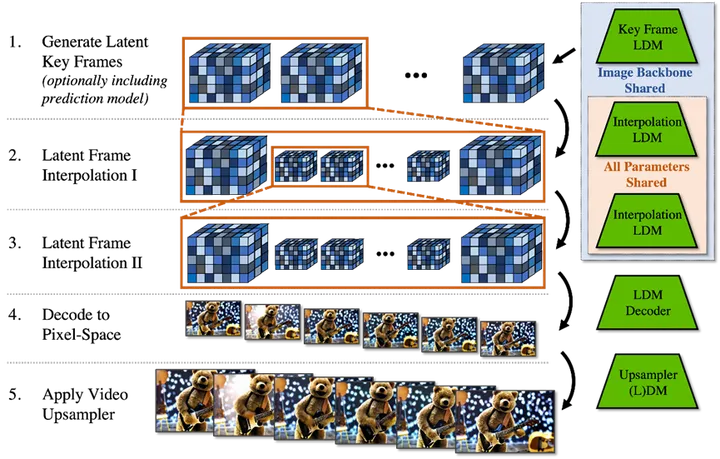
陈巍:Sora大模型技术精要万字详解(上)——原理、关键技术、模型架构详解与应用
目录 收起 1 Sora的技术特点与原理 1.1 技术特点概述 1.2 时间长度与时序一致性 1.3 真实世界物理状态模拟 1.4 Sora原理 1.4.1扩散模型与单帧图像的生成 1.4.2 Transformer模型与连续视频语义的生成 1.4.3 从文本输入到视频生成 2 Sora的关键技术 2.1 传统文生图技…...
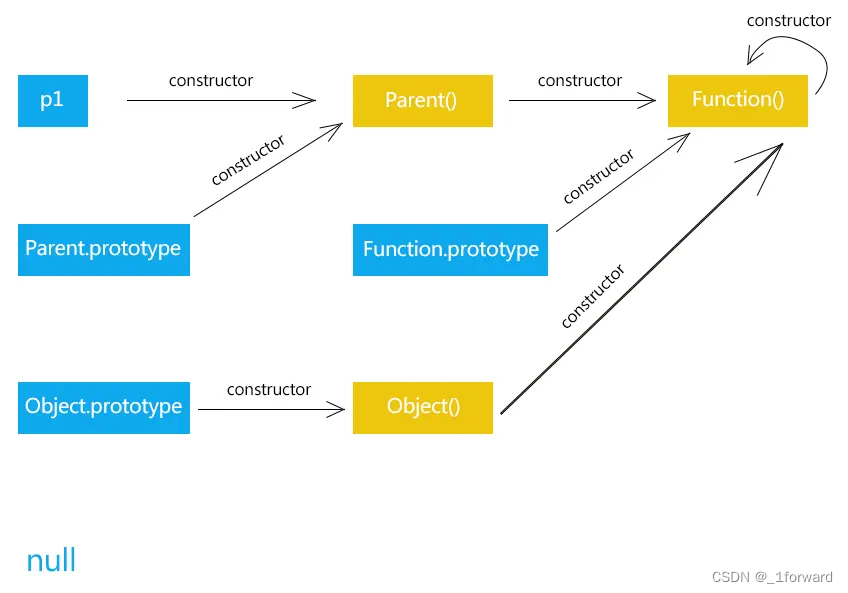
JS原型和原型链的理解
原型链图,图中Parent是构造函数,p1是通过Parent实例化出来的一个对象 前置知识 js中对象和函数的关系,函数其实是对象的一种 函数、构造函数的区别,任何函数都可以作为构造函数,但是并不能将任意函数叫做构造函数&…...

力扣题单(小白友好)
力扣题单 算法小白自用题单,目前对于一些简单的数据结构感觉掌握的还可以,但是力扣很多题还是需要看题解,不够熟练;故整理了一份题单,用于巩固练习; 网上确实有很多对于算法分类讲解的网站,but:有一丢丢选择困难症,每天不知道该刷什么题,再加上网站对于一类题一般就有十几道题目…...

王道c语言ch11-单链表的新建、插入、删除例题
王道c语言ch11-单链表的新建、插入、删除例题 #include <stdio.h> #include <stdlib.h> #define END 33typedef int ElemType;typedef struct LNote {ElemType data;struct LNote *next; } LNote, *LinkList;//头插法 void list_head_insert(LinkList &L) {El…...

蓝桥杯刷题--python-23
2.危险系数 - 蓝桥云课 (lanqiao.cn) n, m map(int, input().split()) map_ [[] for i in range(n 1)] used [0 for i in range(n 1)] used_ [0 for i in range(n 1)] cnt 0 res [] for _ in range(m):u, v map(int, input().split())map_[u].append(v)map_[v].appen…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
