高级数据结构 <AVL树>
本文已收录至《数据结构(C/C++语言)》专栏!
作者:ARMCSKGT

目录
- 前言
- 正文
- AVL树的性质
- AVL树的定义
- AVL树的插入函数
- 左单旋
- 右单旋
- 右左双旋
- 左右双旋
- 检验AVL树的合法性
- 关于AVL树
- 最后
前言
前面我们学习了二叉树,普通的二叉树没有任何特殊性质,所以后面我们又学习了二叉搜索树,这种有序的结构一定程度上优化了二叉树的性能,但是普通的二叉搜索树在特殊情况下,例如插入序列从大到小有序时,二叉搜索树会退化成类似于链表的单支数,此时性能变为O(n),为了解决这个问题,科学家在二叉搜索树的基础上再次进行升级,而有了我们现在常见的 AVL树 和 红黑树 ,本节我们将介绍AVL树的基础性质。

正文
在介绍AVL树之前,如果你没有了解过 二叉搜索树 或 二叉树,请移步先了解前置知识!
本节介绍AVL树默认中序遍历为升序序列
AVL树的性质
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家 G.M.Adelson-Velskii 和 E.M.Landis 在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
简而言之,AVL树通过一个 平衡因子bf(右子树深度减去左子树深度) 来记录根节点左右子树深度的差,一般情况下,平衡因子只会有五种情况:
- 左子树比右子树深度高两层,此时平衡因子为 -2 ,此时需要对树进行旋转调整
- 左子树比右子树深度高一层,此时平衡因子为 -1
- 左子树与右子树深度相等,此时平衡因子为 0
- 左子树比右子树深度低一层,此时平衡因子为 1
- 左子树比右子树深度低两层,此时平衡因子为 2 ,此时需要对树进行旋转调整
综上,如果二叉搜索树具备以下性质,则为AVL树:
- 左右子树的高度之差(平衡因子)的绝对值不超过 1
- 它的左右子树都是 AVL 树
AVL树结构(节点上的数字就是平衡因子):
这颗树没有出现不平衡的情况,每个节点的平衡因子的绝对值不超过2。
这样看来,AVL树是一颗高度平衡的二叉搜索树,如果AVL树有N个节点,则AVL树的高度为 log n \log_n logn,此时找到任意节点的时间复杂度都是O( log 2 N \log_2N log2N)。
我们学习AVL树主要是研究其插入节点后如何保持平衡的思想!
AVL树的定义
AVL树在二叉树的基础上,增加了一个指针指向了父节点以及一个平衡因子,所以AVL树是三叉链结构!
节点定义代码:#include <iostream>template<class K,class V> struct TreeNode {TreeNode<K, V>* _left; // 左子树TreeNode<K, V>* _right; // 右子树TreeNode<K, V>* _parent; // 父节点std::pair<K, V> _val; // 节点键值对(节点值)int _bf; // 平衡因子TreeNode():_left (nullptr),_right (nullptr),_parent(nullptr),_val(pair<K,V>()),_bf(0){}TreeNode(const pair<K,V>& val):_left (nullptr), _right (nullptr), _parent(nullptr), _val(val), _bf(0){}TreeNode(const K& key,const V& val):_left(nullptr), _right(nullptr), _parent(nullptr), _val({key,val}), _bf(0){} };
AVL树的定义比较简单,只需要一个根节点_root记录即可。
但是为了我们可以控制对比的函数,以便随我们指定的方式去插入,就像sort函数一样,可以通过仿函数控制升序和降序排序,所以我们还需要一个模板参数去作为比较函数!
AVL树定义://仿函数控制比较方式 template<class T> //升序 struct less { bool operator()(const T& left, const T& right) { return left < right; } }; template<class T> //降序 struct greater { bool operator()(const T& left, const T& right) { return left > right; } };//AVL树定义 默认升序(按中序输出序列) template<class K, class V, class Compare = less<K>> class AVLTree {typedef std::pair<K, V> val_type; //值类型typedef TreeNode<K, V> Node; //节点类型 public:AVLTree() :_root(nullptr), _size(0) {}private:Node* _root; //根节点size_t _size; //节点数量Compare _com; //比较函数 };
AVL树的插入函数
在二叉搜索树的插入函数基础上,AVL树的插入操作还需要对父节点的平衡因子进行调节,并在失衡的根节点处进行旋转调整。
AVL树插入流程:
- 如果是第一次插入节点,直接赋值给 _root 作为根节点,_size+1。
- 将插入值的key与当前节点值传入 _com函数 中对比,当函数返回true时向左子树走,返回false时向右子树走,如果走到空则跳出准备插入,如果相等则返回当前节点值。
- 根据节点值与插入值key在_com函数中的对比结果,决定插入到父节点的左子树还是右子树。
- 调整父节点的平衡因子,如果出现失衡(平衡因子绝对值为2)则进行旋转,并依次向上继续调整祖父节点,直到当前父节点平衡因子为0或节点为树的根节点为止。
- _size+1并返回插入结果。
关于AVL树的返回值:AVL树返回值为 pair<val_type,bool>,当插入成功在返回节点值的同时并返回true,当插入失败(遇到相等值节点时)返回false。
插入函数代码:
//插入函数 pair<val_type, bool> insert(const val_type& data) {//首次插入特殊处理if (nullptr == _root){Node* newnode = new Node(data);_root = newnode;++_size;return { data,true };}//寻找合适的插入位置Node* newnode = new Node(data);Node* parent = _root;Node* cur = _root;while (cur){if (_com(data.first, cur->_val.first)) // <{parent = cur;cur = cur->_left;}else if (_com(cur->_val.first, data.first)) // >{parent = cur;cur = cur->_right;}//找到相同值节点 返回false和节点值else return { data,false}; // ==}//将新节点插入所寻找的父节点下if (_com(data.first, parent->_val.first)) parent->_left = newnode;else parent->_right = newnode;newnode->_parent = parent;cur = newnode;while (parent){//调整父节点平衡因子if (parent->_left == cur) --(parent->_bf);else if (parent->_right == cur) ++(parent->_bf);//调整和旋转if (parent->_bf == 1 || parent->_bf == -1){parent = parent->_parent;cur = cur->_parent;}else if (parent->_bf == 0) break;else //开始调整和旋转{if (parent->_bf == -2 && cur->_bf == -1) RotateR(parent); //右单旋else if (parent->_bf == 2 && cur->_bf == 1) RotateL(parent); //左单旋else if (parent->_bf == -2 && cur->_bf == 1) RotateLR(parent); //左右旋else if (parent->_bf == 2 && cur->_bf == -1) RotateRL(parent); //右左旋else { assert(false); }}}++_size;return { data,true }; }
关于节点调整流程:
关于旋转调整节点,我们接下来进行详细探究!关于需要调整的情况,一共可以分为四大类:
是否旋转,取决于parent和cur节点的平衡因子:
parent(父节点)平衡因子 cur(子节点)平衡因子 操作 -2 -1 右单旋 2 1 左单旋 -2 1 左右双旋 2 -1 右左双旋
左单旋
当根节点的右子树平衡因子为1的情况下,仍然向右子树中插入比右子树节点值大的节点,此时就会导致根节点平衡因子为2,右子树平衡因子为1,此时就需要左单旋。
当我们向20节点的右子树中插入35时,35是该树中的最大节点,便会插入在最右节点,此时30节点的平衡因子变为1,25节点则变为2,需要对其进行左单旋。
左单旋的函数代码:
//左单旋 void RotateL(Node* parent) {//parent右子节点Node* childR = parent->_right;//parent右子节点的左子节点Node* childRL = childR->_left;//parent右子节点的右子节点Node* childRR = childR->_right;//parent节点的父节点Node* pparent = parent->_parent;//parent节点的右指向childR的左子树parent->_right = childRL;//如果childRL节点存在 则链接与parent节点的关系 否则parent->_right指向空if (childRL) childRL->_parent = parent;//将childR的左指向parent 构建链接关系childR->_left = parent;parent->_parent = childR;//与pparent构建链接关系 如果pparent为_root根节点 则设置_rootif (pparent == nullptr){_root = childR;_root->_parent = nullptr;}else //否则查看原parent节点是pparent的左还是右子树 插入原parent位置{if (pparent->_left = parent) pparent->_left = childR;else pparent->_right = childR;childR->_parent = pparent;}//更新受影响节点的平衡因子parent->_bf = childR->_bf = 0; }旋转过程简而言之就是更改节点的链接关系,使其深度降低!
对于上面图中的树,我们根据左单旋进行调整:
左单旋过程梳理:
- parent节点与childRL节点构建链接关系
- childR节点的左子树置为parent,并相互构建链接关系
- 判断pparent是否为空,不为空则将childR与pparent构建链接关系
- 将parent节点与childR节点的平衡因子置为0
注意:这里在构建链接关系时,一定要注意构建与父节点的关系,容易忘记;childRL节点可能为空,如果为空则不需要与其新父节点(parent)构建链接关系,需要if判断!
右单旋
当根节点的左子树平衡因子为-1的情况下,仍然向左子树中插入比左子树节点值小的节点,此时就会导致根节点平衡因子为-2,左子树平衡因子为-1,此时就需要右单旋。
右单旋与左单旋相似,只不过指针的调整方式不同。
当节点3插入后,节点10的平衡因子(左右子树高度差为2)为-2,此时插入的节点位于左子树的左侧,此时需要右旋转。
右单旋的函数代码:
//右单旋 void RotateR(Node* parent) {Node* childL = parent->_left;Node* childLL = childL->_left;Node* childLR = childL->_right;Node* pparent = parent->_parent;parent->_left = childLR;if (childLR) childLR->_parent = parent;childL->_right = parent;parent->_parent = childL;if (pparent == nullptr){_root = childL;_root->_parent = nullptr;}else{if (pparent->_left == parent) pparent->_left = childL;else pparent->_right = childL;childL->_parent = pparent;}parent->_bf = childL->_bf = 0; }
对于上面图中的树,我们根据右单旋进行调整:
右单旋过程梳理:
- parent节点与childLR节点构建链接关系
- childL节点的右子树置为parent,并相互构建链接关系
- 判断pparent是否为空,不为空则将childL与pparent构建链接关系
- 将parent节点与childL节点的平衡因子置为0
注意:这里在构建链接关系时,一定要注意构建与父节点的关系,容易忘记;childLR节点可能为空,如果为空则不需要与其新父节点(parent)构建链接关系,需要if判断!
右左双旋
当我们将值插入(高度差为1的树时)右子树右侧时会引发左单旋,当插入左子树左侧时会引发右单旋。
相反,如果将值插入右子树左侧或左子树右侧,则会引发双旋。
如果插入的是右子树左侧,此时parent平衡因子为,那么单旋就不能解决问题了,此时需要右左双旋,详细解释就是先 进行右单旋 再进行左单旋,这样才能降低高度。
关于以下情况,就是需要进行右左双旋:
右左双旋代码:
//右左双旋 void RotateRL(Node* parent) {Node* childR = parent->_right;Node* childRL = childR->_left;int bf = childRL->_bf;RotateR(childR);RotateL(parent);/*AB CDE*/if (bf == -1){parent->_bf = 0;childR->_bf = 1;childRL->_bf = 0;}/*AB CDE*/else if (bf == 1){parent->_bf = -1;childR->_bf = 0;childRL->_bf = 0;}/*ABC*/else if (bf == 0){parent->_bf = 0;childR->_bf = 0;childRL->_bf = 0;}//如果出现其他情况,则表示代码有问题,需要检查else assert(false); }关于右左双旋,可以结合下图理解(三列情况,对应三种不同的平衡因子调整):
关于右左双旋的过程:
- 先确定parent和childR和childRL节点
- 对childR进行右单旋(将childRL变成childR的父节点)
- 对parent进行左单旋(再将childRL变成childR的父节点)
- 调整parent,childR和childRL节点的平衡因子(根据childRL节点平衡因子调整)
关于节点平衡因子的调整,从上图看出来,需要根据childRL节点来进行判断:
- 当childRL平衡因子为 0 :
parent的平衡因子调整为0,childR的平衡因子调整为0,childRL平衡因子调整为0。- 当childRL平衡因子为 -1 :
parent的平衡因子调整为0,childR的平衡因子调整为1,childRL平衡因子调整为0。- 当childRL平衡因子为 1 :
parent的平衡因子调整为-1,childR的平衡因子调整为0,childRL平衡因子调整为0。
注意:右左双旋中,对childR进行右单旋转再对parent进行左单旋,这个顺序不能颠倒,且平衡因子的调整必须根据childRL平衡因子进行调整。
左右双旋
当节点插入到左子树的右侧时,此时parent平衡因子为-2且childR平衡因子为1,此时需要左右双旋,即需要 先进行左单旋,再进行右单旋 才能降低高度。
关于以下插入情况,此时的树需要进行左右双旋:
左右双旋代码:
//左右双旋 void RotateLR(Node* parent) {Node* childL = parent->_left;Node* childLR = childL->_right;int bf = childLR->_bf;RotateL(childL);RotateR(parent);/*AB CD EF*/if (bf == -1){childL->_bf = 0;childLR->_bf = 0;parent->_bf = 1;}/*AB CD EF*/else if (bf == 1){childL->_bf = -1;childLR->_bf = 0;parent->_bf = 0;}/** A* B* C*/else if (bf == 0){childL->_bf = 0;childLR->_bf = 0;parent->_bf = 0;}//如果出现其他情况,则表示代码有问题,需要检查else assert(false); }
关于右左双旋,可以结合下图理解(三列情况,对应三种不同的平衡因子调整):
关于左右双旋的过程:
- 先确定parent和childL和childLR节点
- 对childL进行左单旋(将childLR变成childL的父节点)
- 对parent进行右单旋(再将childLR变成parent的父节点)
- 调整parent,childL和childLR节点的平衡因子(根据childLR节点平衡因子调整)
关于节点平衡因子的调整,从上图看出来,需要根据childRL节点来进行判断:
- 当childLR平衡因子为 0 :
parent的平衡因子调整为0,childL的平衡因子调整为0,childLR平衡因子调整为0。- 当childLR平衡因子为 -1 :
parent的平衡因子调整为1,childL的平衡因子调整为0,childLR平衡因子调整为0。- 当childLR平衡因子为 1 :
parent的平衡因子调整为0,childL的平衡因子调整为-1,childLR平衡因子调整为0。
注意:左右双旋中,对childL进行右单旋转再对parent进行左单旋,这个顺序不能颠倒,且平衡因子的调整必须根据childLR平衡因子进行调整。
AVL树主要值得学习的地方就在插入,学习其控制树的高度差的思想和旋转思想。
检验AVL树的合法性
检验AVL树是否合格(是否没有bug),还需要从其定义入手。
空树是满足AVL树性质,且满足以下条件,则是AVL树:
- 右子树减去左子树深度的绝对值不超过1
- 右子树减去左子树深度等于根节点平衡因子
- 每棵子树都满足该条件
以上条件满足任意一个,就是AVL树。
我们代码实现采用递归方式,在类中需要写一个递归函数再进行封装!
代码实现:
//检查AVL树合法性-调用函数 bool isAVL() { return _isAVL(_root); }//获取AVL树高度-调用函数 int getHigh() { return _getHigh(_root); }//检查AVL树合法性-执行函数 bool _isAVL(Node* root) {if (root == nullptr) return true;//获取左右子树高度int left = _getHigh(root->_left);int right = _getHigh(root->_right);//如果右子树减左子树高度差的绝对值小于1 且差值与根的平衡因子相等 就继续检查子树if (abs(right - left) <= 1 && (right - left) == root->_bf) return true && _isAVL(root->_left) && >_isAVL(root->_right);return false; }//获取树的深度-执行函数 int _getHigh(Node* root) {if (root == nullptr) return 0;int left = _getHigh(root->_left);int right = _getHigh(root->_right);return left > right ? left + 1 : right + 1; }
测试代码:
int main() {const int N = 10000;AVLTree::AVLTree<int,int> t;for (int i = 0; i <= N; ++i) t.insert({i,i});if (t.isAVL()) cout << "合法" << endl;else cout << "不合法" << endl;cout << "树高度:" << t.getHigh() << endl;return 0; }
我们插入10001个节点,此时树合法且高度为14!
2 13 = 8192 , 2 14 = 16384 2^{13}=8192 ,2^{14}=16384 213=8192,214=16384
通过对高度的平方运算,结果符合要求!
关于AVL树
AVL树是一棵对身材要求及其严格的树,时时刻刻要求自己左右接近对称(左右高度差不超过1)。
AVL树的优缺点:
- 优点: 因为其严格的要求,当树中稍微出现退化趋势就会立刻被调整,所以对于AVL树的查询时间非常快,约为 l o g 2 N log_2N log2N。
- 缺点: 因为其严格的条件,导致AVL树在碰到有序序列时可能会频繁旋转调整,在删除情况下更是有可能一直调整到根节点,因为频繁旋转非常浪费性能,所以导致插入效率下降。
AVL树的使用场景:
AVL树严格的平衡条件,导致其查询效率极高,在不频繁增删的情况下,也就是静态树(只查只读) 的情况下,使用AVL树会的查询效率是极好的,但是在很多场景中,增删查改是并存的,此时我们不得不考虑摒弃一些查询时间去弥补插入删除的效率,也就是需要一棵与AVL树差不多,但是没有AVL树要求这么严格的二叉搜索树,这棵树就是红黑树,红黑树可以做的比AVL树调整次数少的情况下,性能差距不超过2倍,下一节我们将介绍红黑树!
最后
AVL树的介绍到这里就差不多了,我们首先说明了二叉搜索树的缺点,引入AVL树对其进行强化,AVL树的复杂之处在于其旋转调整,所以我们通过AVL树的插入介绍旋转调整,至于删除操作相对于插入函数更加复杂,有兴趣的小伙伴可以了解,对于AVL树的基本性质就是这些了!
本次 <AVL树> 就先介绍到这里啦,希望能够尽可能帮助到大家。
如果文章中有瑕疵,还请各位大佬细心点评和留言,我将立即修补错误,谢谢!
本节涉及代码:AVL树博客代码

🌟其他文章阅读推荐🌟
数据结构初级<二叉搜索树>
数据结构初级<二叉树>
C++ <继承>
C++ <多态>
C++ <STL容器适配器>
🌹欢迎读者多多浏览多多支持!🌹
相关文章:

高级数据结构 <AVL树>
本文已收录至《数据结构(C/C语言)》专栏! 作者:ARMCSKGT 目录 前言正文AVL树的性质AVL树的定义AVL树的插入函数左单旋右单旋右左双旋左右双旋 检验AVL树的合法性关于AVL树 最后 前言 前面我们学习了二叉树,普通的二叉树没有任何特殊性质&…...

在springboot中利用Redis实现延迟队列
文章目录 前言一、基本思路二、springboot实现案例三、测试总结 前言 在开发过程中,有很多场景都需要用到延迟队列来解决。目前支持延迟队列的中间件也不少,特别是基于JMS模式下的消息中间件基本上都支持延迟队列。但是有时我们项目规模可能比较小&…...

UpGrow评论:AI能将我的Instagram粉丝数增加10倍吗?
UpGrow Review: Can AI Grow My Instagram Followers 10X? 概述 UpGrow是一款专注于Instagram增长的AI驱动型社交媒体工具。它通过其庞大的300多人的网络,先进的定位功能,实时分析以及卓越的客户服务,帮助用户有机地增长Instagram关注者。…...

申请软著提交的演示视频有什么要求
申请软件著作权时,演示视频是一个重要的材料,主要用于展示软件的功能和操作流程。演示视频的要求可能会根据不同的申请机构和项目有所不同,但一般来说,以下是几个常见的要求: 内容完整性:演示视频需要展示…...
mac【启动elasticsearch报错:can not run elasticsearch as root
mac【启动elasticsearch报错:can not run elasticsearch as root 问题原因 es默认不能用root用户启动,生产环境建议为elasticsearch创建用户。 解决方案 为elaticsearch创建用户并赋予相应权限。 尝试了以下命令创建用户,adduser esh 和u…...
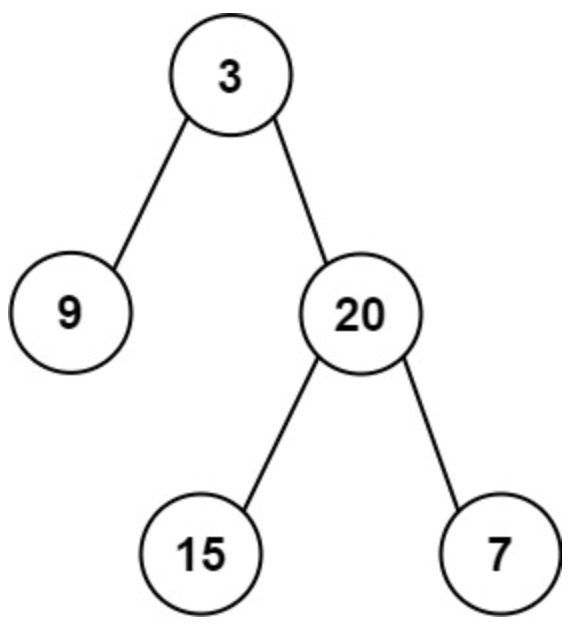
面试算法-65-二叉树的层平均值
题目 给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:[3.00000,14.50000,11.00000] 解释:第 0 层的…...

Linux: boot: latency启动延迟分析
https://elinux.org/images/6/64/Chris-simmonds-boot-time-elce-2017_0.pdf https://www.hcltech.com/sites/default/files/documents/resources/whitepaper/files/an_insight_to_optimize_embedded_linux_boot_time_performance.pdf 无意看到这个启动延迟分析,虽…...

QT界面制作
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);this->setWindowFlag(Qt::FramelessWindowHint);//接收动图QMovie *mv new QMovie(":/pictrue/th.gif…...
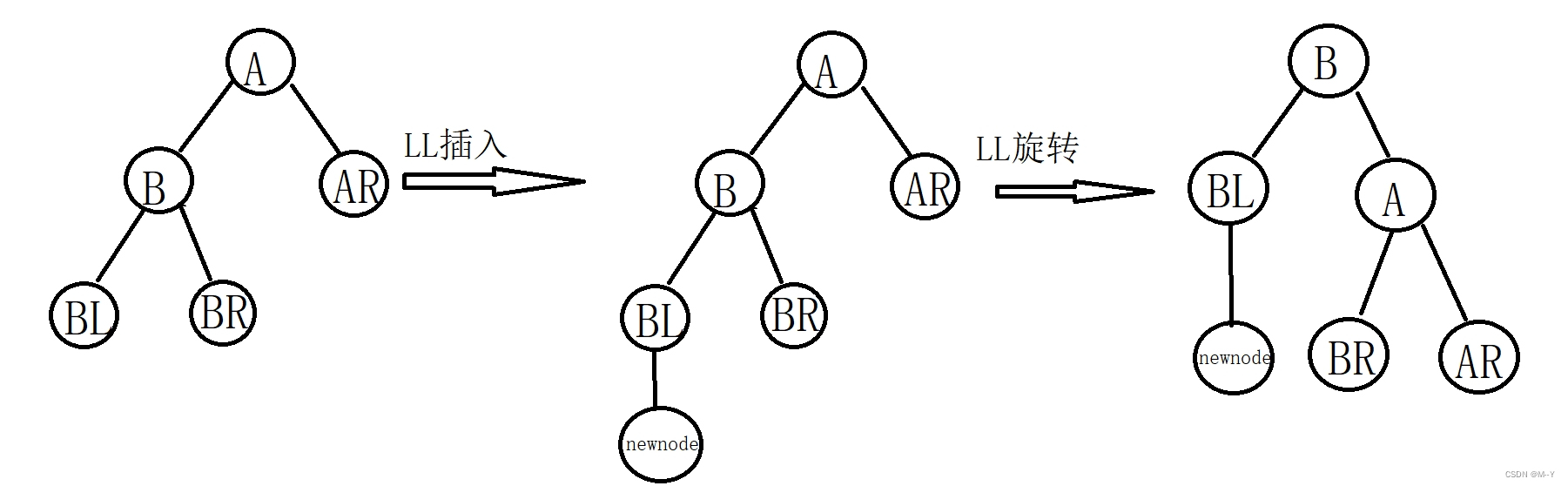
进阶二叉树
目录 二叉树 二叉搜索树 二叉搜索树的定义 二叉搜索树的操作 哈夫曼树 哈夫曼树的定义 哈夫曼树的构造 哈夫曼树的性质 平衡二叉树 平衡二叉树的定义: 平衡二叉树的插入调整 1.LL插入/LL旋转 2.RR插入/RR旋转 3.LR插入/LR旋转 4.RL插入/RL旋转 二叉树…...

无人机拦截
配置yolo CUDA报错 nvcc fatal : Unsupported gpu architecture compute_30.(1)查看显卡匹配型号:https://blog.csdn.net/u013308762/article/details/121658823 (2)查看显卡:nvidia-smi -a 》NVIDIA GeF…...

CSDN 编辑器设置图片缩放和居中
CSDN 编辑器设置图片缩放和居中 文章目录 CSDN 编辑器设置图片缩放和居中对齐方式比例缩放 对齐方式 Markdown 编辑器插入图片的代码格式为 CSDN 的 Markdown 编辑器中插入图片,默认都是左对齐,需要设置居中对齐的话,…...
有哪些工具可以替代Gitbook?这篇文章告诉你
你是否曾经在搜索在线文档创建和共享工具时,遇到了Gitbook? Gitbook 是一个相当出色的工具,具有强大的编辑和发布功能,但也有其不足之处,如使用起来有一定的技术要求,入门门槛较高等。如果你正在寻找Gitbook的替代品&…...
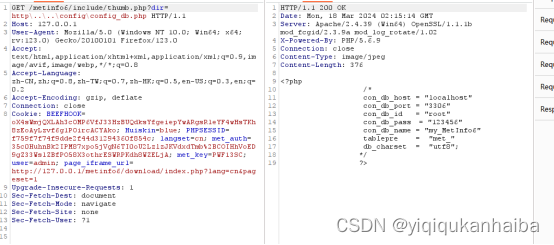
小迪安全43WEB 攻防-通用漏洞任意文件下载删除重装敏感读取黑白审计
#知识点: 1、文件操作类安全问题 2、文件下载&删除&读取 3、白盒&黑盒&探针分析 #详细点: 文件读取:基本和文件下载利用类似 文件下载:利用下载获取源码或数据库配置文件及系统敏感文件为后续出思路 …...

大模型提示学习样本量有玄机,自适应调节方法好
引言:探索文本分类中的个性化示例数量 在自然语言处理(NLP)领域,预测模型已经从零开始训练演变为使用标记数据对预训练模型进行微调。这种微调的极端形式涉及到上下文学习(In-Context Learning, ICL)&…...

Redis监控工具
Redis 是一种 NoSQL 数据库系统,以其速度、性能和灵活的数据结构而闻名。Redis 在许多领域都表现出色,包括缓存、会话管理、游戏、排行榜、实时分析、地理空间、叫车、聊天/消息、媒体流和发布/订阅应用程序。Redis 数据集完全存储在内存中,这…...

低代码表单设计器为企业数字转型强劲赋能!
想要实现数字化转型,创造流程化办公,让企业在信息高速发展的社会中抢占更多市场份额,进一步提升市场竞争力,就需要借助专业的软件平台提高效率。低代码开发平台拥有易操作、灵活、可视化的发展优势,作为一种新型的应用…...
最佳实践和准则)
【C#】Conventions(惯例)最佳实践和准则
在C#中,Conventions(惯例)是指编写代码时的一套最佳实践和准则。这些惯例旨在提高代码的可读性、一致性和可维护性。虽然这些惯例不是语言的强制规则,但遵循它们可以使你的代码更加清晰和专业。 以下是一些常见的C#编码惯例: 命名约定: 使用有意义的、描述性的名称。类名和公…...

vue3中使用cesium
vue3中使用cesium Cesium是一个开源的JavaScript库,专门用于创建3D地球和2D地图的Web应用程序。它提供了丰富的功能和工具,使得开发人员能够轻松地构建出高质量的地理空间可视化应用。 1. 安装cesium包 npm install cesium2. 复制node_modules中的Ces…...
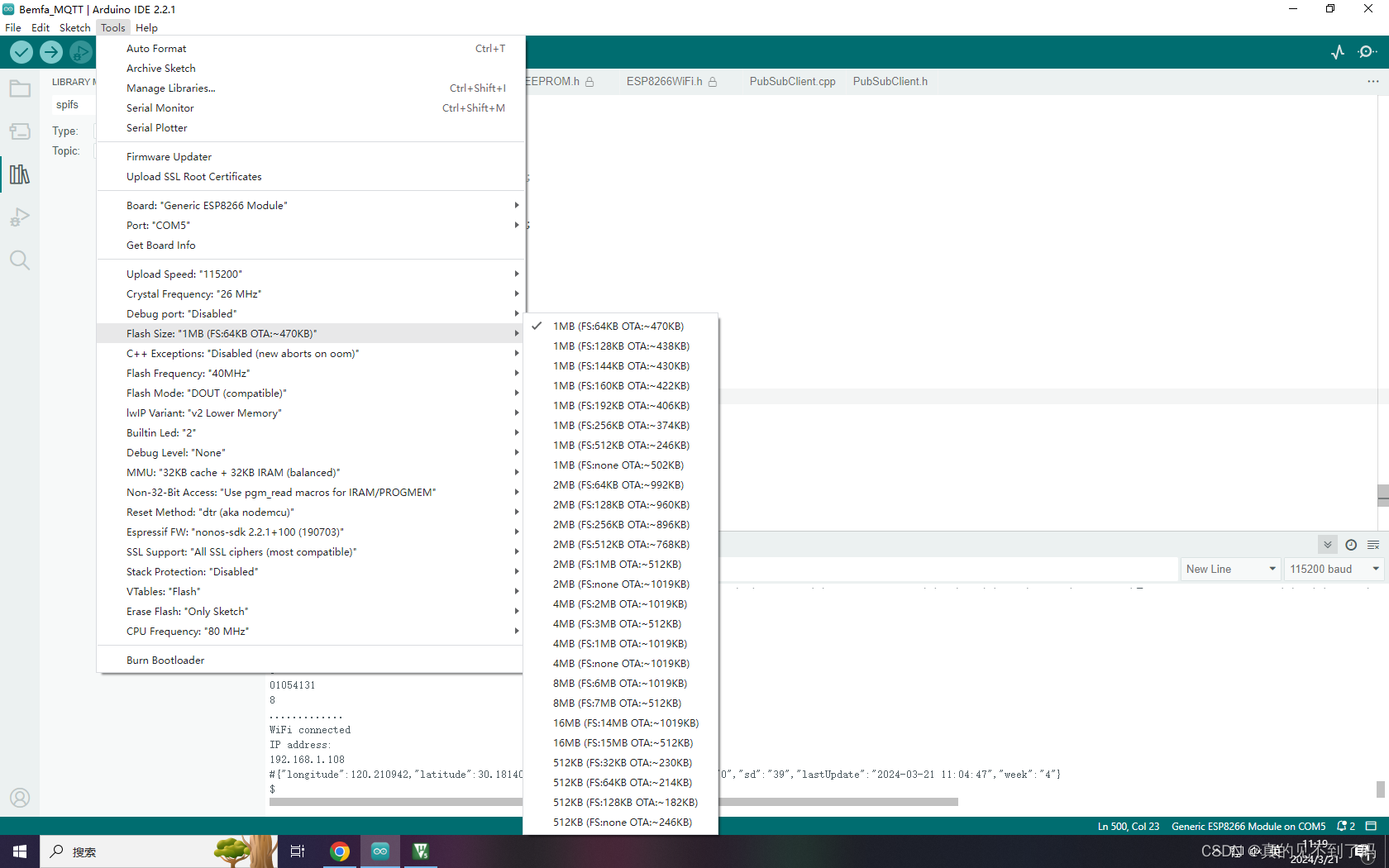
arduino ide 开发esp8266注意事项
1.引脚序列号必须是常量来定义,否则会无限重启。 #define p2 2 const int Pin2p2; pinMode(Pin2, OUTPUT); 2.关于wifi的模式,ap,sta,apsta三种模式的初始化必须放在void set_up(){}这个函数里,不能额外搞个自定义函数…...

RTC协议与算法基础 - RTP/RTCP
首先,需要说明下,webrtc的核心音视频传输是通过RTP/RTCP协议实现的,源码位于src/modules/rtp_rtcp目录下: 下面让我们对相关的内容基础进行简要分析与说明: 一、TCP与UDP协议 1.1、TCP协议 TCP为了实现数据传输的可…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...














