进阶二叉树
目录
二叉树
二叉搜索树
二叉搜索树的定义
二叉搜索树的操作
哈夫曼树
哈夫曼树的定义
哈夫曼树的构造
哈夫曼树的性质
平衡二叉树
平衡二叉树的定义:
平衡二叉树的插入调整
1.LL插入/LL旋转
2.RR插入/RR旋转
3.LR插入/LR旋转
4.RL插入/RL旋转
二叉树
二叉搜索树
二叉搜索树的定义
二叉搜索树也称二叉排序树或二叉查找树,树上任何一个结点的值,比起其左子树的值都要大,比其右子树的值都要小,并且其左右子树都是二叉搜索树

二叉搜索树的操作
1.插入:同上一篇二叉树的插入一样,插入值为x的结点
2.删除:分为三种情况:
(1)删除的结点没有子结点,就将删除的结点的父节点指向NULL
(2)删除的结点有一个子结点,就将删除的结点的父节点指向删除结点的子节点
(3)删除的节点有两个子节点,就将左子树最大的结点或右子树最小的结点替换删除的·结点
3.查找:
在树中查找值为x的结点,并返回其所在位置的地址
二叉搜索树:
最大元素一定在最右分支的端结点上
最小元素一定在最左分支的端结点上
哈夫曼树
哈夫曼树的定义
给定n个权值作为n个叶子结点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
带权路径长度(WPL):设二叉树有n个叶子结点,每个叶子结点带有权值
,从根结点到每个叶子结点的长度为
则每个叶子结点的带权路径长度之和就是:
:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
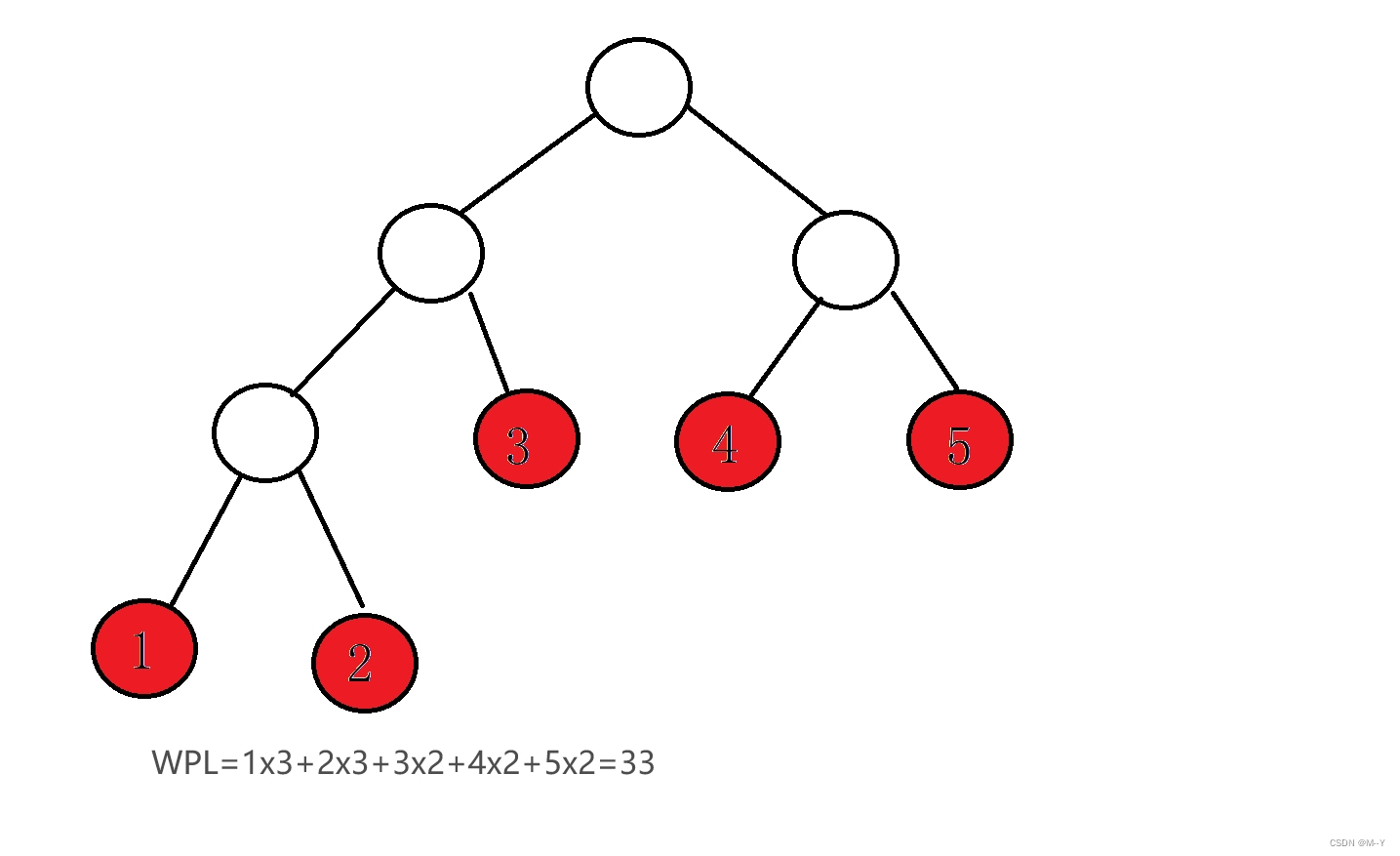
哈夫曼树的构造
每次把权值最小的两棵二叉树合并,合并得到一个新的结点,其权值是合并的两个结点的权值之和。
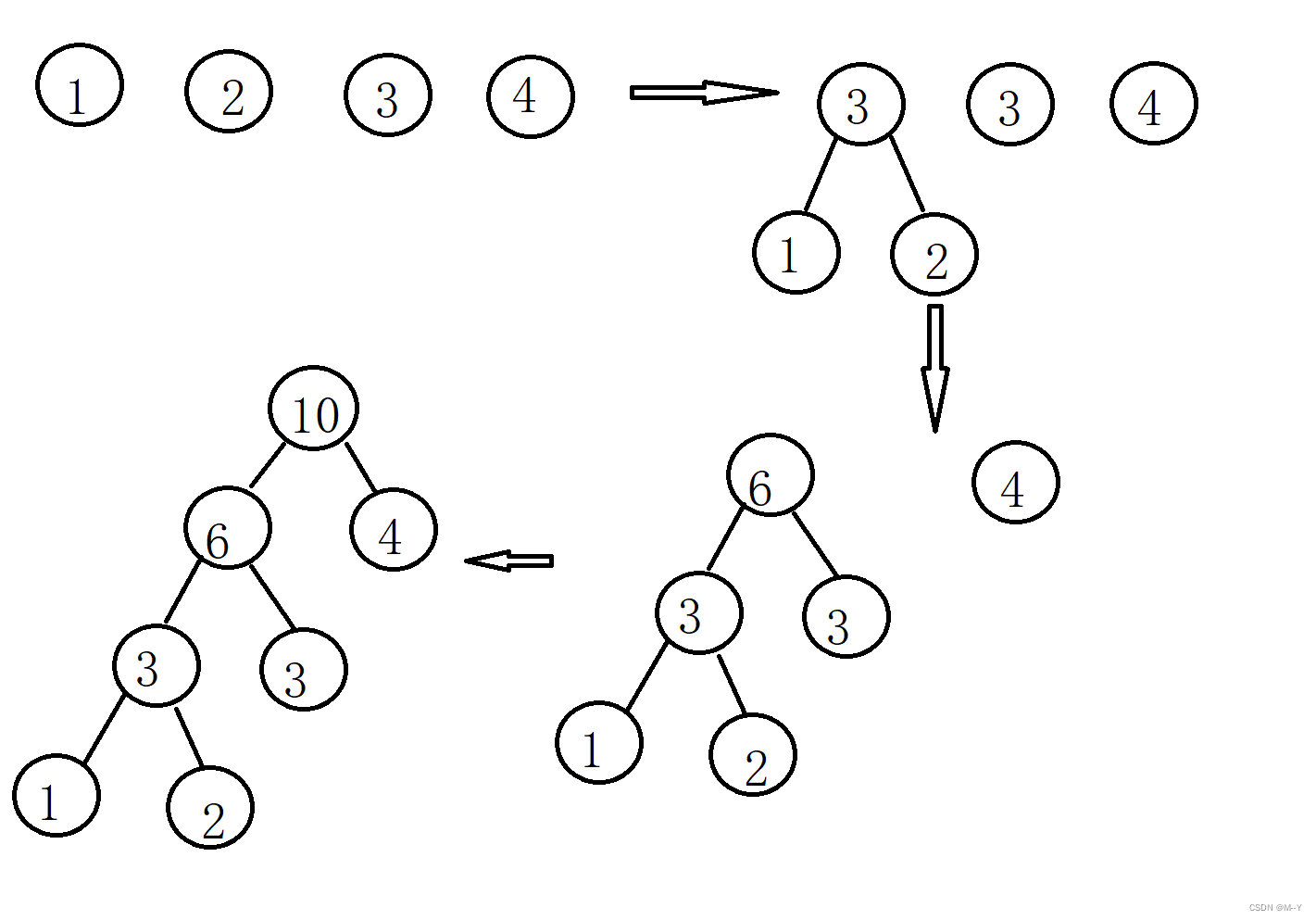
哈夫曼树的性质
1.没有度为1的结点
2.哈夫曼树的任意非叶结点互换后,任然是哈夫曼树
3.同一权值可能存在不同构造的哈夫曼树
平衡二叉树
平衡二叉树的定义:
平衡二叉树又被称做AVL树
任何一棵不空的平衡二叉树,其任意一结点的左右子树的高度差不能超过1,左右子树的高度差也被称做平衡因子(BF),BF(T)=hL-hR,hL和hR分别代表T树的左右子树高度,|BF(T)|<=1
不同的结点插入顺序,会导致生成不一样的树。则树的深度和平均查找长度ASL也会不同。
ASL = (同一层结点数量 * 结点的层次) / 结点总数
构成平衡二叉树所需的最少结点数:。
表示高度为h的平衡二叉树的最少结点数,等于前两层最少节点数之和再加1。其中n1=1,n2=2(n>=1)。
平衡二叉树的插入调整
插入的结点被称为“麻烦结点/破坏结点”。
一个结点其子树被插入新结点,该节点被陈称为“发现者/被破坏者”。
1.LL插入/LL旋转
插入的“破坏节点”,在“被破坏节点”的左子树的左子树上,因而叫LL插入。需要LL旋转(左单旋)。
LL旋转:被破坏结点为A,被破坏结点的右子树记为,被破坏结点的左子树的根节点为B,B的左、右子树记为、。将B结点提升为新的根节点,A作为B结点的右儿子,还作为A结点的右子树;还作为B结点的左子树;变为A结点的左子树。
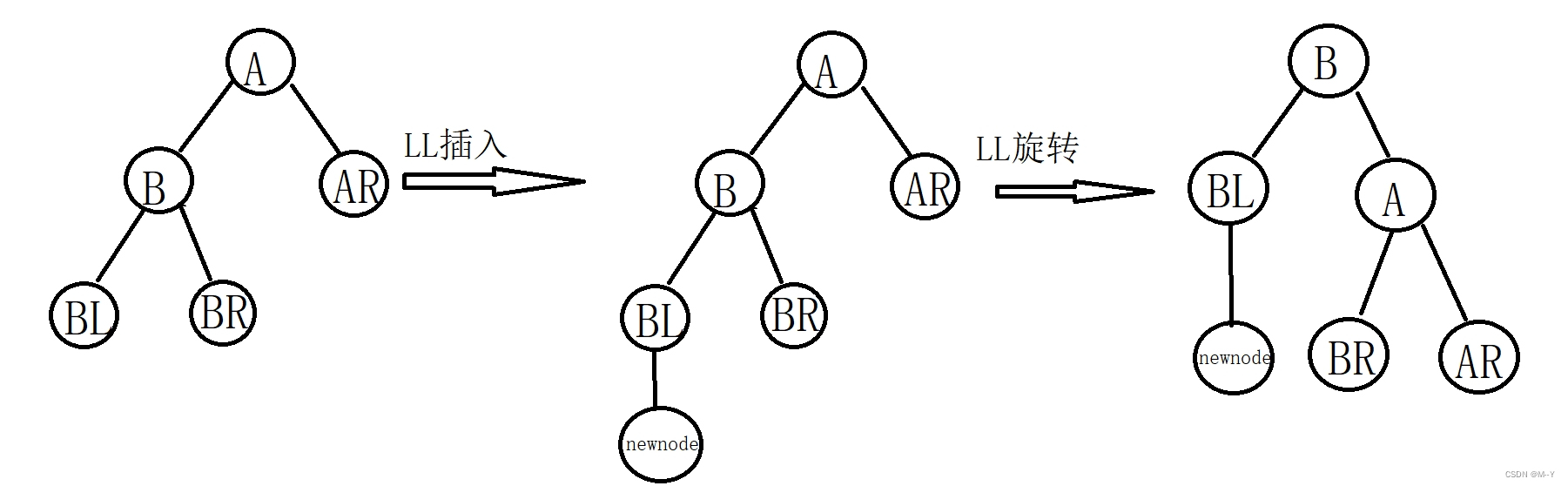
2.RR插入/RR旋转
插入的“破坏节点”,在“被破坏节点”的右子树的右子树上,因而叫RR插入。需要RR旋转(右单旋)。
RR旋转:被破坏结点为A,被破坏结点的左子树记为,被破坏结点的右子树的根节点为B,B的左、右子树记为、。将B结点提升为新的根节点,A作为B结点的左儿子,还作为A结点的左子树;还作为B结点的右子树;变为A结点的右子树。
3.LR插入/LR旋转
插入的“破坏节点”,在“被破坏节点”的左子树的右子树上,因而叫LR插入。需要LR旋转。
LR旋转:被破坏节点为A,A的左子树的根节点为B,A的右子树为;B的左子树为,B的右子树的根节点为C;C的左、右子树记为、。将C结点提升为新的根节点,B作为C结点的左儿子,A作为C的右儿子;还作为B的左子树,作为B的右子树;作为A的左子树,还作为A的右子树。
4.RL插入/RL旋转
插入的“破坏节点”,在“被破坏节点”的右子树的左子树上,因而叫RL插入。需要RL旋转。
RL旋转: 被破坏节点为A,A的左子树为,A的右子树为的根节点为B;B的左子树的根节点为C,B的右子树为;C的左、右子树记为、。将C结点提升为新的根节点,A作为C结点的左儿子,B作为C的右儿子;还作为A的左子树,作为A的右子树;作为B的左子树,还作为B的右子树。
相关文章:

进阶二叉树
目录 二叉树 二叉搜索树 二叉搜索树的定义 二叉搜索树的操作 哈夫曼树 哈夫曼树的定义 哈夫曼树的构造 哈夫曼树的性质 平衡二叉树 平衡二叉树的定义: 平衡二叉树的插入调整 1.LL插入/LL旋转 2.RR插入/RR旋转 3.LR插入/LR旋转 4.RL插入/RL旋转 二叉树…...

无人机拦截
配置yolo CUDA报错 nvcc fatal : Unsupported gpu architecture compute_30.(1)查看显卡匹配型号:https://blog.csdn.net/u013308762/article/details/121658823 (2)查看显卡:nvidia-smi -a 》NVIDIA GeF…...

CSDN 编辑器设置图片缩放和居中
CSDN 编辑器设置图片缩放和居中 文章目录 CSDN 编辑器设置图片缩放和居中对齐方式比例缩放 对齐方式 Markdown 编辑器插入图片的代码格式为 CSDN 的 Markdown 编辑器中插入图片,默认都是左对齐,需要设置居中对齐的话,…...
有哪些工具可以替代Gitbook?这篇文章告诉你
你是否曾经在搜索在线文档创建和共享工具时,遇到了Gitbook? Gitbook 是一个相当出色的工具,具有强大的编辑和发布功能,但也有其不足之处,如使用起来有一定的技术要求,入门门槛较高等。如果你正在寻找Gitbook的替代品&…...
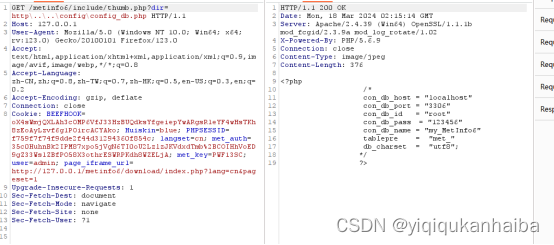
小迪安全43WEB 攻防-通用漏洞任意文件下载删除重装敏感读取黑白审计
#知识点: 1、文件操作类安全问题 2、文件下载&删除&读取 3、白盒&黑盒&探针分析 #详细点: 文件读取:基本和文件下载利用类似 文件下载:利用下载获取源码或数据库配置文件及系统敏感文件为后续出思路 …...

大模型提示学习样本量有玄机,自适应调节方法好
引言:探索文本分类中的个性化示例数量 在自然语言处理(NLP)领域,预测模型已经从零开始训练演变为使用标记数据对预训练模型进行微调。这种微调的极端形式涉及到上下文学习(In-Context Learning, ICL)&…...

Redis监控工具
Redis 是一种 NoSQL 数据库系统,以其速度、性能和灵活的数据结构而闻名。Redis 在许多领域都表现出色,包括缓存、会话管理、游戏、排行榜、实时分析、地理空间、叫车、聊天/消息、媒体流和发布/订阅应用程序。Redis 数据集完全存储在内存中,这…...

低代码表单设计器为企业数字转型强劲赋能!
想要实现数字化转型,创造流程化办公,让企业在信息高速发展的社会中抢占更多市场份额,进一步提升市场竞争力,就需要借助专业的软件平台提高效率。低代码开发平台拥有易操作、灵活、可视化的发展优势,作为一种新型的应用…...
最佳实践和准则)
【C#】Conventions(惯例)最佳实践和准则
在C#中,Conventions(惯例)是指编写代码时的一套最佳实践和准则。这些惯例旨在提高代码的可读性、一致性和可维护性。虽然这些惯例不是语言的强制规则,但遵循它们可以使你的代码更加清晰和专业。 以下是一些常见的C#编码惯例: 命名约定: 使用有意义的、描述性的名称。类名和公…...

vue3中使用cesium
vue3中使用cesium Cesium是一个开源的JavaScript库,专门用于创建3D地球和2D地图的Web应用程序。它提供了丰富的功能和工具,使得开发人员能够轻松地构建出高质量的地理空间可视化应用。 1. 安装cesium包 npm install cesium2. 复制node_modules中的Ces…...
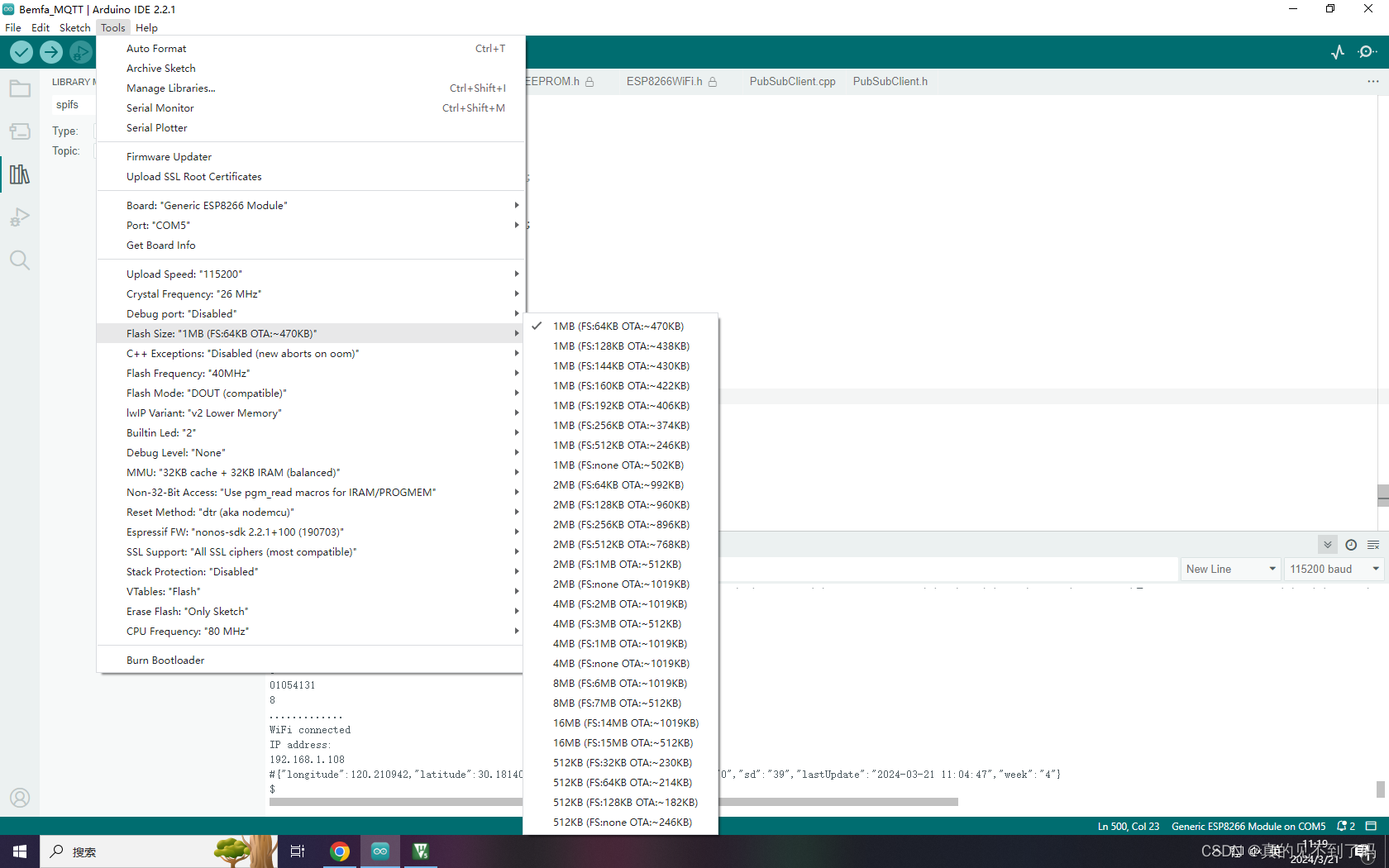
arduino ide 开发esp8266注意事项
1.引脚序列号必须是常量来定义,否则会无限重启。 #define p2 2 const int Pin2p2; pinMode(Pin2, OUTPUT); 2.关于wifi的模式,ap,sta,apsta三种模式的初始化必须放在void set_up(){}这个函数里,不能额外搞个自定义函数…...

RTC协议与算法基础 - RTP/RTCP
首先,需要说明下,webrtc的核心音视频传输是通过RTP/RTCP协议实现的,源码位于src/modules/rtp_rtcp目录下: 下面让我们对相关的内容基础进行简要分析与说明: 一、TCP与UDP协议 1.1、TCP协议 TCP为了实现数据传输的可…...
:飞机大作战)
c语言游戏实战(8):飞机大作战
前言: 飞机大作战游戏是一种非常受欢迎的射击类游戏,玩家需要控制一架战斗机在屏幕上移动,击落敌机以获得分数。本游戏使用C语言编写,旨在帮助初学者了解游戏开发的基本概念和技巧。 在开始编写代码之前,我们需要先了…...

docker 部署k8s相关命令操作
1.安装docket 可参考其他网站 2.docker ps 3.docker images 4.docker ps -all 5.docker pull openjdk:8 安装jdk8 6.docker load < jdk.tar 自己有jdk8 7.打包jar服务 ,需要依赖一个打包文件Dockerfile,如下 文件内容如下 FROM openjdk:8u275-j…...

使用Tesseract识别中文 并提高精度
1. 使用中文训练数据 在使用pytesseract进行中文文本识别时,确保安装了中文的训练数据文件。在Tesseract的安装目录下的tessdata文件夹中应包含一个名为chi_sim.traineddata(简体中文)或chi_tra.traineddata(繁体中文)…...
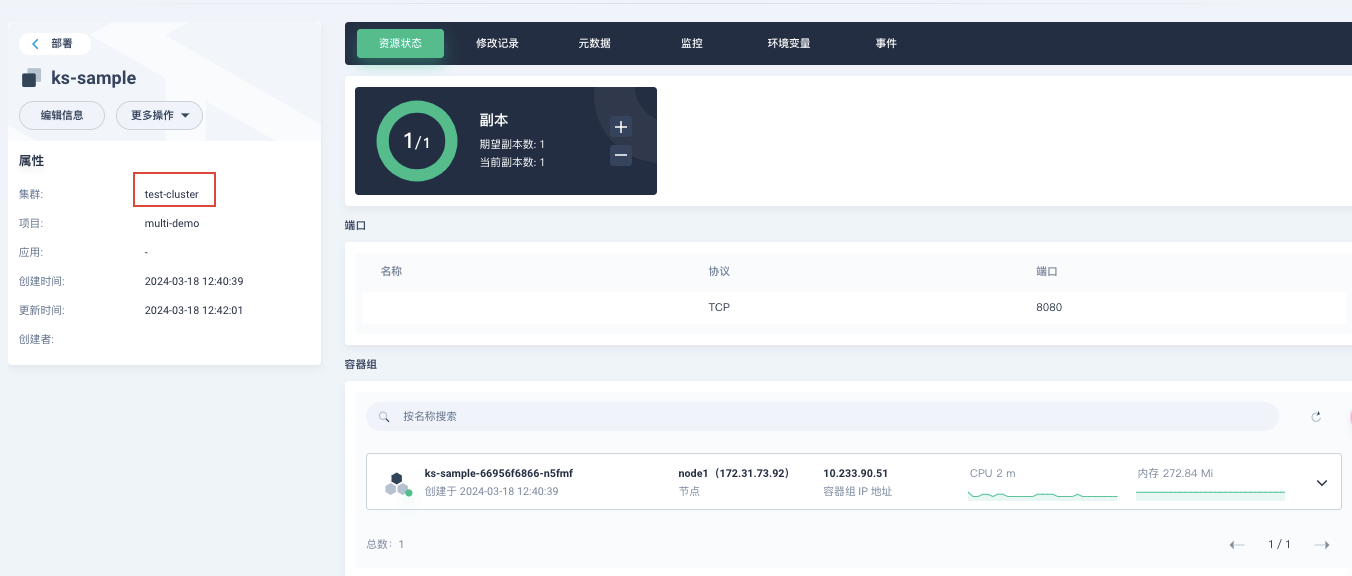
基于Jenkins + Argo 实现多集群的持续交付
作者:周靖峰,青云科技容器顾问,云原生爱好者,目前专注于 DevOps,云原生领域技术涉及 Kubernetes、KubeSphere、Argo。 前文概述 前面我们已经掌握了如何通过 Jenkins Argo CD 的方式实现单集群的持续交付,…...
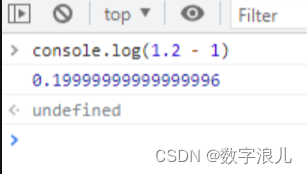
关于javascript数字精度丢失的解决办法
分析原因 众所周知,在JavaScript中计算两个十进制数的和,有时候会出现令人惊讶的结果,主要原因是计算机将数据存储为二进制所引起的,所以这并不是javascript存在的缺陷,而在其他语言中也有类似的问题。 例如下面的例子…...

每日一题 第二十一期 洛谷 组合的输出
组合的输出 题目描述 排列与组合是常用的数学方法,其中组合就是从 n n n 个元素中抽出 r r r 个元素(不分顺序且 r ≤ n r \le n r≤n),我们可以简单地将 n n n 个元素理解为自然数 1 , 2 , … , n 1,2,\dots,n 1,2,…,n&a…...

JavaScript 面试题
问题 1 // 请解释什么是 JavaScript 中的原型继承,以及原型链的概念答案 1 原型继承是 JavaScript 中实现继承的一种方式,每个对象都有一个指向另一个对象的引用,这个对象就是原型。当访问对象的属性或方法时,如果对象本身没有该…...

java输入语句scanner
在Java中,Scanner 类是 java.util 包中的一个类,它用于获取用户的输入。要使用 Scanner 类,你首先需要导入这个类,然后创建一个 Scanner 对象,通常命名为 scanner。你可以使用这个对象来读取用户从键盘输入的数据。 以…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
