力扣4寻找两个正序数组的中位数
1.实验内容
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
2.实验目的
算法的时间复杂度应该为 O(log (m+n)) 。
3.基本思路
碰到时间复杂度要求log的,肯定用二分查找,即每次在现有数据的一半中找,下一次再一半,每次循环可以将查找范围缩小一半。但是我这里用多的是双指针算法,一起查找,不需要归并数组,只需找到中位数的下标,但是复杂度仍然是O(min(m+n))
4.算法分析
首先需要通过判断`m`和`n`的大小来确定两个数组是否为空。
如果两个数组都不为空,则使用双指针法遍历两个数组,将较小的元素依次添加到动态数组`temp`中,直到找到第k+1小的元素为止。
如果其中一个数组为空,则直接将另一个非空数组赋值给`temp`。最后,根据`(m+n)%2`的值来判断中位数的位置。如果为奇数,则直接取`temp[k]`作为结果;如果为偶数,则取`temp[k]`和`temp[k-1]`的平均值作为结果。
5.实验心得
碰到时间复杂度要求log的,肯定用二分查找;但是双指针算法比普通的归并算法还是要好一些。
代码:
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {float result;int m=nums1.size();int n=nums2.size();int k=(m+n)/2;vector <int> temp;int i=0,j=0;int count=0;//如两个数组不为空,找到前k+1小数存入新数组if(m>0&& n>0){while(count<=k){if(i==m){temp.push_back(nums2[j++]);count++;continue;}if(j==n){temp.push_back(nums1[i++]);count++;continue;}temp.push_back(nums1[i]<=nums2[j]?nums1[(i++)]:nums2[(j++)]);count++;}}//其中一个数组为空的情况下else if(m==0) temp=nums2;else if(n==0) temp=nums1;//返回中位数if((m+n)%2!=0){result=temp[k];}else {result=(float(temp[k])+float(temp[k-1]))/2;}return result;}
};(PS:不是我写的)
相关文章:

力扣4寻找两个正序数组的中位数
1.实验内容 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 2.实验目的 算法的时间复杂度应该为 O(log (mn)) 。 3.基本思路 碰到时间复杂度要求log的,肯定用二分查找&…...
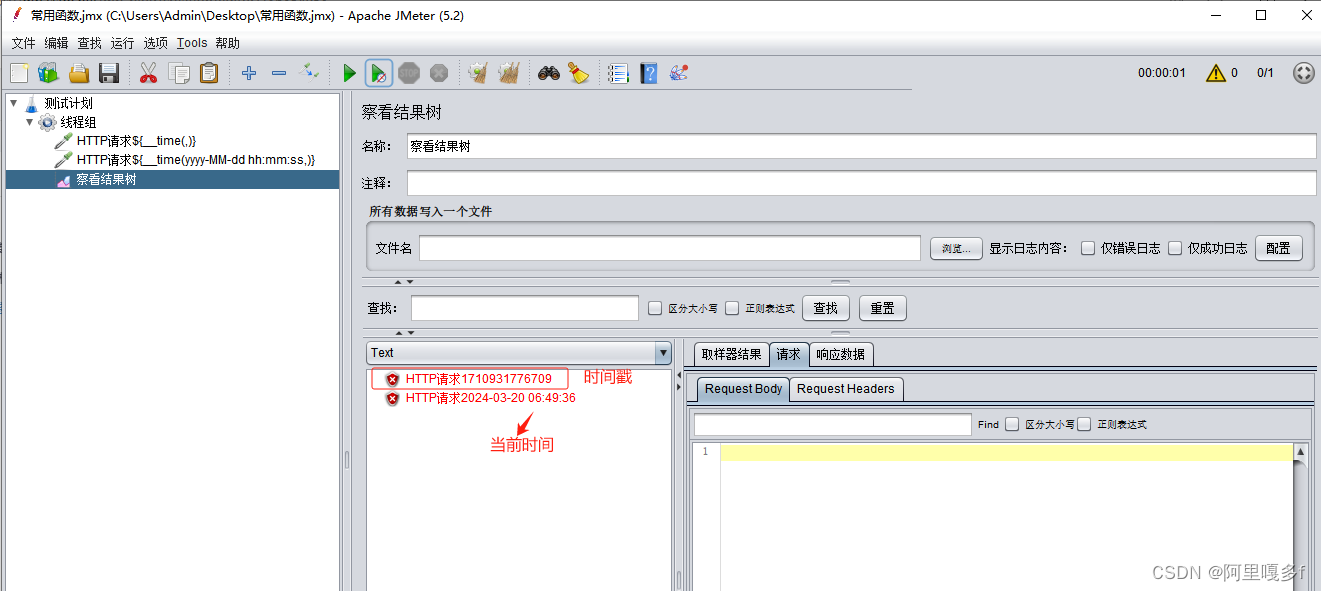
jmeter之常用函数-第六天
1.常见函数: _counter 计数器函数 TRUE(每个用户都有自己的计数器) FALSE(所有用户共用一个计数器) _Random 随机数函数 参数1:取值范围最小值(包含) 参数2:取值范围最大值(包含) _time 获取当前时间的函数 无参: 获取的是距离 1970/01/01 00:00:00 的毫秒值 参…...
原创!分解+集成思想新模型!VMD-CNN-BiGRU-Attention一键实现时间序列预测!以风速数据集为例
声明:文章是从本人公众号中复制而来,因此,想最新最快了解各类智能优化算法及其改进的朋友,可关注我的公众号:强盛机器学习,不定期会有很多免费代码分享~ 目录 数据介绍 模型流程 创新点 结果展示 部…...
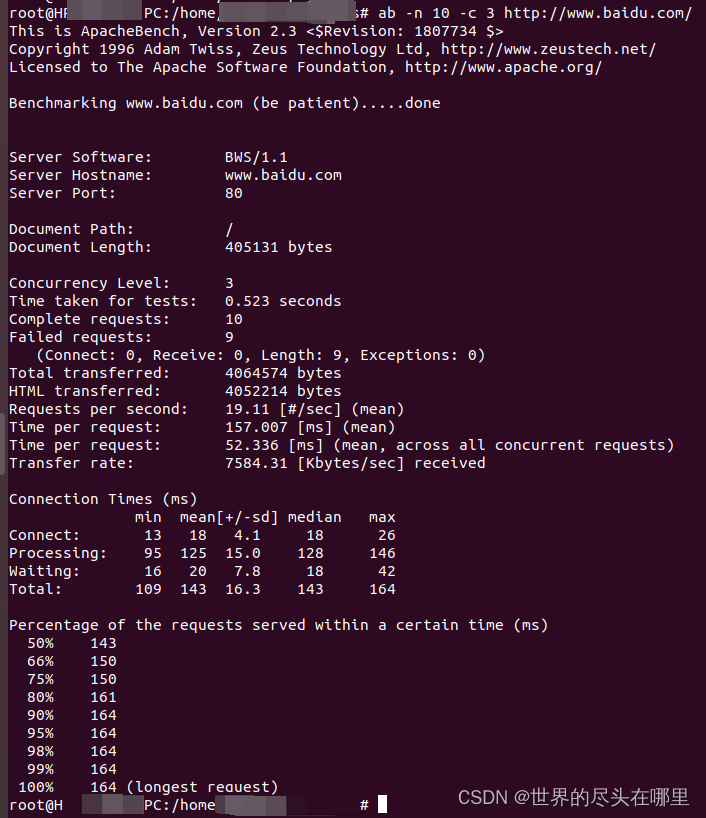
ab (Apache benchmark) - 压力/性能测试工具
Apache benchmark(ab) 安装window安装使用方法 - bin目录运行使用方法 - 任意目录运行 linux安装 基本命令介绍常用参数:输出结果分析: ab的man手册 安装 window安装 官网下载链接:https://www.apachehaus.com/cgi-bin/download…...
除了Confluence,有没有其他工具一样好用?
每个团队都需要一个协同工作工具,以更有效地管理任务、跟踪进度和分享知识。这就是Atlassian的Confluence发挥作用的地方。然而,尽管它相当强大,其昂贵的价格和复杂的界面可能会让某些用户望而却步。所以,还有其他工具可以替代Con…...
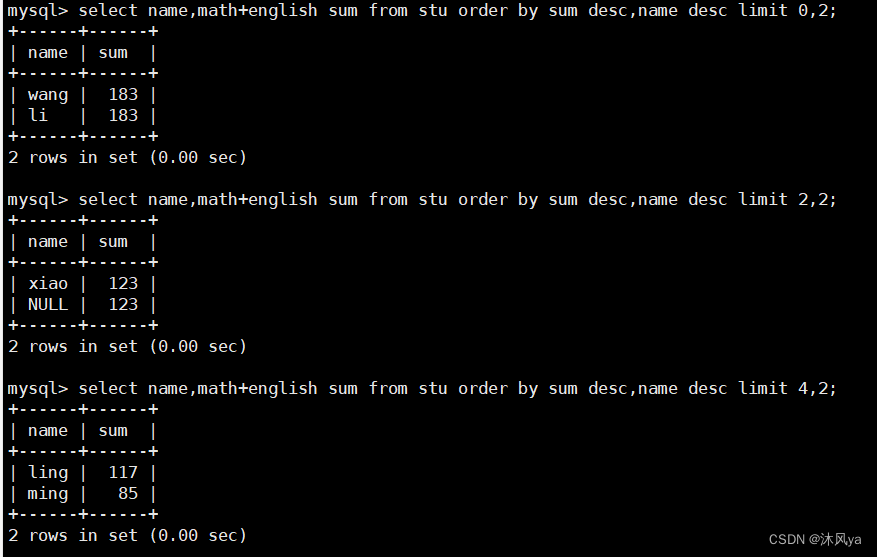
查询表中数据(全列/特定列/表达式,where子句(比较/逻辑运算符),order by子句,limit筛选分页),mysql执行顺序
目录 select 全列查询 特定列查询 用表达式查询 (as) 名字 distinct 去重 where子句 比较运算符 列数据之间的比较 编辑 别名不能参与比较 null查询 between and in ( ... , ...) 模糊匹配 逻辑运算符 order by子句 可以使用别名 总结mysql执行顺…...
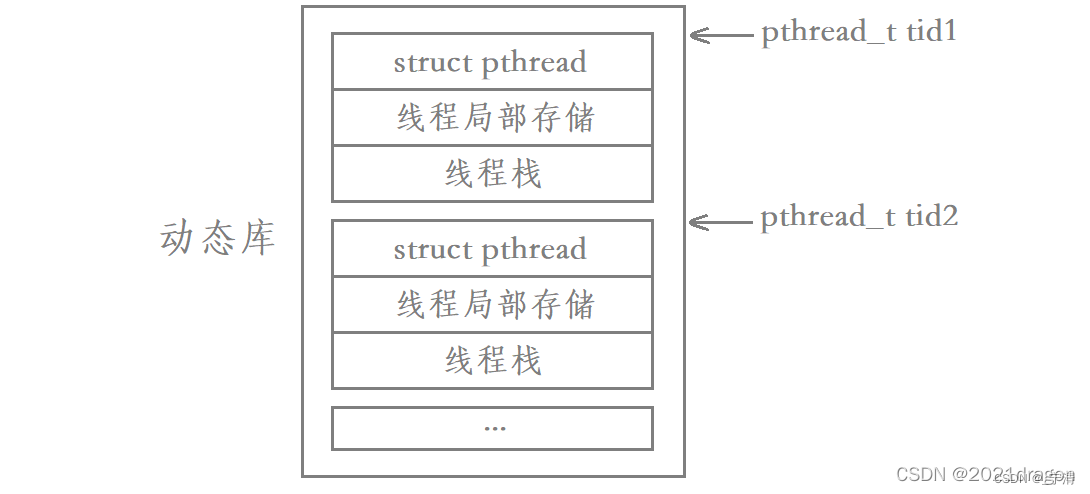
【Linux】多线程概念 | POSIX线程库
文章目录 一、线程的概念1. 什么是线程Linux下并不存在真正的多线程,而是用进程模拟的!Linux没有真正意义上的线程相关的系统调用!原生线程库pthread 2. 线程和进程的联系和区别3. 线程的优点4. 线程的缺点5. 线程异常6. 线程用途 二、二级页…...

Java Spring AOP代码3分钟快速入手
AOP Spring入门(十):Spring AOP使用讲解 - 掘金 maven的依赖: <dependency><groupId>org.springframework</groupId><artifactId>spring-aop</artifactId> </dependency> <!--aspectj支持--> <dependen…...
.NET开源快速、强大、免费的电子表格组件
今天大姚给大家分享一个.NET开源(MIT License)、快速、强大、免费的电子表格组件,支持数据格式、冻结、大纲、公式计算、图表、脚本执行等。兼容 Excel 2007 (.xlsx) 格式,支持WinForm、WPF和Android平台:ReoGrid。 项…...
docker一键部署若依前后端分离版本
比如这里把文件放到/xin/docker/jiaoZ/的目录下,jar包和下面的配置文件都放在这个文件夹下。 注意要把jar端口改为你实际启动的,映射端口也可以改为你想要的。 这里的映射端口为:nginx监听80端口,jar在8620端口,mysq…...

Java项目开发之fastjson详解
Fastjson 是由阿里巴巴公司开发的一个 Java 语言编写的高性能 JSON 处理库。它主要用于 Java 对象与 JSON 数据格式之间的转换,提供了简单易用的 API 来实现序列化(Java 对象转 JSON 字符串)和反序列化(JSON 字符串转 Java 对象&a…...

面试算法-62-盛最多水的容器
题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明:你不能倾斜容器。…...

【智能算法】海洋捕食者算法(MPA)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献 1.背景 2020年,Afshin Faramarzi 等人受到海洋生物适者生存启发,提出了海洋捕食者算法(Marine Predators Algorithm,MPA)。 2.算法原理 2.1算法思想 MPA根据模拟自然界…...
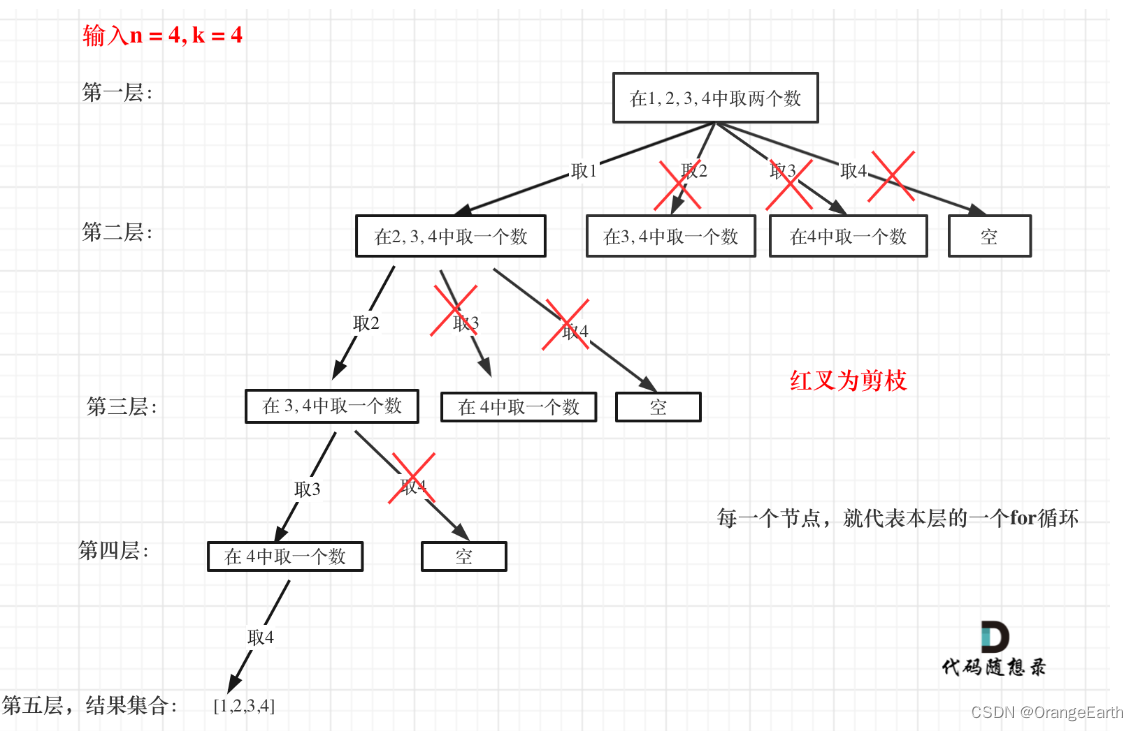
刷题DAY24 | LeetCode 77-组合
1 回溯法理论基础 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。 所以以下讲解中,回溯函数也就是递归函数,指的都是一个函数。 1.1 回溯法的效率 回溯法的性能如何呢࿰…...

Spring Boot为什么默认使用CGLIB动态代理
兼容性: 1. CGLIB 动态代理可以代理任何类型的目标类,无论它是否实现了接口;[注意的是,类被 final 修饰,那么该不可被继承,即不可被代理;同样,类中 final 修饰的方法&am…...

算法详解——Dijkstra算法
Dijkstra算法的目的是寻找单起点最短路径,其策略是贪心加非负加权队列 一、单起点最短路径问题 单起点最短路径问题:给定一个加权连通图中的特定起点,目标是找出从该起点到图中所有其他顶点的最短路径集合。需要明确的是,这里关心…...

利用GANs进行图像生成
生成对抗网络(GANs)是一种深度学习模型,由两部分组成:生成器(Generator)和判别器(Discriminator)。它们通过相互竞争来提高生成器生成高质量图像的能力。以下是如何利用GANs进行图像…...

Flutter-底部弹出框(Widget层级)
需求 支持底部弹出对话框。支持手势滑动关闭。支持在widget中嵌入引用。支持底部弹出框弹出后不影响其他操作。支持弹出框中内容固定头部和下面列表时,支持触摸头部并在列表不在头部的时候支持滑动关闭 简述 通过上面的需求可知,就是在界面中可以支持…...

聚焦两会:数字化再加速,VR全景助力制造业转型
近年来,随着信息技术、人工智能、VR虚拟现实等新兴技术的不断涌现,数字化正日益成为推动当今经济发展的新驱动力。在不久前的两会上,数字化经济和创新技术再度成为热门话题: 国务院总理李强作政府工作报告: 要深入推…...
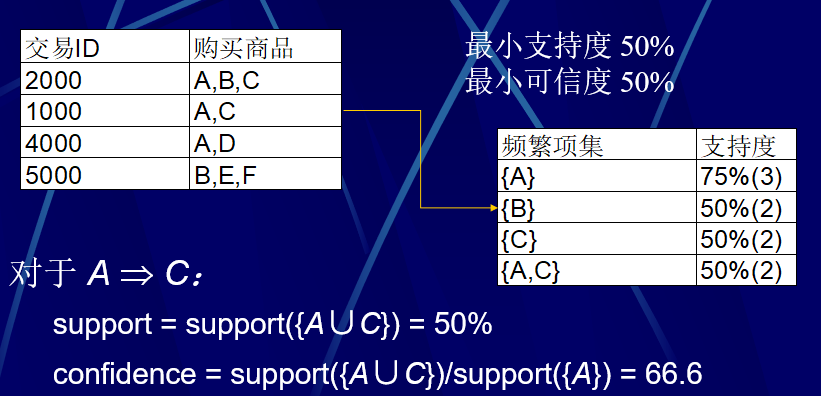
数据挖掘之关联规则
“啤酒和尿布的荣誉” 概念 项 item:单个的事物个体 ,I{i1,i2…im}是所有项的集合,|I|m是项的总数项集(item set)/模式(pattern):项的集合,包含k个项的项集称为k-项集数据集(data set)/数据库…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...
