一命通关广度优先遍历

前言
在这篇文章之前,已对非线性结构遍历的另一种方法——深度优先遍历进行了讲解,其中很多概念词都是共用的。为了更好的阅读体验,最好先在掌握或起码了解dfs的基础上,再来阅读本文章,否则因为会有很多概念词看不明白而降低阅读体验。
一命通关深度优先遍历-CSDN博客![]() https://blog.csdn.net/qq_74260823/article/details/136819359?spm=1001.2014.3001.5501
https://blog.csdn.net/qq_74260823/article/details/136819359?spm=1001.2014.3001.5501
广度优先遍历
简介
与dfs不同,bfs是先遍历完一层的所有结点,再往下一层进发。bfs先踏完第一步能到达的所有结点,然后再遍历第二步才可以到达的结点,一直遍历到最远才可以到达的结点,完成遍历。
- 但是,同一个结点可能会在两个范围中:

- 也可能会有回头路:

不过,所有的结点只能被遍历一次,所以,大部分bfs问题,都需要配有一个标记数组。
实现方法
我们想知道第二步才可以到达的结点,最直接的想法就是在找到所有第一步就能到达的情况下,再走一步,就是第二步才可以到达的结点。为了实现这个思想,即通过上一层去找下一层的结点,最直接的实现方法就是采用两个数组:

我们遍历上层数组的所有元素,然后通过这些元素找到他们相邻的结点,就是下一层元素的所有元素。
然后,继续往下遍历,将上层数组清空,与下层数组交换,如此反复交替,一直到走到最后一层。
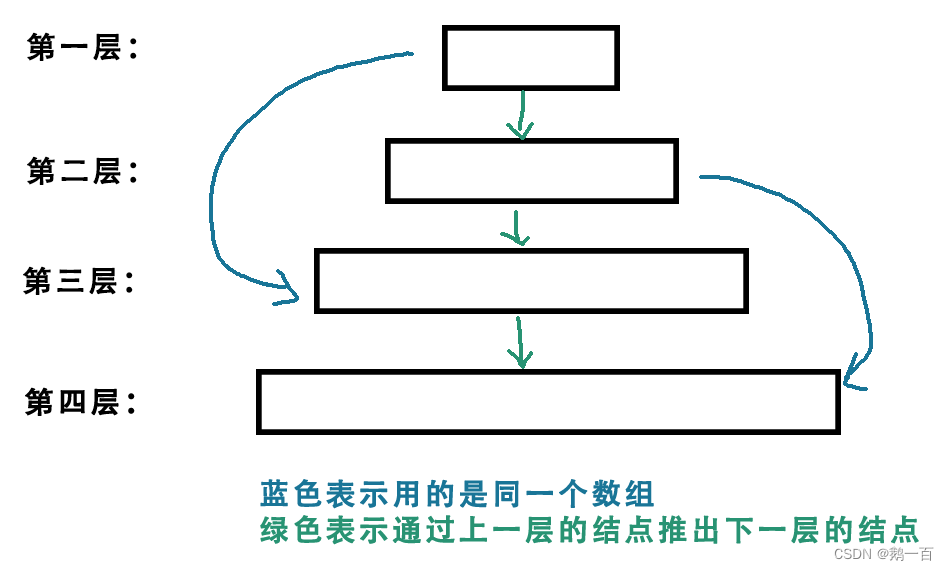
不过,这种方法可以优化成一个队列实现:

将上一层的元素弹出的同时,将下一层的元素带入队列尾,这种方法思想在二叉树的层序遍历中已经详细讲过了,就不再重复说明了。
因为解题思路和公式非常非常套路化,所以直接上题目:
200. 岛屿数量 - 力扣(LeetCode)

简单翻译一下题目,就是找到有几个不挨着的1区块。
而解法也很简单,我们遍历所有元素,当遇到1时,就采用bfs或者dfs将相邻的1全部标记一下,我们这里用bfs来实现。
首先还是在dfs里一模一样的:
- 位移数组drow和dcol
- 主函数部分,遍历每个源头
- 判断边界条件
而唯一和dfs不一样的,也只不过是dfs和bfs函数中的一小部分
class Solution {int m,n;vector<vector<bool>> record;int drow[4]={1,-1,0,0};int dcol[4]={0,0,1,-1};int ret;//与dfs一模一样typedef pair<int,int> ii;
public:void bfs(vector<vector<char>>& grid,int i,int j){queue<ii> que;que.push({i,j});record[i][j]=true;while(!que.empty()){auto [row,col]=que.front();que.pop();for(int i=0;i<4;i++){int newrow=row+drow[i];int newcol=col+dcol[i];if(newrow>=0&&newrow<m&&newcol>=0&&newcol<n&&record[newrow][newcol]==false&&grid[newrow][newcol]=='1')//与dfs一模一样{que.push({newrow,newcol});record[newrow][newcol]=true;}}}}int numIslands(vector<vector<char>>& grid) {m=grid.size();n=grid[0].size();record.resize(m,vector<bool>(n));for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(record[i][j]==false&&grid[i][j]=='1'){bfs(grid,i,j);ret++;}}}return ret;}//整个主函数也与dfs一模一样
};所以,bfs的公式也很明了,和dfs大差不差:
公式
class Solution {int dx[4] = { 0,0,1,-1 };int dy[4] = { 1,-1,0,0 };//方向数组vector<vector<bool>> record;//标记数组int m, n;//矩阵长宽typedef pair<int, int> ii;
public:void bfs(vector<vector<int>>& grid, int i, int j){queue<ii> que;//创建bfs用的队列que.push({ i , j });//将源头插入队列中while (!que.empty()){auto [row, col] = que.front();//取队头元素for (int i = 0; i < 4; i++){int nextrow = row + dy[i];int nextcol = col + dx[i];//新的坐标if (nextrow >= 0 && nextrow < m && nextcol >= 0 && nextcol < n//不越界&& record[nextrow][nextcol] == false//没有走回头路&& grid[nextrow][nextcol]...)//满足题目要求{record[nextrow][nextcol] = true;que.push({ nextrow,nextcol });}}}}... main(vector<vector<int>>& grid) {m = grid.size();n = grid[0].size();record.resize(m, vector<bool>(n));//遍历每一个源头for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (record[i][j]==false&&grid[i][j] != 0){record[i][j] = true;bfs(grid, i, j);}}}}
};
相关文章:

一命通关广度优先遍历
前言 在这篇文章之前,已对非线性结构遍历的另一种方法——深度优先遍历进行了讲解,其中很多概念词都是共用的。为了更好的阅读体验,最好先在掌握或起码了解dfs的基础上,再来阅读本文章,否则因为会有很多概念词看不明白…...

力扣4寻找两个正序数组的中位数
1.实验内容 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 2.实验目的 算法的时间复杂度应该为 O(log (mn)) 。 3.基本思路 碰到时间复杂度要求log的,肯定用二分查找&…...
jmeter之常用函数-第六天
1.常见函数: _counter 计数器函数 TRUE(每个用户都有自己的计数器) FALSE(所有用户共用一个计数器) _Random 随机数函数 参数1:取值范围最小值(包含) 参数2:取值范围最大值(包含) _time 获取当前时间的函数 无参: 获取的是距离 1970/01/01 00:00:00 的毫秒值 参…...
原创!分解+集成思想新模型!VMD-CNN-BiGRU-Attention一键实现时间序列预测!以风速数据集为例
声明:文章是从本人公众号中复制而来,因此,想最新最快了解各类智能优化算法及其改进的朋友,可关注我的公众号:强盛机器学习,不定期会有很多免费代码分享~ 目录 数据介绍 模型流程 创新点 结果展示 部…...
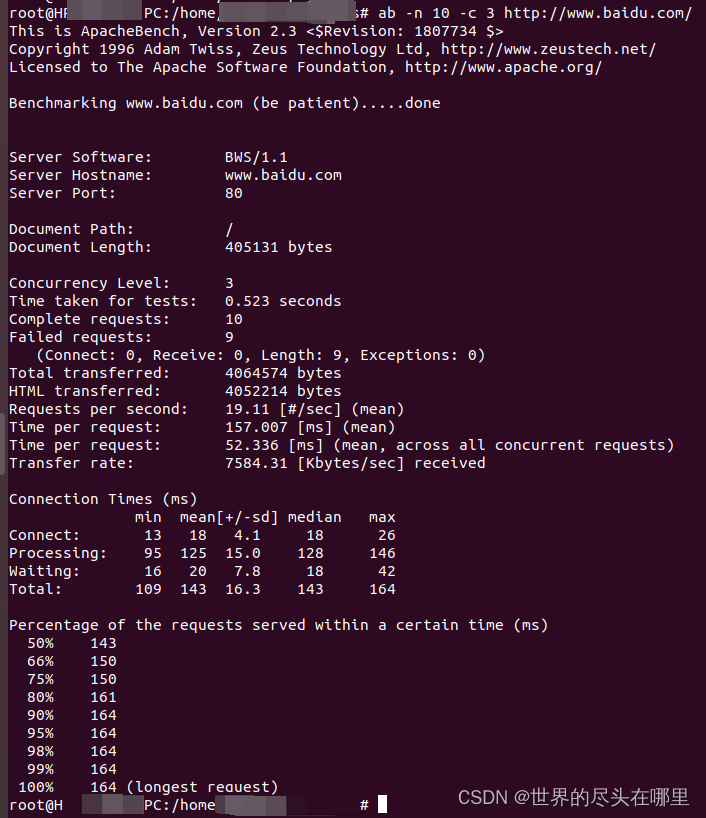
ab (Apache benchmark) - 压力/性能测试工具
Apache benchmark(ab) 安装window安装使用方法 - bin目录运行使用方法 - 任意目录运行 linux安装 基本命令介绍常用参数:输出结果分析: ab的man手册 安装 window安装 官网下载链接:https://www.apachehaus.com/cgi-bin/download…...
除了Confluence,有没有其他工具一样好用?
每个团队都需要一个协同工作工具,以更有效地管理任务、跟踪进度和分享知识。这就是Atlassian的Confluence发挥作用的地方。然而,尽管它相当强大,其昂贵的价格和复杂的界面可能会让某些用户望而却步。所以,还有其他工具可以替代Con…...
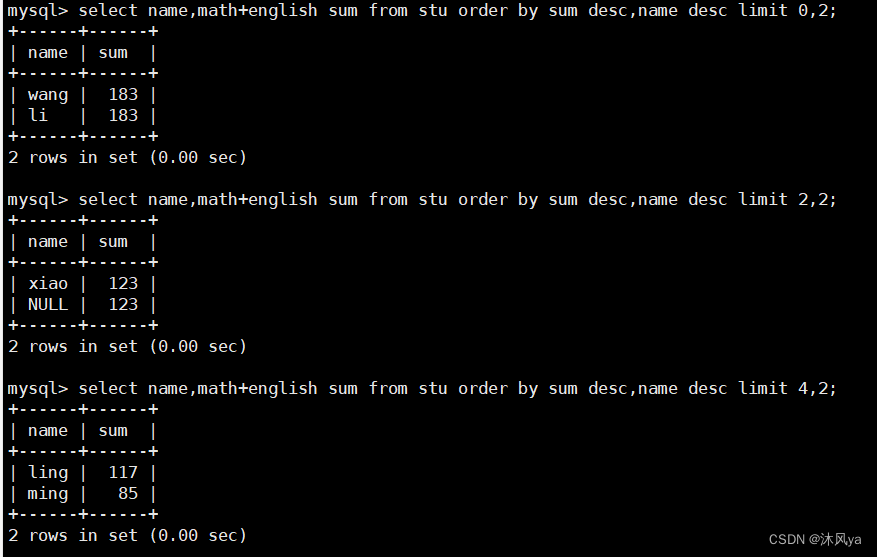
查询表中数据(全列/特定列/表达式,where子句(比较/逻辑运算符),order by子句,limit筛选分页),mysql执行顺序
目录 select 全列查询 特定列查询 用表达式查询 (as) 名字 distinct 去重 where子句 比较运算符 列数据之间的比较 编辑 别名不能参与比较 null查询 between and in ( ... , ...) 模糊匹配 逻辑运算符 order by子句 可以使用别名 总结mysql执行顺…...
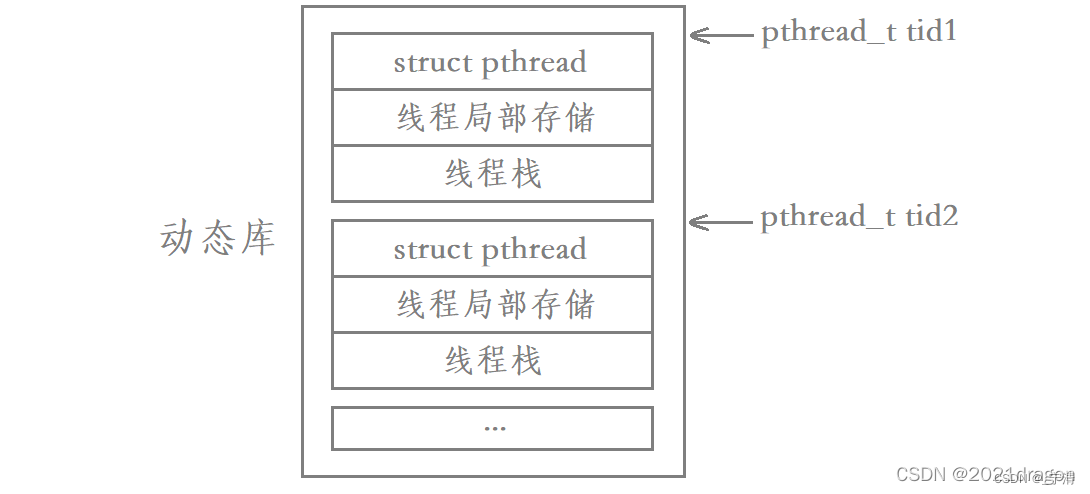
【Linux】多线程概念 | POSIX线程库
文章目录 一、线程的概念1. 什么是线程Linux下并不存在真正的多线程,而是用进程模拟的!Linux没有真正意义上的线程相关的系统调用!原生线程库pthread 2. 线程和进程的联系和区别3. 线程的优点4. 线程的缺点5. 线程异常6. 线程用途 二、二级页…...

Java Spring AOP代码3分钟快速入手
AOP Spring入门(十):Spring AOP使用讲解 - 掘金 maven的依赖: <dependency><groupId>org.springframework</groupId><artifactId>spring-aop</artifactId> </dependency> <!--aspectj支持--> <dependen…...
.NET开源快速、强大、免费的电子表格组件
今天大姚给大家分享一个.NET开源(MIT License)、快速、强大、免费的电子表格组件,支持数据格式、冻结、大纲、公式计算、图表、脚本执行等。兼容 Excel 2007 (.xlsx) 格式,支持WinForm、WPF和Android平台:ReoGrid。 项…...
docker一键部署若依前后端分离版本
比如这里把文件放到/xin/docker/jiaoZ/的目录下,jar包和下面的配置文件都放在这个文件夹下。 注意要把jar端口改为你实际启动的,映射端口也可以改为你想要的。 这里的映射端口为:nginx监听80端口,jar在8620端口,mysq…...

Java项目开发之fastjson详解
Fastjson 是由阿里巴巴公司开发的一个 Java 语言编写的高性能 JSON 处理库。它主要用于 Java 对象与 JSON 数据格式之间的转换,提供了简单易用的 API 来实现序列化(Java 对象转 JSON 字符串)和反序列化(JSON 字符串转 Java 对象&a…...

面试算法-62-盛最多水的容器
题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明:你不能倾斜容器。…...

【智能算法】海洋捕食者算法(MPA)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献 1.背景 2020年,Afshin Faramarzi 等人受到海洋生物适者生存启发,提出了海洋捕食者算法(Marine Predators Algorithm,MPA)。 2.算法原理 2.1算法思想 MPA根据模拟自然界…...
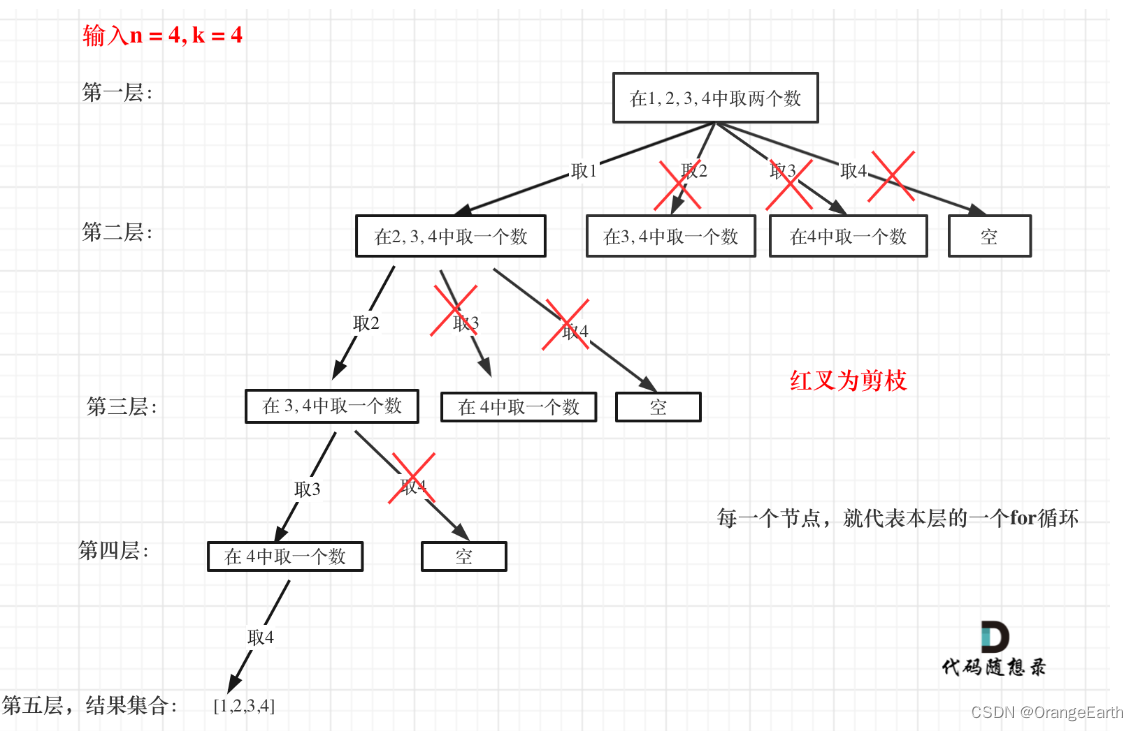
刷题DAY24 | LeetCode 77-组合
1 回溯法理论基础 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。 所以以下讲解中,回溯函数也就是递归函数,指的都是一个函数。 1.1 回溯法的效率 回溯法的性能如何呢࿰…...

Spring Boot为什么默认使用CGLIB动态代理
兼容性: 1. CGLIB 动态代理可以代理任何类型的目标类,无论它是否实现了接口;[注意的是,类被 final 修饰,那么该不可被继承,即不可被代理;同样,类中 final 修饰的方法&am…...

算法详解——Dijkstra算法
Dijkstra算法的目的是寻找单起点最短路径,其策略是贪心加非负加权队列 一、单起点最短路径问题 单起点最短路径问题:给定一个加权连通图中的特定起点,目标是找出从该起点到图中所有其他顶点的最短路径集合。需要明确的是,这里关心…...

利用GANs进行图像生成
生成对抗网络(GANs)是一种深度学习模型,由两部分组成:生成器(Generator)和判别器(Discriminator)。它们通过相互竞争来提高生成器生成高质量图像的能力。以下是如何利用GANs进行图像…...

Flutter-底部弹出框(Widget层级)
需求 支持底部弹出对话框。支持手势滑动关闭。支持在widget中嵌入引用。支持底部弹出框弹出后不影响其他操作。支持弹出框中内容固定头部和下面列表时,支持触摸头部并在列表不在头部的时候支持滑动关闭 简述 通过上面的需求可知,就是在界面中可以支持…...

聚焦两会:数字化再加速,VR全景助力制造业转型
近年来,随着信息技术、人工智能、VR虚拟现实等新兴技术的不断涌现,数字化正日益成为推动当今经济发展的新驱动力。在不久前的两会上,数字化经济和创新技术再度成为热门话题: 国务院总理李强作政府工作报告: 要深入推…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
