python统计分析——t分布、卡方分布、F分布
参考资料:python统计分析【托马斯】
一些常见的连续型分布和正态分布分布关系紧密。
t分布:正态分布的总体中,样本均值的分布。通常用于小样本数且真实的均值/标准差不知道的情况。
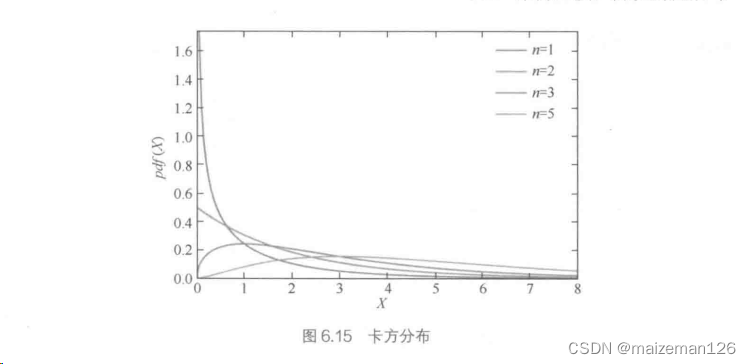
卡方分布:用于描述正态分布数据的变异程度。
F分布:用于比较两组正态分布的变异程度。
1、t分布
1908年,在都柏林的吉尼斯啤酒厂工作的W. S. Gosset被小样本的问题所在吸引,比如说大麦的化学性质,其样本量经常低至3左右。由于这些测量中,均值的真实方差并不知道,所以必须用均值的标准误来近似。样本均值和标准误之间的比例服从一个未知的分布,直到笔名为“Student”的Gosset解决了这个问题。对应的分布就是t分布,并在大样本量时收敛于正态分布。由于Gosset的笔名叫“Student”,该分布又叫做“Student”分布。
由于大多数情况下,总体的均值和方差是未知的,我们在分析样本数据时一般都是处理t分布。t统计量可表示为:
t分布的一个非常常见的应用就是计算均值的置信区间。95%置信区间(CI)的宽度,也就是说,这个区间在95%的情况下包含了真实的均值,该置信区间和包含95%样本均值的总体均值的宽度相同。
下面的例子展示了对于n=20来说,如何计算t值并求其95%置信区间。95%置信区间的下限是大于分布2.5%的值;而其上限值是小于分布的97.5%的值。这些只可以通过百分点函数或逆生存函数获得。作为对比,我们也计算出正态分布对应的值。
# 导入库
import numpy as np
from scipy import stats
# 设置样本容量
n=20
# 计算自由度
df=n-1
# 设置显著性水平
alpha=0.05
# 利用逆生存函数获取t分布对应的位点值
stats.t(df).isf(alpha/2)
# 正态分布对应的位点值
stats.norm.isf(alpha/2)
# 当然在python可以用一行代码获得执行区间
# 比如计算样本容量为20,样本均值为10,标准差为5对应的均值置信区间
ci=stats.t.interval(alpha,df=19,loc=10,scale=10/5)
ci2、卡方分布
卡方分布以一种很简单的方式和正态分布产生关联:如果一个随机变量X服从正态分布,那么X^2服从卡方分布,其自由度是1。n个独立的标准正态随机变量平方和有n个自由度。
示例:
一个药品制造商街道一个药品订单,需要发货的药片的标准差为σ=0.05。从下一批次的药品开始,n=13的随机样本的重量为3.04g、2.94g、3.01g、3.00g、2.94g、2.91g、3.02g、3.04g、3.09g、2.95g、2.99g、3.10g、3.02g。
问:标准差是否高于准许值?
答:由于卡方分布描述了来自标准正态分布的随机变量的平方和,我们不得不在计算相应的CDF值之前正态化我们的数据:
解释:如果这一批药来自标准差为0.05的一个分布,那么得到一个大于等于我们观察到的卡方值的可能性大约是19%。所以这并不反常。换句话说,这批药符合期望的标准差。
代码如下:
# 导入库
import numpy as np
from scipy import stats
# 录入数据
data=np.r_[3.04,2.94,3.01,3.00,2.94,2.91,3.02,3.04,3.09,2.95,2.99,3.10,3.02]
# 设置目标标准差
sigma=0.05
# 设置卡方分布
chi2Dist=stats.chi2(len(data)-1)
# 计算统计量
statistic=sum(((data-np.mean(data))/sigma)**2)
# 计算统计量对应的生存函数
chi2Dist.sf(statistic)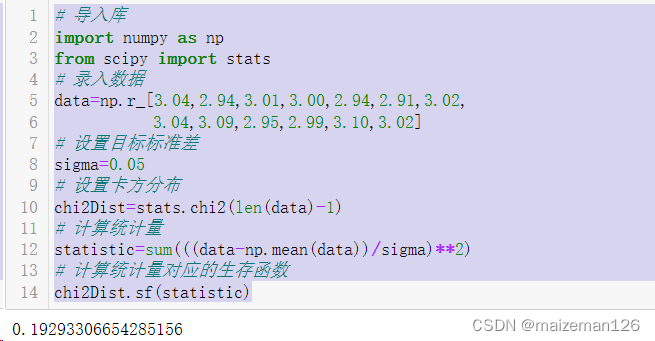
3、F分布
该分布以Ronald Fisher先生的名字命名,他发明了F分布来决定ANOVA(方差分析)中的关键值。
如果想要调查两个组别是否具有相同的方差,我们就必须计算两组标准差平方的比值:
其中,S_x是第一个样本的样本标准差,S_y是第二个样本的样本标准差。
这个统计量的分布就是F分布。在ANOVA中的应用来说,F分布的临界值经常通过3个变量计算得到:
①ANOVA分子自由度,
②ANOVA分母自由度,
③显著性水平。
ANOVA比较了两个不同样本之间的方差大小,是用大的方差除以小的方差来完成的。最终的F统计量的公式如下:
其中和
分别是样本1和样本2的卡方统计量,r1和r2是他们的自由度。
示例
我们想比较两种测量眼睛运动的方法的精确度。这两种方法有不同的精确度和准确度。精确度描述了真实值和测量值之间的差异,而准确度由测量的变异程度决定。我们想用这个检验来决定两种方法的准确度是否相同,还是其中一种方法比另一种方法更准确。
方法1数据:[20.7,20.3,20.3,20.3,20.7,19.9,19.9,19.9,20.3,20.3,19.7,20.3]
方法2数据:[19.7,19.4,20.1,18.6,18.8,20.2,18.7,19.0]
计算代码如下:
# 导入库
import numpy as np
from scipy import stats
# 录入数据
method1=np.array([20.7,20.3,20.3,20.3,20.7,19.9,19.9,19.9,20.3,20.3,19.7,20.3])
method2=np.array([19.7,19.4,20.1,18.6,18.8,20.2,18.7,19.0])
# 计算f值
f_val=np.var(method1,ddof=1)/np.var(method2,ddof=1)
# 设置F分布
fd=stats.f(len(method1)-1,len(method2)-1)
p_onetail=fd.cdf(f_val)
print(p_onetail)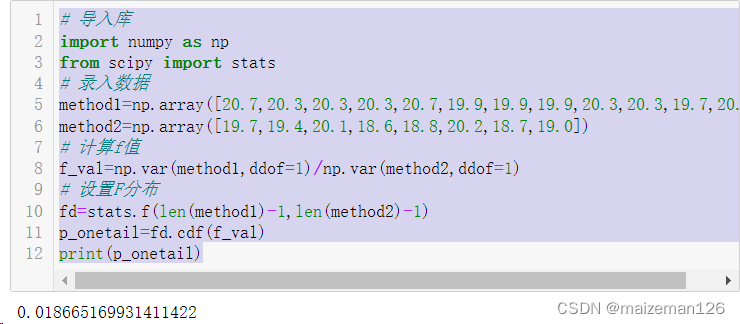
代码运行结果可知,p=0.019,所以我们拒绝原假设(两种方法有相同的准确度)。
相关文章:

python统计分析——t分布、卡方分布、F分布
参考资料:python统计分析【托马斯】 一些常见的连续型分布和正态分布分布关系紧密。 t分布:正态分布的总体中,样本均值的分布。通常用于小样本数且真实的均值/标准差不知道的情况。 卡方分布:用于描述正态分布数据的变异程度。 F分…...
onlyoffice创建excel文档
前提 安装好onlyoffice然后尝试api开发入门 编写代码 <html> <head><meta charset"UTF-8"><meta name"viewport"content"widthdevice-width, user-scalableno, initial-scale1.0, maximum-scale1.0, minimum-scale1.0"&…...

交通事故档案管理系统|基于JSP技术+ Mysql+Java+Tomcat的交通事故档案管理系统设计与实现(可运行源码+数据库+设计文档)
推荐阅读100套最新项目 最新ssmjava项目文档视频演示可运行源码分享 最新jspjava项目文档视频演示可运行源码分享 最新Spring Boot项目文档视频演示可运行源码分享 2024年56套包含java,ssm,springboot的平台设计与实现项目系统开发资源(可…...
Chrome 114 带着侧边栏扩展来了
效果展示 manifest.json {"manifest_version": 3,"name": "ChatGPT学习","version": "0.0.2","description": "ChatGPT,GPT-4,Claude3,Midjourney,Stable Diffusion,AI,人工智能,AI","icons"…...

【论文笔记】RobotGPT: Robot Manipulation Learning From ChatGPT
【论文笔记】RobotGPT: Robot Manipulation Learning From ChatGPT 文章目录 【论文笔记】RobotGPT: Robot Manipulation Learning From ChatGPTAbstractI. INTRODUCTIONII. RELATED WORK1. LLMs for Robotics2. Robot Learning III. METHODOLOGY1. ChatGPT Prompts for Robot …...

深度学习 Lecture 4 Adam算法、全连接层与卷积层的区别、图计算和反向传播
一、Adam算法(自适应矩估计) 全名:Adapative Moment Estimation 目的:最小化代价函数(和梯度下降一样) 本质:根据更新学习率后的情况自动更新学习率的值(可能是自动增大,也可能是…...
uniApp中使用小程序XR-Frame创建3D场景(1)环境搭建
1.XR-Frame简介 XR-Frame作为微信小程序官方推出的3D框架,是目前所有小程序平台中3D效果最好的一个,由于其本身针对微信小程序做了优化,在性能方面比其他第三方库都要高很多。 2.与Three.js的区别 做3D小程序的同学们对Three.js一定不陌生…...

AI基础知识(4)--贝叶斯分类器
1.什么是贝叶斯判定准则(Bayes decision rule)?什么是贝叶斯最优分类器(Bayes optimal classifier)? 贝叶斯判定准则:为最小化总体风险,只需在每个样本上选择那个能使条件风险最小的…...

填补市场空白,Apache TsFile 如何重新定义时序数据管理
欢迎全球开发者参与到 Apache TsFile 项目中。 刚刚过去的 2023 年,国产开源技术再次获得国际认可。 2023 年 11 月 15 日,经全球最大的开源软件基金会 ASF 董事会投票决议,时序数据文件格式 TsFile 正式通过,直接晋升为 Apache T…...

Docker 笔记(七)--打包软件生成镜像
目录 1. 背景2. 参考3. 文档3.1 使用docker container commit命令构建镜像3.1.1 [Docker官方文档-docker container commit](https://docs.docker.com/reference/cli/docker/container/commit/)Description(概述)Options(选项)Exa…...
图论06-飞地的数量(Java)
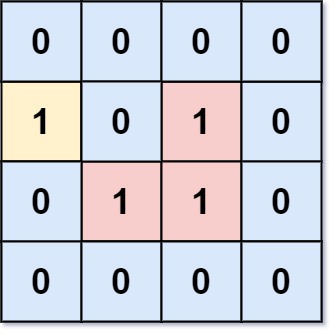
6.飞地的数量 题目描述 给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。 一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右)的陆地单元格或跨过 grid 的边界。 返回网格中 无法…...

Java设计模式之单例设计模式
单例设计模式就是保证整个软件系统中,某个类只能存在一个对象实例,并且该类只提供一个取得该对象的方法。 单例设计模式包括两种:饿汉式和懒汉式。 饿汉式: 含义: 在类加载时就创建并初始化单例对象。这种方式确保了…...

多维时序 | MATLAB实现BiTCN-selfAttention自注意力机制结合双向时间卷积神经网络多变量时间序列预测
多维时序 | MATLAB实现BiTCN-selfAttention自注意力机制结合双向时间卷积神经网络多变量时间序列预测 目录 多维时序 | MATLAB实现BiTCN-selfAttention自注意力机制结合双向时间卷积神经网络多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.M…...

深入了解Android垃圾回收机制
文章目录 一、内存分配二、垃圾回收触发条件三、GC算法3.1 Dalvik虚拟机的GC算法3.2 ART的GC算法 四、优化GC性能五、监控GC耗时情况六、总结 在Android应用开发中,内存管理和垃圾回收(GC)对于应用性能和稳定性至关重要。理解GC机制有助于我们…...

如何学好Python语言
学习Python:一场充满探索与实践的编程之旅 Python,作为一种解释型、交互式和面向对象的编程语言,近年来在数据科学、人工智能、Web开发等多个领域得到了广泛的应用。掌握Python,不仅可以提升个人的编程技能,还能够为未…...

计算机408网课评测+资料分享
408当然有比较好的网课推荐,比如王道的视频课 现在大部分人备战408基本都用王道的讲义,然后再搭配王道408的课程来听,可以学的很好。 其中408视频课中,我认为讲的比较好的是数据结构,和操作系统,计算机组…...

使用 ZipArchiveInputStream 读取压缩包内文件总数
读取压缩包内文件总数 简介 ZipArchiveInputStream 是 Apache Commons Compress 库中的一个类,用于读取 ZIP 格式的压缩文件。在处理 ZIP 文件时,编码格式是一个重要的问题,因为它决定了如何解释文件中的字符数据。通常情况下,Z…...

JavaScript对象修饰教程
在JavaScript中,对象修饰是一种常见的编程模式,用于动态地向对象添加新的功能或修改现有功能,同时保持对象的原始结构不变。对象修饰可以帮助我们实现代码的复用、扩展和维护,让代码更加灵活和可扩展。本文将深入探讨JavaScript对…...

转置卷积(transposed-conv)
一、什么是转置卷积 1、转置卷积的背景 通常,对图像进行多次卷积运算后,特征图的尺寸会不断缩小。而对于某些特定任务 (如图像分割和图像生成等),需将图像恢复到原尺寸再操作。这个将图像由小分辨率映射到大分辨率的尺寸恢复操作,…...

P1481 魔族密码
P1481 魔族密码 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 字典树 在插入字符串 s s s时,不断记录 s 0... k s_{0...k} s0...k的个数取最大即可。 #include <bits/stdc.h> using namespace std; const int N 1e5 21; int cnt[N], tr[N][30], idx,…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
