Pytorch 中的forward 函数内部原理
PyTorch中的forward函数是nn.Module类的一部分,它定义了模型的前向传播规则。当你创建一个继承自nn.Module的类时,你实际上是在定义网络的结构。forward函数是这个结构中最关键的部分,因为它指定了数据如何通过网络流动。
单独设计 forward 函数主要基于以下几点考虑:
1. 明确模型计算流程,构建网络结构:
通过定义forward函数,开发者可以清晰地指定模型在接收输入数据时如何执行计算。这包括层与层之间的连接方式、层内结构、激活函数的应用等。这种方式使得模型的结构变得非常直观,清晰,便于理解和修改。
2. 自动梯度计算:
Pytorch利用动态计算图(Dynamic Computation Graph)来自动计算梯度。当通过forward函数执行前向传播时,Pytorch会自动记录所有操作并构建计算图。在随后的反向传播过程中,这个计算图用于自动计算梯度。这意味着开发者只需关注forward函数中的计算逻辑,而无需手动编写梯度计算代码。
3. 模块化和重用:
通过将计算逻辑封装在forward函数中,Pytorch的nn.Module可以被轻松地复用和组合。这使得构建复杂模型变得简单,因为可以通过组合不同模块(每个模块都有自己的forward方法)来构建新的模型。
4. 灵活性:
Pytorch设计哲学是提供最大灵活性和控制力给开发者。通过编写自己的forward函数,开发者可以实现任何复杂模型或自定义模型的计算逻辑。这种设计既适用于标准神经网络结构,也适用于需要特殊处理的模型。
5. 与backward函数的分离:
在Pytorch中,backward函数是自动生成的。开发者只需定义forward函数,即可利用自动微分机制来计算梯度。这种设计简化了模型开发过程,使开发者能够专注于模型的前向传播定义。
总结来说,forward函数的设计体现了Pytorch核心设计理念,即保持了代码直观性和灵活性,同时实现了计算图构建和梯度计算的自动化,从而简化了深度学习模型设计和实现
自动调用和复用
- 自动调用:虽然自定义了
forward函数,但通常不会直接调用它。相反,当对模型实例进行调用并传递输入数据时,Pytorch自动调用forward函数。例如,模型实例是model,通常会这样做output = model(input),而不是直接调用output = model.forward(input)。这背后的魔法就是__call__方法,它在nn.Module中定义。当实例化一个模块时,__call__方法会被触发,它会在内部调用forward方法,并且还会处理一些其他重要的事务,比如钩子的执行。 - 钩子(Hooks):通过
__call__方法的自动调用机制,Pytorch提供了在执行forward函数之前和之后运行代码的能力。这对于调试、学习模型的内部工作原理、添加自定义逻辑等场景非常有用。 - 模块化和复用:通过定义forward函数,Pytorch让你能够以非常模块化的方式构建复杂的网络。可以定义小的、可重用的网络部分(如层、子网络等),并在forward函数中以灵活的方式将它们组合起来。这种设计提高了代码的可读性和复用性。
## 定义一个类
class model1:def __call__(self):print('call方法在模型实例化时被自动调用了')## 实例化
model1instance = model1()## 通过 __call__,自动调取类中的函数
model1instance()输出:
call方法在模型实例化时被自动调用了自动微分支持:在forward函数中执行的所有操作都被Pytorch的自动微分引擎所跟踪。这意味着,基于forward函数中定义的操作,Pytorch可以自动计算梯度,这对于训练过程中的反向传播是必需的。
forward 自动调用和自动微分支持:
import torch
import torch.nn as nn
class SimpleNet(nn.Module):def __init__(self):super(SimpleNet, self).__init__()self.fc1 = nn.Linear(10, 5) # 第一层:输入特征10个,输出特征5个self.relu = nn.ReLU() # 非线性激活函数ReLUself.fc2 = nn.Linear(5, 1) # 第二层:输入特征5个,输出特征1个def forward(self, x):x = self.fc1(x) # 数据通过第一层x = self.relu(x) # 应用ReLU激活函数x = self.fc2(x) # 数据通过第二层return x# 实例化模型
model = SimpleNet()# 创建一些随机数据作为输入
input = torch.randn(1, 10) # 假设我们有1个样本,每个样本有10个特征# 使用模型
output = model(input) # 注意,我们没有直接调用forward方法print()
print("模型输出是:")
print(output)
print()# 假设我们有一个目标值(标签),并计算损失
target = torch.tensor([[1.0]]) # 目标值
criterion = nn.MSELoss() # 使用均方误差作为损失函数
loss = criterion(output, target)# 反向传播计算梯度
loss.backward()# 查看第一层的权重梯度
print("第一层权重梯度如下:")
print(model.fc1.weight.grad)输出:
模型输出是:
tensor([[-0.0131]], grad_fn=<AddmmBackward>)第一层权重梯度如下:
tensor([[ 0.0000, -0.0000, -0.0000, 0.0000, -0.0000, -0.0000, -0.0000, 0.0000,0.0000, -0.0000],[ 0.5468, -0.5616, -0.4353, 0.4790, -1.2217, -0.6346, -0.2147, 0.3154,1.0077, -0.8762],[ 0.5550, -0.5700, -0.4419, 0.4862, -1.2402, -0.6442, -0.2180, 0.3202,1.0229, -0.8894],[ 0.0000, -0.0000, -0.0000, 0.0000, -0.0000, -0.0000, -0.0000, 0.0000,0.0000, -0.0000],[ 0.0000, -0.0000, -0.0000, 0.0000, -0.0000, -0.0000, -0.0000, 0.0000,0.0000, -0.0000]])
forward函数是定义Pytorch模型时的核心,它指定了数据的前向传播路径。虽然你定义了forward函数,但它是通过模型对象的调用间接触发的,这种设计既方便了模型的使用,也使得模型的设计更加灵活和强大。
相关文章:

Pytorch 中的forward 函数内部原理
PyTorch中的forward函数是nn.Module类的一部分,它定义了模型的前向传播规则。当你创建一个继承自nn.Module的类时,你实际上是在定义网络的结构。forward函数是这个结构中最关键的部分,因为它指定了数据如何通过网络流动。 单独设计 forward …...
四、C语言中的数组:如何输入与输出二维数组(数组,完)
本章的学习内容如下 四、C语言中的数组:数组的创建与初始化四、C语言中的数组:数组的输入与元素个数C语言—第6次作业—十道代码题掌握一维数组四、C语言中的数组:二维数组 1.二维数组的输入与输出 当我们输入一维数组时需要一个循环来遍历…...
基于python+vue智慧农业小程序flask-django-php-nodejs
传统智慧农业采取了人工的管理方法,但这种管理方法存在着许多弊端,比如效率低下、安全性低以及信息传输的不准确等,同时由于智慧农业中会形成众多的个人文档和信息系统数据,通过人工方法对知识科普、土壤信息、水质信息、购物商城…...

好用的GPTs:指定主题搜索、爬虫、数据清洗、数据分析自动化
好用的GPTs:指定主题搜索、爬虫、数据清洗、数据分析自动化 Scholar:搜索 YOLO小目标医学方面最新论文Scraper:爬虫自动化数据清洗数据分析 点击 Explore GPTs: Scholar:搜索 YOLO小目标医学方面最新论文 搜索 Scho…...

使用Qt自带windeployqt打包QML的exe
1.在开始菜单输入CMD找到对应的Qt开发版本,我的是Qt5.15.2(MinGW 8.1.0 64-bit)。 2.在控制台输入如下字符串,格式为 windeployqt exe绝对路径 --qmldir 工程的绝对路径 如下是我的打包代码。 我需要打包的exe的绝对路径 D:\Prj\Code\Demo\QML\Ana…...

C代码快速傅里叶变换-分类和推理-常微分和偏微分方程
要点 C代码例程函数计算实现: 线性代数方程解:全旋转高斯-乔丹消元,LU分解前向替换和后向替换,对角矩阵处理,任意矩阵奇异值分解,稀疏线性系统循环三对角系统解,将矩阵从完整存储模式转换为行索…...

计算机组成原理 双端口存储器原理实验
一、实验目的 1、了解双端口静态随机存储器IDT7132的工作特性及使用方法 2、了解半导体存储器怎样存储和读出数据 3、了解双端口存储器怎样并行读写,产生冲突的情况如何 二、实验任务 (1)按图7所示,将有关控制信号和和二进制开关对应接好,…...

[音视频学习笔记]六、自制音视频播放器Part1 -新版本ffmpeg,Qt +VS2022,都什么年代了还在写传统播放器?
前言 参考了雷神的自制播放器项目,100行代码实现最简单的基于FFMPEGSDL的视频播放器(SDL1.x) 不过老版本的代码参考意义不大了,我现在准备使用Qt VS2022 FFmpeg59重写这部分代码,具体的代码仓库如下: …...

GPT-5可能会在今年夏天作为对ChatGPT的“实质性改进”而到来
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
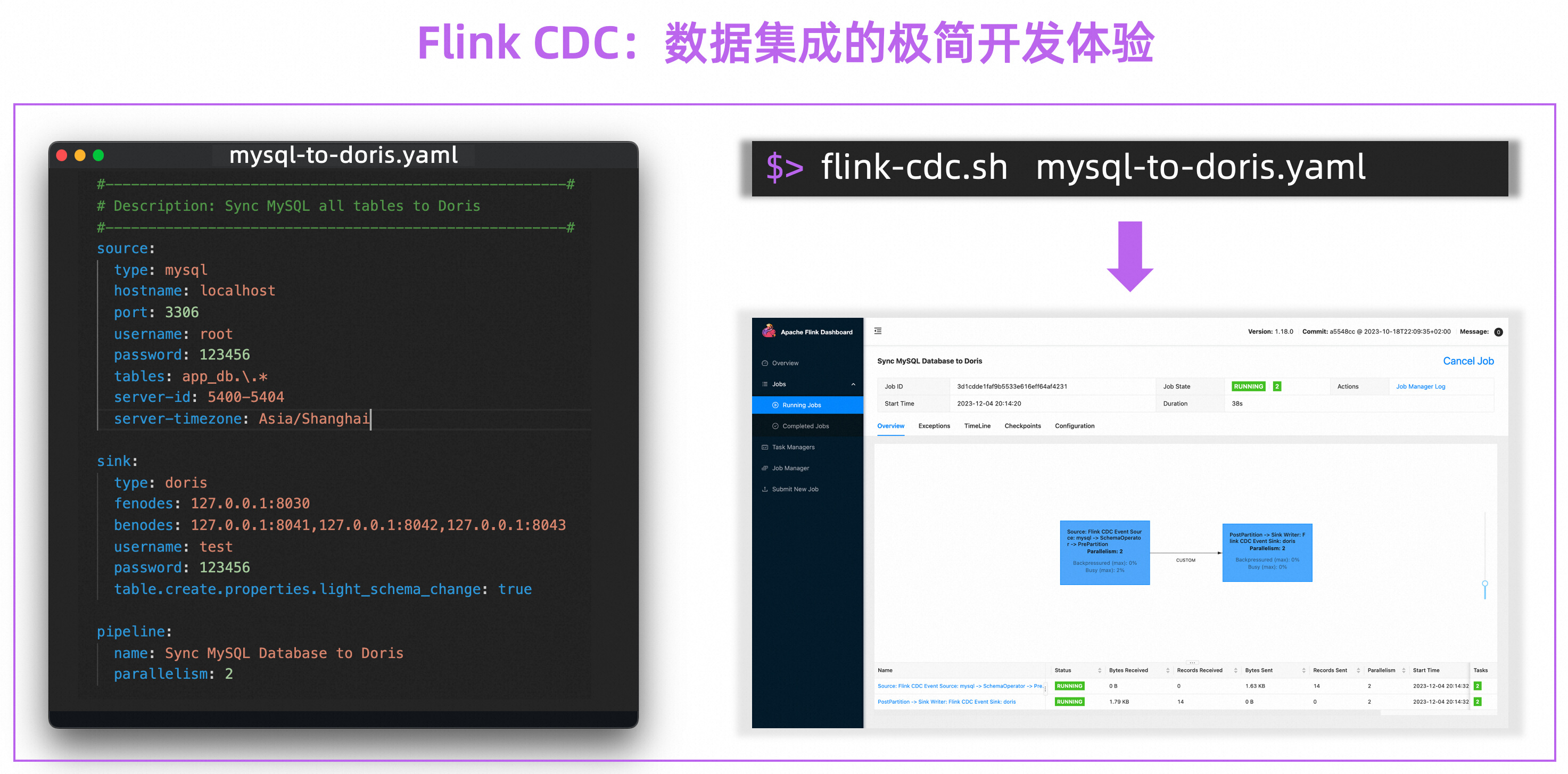
官宣|阿里巴巴捐赠的 Flink CDC 项目正式加入 Apache 基金会
摘要:本文整理自阿里云开源大数据平台徐榜江 (雪尽),关于阿里巴巴捐赠的 Flink CDC 项目正式加入 Apache 基金会,内容主要分为以下四部分: 1、Flink CDC 新仓库,新流程 2、Flink CDC 新定位,新玩法 3、Flin…...

部署单节点k8s并允许master节点调度pod
安装k8s 需要注意的是k8s1.24 已经弃用dockershim,现在使用docker需要cri-docker插件作为垫片,对接k8s的CRI。 硬件环境: 2c2g 主机环境: CentOS Linux release 7.9.2009 (Core) IP地址: 192.168.44.161 一、 主机配…...

Django日志(三)
内置TimedRotatingFileHandler 按时间自动切分的log文件,文件后缀 %Y-%m-%d_%H-%M-%S , 初始化参数: 注意 发送邮件的邮箱,开启SMTP服务 filename when=h 时间间隔类型,不区分大小写 S:秒 M:分钟 H:小时 D:天 W0-W6:星期几(0 = 星期一) midnight:如果atTime未指定,…...
【吾爱破解】Android初级题(二)的解题思路 _
拿到apk,我们模拟器打开看一下 好好,抽卡模拟器是吧😀 jadx反编译看一下源码 找到生成flag的地方,大概逻辑就是 java signatureArr getPackageManager().getPackageInfo(getPackageName(), 64).signaturesfor (int i 0; i &l…...

富格林:谨记可信计策安全做单
富格林悉知,现货黄金由于活跃的行情给投资者带来不少的盈利的机会,吸引着众多的投资者进场做单。但在黄金投资市场中一定要掌握可信的投资方法,提前布局好策略,这样才能增加安全获利的机会。不建议直接进入市场做单,因…...

【工具使用】mingw64编译完成运行可执行文件时出现乱码
一,问题现象: notepad设置的时UTF-8编码: mingw64命令行设置的编码格式为: 二,问题原因: 在执行的时候,windows下的编码格式是GBK 三,解决方法: 编译时࿰…...
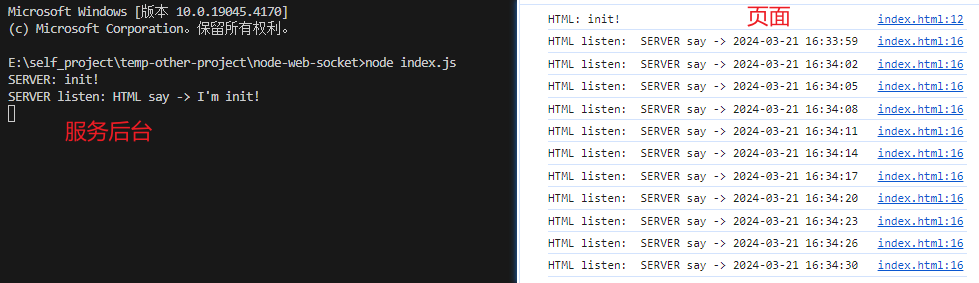
WebSocket 使用示例,后台为nodejs
效果图 页面代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>WebSocket Client</title&g…...

【算法】力扣【树形DP】687. 最长同值路径
【算法】力扣【树形DP】687. 最长同值路径 687. 最长同值路径 文章目录 【算法】力扣【树形DP】687. 最长同值路径题目描述输入输出示例 题解思路代码描述 复杂度分析总结 题目描述 本题要求在给定的二叉树中寻找最长的同值路径,这个路径中的每个节点的值都相同。…...
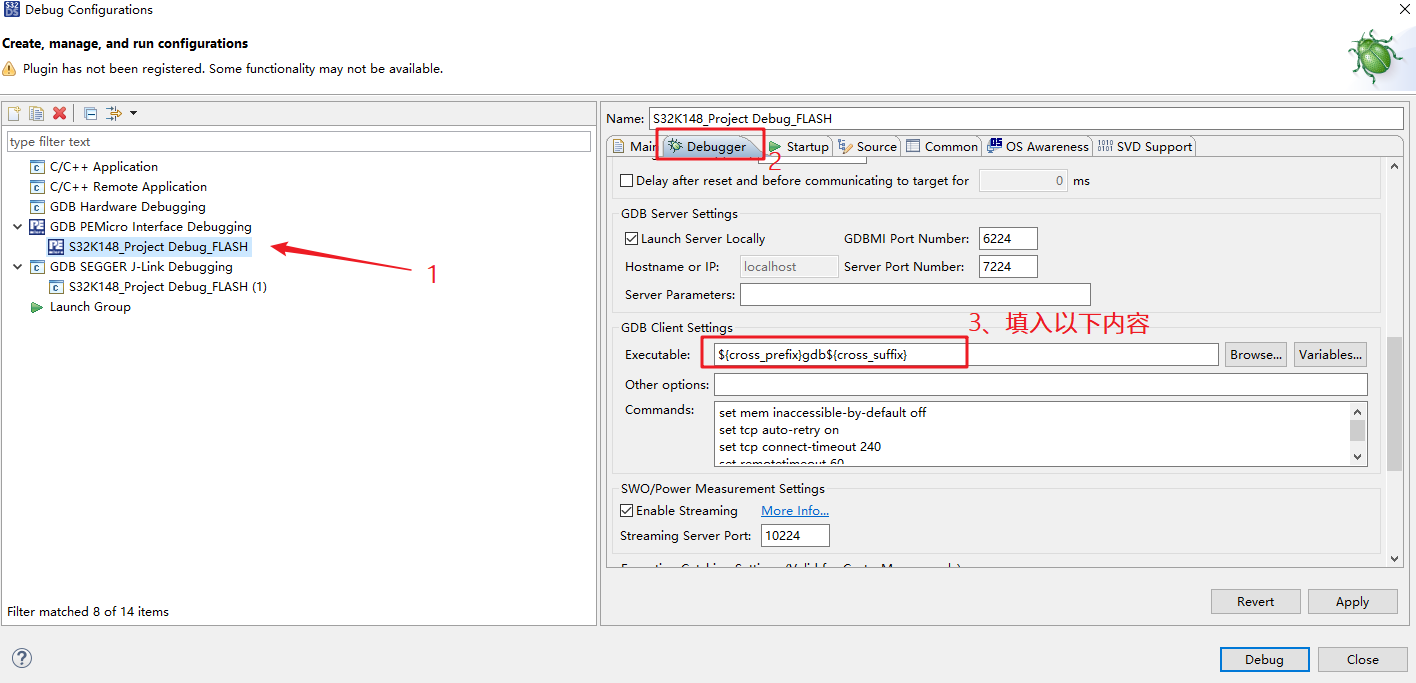
S32DS用PE调试报错
1、问题: 在S32DS上用PE进行调试报错: Error while launching command: --version 2、解决方法 按下图操作 填入内容: ${cross_prefix}gdb${cross_suffix}...
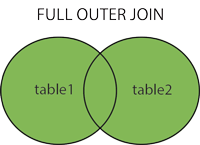
Day02-DDLDMLDQL(定义,操作,查询)(联合查询,子查询,字符集和校对集,MySQL5.7乱码问题)
文章目录 Day02-DDL&DML和DQL学习目标1. SQL语言的组成2. DDL2.1 数据库结构2.2 表结构2.3 约束2.3.1 主键约束(重要)(1)特点(2) 添加主键(3)删除主键(了解) 2.3.2 自增约束(1)特点(2) 添加自增约束(3)删除自增约束(了解) 2.3.3 非空约束(1)添加非空约束(2) 删除非空约束 2…...

3D高斯泼溅的崛起
沉浸式媒体领域正在以前所未有的速度发展,其中 3D 高斯溅射成为一项关键突破。 这项技术在广泛的应用中看起来非常有前景,并且可能会彻底改变我们未来创建数字环境以及与数字环境交互的方式。 在本文中,我们将通过与摄影测量和 NeRF 等前辈进…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
