【算法】力扣【树形DP】687. 最长同值路径
【算法】力扣【树形DP】687. 最长同值路径
687. 最长同值路径
文章目录
- 【算法】力扣【树形DP】687. 最长同值路径
- 题目描述
- 输入输出示例
- 题解思路
- 代码描述
- 复杂度分析
- 总结
题目描述
本题要求在给定的二叉树中寻找最长的同值路径,这个路径中的每个节点的值都相同。路径可以通过也可以不通过根节点,路径长度由节点间的边数表示。
其实就是在二叉树的直径的基础上,多考虑了每个节点的值而已。
输入输出示例
-
示例 1:
输入:root = [5,4,5,1,1,5]
输出:2解释: 最长的同值路径为树中的两个值为5的节点之间的路径,路径长度为2。
-
示例 2:
输入:root = [1,4,5,4,4,5]
输出:2解释: 最长的同值路径为树中值为4的两个相邻节点间的路径,或者值为5的两个相邻节点间的路径,路径长度均为2。
题解思路
为了解决这个问题,我们采用树形动态规划的方法。在处理任何一个节点时,我们需要知道以该节点为终点的最长同值路径,并且我们也需要知道经过该节点的最长同值路径长度。这两个信息可以帮助我们递归地求解整棵树。
代码描述
在代码中,我们定义一个递归函数dp,它返回两个值:
- 以当前节点为终点的最长同值路径长度。
- 当前节点的值。
代码中有四种情况需要考虑:
- 左子树和右子树的值与当前节点相同。
- 仅左子树的值与当前节点相同。
- 仅右子树的值与当前节点相同。
- 左右子树的值都与当前节点不同。
我们需要根据这些情况更新答案,并返回适当的值。以下是代码段及注释:
class Solution:def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:def dp(node):if node is None:return 0, -1cval = node.valleft, lval = dp(node.left)right, rval = dp(node.right)nonlocal ans# 情况1:左右子树的值均与当前节点相同if lval == rval == cval:ans = max(ans, left + right)return max(left, right) + 1, cval# 情况2:仅左子树的值与当前节点相同elif lval == cval:ans = max(ans, left)return left + 1, cval# 情况3:仅右子树的值与当前节点相同elif rval == cval:ans = max(ans, right)return right + 1, cval# 情况4:左右子树的值均与当前节点不同else:return 1, cvalans = 0dp(root)return ans
复杂度分析
- 时间复杂度: O ( n ) O(n) O(n),其中 n n n表示节点数量。每个节点仅被访问一次。
- 空间复杂度: O ( n ) O(n) O(n),其中 n n n表示节点的数量,因为在最坏的情况下树会退化成一条链。空间复杂度主要取决于递归时堆栈的深度。
总结
本题是一道中等难度的树形DP问题,通过分治的思想和递归实现,仅仅是在树形DP的外皮上套了一层需求,我们只需要思考一下如何将节点的值考虑进状态转移方程即可非常简单地解决这个问题。
相关文章:

【算法】力扣【树形DP】687. 最长同值路径
【算法】力扣【树形DP】687. 最长同值路径 687. 最长同值路径 文章目录 【算法】力扣【树形DP】687. 最长同值路径题目描述输入输出示例 题解思路代码描述 复杂度分析总结 题目描述 本题要求在给定的二叉树中寻找最长的同值路径,这个路径中的每个节点的值都相同。…...
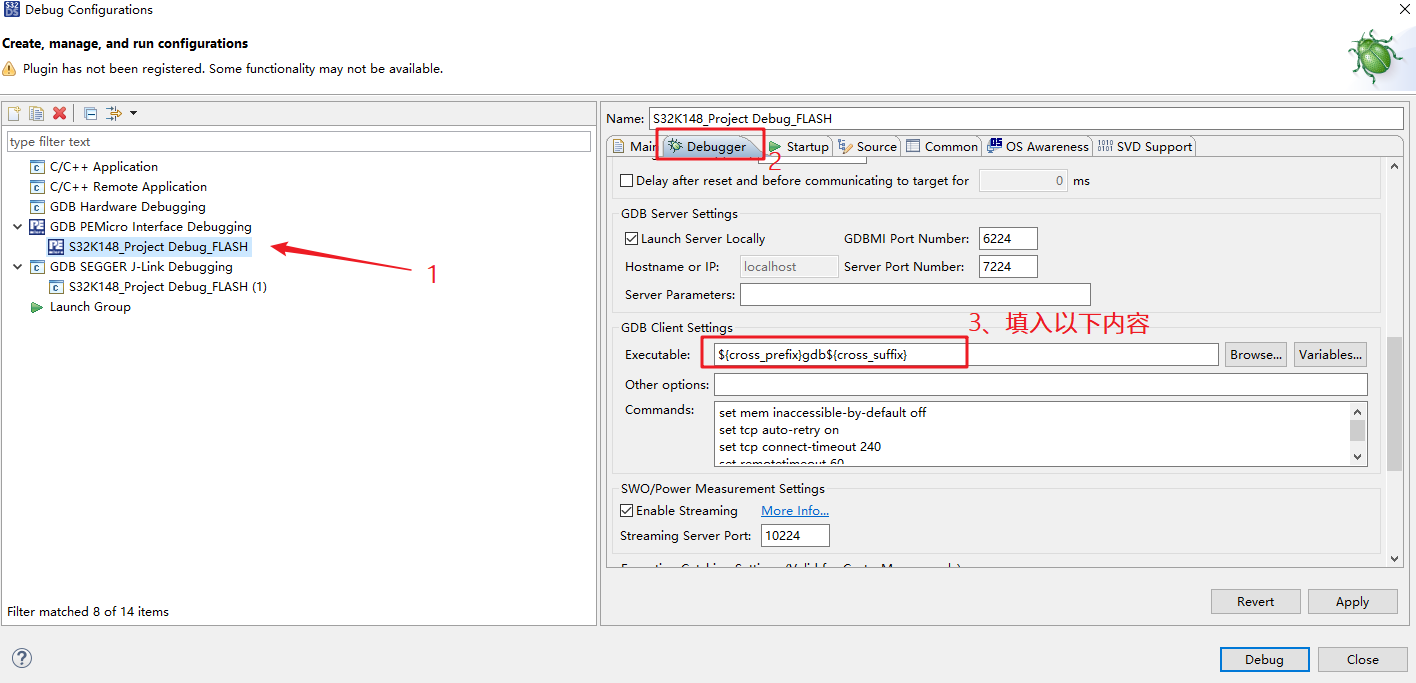
S32DS用PE调试报错
1、问题: 在S32DS上用PE进行调试报错: Error while launching command: --version 2、解决方法 按下图操作 填入内容: ${cross_prefix}gdb${cross_suffix}...
Day02-DDLDMLDQL(定义,操作,查询)(联合查询,子查询,字符集和校对集,MySQL5.7乱码问题)
文章目录 Day02-DDL&DML和DQL学习目标1. SQL语言的组成2. DDL2.1 数据库结构2.2 表结构2.3 约束2.3.1 主键约束(重要)(1)特点(2) 添加主键(3)删除主键(了解) 2.3.2 自增约束(1)特点(2) 添加自增约束(3)删除自增约束(了解) 2.3.3 非空约束(1)添加非空约束(2) 删除非空约束 2…...

3D高斯泼溅的崛起
沉浸式媒体领域正在以前所未有的速度发展,其中 3D 高斯溅射成为一项关键突破。 这项技术在广泛的应用中看起来非常有前景,并且可能会彻底改变我们未来创建数字环境以及与数字环境交互的方式。 在本文中,我们将通过与摄影测量和 NeRF 等前辈进…...
基于python+vue家政服务系统flask-django-php-nodejs
相比于以前的传统手工管理方式,智能化的管理方式可以大幅降低家政公司的运营人员成本,实现了家政服务的标准化、制度化、程序化的管理,有效地防止了家政服务的随意管理,提高了信息的处理速度和精确度,能够及时、准确地…...
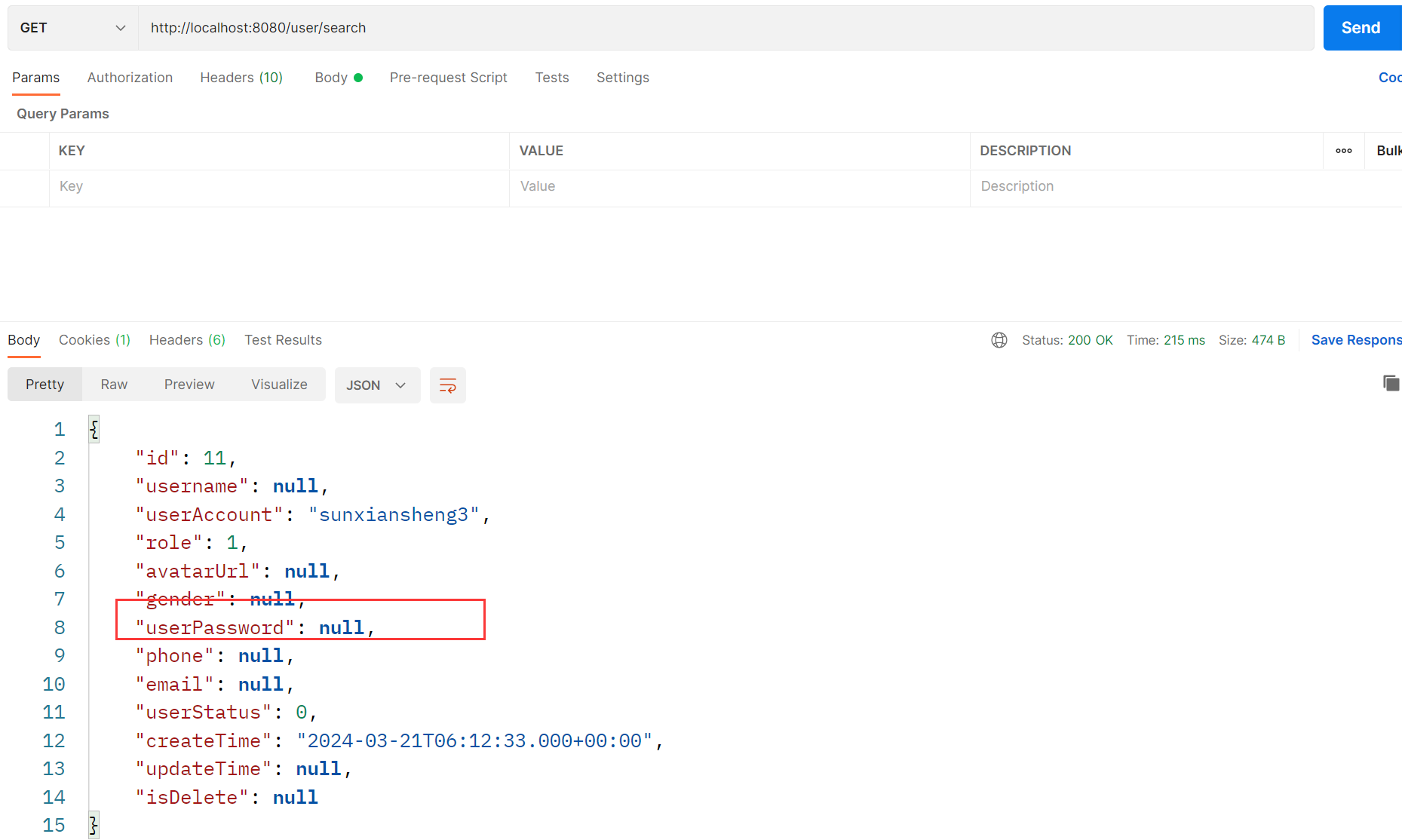
用户中心项目(登录 + 用户管理功能后端)
文章目录 1.登录功能-后端1.思路分析2.完成对用户名和密码的校验1.com/sun/usercenter/service/UserService.java 添加方法2.com/sun/usercenter/service/impl/UserServiceImpl.java 添加方法3.com/sun/usercenter/service/impl/UserServiceImpl.java 新增属性 3.记录用户的登录…...

嵌入式相机WEB,用C直接处理?
以前用HTTP连接相机的时候,以为是相机内部有一个类似tomcat之类的WEB服务器。收到相机命令后,通过链接库执行动作。 昨天想给相机增加一个时间显示,增加的项目一点就跳转到登录。 于是问了之前负责的,说是要后端改。再问嵌入式相…...

LeetCode_31_中等_下一个排列
文章目录 1. 题目2. 思路及代码实现详解(Python)2.1 两遍扫描 1. 题目 整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。 例如, a r r [ 1 , 2 , 3 ] arr [1,2,3] arr[1,2,3] ,以下这些都可以视作 a r r arr arr…...
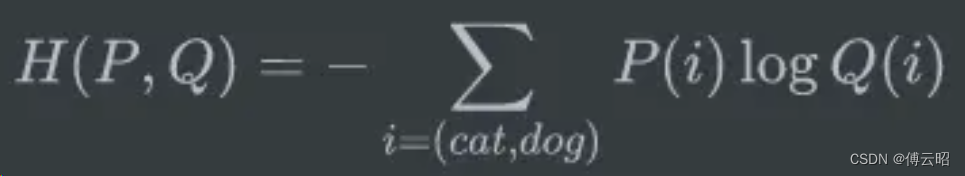
huggingface的transformers训练gpt
目录 1.原理 2.安装 3.运行 编辑 4.数据集 编辑 4.代码 4.1 model init编辑 forward: 总结: 关于loss和因果语言模型: 编辑 交叉熵:编辑 记录一下transformers库训练gpt的过程。 transformers/examples/…...

第六十一回 放冷箭燕青救主 劫法场石秀跳楼-编译安装飞桨paddlepaddle@openKylin+RISCV
卢俊义在水里被张顺抓住,用轿子抬到了梁山。宋江等人下马跪在地上迎接,请他坐第一把交椅。卢俊义宁死不从,大家只好说留他在山寨几天,先让李固带着马车货物回去。吴用对李固说,你的主人已经答应坐第二把交椅了…...

白话讲人工智能、机器学习、深度学习
人工智能(Artificial Intelligence,AI) 定义: 想象一个聪明的机器人,它能思考、决策和学习,就像电影里的智能角色那样。人工智能就是努力打造这样的智能实体的学科,它试图模仿、扩展乃至超越人…...
ssm项目(tomcat项目),定时任务(每天运行一次)相同时间多次重复运行job 的bug
目录标题 一、原因 一、原因 debug本地调试没有出现定时任务多次运行的bug,上传到服务器就出现多次运行的bug。(war的方式部署到tomcat) 一开始我以为是代码原因,或者是linux和win环境不同运行定时任务的方式不一样。 但是自己…...
vue3 + ts +element-plus + vue-router + scss + axios搭建项目
本地环境: node版本:20.10.0 目录 一、搭建环境 二、创建项目 三、修改页面 四、封装路由vue-router 五、element-plus 六、安装scss 七、封装axios 一、搭建环境 1、安装vue脚手架 npm i -g vue/cli 2、查看脚手架版本 vue -V3、切换路径到需…...

二叉树试题解析
一、单项选择题 01.下列关于二叉树的说法中,正确的是( C ). A.度为2的有序树就是二叉树 B.含有n个结点的二叉树的高度为 C.在完全二叉树中,若一个结点没有左孩子,则它必是叶结点 D.含有n个结点的完全二叉树的高度为解析:A 二叉树…...

计算机服务器中了faust勒索病毒怎么办,faust勒索病毒解密工具流程
网络是一把利剑,可以方便企业开展各项工作业务,为企业提供极大的便利,但随着网络技术的不断发展与应用,网络数据安全威胁也在不断增加,给企业的正常生产运营带来了极大困扰,近日,云天数据恢复中…...

初次部署麒麟V10系统需要的配置,快速完成测试环境的搭建
配置麒麟V10 设置“root”登录密码 sudo su -passwd # 设置登录密码允许“root”远程登录 sudo vim /etc/ssh/sshd_configsshd_config # ↓↓↓↓修改的内容↓↓↓↓ PermitRootLogin yes # ↑↑↑↑修改的内容↑↑↑↑重启服务 sudo systemctl restart sshd允许通过图像界…...

DOcker in Docker 原理与实战代码详解
Docker in Docker(DinD)指的是在Docker容器内部运行另一个Docker守护进程和客户端。这种技术可以用于创建嵌套的Docker环境,例如在持续集成/持续部署(CI/CD)管道中构建和测试Docker镜像。然而,需要注意的是…...

公司系统中了.rmallox勒索病毒如何恢复数据?
早晨上班时刻: 当阳光逐渐洒满大地,城市的喧嚣开始涌动,某公司的员工们纷纷踏入办公大楼,准备开始新的一天的工作。他们像往常一样打开电脑,准备接收邮件、查看日程、浏览项目进展。 病毒悄然发作: 就在员…...
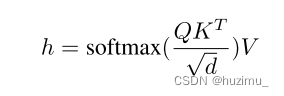
论文阅读:Forget-Me-Not: Learning to Forget in Text-to-Image Diffusion Models
Forget-Me-Not: Learning to Forget in Text-to-Image Diffusion Models 论文链接 代码链接 这篇文章提出了Forget-Me-Not (FMN),用来消除文生图扩散模型中的特定内容。FMN的流程图如下: 可以看到,FMN的损失函数是最小化要消除的概念对应的…...

html5cssjs代码 036 CSS默认值
html5&css&js代码 036 CSS默认值 一、代码二、解释 CSS默认值(也称为浏览器默认样式)是指当HTML元素没有应用任何外部CSS样式时,浏览器自动为这些元素赋予的一组基本样式。这些样式是由浏览器的默认样式表(User Agent sty…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
