C代码快速傅里叶变换-分类和推理-常微分和偏微分方程
要点
- C代码例程函数计算实现:
- 线性代数方程解:全旋转高斯-乔丹消元,LU分解前向替换和后向替换,对角矩阵处理,任意矩阵奇异值分解,稀疏线性系统循环三对角系统解,将矩阵从完整存储模式转换为行索引稀疏存储模式,稀疏系统的共轭梯度法,范德蒙矩阵,托普利茨矩阵,QR分解。
- 插值和外推:多项式,有理函数,三次样条,插值多项式的系数,双三次插值。
- 数值积分:龙伯格积分,第二个欧拉-麦克劳林求和,高斯求积和正交多项式,高斯-埃尔米特求积,高斯-雅可比求积,一元正交多项式。
- 评估函数:欧拉变换,加速序列收敛,连续分数的综合除法多项式,Ridders 多项式外推法,切比雪夫多项式,切比雪夫系数多项式近似,帕德近似值,有理切比雪夫近似。
- 特殊函数:对数伽马函数,指数积分,使用连续分数评估计算贝塔函数,整数阶贝塞尔函数,艾里函数,球面贝塞尔函数,球谐函数,菲涅尔积分,余弦和正弦积分,道森积分,椭圆积分和雅可比椭圆函数
- 随机数:最高质量随机数生成,高质量哈希值生成,滞后斐波那契生成器,生成指数偏差和逻辑偏差,Box-Muller 变换(正态偏差),柯西偏差,均匀比方法,伽玛偏差,泊松偏差,二项式偏差,多元正态偏差,蒙特卡洛积分应用,索博尔序列,VEGAS算法。
- 非线性方程集,最小最大函数,快速傅里叶变换,统计数据描述,数据模型,分类和推理,常微分方程积分,两点边界值问题,积分方程和反演理论,偏微分方程,计算几何,算法。
C/C++代码蒙特卡洛积分示例
对于光子学、经济学、视频游戏开发和工程学等许多依赖数值的领域来说,求解复杂积分是必需的。
I = ∫ a b g ( x ) d x I=\int_a^b g(x) d x I=∫abg(x)dx
许多有趣的问题都无法通过分析求解积分,因此必须应用替代数值方法来找到适当的估计。 值得注意的是,通过应用数值方法(例如蒙特卡洛积分),我们并不是“求解”积分,而是对积分值进行适当的估计。 对于许多应用来说,这种差异可以忽略不计,但应牢记这种区别,特别是在考虑当前问题所需的准确度时。
“蒙特卡洛方法”的现代变体可以追溯到 20 世纪 40 年代的洛斯阿拉莫斯实验室,该实验室最初开发该方法是为了帮助模拟核裂变过程,特别是模拟裂变材料中中子的平均自由程 。 我们没有确定地解决中子的扩散路径,而是应用了统计采样方法,而且效果非常好。 从那时起,“蒙特卡罗方法”一词根据其应用领域的不同而具有广泛的含义。 然而,蒙特卡罗的所有应用都有一个共同的基本原理,即使用统计采样来解决确定性难以解决的问题。
蒙特卡罗积分器
首先,我们可以使用蒙特卡罗检查积分的期望值。 传统上,函数 g(x) 的期望值可以通过首先乘以其概率密度函数 f(x),然后在所需区域上进行积分来计算:
E [ g ( x ) ] = ∫ a b g ( x ) f ( x ) d x E[g(x)]=\int_a^b g(x) f(x) d x E[g(x)]=∫abg(x)f(x)dx
或者,我们可以通过对积分极限之间的均匀分布重复采样来使用蒙特卡罗近似来获得期望值。
E [ g ( x ) ] = 1 n ∑ i = 1 n f ( x i ) E[g(x)]=\frac{1}{n} \sum_{i=1}^n f\left(x_i\right) E[g(x)]=n1i=1∑nf(xi)
其中, x i ∈ [ a , b ] x_i \in[a, b] xi∈[a,b]。
如前所述, x i x i xi 是从每个唯一 n = 1 , 2 , 3 n=1,2,3 n=1,2,3 等的限制 a a a 和 b b b 之间的均匀分布中采样的值。这种方法对 f ( x ) 进行采样 f(x) 进行采样 f(x)进行采样 函数并使用大数定律来找到收敛的期望值。
乘法因子 1 / n 1 / n 1/n 有时给出为 1 / ( n − 1 ) 1 /(n-1) 1/(n−1) 因为 n n n 个样本确实有 n − 1 n-1 n−1 个自由度,但是当 n n n 很大时 1 / n 1 / n 1/n 和 1 / ( n − 1 ) 1 /(n-1) 1/(n−1) 之间的差异可以忽略不计。给定期望值估计量的形式,扩展到积分的估计很简单。期望值公式乘以积分限制的范围,如下所示。
F = ( b − a ) 1 n ∑ i = 1 n f ( x i ) F=(b-a) \frac{1}{n} \sum_{i=1}^n f\left(x_i\right) F=(b−a)n1i=1∑nf(xi)
其中, x i ∈ [ a , b ] x_i \in[a, b] xi∈[a,b]。
积分估计使用期望值估计器以及由积分限制确定的矩形宽度来查找积分面积/体积的近似值。我们可以用一个相对简单的例子来测试它,取积分:
∫ 1 5 x 4 e − x d x \int_1^5 x^4 e^{-x} d x ∫15x4e−xdx
我们可以编写一个简短的 C++ 程序来应用蒙特卡罗积分技术,样本大小为 n = 200。
#include <iostream>
#include <cstdlib>
#include <cmath>double myFunction(double x);
double monteCarloEstimate(double lowBound, double upBound, int iterations);int main()
{double lowerBound, upperBound;int iterations;lowerBound = 1;upperBound = 5;iterations = 200;double estimate = monteCarloEstimate(lowerBound, upperBound,iterations);printf("Estimate for %.1f -> %.1f is %.2f, (%i iterations)\n",lowerBound, upperBound, estimate, iterations);return 0;
}double myFunction(double x)
//Function to integrate
{return pow(x,4)*exp(-x);
}double monteCarloEstimate(double lowBound, double upBound, int iterations)
{double totalSum = 0;double randNum, functionVal;int iter = 0;while (iter<iterations-1){randNum = lowBound + (float(rand())/RAND_MAX) * (upBound-lowBound);functionVal = myFunction(randNum);totalSum += functionVal;iter++;}double estimate = (upBound-lowBound)*totalSum/iterations;return estimate;
}它应该打印一些接近于:
Estimate for 1.0 -> 5.0 is 13.28, (200 iterations)
我们必须考虑蒙特卡罗积分技术隐含的方差。蒙特卡罗积分方案的方差遵循计算某个随机变量方差的传统过程。如果我们继续前面对函数 g ( x ) g(x) g(x) 求积分的表示法,则 g ( x ) g(x) g(x) 积分期望值的方差可以给出。为了简洁起见,我将跳过蒙特卡罗积分方案固有的标准差关系的推导。如果我们继续采用对函数 g ( x ) g(x) g(x) 进行积分的表示法,并且积分的期望值为 E [ g ( x ) ] E[g(x)] E[g(x)],则标准差的关系可以给出为:
σ n = V E [ g ( x ) 2 ] − E [ g ( x ) ] 2 n − 1 \sigma_n=V \sqrt{\frac{E\left[g(x)^2\right]-E[g(x)]^2}{n-1}} σn=Vn−1E[g(x)2]−E[g(x)]2
参阅一:计算思维
参阅二:亚图跨际
相关文章:

C代码快速傅里叶变换-分类和推理-常微分和偏微分方程
要点 C代码例程函数计算实现: 线性代数方程解:全旋转高斯-乔丹消元,LU分解前向替换和后向替换,对角矩阵处理,任意矩阵奇异值分解,稀疏线性系统循环三对角系统解,将矩阵从完整存储模式转换为行索…...

计算机组成原理 双端口存储器原理实验
一、实验目的 1、了解双端口静态随机存储器IDT7132的工作特性及使用方法 2、了解半导体存储器怎样存储和读出数据 3、了解双端口存储器怎样并行读写,产生冲突的情况如何 二、实验任务 (1)按图7所示,将有关控制信号和和二进制开关对应接好,…...

[音视频学习笔记]六、自制音视频播放器Part1 -新版本ffmpeg,Qt +VS2022,都什么年代了还在写传统播放器?
前言 参考了雷神的自制播放器项目,100行代码实现最简单的基于FFMPEGSDL的视频播放器(SDL1.x) 不过老版本的代码参考意义不大了,我现在准备使用Qt VS2022 FFmpeg59重写这部分代码,具体的代码仓库如下: …...

GPT-5可能会在今年夏天作为对ChatGPT的“实质性改进”而到来
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
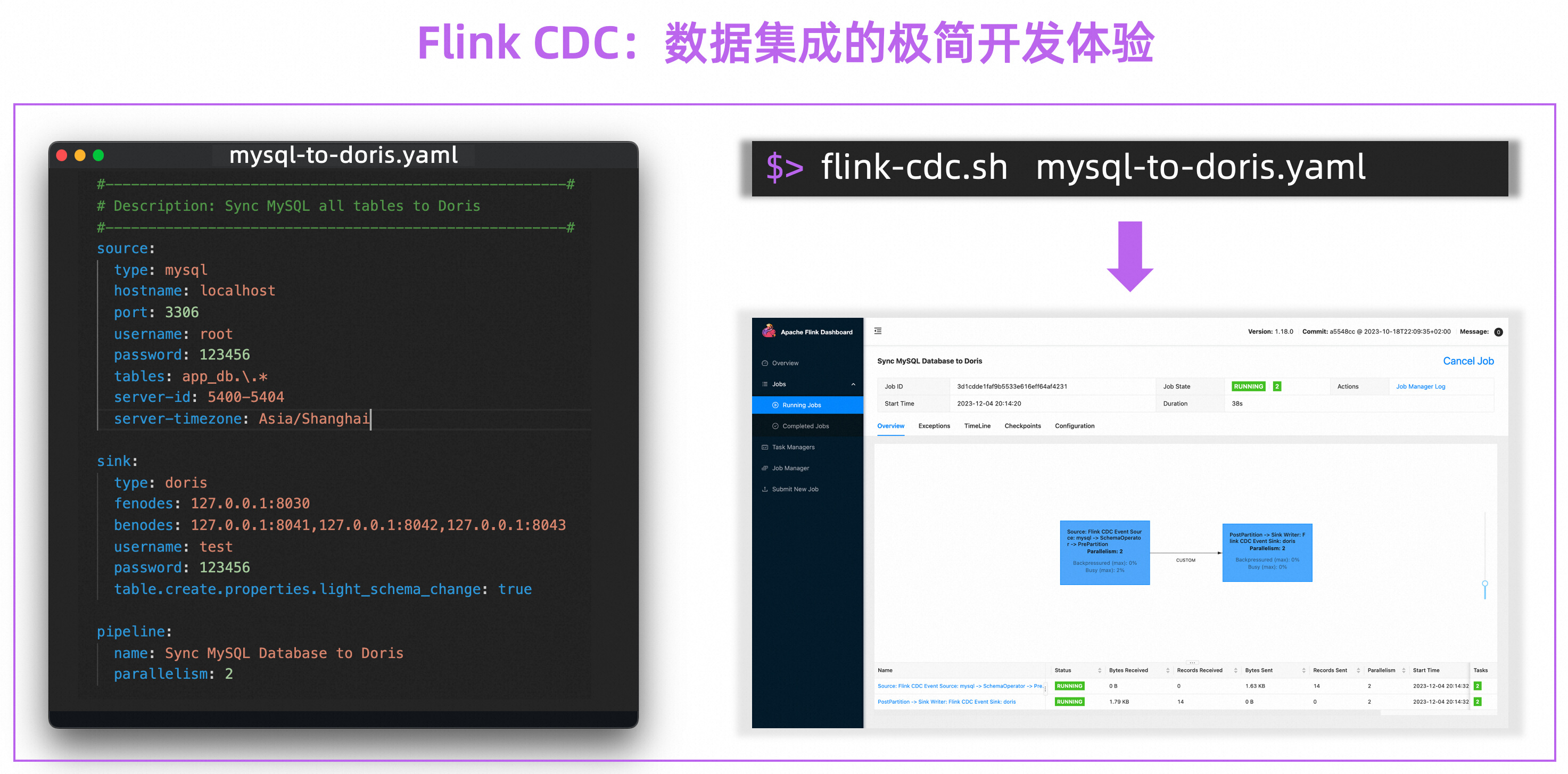
官宣|阿里巴巴捐赠的 Flink CDC 项目正式加入 Apache 基金会
摘要:本文整理自阿里云开源大数据平台徐榜江 (雪尽),关于阿里巴巴捐赠的 Flink CDC 项目正式加入 Apache 基金会,内容主要分为以下四部分: 1、Flink CDC 新仓库,新流程 2、Flink CDC 新定位,新玩法 3、Flin…...

部署单节点k8s并允许master节点调度pod
安装k8s 需要注意的是k8s1.24 已经弃用dockershim,现在使用docker需要cri-docker插件作为垫片,对接k8s的CRI。 硬件环境: 2c2g 主机环境: CentOS Linux release 7.9.2009 (Core) IP地址: 192.168.44.161 一、 主机配…...

Django日志(三)
内置TimedRotatingFileHandler 按时间自动切分的log文件,文件后缀 %Y-%m-%d_%H-%M-%S , 初始化参数: 注意 发送邮件的邮箱,开启SMTP服务 filename when=h 时间间隔类型,不区分大小写 S:秒 M:分钟 H:小时 D:天 W0-W6:星期几(0 = 星期一) midnight:如果atTime未指定,…...
【吾爱破解】Android初级题(二)的解题思路 _
拿到apk,我们模拟器打开看一下 好好,抽卡模拟器是吧😀 jadx反编译看一下源码 找到生成flag的地方,大概逻辑就是 java signatureArr getPackageManager().getPackageInfo(getPackageName(), 64).signaturesfor (int i 0; i &l…...

富格林:谨记可信计策安全做单
富格林悉知,现货黄金由于活跃的行情给投资者带来不少的盈利的机会,吸引着众多的投资者进场做单。但在黄金投资市场中一定要掌握可信的投资方法,提前布局好策略,这样才能增加安全获利的机会。不建议直接进入市场做单,因…...

【工具使用】mingw64编译完成运行可执行文件时出现乱码
一,问题现象: notepad设置的时UTF-8编码: mingw64命令行设置的编码格式为: 二,问题原因: 在执行的时候,windows下的编码格式是GBK 三,解决方法: 编译时࿰…...
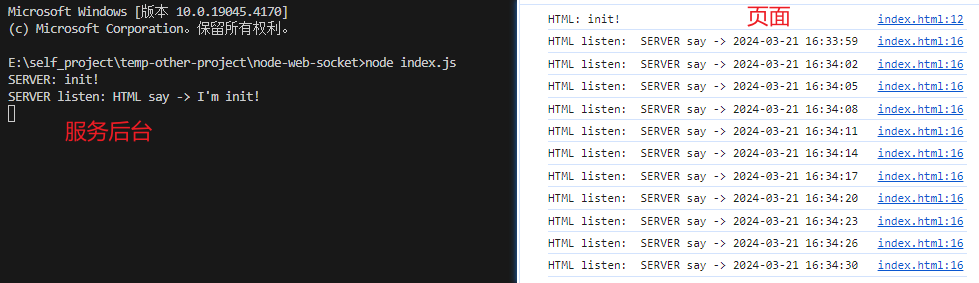
WebSocket 使用示例,后台为nodejs
效果图 页面代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>WebSocket Client</title&g…...

【算法】力扣【树形DP】687. 最长同值路径
【算法】力扣【树形DP】687. 最长同值路径 687. 最长同值路径 文章目录 【算法】力扣【树形DP】687. 最长同值路径题目描述输入输出示例 题解思路代码描述 复杂度分析总结 题目描述 本题要求在给定的二叉树中寻找最长的同值路径,这个路径中的每个节点的值都相同。…...
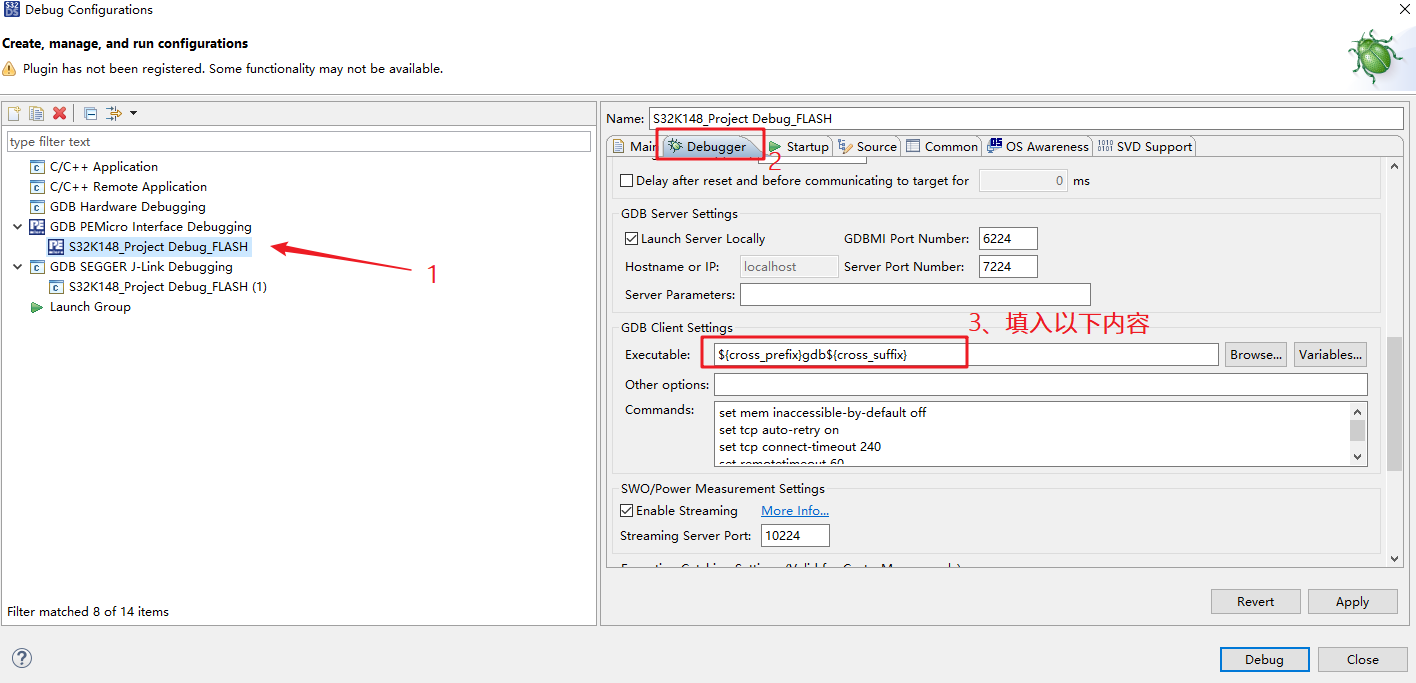
S32DS用PE调试报错
1、问题: 在S32DS上用PE进行调试报错: Error while launching command: --version 2、解决方法 按下图操作 填入内容: ${cross_prefix}gdb${cross_suffix}...
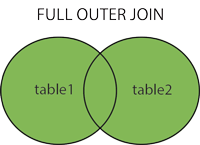
Day02-DDLDMLDQL(定义,操作,查询)(联合查询,子查询,字符集和校对集,MySQL5.7乱码问题)
文章目录 Day02-DDL&DML和DQL学习目标1. SQL语言的组成2. DDL2.1 数据库结构2.2 表结构2.3 约束2.3.1 主键约束(重要)(1)特点(2) 添加主键(3)删除主键(了解) 2.3.2 自增约束(1)特点(2) 添加自增约束(3)删除自增约束(了解) 2.3.3 非空约束(1)添加非空约束(2) 删除非空约束 2…...

3D高斯泼溅的崛起
沉浸式媒体领域正在以前所未有的速度发展,其中 3D 高斯溅射成为一项关键突破。 这项技术在广泛的应用中看起来非常有前景,并且可能会彻底改变我们未来创建数字环境以及与数字环境交互的方式。 在本文中,我们将通过与摄影测量和 NeRF 等前辈进…...
基于python+vue家政服务系统flask-django-php-nodejs
相比于以前的传统手工管理方式,智能化的管理方式可以大幅降低家政公司的运营人员成本,实现了家政服务的标准化、制度化、程序化的管理,有效地防止了家政服务的随意管理,提高了信息的处理速度和精确度,能够及时、准确地…...
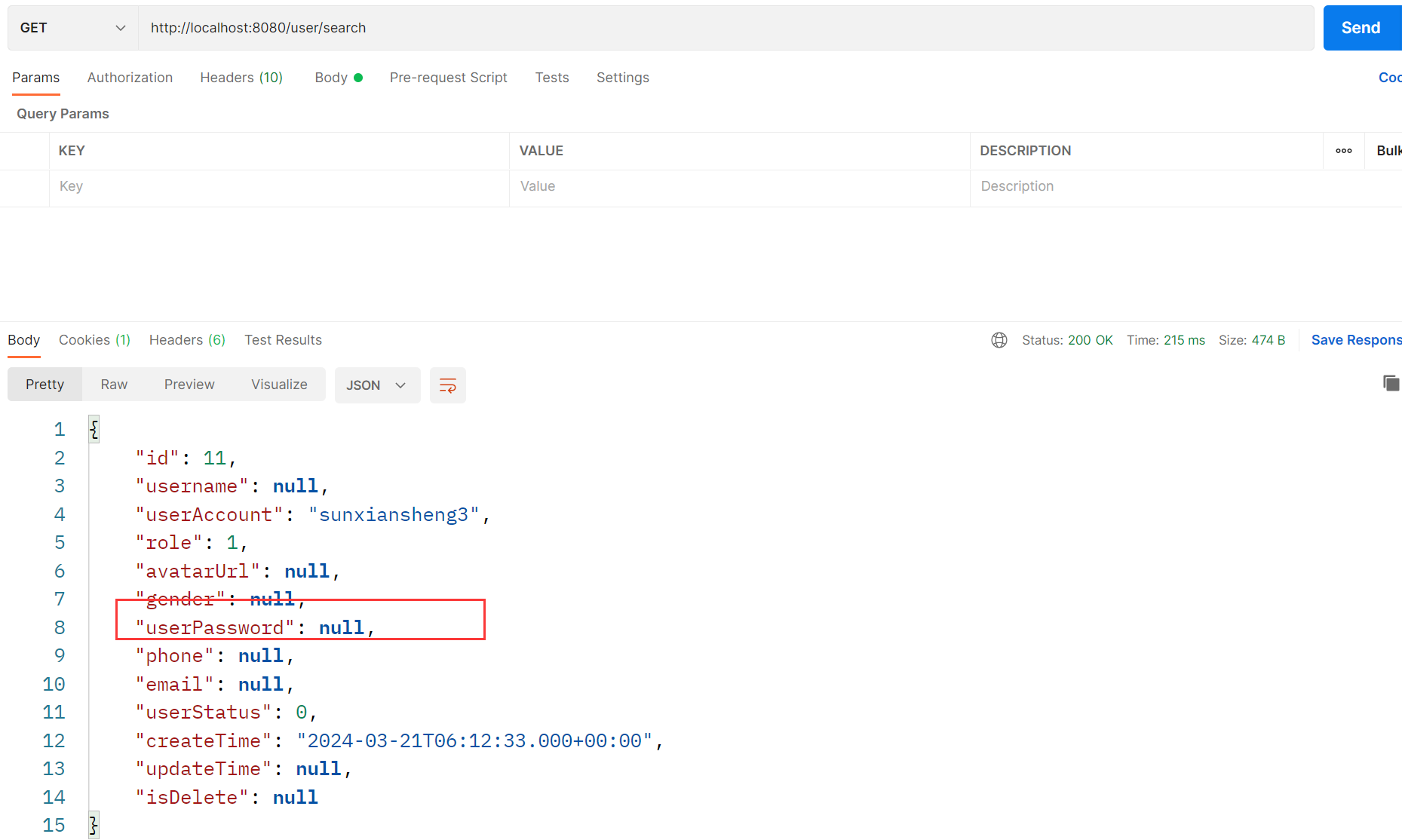
用户中心项目(登录 + 用户管理功能后端)
文章目录 1.登录功能-后端1.思路分析2.完成对用户名和密码的校验1.com/sun/usercenter/service/UserService.java 添加方法2.com/sun/usercenter/service/impl/UserServiceImpl.java 添加方法3.com/sun/usercenter/service/impl/UserServiceImpl.java 新增属性 3.记录用户的登录…...

嵌入式相机WEB,用C直接处理?
以前用HTTP连接相机的时候,以为是相机内部有一个类似tomcat之类的WEB服务器。收到相机命令后,通过链接库执行动作。 昨天想给相机增加一个时间显示,增加的项目一点就跳转到登录。 于是问了之前负责的,说是要后端改。再问嵌入式相…...

LeetCode_31_中等_下一个排列
文章目录 1. 题目2. 思路及代码实现详解(Python)2.1 两遍扫描 1. 题目 整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。 例如, a r r [ 1 , 2 , 3 ] arr [1,2,3] arr[1,2,3] ,以下这些都可以视作 a r r arr arr…...
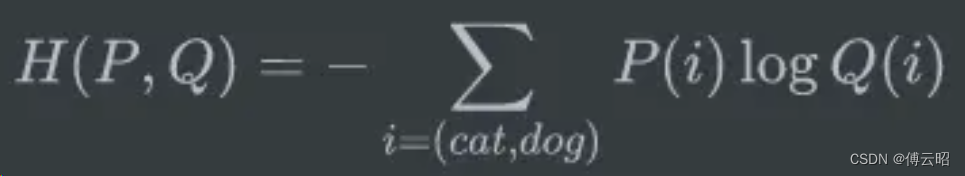
huggingface的transformers训练gpt
目录 1.原理 2.安装 3.运行 编辑 4.数据集 编辑 4.代码 4.1 model init编辑 forward: 总结: 关于loss和因果语言模型: 编辑 交叉熵:编辑 记录一下transformers库训练gpt的过程。 transformers/examples/…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
