【理解机器学习算法】之Clustering算法(K-Means)
实现 K-means 聚类从零开始涉及几个关键步骤:初始化质心、将点分配给最近的质心、根据分配更新质心,以及重复这个过程直到收敛。这里是一个基本的 Python 实现:
K-means 算法步骤:
- 初始化质心:从数据点中随机选择 `k` 个初始质心。
- 将点分配给最近的质心:对于数据集中的每个点,找到最近的质心并将该点分配到那个簇中。
- 更新质心:重新计算作为每个簇中所有点的平均值的质心。
- 重复:重复步骤 2 和 3,直到质心不再显著变化,表明算法已经收敛。
import numpy as npdef initialize_centroids(points, k):"""从数据点中随机初始化质心。"""indices = np.random.choice(points.shape[0], k, replace=False)return points[indices]def closest_centroid(points, centroids):"""返回一个数组,包含每个点到最近质心的索引。"""distances = np.sqrt(((points - centroids[:, np.newaxis])**2).sum(axis=2))return np.argmin(distances, axis=0)def update_centroids(points, closest, centroids):"""更新质心为每个簇分配的所有点的平均值。"""new_centroids = np.array([points[closest==k].mean(axis=0) for k in range(centroids.shape[0])])return new_centroidsdef k_means(points, k, max_iters=100):"""实现 K-means 算法。"""centroids = initialize_centroids(points, k)for _ in range(max_iters):closest = closest_centroid(points, centroids)new_centroids = update_centroids(points, closest, centroids)# 检查收敛if np.all(centroids == new_centroids):breakcentroids = new_centroidsreturn centroids, closest# 示例用法
if __name__ == "__main__":# 生成一些数据(例如,在 2D 空间中的两个簇)np.random.seed(42)cluster_1 = np.random.normal(0, 1, (100, 2))cluster_2 = np.random.normal(5, 1, (100, 2))points = np.vstack((cluster_1, cluster_2))# 应用 K-meansk = 2centroids, assignments = k_means(points, k)print("质心:\n", centroids)
K-means 算法的计算成本和时间成本主要依赖于几个因素:数据点的数量、特征的维数、质心的数量(k 值)以及算法迭代次数。算法的时间复杂度通常表示为 O(n*k*i*d),其中 n 是数据点的数量,k 是质心的数量,i 是迭代次数,d 是特征的维数。
计算成本和时间成本:
- 数据点数量(n):数据点越多,每次计算距离和更新质心的时间就越长。
- 质心数量(k):质心越多,计算每个数据点到每个质心的距离的成本就越高。
- 迭代次数(i):算法需要更多的迭代次数来收敛到最终的簇分配,特别是对于初始质心选择不理想或数据分布复杂的情况。
- 特征的维数(d):维度越高,计算距离就越复杂,因此时间成本更高。
局限性:
- 初始质心的选择:K-means 的结果可能对初始质心的选择非常敏感,不同的初始质心可能导致不同的最终簇划分。
- 簇的形状和大小:K-means 假设每个簇在所有方向上的方差都相同,因此它最适合识别球形簇。对于非球形簇或大小差异很大的簇,K-means 可能不会很有效。
- 确定 k 值:在实际应用中,确定最佳的 k 值(即簇的数量)通常是一个挑战。
- 局部最小值:K-means 可能会收敛到局部最优解而不是全局最优解,这意味着算法的结果可能不是最优的簇划分。
由于这些限制,虽然 K-means 在许多情况下都是一个有用和高效的聚类方法,但在应用时需要考虑数据的特性,并可能需要尝试不同的初始质心或使用如 K-means++ 这样的方法来改进初始质心的选择。
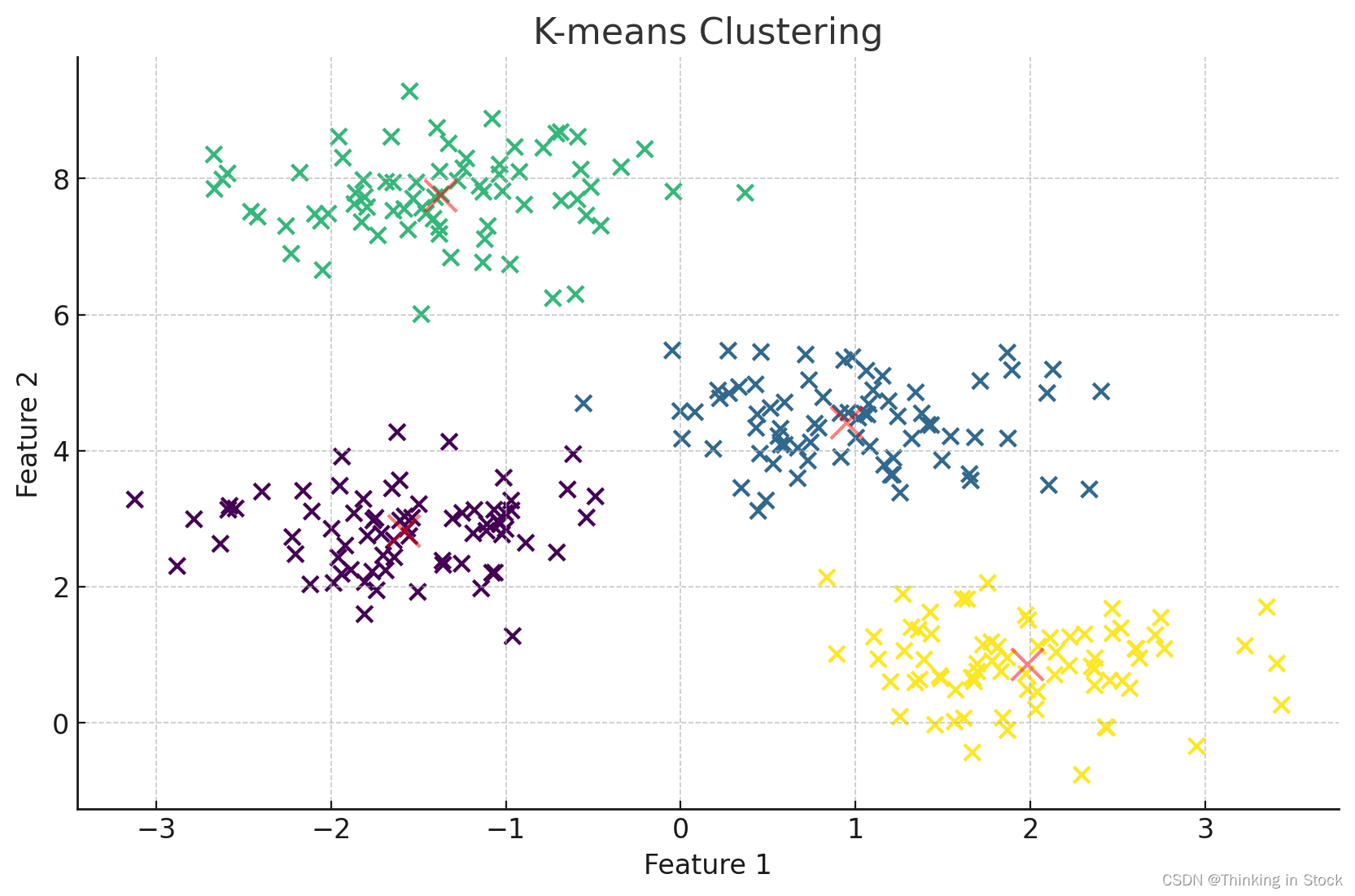
绘制二维的K-means
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans# Generate synthetic two-dimensional data
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)# Apply KMeans clustering
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)# Plot the data points
plt.scatter(X[:, 0], X[:, 1], s=50, c=y_kmeans, cmap='viridis')# Plot the centroids
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5)
plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
相关文章:

【理解机器学习算法】之Clustering算法(K-Means)
实现 K-means 聚类从零开始涉及几个关键步骤:初始化质心、将点分配给最近的质心、根据分配更新质心,以及重复这个过程直到收敛。这里是一个基本的 Python 实现: K-means 算法步骤: 初始化质心:从数据点中随机选择 k …...
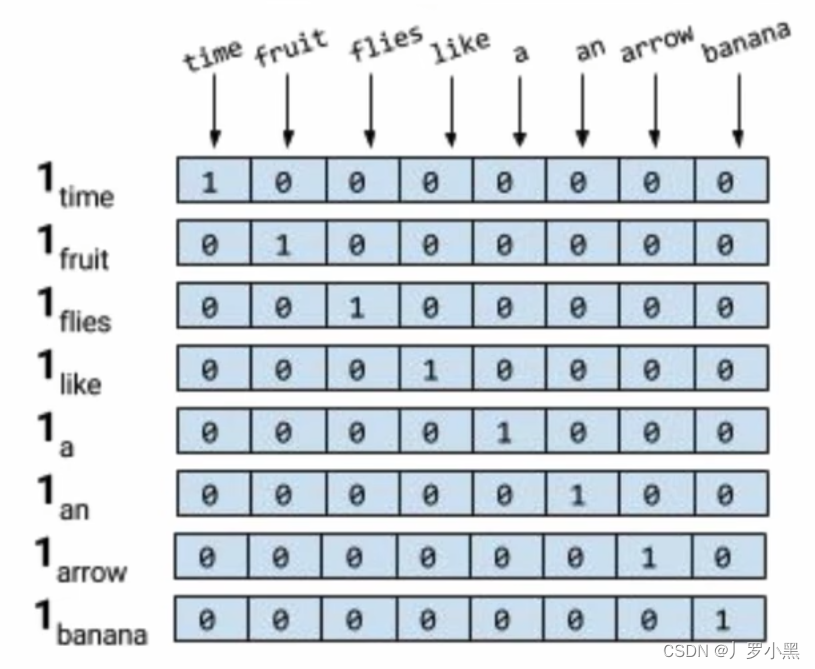
Transformer的前世今生 day02(神经网络语言模型、词向量)
神经网络语言模型 使用神经网络的方法,去完成语言模型的两个问题,下图为两层感知机的神经网络语言模型: 假设词典V内有五个词:“判断”、“这个”、“词”、“的”、“词性”,且要输出P(w_next | “判断”、“这个”、…...

【Linux】多线程编程基础
💻文章目录 📄前言🌺linux线程基础线程的概念线程的优缺点线程与进程的区别 线程的创建 🌻linux线程冲突概念互斥锁函数介绍加锁的缺点 📓总结 📄前言 无论你是否为程序员,相信多线程这个词汇应…...
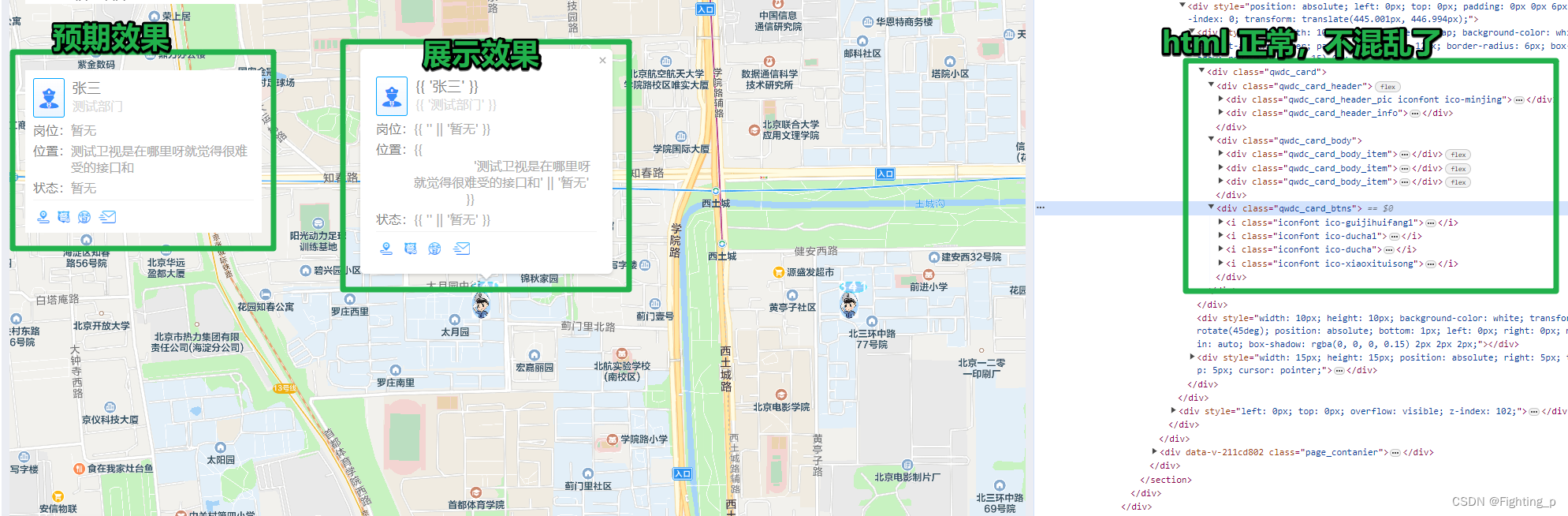
【地图】腾讯地图 - InfoWindow 自定义信息窗口内容时,内容 html 嵌套混乱问题
目录 需求描述问题问题代码页面展示 解决原因解决办法解决代码页面展示 代码汇总注 需求描述 腾讯地图上画点位,点击点位展示弹框信息 问题 问题代码 // 打开弹框 openInfoWindow(position, content) {this.infoWindow new TMap.InfoWindow({map: this.map,posit…...

Vue3、element-plus和Vue2、elementUI的一些转换
插槽 Vue3<template #default"scope"></template> <template #footer></template>Vue2<template slot-scope"scope"></template> <template slot"footer"></template>JS定义 Vue3 <script…...
Go语言gin框架中加载html/css/js等静态资源
Gin框架没有内置静态文件服务,但可以使用gin.Static或gin.StaticFS中间件来提供静态文件服务。 效果图如下: 一、gin 框架加载 Html 模板文件的方法 方式1:加载单个或多个html文件,需要指明具体文件名 r.LoadHTMLFiles("vie…...

#鸿蒙生态创新中心#揭幕仪式在深圳湾科技生态园举行
3 月 19 日,#鸿蒙生态创新中心#揭幕仪式在深圳湾科技生态园举行。 现场,深圳市南山区人民政府副区长李志娜发布《2024 年南山区支持鸿蒙原生应用发展首批政策措施清单》,从加强鸿蒙原生应用供给能力、推动鸿蒙原生应用产业集聚、完善鸿蒙原生…...

flask 继续学习
group_by group_by是一种在数据库查询或数据处理中常用的操作,它用于将数据按照指定的列进行分组。通过group_by操作,可以将数据集按照某个列的值进行分类,然后对每个分类进行聚合计算或其他操作。 在SQL语言中,group_by通常与聚…...

DockerFile遇到的坑
CMD 命令的坑 dockerfile 中的 CMD 命令在docker run -it 不会执行 CMD 命令。 FROM golang WORKDIR / COPY . ./All-in-one CMD ["/bin/sh","-c","touch /kkk.txt && ls -la"] RUN echo alias ll"ls -la" > ~/.bashrc(不…...
)
并网型风光储微电网日前优化调度(MATLAB实现)
考虑了光伏发电、风力发电、电池储能和负荷需求等因素,与主网相连不考虑向主网售电情况。 % 微电网日前优化调度示例代码% 定义时间步长(例如,每小时) time_steps 24;% 生成模拟数据:光伏发电量,风力发电…...
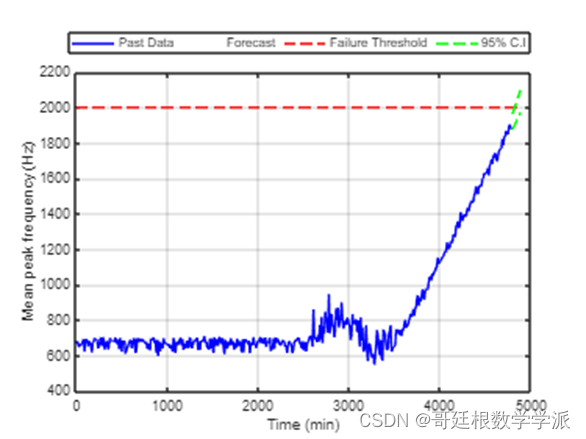
MATLAB环境下基于振动信号的轴承状态监测和故障诊断
故障预测与健康管理PHM分为故障预测和健康管理与维修两部分,PHM首先借助传感器采集关键零部件的运行状态数据,如振动信号、温度图像、电流电压信号、声音信号及油液分析等,提取设备的运行监测指标,进而实现对设备关键零部件运行状…...
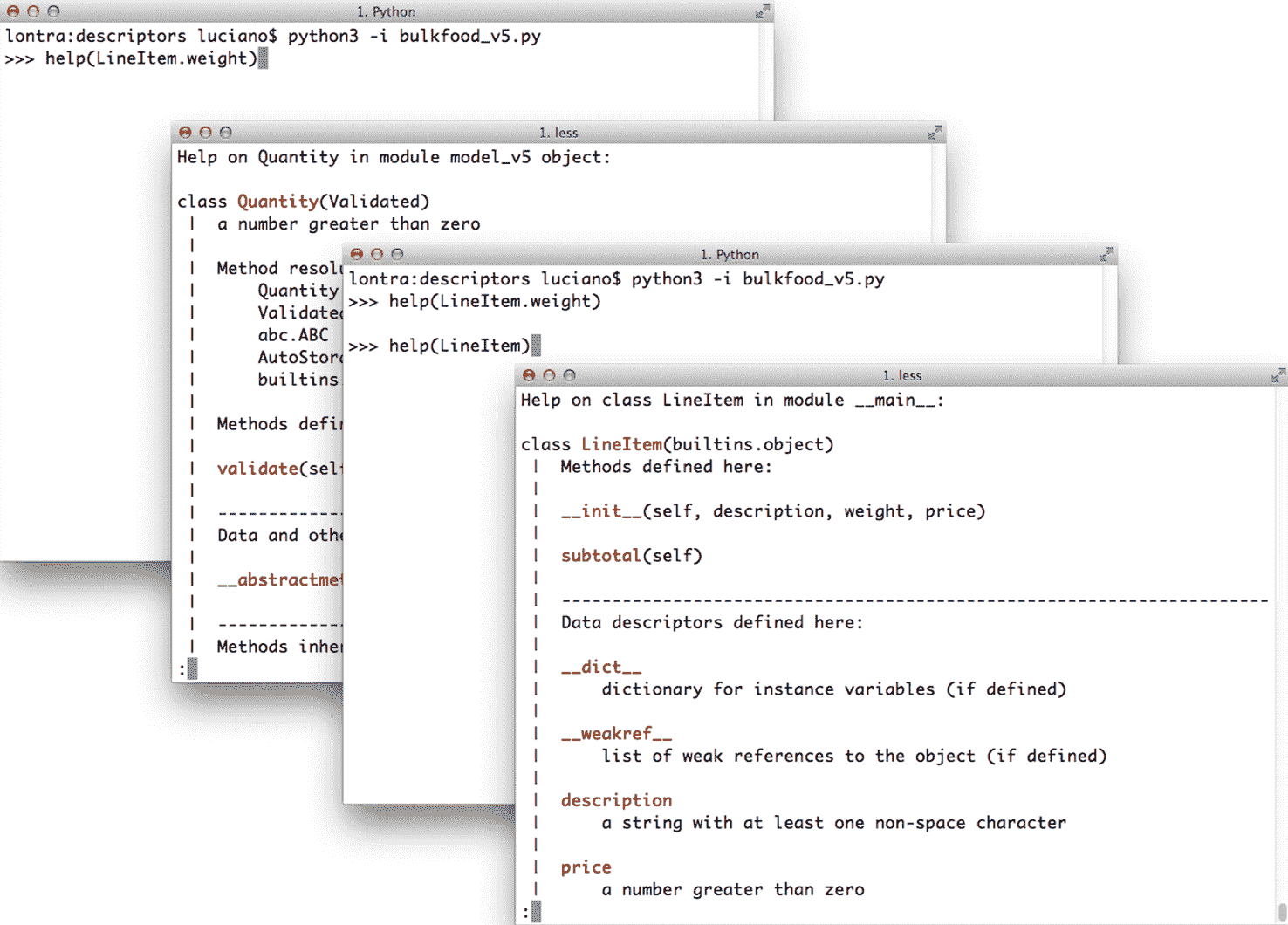
流畅的 Python 第二版(GPT 重译)(十二)
第五部分:元编程 第二十二章:动态属性和属性 属性的关键重要性在于,它们的存在使得将公共数据属性作为类的公共接口的一部分完全安全且确实可取。 Martelli、Ravenscroft 和 Holden,“为什么属性很重要” 在 Python 中࿰…...

【Python 48小时速成 2】关键字
文章目录 01. and :逻辑运算符,表示逻辑与操作。02. exec :内置函数,用于执行存储在字符串或文件中的 Python 代码。03. not :逻辑运算符,表示逻辑非操作。04. assert :断言语句,用于…...

小程序socket 全局代码
在微信小程序中,为了实现在整个应用范围内共享一个WebSocket连接,通常会将WebSocket的创建、打开、关闭以及消息收发等功能封装在一个全局模块中,然后在各个需要使用WebSocket功能的页面中引入并调用这个模块的方法。以下是一个简化的全局Web…...

数据挖掘|数据集成|基于Python的数据集成关键问题处理
数据挖掘|数据集成|基于Python的数据集成关键问题处理 1. 实体识别2. 数据冗余与相关性分析3. 去除重复记录4. 数据值冲突的检测与处理5. 基于Python的数据集成5.1 merge()方法5.2 Concat()方法 数据集成是把来自多个数据库或文件等不同数据源的数据整合成一致的数据存储。其中…...
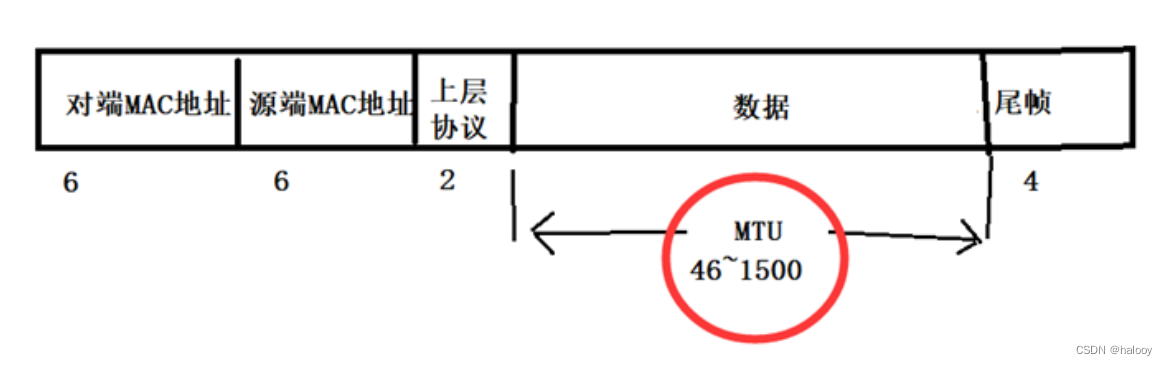
Linux-网络层IP协议、链路层以太网协议解析
目录 网络层:IP协议地址管理路由选择 链路层 网络层: 网络层:负责地址管理与路由选择 — IP协议,地址管理,路由选择 IP协议 数据格式: 4位协议版本:4-ipv4协议版本 4位首部长度:以…...

后端开发辅助
maven仓库手动添加jar命令 mvn install:install-file -DfileD:\\spire.xls-4.6.5.jar -DgroupIde-iceblue -DartifactIdspire.xls -Dversion4.6.5 -Dpackagingjaroracle调用存储过程示例 DECLAREPO_ERRCODE VARCHAR2(100);PO_ERRMSG VARCHAR2(100);BEGIN-- Call the procedure…...

插件电阻的工艺结构原理及选型参数总结
🏡《总目录》 目录 1,概述2,工作原理3,结构特点3.1,引脚设计3.2,电阻体3.3,封装4,工艺流程4.1,材料准备4.2,电阻体制作4.3,引脚焊接4.4,绝缘处理4.5,测试与筛选4.6,包装与存储...
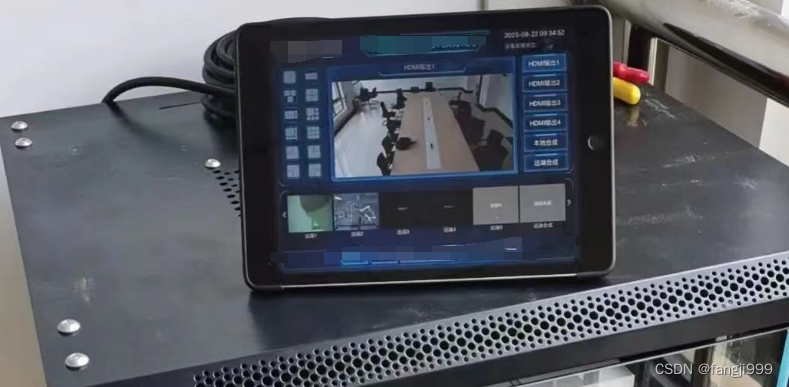
视频私有云,HDMI/AV多硬件设备终端接入,SFU/MCU视频会议交互方案。
在视频业务深入的过程中越来越多的硬件设备接入视频交互的视频会议中远程交互,有的是视频采集,有的是医疗影像等资料,都需要在终端承显,这就需要我们的设备终端能多设备,多协议接入,设备接入如下。 1&#…...

mac os 配置两个github账号
1. 清空git全局配置的username和email git config --global --unset user.name git config --global --unset user.emailgit config --list 可以查看是否清空了 2. 定义两个标识符,这两个标识符以后会被用来代替“github.com”来使用。 假设两个账号的邮箱地址分别是a@gmai…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
