深入理解与实践AB测试:从理论到实战案例解析
一、引言
在互联网产品优化和运营策略制定中,AB测试(也称为分组测试或随机化对照实验)是一种科学且严谨的方法。它通过将用户群体随机分配至不同的实验组(通常是A组和B组),对比不同版本的产品或策略对关键指标的影响,以此做出最优决策。本文将详细介绍AB测试的基本原理、实施步骤,并通过实际案例进行深度剖析。

二、AB测试基本原理
AB测试的核心在于“控制变量法”,即保持其他条件不变,仅改变一个因素(如产品设计、营销策略等),观察其对目标变量(如转化率、留存率等)的影响。例如,对于一款APP,我们可以为一部分用户展示新版的登录界面(B组),而另一部分用户则继续使用旧版界面(A组)。通过比较两组用户的登录转化率,可以判断新版界面是否优于旧版。
三、AB测试实施步骤
1. 定义问题和假设:首先明确要解决的问题或者要验证的假设,比如,“修改登录界面设计能否提高用户的登录转化率?”
2. 设定实验组与对照组:将用户随机分配至实验组(B组,接受新设计)和对照组(A组,维持原状)。
3. 选择关键指标:确定用于评估效果的关键性能指标(KPI),如点击率、转化率、留存率等。
4. 执行测试并收集数据:在一定时间内运行AB测试,确保样本量足够大以获得统计显著性。
5. 数据分析与解读结果:运用统计学方法对收集的数据进行分析,判断新方案是否优于原方案。
6. 决策与迭代:基于实证结果作出决策,如果新方案有效,则推广;无效则回滚或进一步优化。
四、AB测试实战案例
以某电商平台为例,该平台决定对商品详情页的设计进行优化,提出两个设计方案——A方案和B方案。通过AB测试,将用户流量均匀分为两部分,分别采用两种设计方案。
经过一段时间的测试后,发现B方案的商品详情页布局使得用户停留时间增长了15%,并且购物车添加率提高了10%。经统计检验,这些差异具有统计显著性。因此,平台方有足够的证据支持采用B方案的新设计。
五、AB测试中的统计学知识
AB测试的成功实施离不开统计学的支持。以下是几个关键的统计学概念和方法:
1. 样本大小与功效分析
在启动AB测试前,需要预先确定足够的样本大小,这可以通过功效分析来完成。功效分析主要考虑的因素包括预设的最小效应值(即新方案相比于原方案至少需要多大的改进才能被认为是有效的)、显著性水平α(一般取0.05,表示犯第一类错误的概率)、以及功效(即当真实存在效应时,检测出这个效应的概率,通常希望大于80%或90%)。
2. 假设检验
在AB测试中,我们通常采用双尾或单尾假设检验来确定实验结果是否显著。例如,零假设(H0)可能是“新旧方案的转化率无差异”,备择假设(H1)则是“新方案的转化率高于(或低于)旧方案”。通过计算p值,若p值小于预设的显著性水平α,则拒绝零假设,认为新方案在统计上显著优于旧方案。
3. 分布与置信区间
在衡量效果时,我们不仅关注点估计(如平均转化率),还要计算置信区间,了解估计的稳定性和精确度。例如,95%的置信区间意味着如果重复多次实验,95%的情况下真实的平均转化率会落入该区间内。
4. 多重比较与矫正
在进行多个AB测试时,如果没有进行适当的统计矫正,可能会增加犯第一类错误(假阳性)的概率。Bonferroni校正、Sidak校正、Holm-Bonferroni校正等方法可以帮助我们在面对多重比较问题时,保持整体的错误率在可接受范围内。
五、AB测试实例及代码分析
为了更直观地理解AB测试及其背后的统计学原理,我们将通过Python编程语言和一种常用的统计库——`statsmodels`来进行一个实际的AB测试分析示例。
假设一家电商网站对商品详情页面进行了优化(B版本),希望通过AB测试判断优化后的页面是否提升了用户的购买转化率。已有的原始数据如下:
import pandas as pd
import numpy as np
from statsmodels.stats.proportion import proportions_ztest
# 伪造AB测试数据
np.random.seed(123)
control_group = np.random.binomial(1, 0.1, size=1000) # 对照组(A组)1000个用户,转化率为10%
treatment_group = np.random.binomial(1, 0.15, size=1000) # 实验组(B组)1000个用户,转化率为15%
data = {
'group': ['A'] * 1000 + ['B'] * 1000,
'converted': control_group.tolist() + treatment_group.tolist()
}
df = pd.DataFrame(data)
print(df.head())
接下来,我们将利用`statsmodels`库进行假设检验,看B组的转化率是否显著高于A组:
# 计算各组转化人数和总人数
n_A = df[df['group'] == 'A']['converted'].sum()
N_A = df[df['group'] == 'A']['converted'].count()
n_B = df[df['group'] == 'B']['converted'].sum()
N_B = df[df['group'] == 'B']['converted'].count()
# 使用proportions_ztest进行假设检验
z_statistic, p_value = proportions_ztest([n_A, n_B], [N_A, N_B], alternative='larger')
# 输出结果
print("Z-统计量: ", z_statistic)
print("P值: ", p_value)
假设我们的显著性水平α设置为0.05,如果得到的P值小于0.05,那么我们就可以拒绝零假设,认为B组的转化率显著高于A组。
在上述代码中,`proportions_ztest`函数是基于二项分布的正态近似进行的假设检验,这里使用的“larger”参数代表我们是在做单尾检验,即只关心B组转化率是否更高。
七、总结
AB测试是一个涉及统计推断和决策的过程,要求我们在设计实验时,充分考虑统计学原理,合理确定样本大小,正确使用假设检验和置信区间,以及处理好多重比较问题。只有这样,我们才能从海量数据中提取出可靠的信息,科学地指导产品优化和业务决策。
AB测试是数据驱动决策的重要工具,能帮助我们避免主观臆断,用事实说话,精准提升产品性能和用户体验。但在实际应用中,还需要注意避免常见误区,如样本偏差、多重测试陷阱等问题,确保测试结果的有效性和可靠性。
以上只是AB测试的基础知识和实战应用初步介绍,深入实践还需结合具体业务场景灵活运用,持续优化,从而实现产品的精细化运营和持续增长。
相关文章:

深入理解与实践AB测试:从理论到实战案例解析
一、引言 在互联网产品优化和运营策略制定中,AB测试(也称为分组测试或随机化对照实验)是一种科学且严谨的方法。它通过将用户群体随机分配至不同的实验组(通常是A组和B组),对比不同版本的产品或策略对关键…...

flask之请求钩子
请求钩子是通过装饰器的形式实现,Flask支持如下四种请求钩子: 1、before_first_request: 在第一次请求处理之前先被执行 2、before_request: 在每次请求前执行 3、after_request: 在每次请求处理之后被执行 接受一个参数:视图函数的响应在…...

COPY requires at least two arguments, docker COPY 报错
COPY requires at least two arguments # 使用 Node.js 12.16.0FROM node:12.16.0WORKDIR /appCOPY ..原因:Dockerfile文件COPY后的两个. 要加空格 本内容来源于小豆包,想要更多内容请跳转小豆包 》...

权限提升-Web权限提升篇划分获取资产服务后台系统数据库管理相互转移
知识点 1、权限提升转移-分类&高低&场景 2、Web权限提升及转移-后台&数据库 3、后台权限及转移-转移对象&后台分类 章节点: 1、Web权限提升及转移 2、系统权限提升及转移 3、宿主权限提升及转移 4、域控权限提升及转移 基础点 0、为什么我们要学…...

【Unity每日一记】unity中的内置宏和条件编译(Unity内置脚本符号)
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:uni…...

发现有一个会Python的男友魅力值杠杠的!!!
Python能做什么? 可以做日常任务,比如自动备份你的MP3,可以做网站,很多著名的网站像知乎、YouTube就是Python写的, 可以做网络游戏的后台,很多在线游戏的后台都是Python开发的。 上面说的这些本人并没有实…...

SQL日期函数
文章目录 1.获取日期时间函数1.1 获取当前日期时间1.2 获取当前日期1.3 获取当前时间 2.日期格式化★★★2.1 日期转指定格式字符串2.2 字符串转日期 3.日期间隔3.1 增加日期间隔 ★★★3.2 减去一个时间间隔★★★3.3 日期相差天数(天)3.4 相差时间&…...
)
C语言经典面试题目(二十六)
1、解释一下C语言中的函数原型及其作用。 函数原型是指在函数定义之前声明函数的参数类型、返回类型和函数名称的一种声明方式。函数原型的作用包括: 编译器检查:函数原型能够告诉编译器函数的返回类型和参数类型,从而能够在编译阶段检查函…...

创建一个electron-vite项目
前置条件:非常重要!!! npm: npm create quick-start/electronlatest yarn: yarn create quick-start/electron 然后进入目录,下载包文件,运行项目 到以上步骤,你已经成功运行起来一个 electr…...

Codeforces Round 935 (Div. 3)A~E
A. Setting up Camp 题目分析: 有三种人,内向、外向、综合,内向必须独自一个帐篷,外向必须3个人一个帐篷,综合介于1~3人一个帐篷,我们发现非法情况只会存在外向的人凑不成3个人一个帐篷的情况,因外向不够可…...

ES: spring boot中使用ElasticsearchClient
一、依赖:(要根据不同版本的ES来调整依赖,否则会报错,不支持太低版本的ES,比如7.6以下的) <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-e…...

实体框架EF(Entity Framework)简介
实体框架EF(Entity Framework)简介 文章目录 实体框架EF(Entity Framework)简介一、概述二、O/R Mapping是什么采用O/R Mapping带来哪些好处 三、Entity Framework架构3.1 下图展示了Entity Framework的整体架构3.2 Entity Framew…...

使用CUDA 为Tegra构建OpenCV
返回:OpenCV系列文章目录(持续更新中......) 上一篇:MultiArch与Ubuntu/Debian 的交叉编译 下一篇:在iOS中安装 警告: 本教程可能包含过时的信息。 使用CUDA for Tegra 的OpenCV 本文档是构建支持 CUD…...
YoloV8改进策略:BackBone改进|PKINet
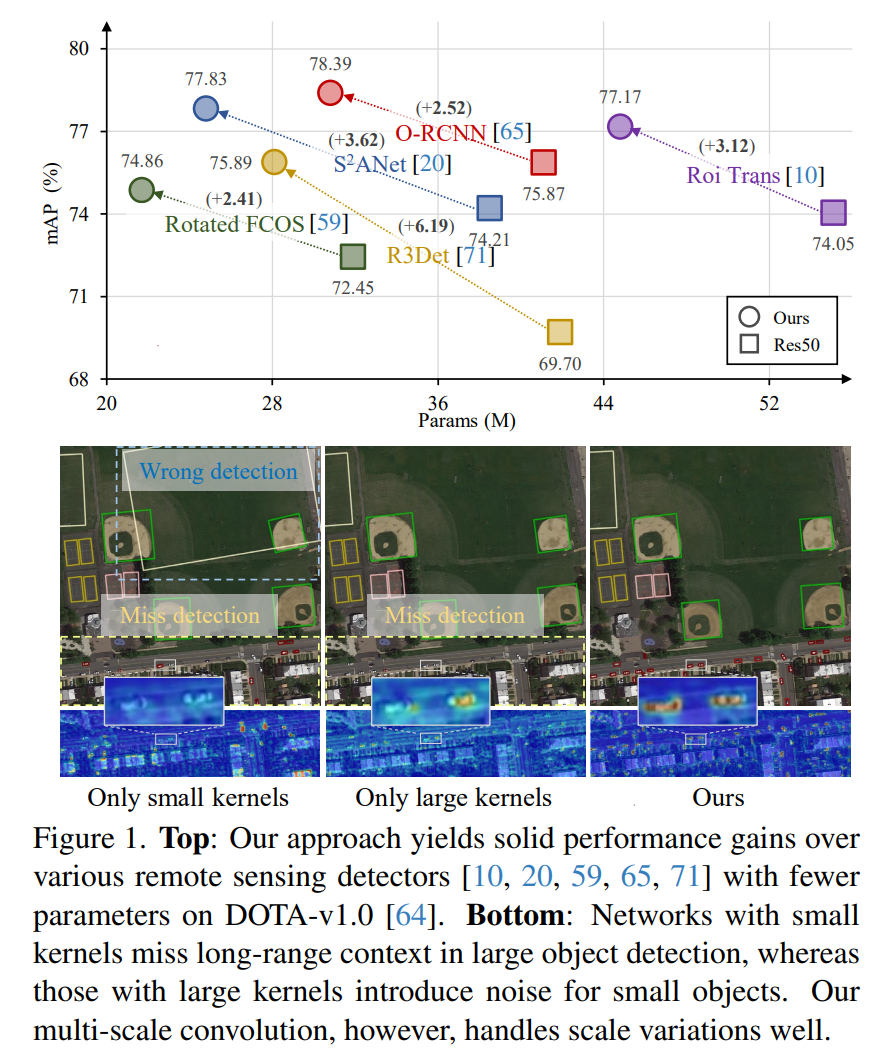
摘要 PKINet是面向遥感旋转框的主干,网络包含了CAA、PKI等模块,给我们改进卷积结构的模型带来了很多启发。本文,使用PKINet替代YoloV8的主干网络,实现涨点。PKINet是我在作者的模型基础上,重新修改了底层的模块,方便大家轻松移植到YoloV8上。 论文:《Poly Kernel Ince…...
如何在Linux系统部署Dupal CMS结合内网穿透实现无公网IP访问web界面
文章目录 前言1. Docker安装Drupal2. 本地局域网访问3 . Linux 安装cpolar4. 配置Drupal公网访问地址5. 公网远程访问Drupal6. 固定Drupal 公网地址 正文开始前给大家推荐个网站,前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默&a…...

小巧玲珑的SQLite
SQLite是桌面端和移动端的不错选择 前言 SQLite身影无处不在。 SQLite,是一款轻型的数据库,是遵守ACID的关系型数据库管理系统,它的设计目标是嵌入式的,而且目前已经在很多嵌入式产品中使用了它,它占用资源非常的低&a…...

【Android 内存优化】 native内存泄漏监控方案源码分析
文章目录 前言使用效果使用apiJNI的动态注册native方法动态注册 hook的实现android_dlopen_ext和dl_iterate_phdr naive监控的实现nativeGetLeakAllocs 总结 前言 Android的native泄漏怎么检测?下面通过研究开源项目KOOM来一探究竟。 使用效果 未触发泄漏前的日志…...
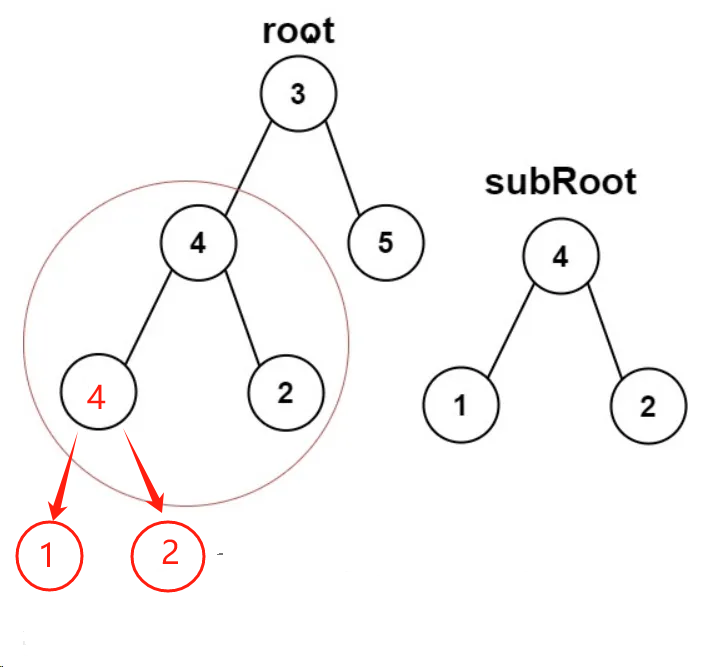
数据结构 二叉树 力扣例题AC——代码以及思路记录
LCR 175. 计算二叉树的深 某公司架构以二叉树形式记录,请返回该公司的层级数。 AC int calculateDepth(struct TreeNode* root) {if (root NULL){return 0;}else{return 1 fmax(calculateDepth(root->left), calculateDepth(root->right));} } 代码思路 …...

Android 11系统启动流程
在Android 11系统启动流程中,系统启动主要经历了以下几个阶段: 引导加载程序(Bootloader)启动: 当设备加电后,首先运行的是ROM Bootloader,它负责验证操作系统映像的完整性、初始化基本硬件并加…...
python 爬取杭州小区挂牌均价
下载chrome驱动 通过chrome浏览器的 设置-帮助-关于Google Chrome 查看你所使用的Chrome版本 驱动可以从这两个地方找: 【推荐】https://storage.googleapis.com/chrome-for-testing-publichttp://npm.taobao.org/mirrors/chromedriver import zipfile import os import r…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...
