Codeforces Round 935 (Div. 3)A~E
A. Setting up Camp

题目分析:
有三种人,内向、外向、综合,内向必须独自一个帐篷,外向必须3个人一个帐篷,综合介于1~3人一个帐篷,我们发现非法情况只会存在外向的人凑不成3个人一个帐篷的情况,因外向不够可以向综合人借,故将二者合并并判断:
#include<bits/stdc++.h>
#pragma GCC optimize("Ofast")
#define INF 1e18
#define IOS ios::sync_with_stdio(false);cin.tie(0);
#define int long long
#define pb push_back
#define vct vector
#define checkbit __builtin_popcount
#define gcd __gcd
#define use int T;cin>>T;while(T--)
#define LEN length()
#define all(a) a.begin()+1,a.end()
template<class T> bool mmax(T &u, T v) { return u < v ? (u = v, 1) : 0; }
template<class T> bool mmin(T &u, T v) { return u > v ? (u = v, 1) : 0; }
#define lowbit(x) (x&(-x))
#define yes cout<<"YES"<<'\n'
#define no cout<<"NO"<<'\n'
#define safe_map unordered_map<int, int, custom_hash>
using namespace std;
typedef pair<int,int>pii;
const int N =2e5+7;
struct custom_hash {
size_t operator()(uint64_t x) const {
static const uint64_t FIXED_RANDOM = chrono::steady_clock::now().time_since_epoch().count();
x ^= FIXED_RANDOM;
return x ^ (x >> 16);
}
};
signed main()
{IOSuse{int a,b,c;cin>>a>>b>>c;int x=b%3;if(x+c<3&&x!=0)cout<<"-1"<<endl;// 非法情况else cout<<a+(b+c)/3+((b+c)%3?1:0)<<endl;//else}
return 0;
}B. Fireworks

题目分析:
A类烟花每a分钟发射一次,B类烟花每b分钟发射一次,它们都能持续m分钟,那么我们直接用m分别求出这两类烟花都能放几个加和即可,注意, 我们可以选择烟花发射时间包含二者最小公倍数所以最终结果+2
#include<bits/stdc++.h>
#pragma GCC optimize("Ofast")
#define INF 1e18
#define IOS ios::sync_with_stdio(false);cin.tie(0);
#define int long long
#define pb push_back
#define vct vector
#define checkbit __builtin_popcount
#define gcd __gcd
#define use int T;cin>>T;while(T--)
#define LEN length()
#define all(a) a.begin()+1,a.end()
template<class T> bool mmax(T &u, T v) { return u < v ? (u = v, 1) : 0; }
template<class T> bool mmin(T &u, T v) { return u > v ? (u = v, 1) : 0; }
#define lowbit(x) (x&(-x))
#define yes cout<<"YES"<<'\n'
#define no cout<<"NO"<<'\n'
#define safe_map unordered_map<int, int, custom_hash>
using namespace std;
typedef pair<int,int>pii;
const int N =2e5+7;
struct custom_hash {
size_t operator()(uint64_t x) const {
static const uint64_t FIXED_RANDOM = chrono::steady_clock::now().time_since_epoch().count();
x ^= FIXED_RANDOM;
return x ^ (x >> 16);
}
};
signed main()
{IOSuse{int a,b,m;cin>>a>>b>>m;cout<<m/a+m/b+2<<endl;}return 0;
}C. Left and Right Houses

题目分析:
给定字符串s,要求将字符串分隔,并且确保满足题目条件,遍历即可
#include<bits/stdc++.h>
#pragma GCC optimize("Ofast")
#define INF 1e18
#define IOS ios::sync_with_stdio(false);cin.tie(0);
#define int long long
#define pb push_back
#define vct vector
#define checkbit __builtin_popcount
#define gcd __gcd
#define use int T;cin>>T;while(T--)
#define LEN length()
#define all(a) a.begin()+1,a.end()
template<class T> bool mmax(T &u, T v) { return u < v ? (u = v, 1) : 0; }
template<class T> bool mmin(T &u, T v) { return u > v ? (u = v, 1) : 0; }
#define lowbit(x) (x&(-x))
#define yes cout<<"YES"<<'\n'
#define no cout<<"NO"<<'\n'
#define safe_map unordered_map<int, int, custom_hash>
using namespace std;
typedef pair<int,int>pii;
const int N =2e5+7;
struct custom_hash {
size_t operator()(uint64_t x) const {
static const uint64_t FIXED_RANDOM = chrono::steady_clock::now().time_since_epoch().count();
x ^= FIXED_RANDOM;
return x ^ (x >> 16);
}
};
char s[3000005];
int s1[300005];
signed main()
{
use{int n;cin>>n;scanf("%s",s+1);for(int i=1;i<=n;i++)s1[i]=s1[i-1]+(s[i]-48);int ans=-1;for(int i=0;i<=n;i++)if(s1[i]<=i-s1[i] && s1[n]-s1[i]>=(n-i)-(s1[n]-s1[i])){if(abs(n-i-i)<abs(n-ans-ans))ans=i;}cout<<ans<<endl;
}return 0;
}D. Seraphim the Owl

题目分析:
当主人公在i位置时,他想要换到j位置,首先需要花费 a[j] 元, 并且需要花费
因为主人公需要至少排在第m位,所以在n+1~m-1之间我们可以选择最优值,也就是min(a[i],b[i]),
到m后,我们可以选择a[m]来停下,但是考虑到有可能到前面的位置花费会更小所以我们再向前模拟,更新最小值
#include<bits/stdc++.h>
#pragma GCC optimize("Ofast")
#define INF 1e18
#define IOS ios::sync_with_stdio(false);cin.tie(0);
#define int long long
#define pb push_back
#define vct vector
#define checkbit __builtin_popcount
#define gcd __gcd
#define use int T;cin>>T;while(T--)
#define LEN length()
#define all(a) a.begin()+1,a.end()
template<class T> bool mmax(T &u, T v) { return u < v ? (u = v, 1) : 0; }
template<class T> bool mmin(T &u, T v) { return u > v ? (u = v, 1) : 0; }
#define lowbit(x) (x&(-x))
#define yes cout<<"YES"<<'\n'
#define no cout<<"NO"<<'\n'
#define safe_map unordered_map<int, int, custom_hash>
using namespace std;
typedef pair<int,int>pii;
const int N =2e5+7;
struct custom_hash {
size_t operator()(uint64_t x) const {
static const uint64_t FIXED_RANDOM = chrono::steady_clock::now().time_since_epoch().count();
x ^= FIXED_RANDOM;
return x ^ (x >> 16);
}
};
signed main()
{IOSuse{int n,m;cin>>n>>m;vct<int>a(n+1),b(n+1);for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++)cin>>b[i];int ans=0;for(int i=n;i>m;i--){ans+=min(a[i],b[i]);}int mins=a[m];int x=0;for(int i=m;i>1;i--){x+=b[i];mmin(mins,x+a[i-1]);}cout<<ans+mins<<'\n';}return 0;
}E. Binary Search

题目分析:
二分但没完全二分,数组的取值为1~n,且可能不单调,题目给出的方法适用于单调递增,故,如果起初数组为单调递增的话操作数为0,否则,我们按照题意进行二分模拟,最终二分出来的坐标l 与x起初的位置换一次即可;
证明可行性,因在原数组模拟的情况下,在过程中l满足小于等于x的性质,x也同样满足小于等于x的性质,故可等价替换,故仅需要一次操作即可二分得到x
#include<bits/stdc++.h>
#pragma GCC optimize("Ofast")
#define INF 1e18
#define IOS ios::sync_with_stdio(false);cin.tie(0);
#define int long long
#define pb push_back
#define vct vector
#define checkbit __builtin_popcount
#define gcd __gcd
#define use int T;cin>>T;while(T--)
#define LEN length()
#define all(a) a.begin()+1,a.end()
template<class T> bool mmax(T &u, T v) { return u < v ? (u = v, 1) : 0; }
template<class T> bool mmin(T &u, T v) { return u > v ? (u = v, 1) : 0; }
#define lowbit(x) (x&(-x))
#define yes cout<<"YES"<<'\n'
#define no cout<<"NO"<<'\n'
#define safe_map unordered_map<int, int, custom_hash>
using namespace std;
typedef pair<int,int>pii;
const int N =2e5+7;
struct custom_hash {
size_t operator()(uint64_t x) const {
static const uint64_t FIXED_RANDOM = chrono::steady_clock::now().time_since_epoch().count();
x ^= FIXED_RANDOM;
return x ^ (x >> 16);
}
};
signed main()
{IOSuse{int n,x;cin>>n>>x;vct<int>a(n+1);int cnt=0;safe_map mp;for(int i=1;i<=n;i++){cin>>a[i];mp[a[i]]=i;}if(is_sorted(all(a)))cout<<"0"<<endl;else {cout<<"1"<<endl;int l=1,r=n+1;while(l<r-1){int mid =(l+r)>>1;if(a[mid]>x)r=mid;else l=mid;}cout<<l<<" "<<mp[x]<<endl;}}return 0;
}总结:A~E题都可以用模拟or 思维解出.
相关文章:

Codeforces Round 935 (Div. 3)A~E
A. Setting up Camp 题目分析: 有三种人,内向、外向、综合,内向必须独自一个帐篷,外向必须3个人一个帐篷,综合介于1~3人一个帐篷,我们发现非法情况只会存在外向的人凑不成3个人一个帐篷的情况,因外向不够可…...

ES: spring boot中使用ElasticsearchClient
一、依赖:(要根据不同版本的ES来调整依赖,否则会报错,不支持太低版本的ES,比如7.6以下的) <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-e…...

实体框架EF(Entity Framework)简介
实体框架EF(Entity Framework)简介 文章目录 实体框架EF(Entity Framework)简介一、概述二、O/R Mapping是什么采用O/R Mapping带来哪些好处 三、Entity Framework架构3.1 下图展示了Entity Framework的整体架构3.2 Entity Framew…...

使用CUDA 为Tegra构建OpenCV
返回:OpenCV系列文章目录(持续更新中......) 上一篇:MultiArch与Ubuntu/Debian 的交叉编译 下一篇:在iOS中安装 警告: 本教程可能包含过时的信息。 使用CUDA for Tegra 的OpenCV 本文档是构建支持 CUD…...
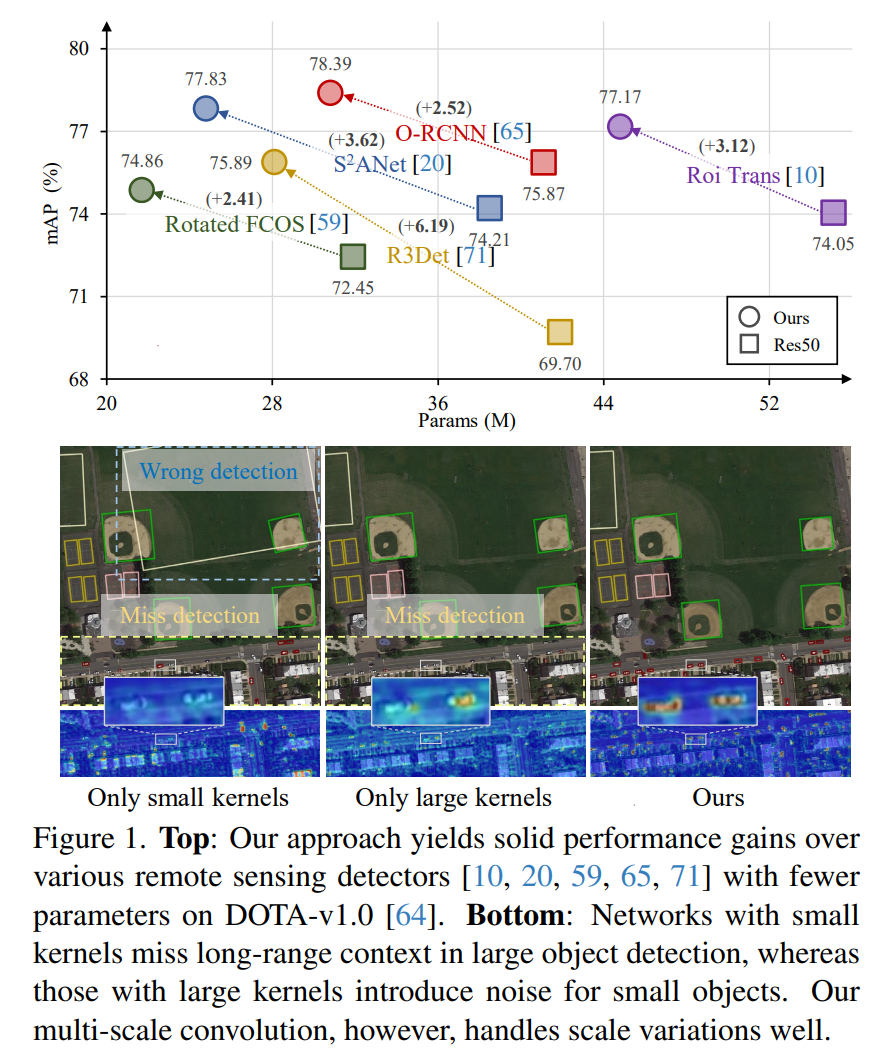
YoloV8改进策略:BackBone改进|PKINet
摘要 PKINet是面向遥感旋转框的主干,网络包含了CAA、PKI等模块,给我们改进卷积结构的模型带来了很多启发。本文,使用PKINet替代YoloV8的主干网络,实现涨点。PKINet是我在作者的模型基础上,重新修改了底层的模块,方便大家轻松移植到YoloV8上。 论文:《Poly Kernel Ince…...
如何在Linux系统部署Dupal CMS结合内网穿透实现无公网IP访问web界面
文章目录 前言1. Docker安装Drupal2. 本地局域网访问3 . Linux 安装cpolar4. 配置Drupal公网访问地址5. 公网远程访问Drupal6. 固定Drupal 公网地址 正文开始前给大家推荐个网站,前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默&a…...

小巧玲珑的SQLite
SQLite是桌面端和移动端的不错选择 前言 SQLite身影无处不在。 SQLite,是一款轻型的数据库,是遵守ACID的关系型数据库管理系统,它的设计目标是嵌入式的,而且目前已经在很多嵌入式产品中使用了它,它占用资源非常的低&a…...

【Android 内存优化】 native内存泄漏监控方案源码分析
文章目录 前言使用效果使用apiJNI的动态注册native方法动态注册 hook的实现android_dlopen_ext和dl_iterate_phdr naive监控的实现nativeGetLeakAllocs 总结 前言 Android的native泄漏怎么检测?下面通过研究开源项目KOOM来一探究竟。 使用效果 未触发泄漏前的日志…...
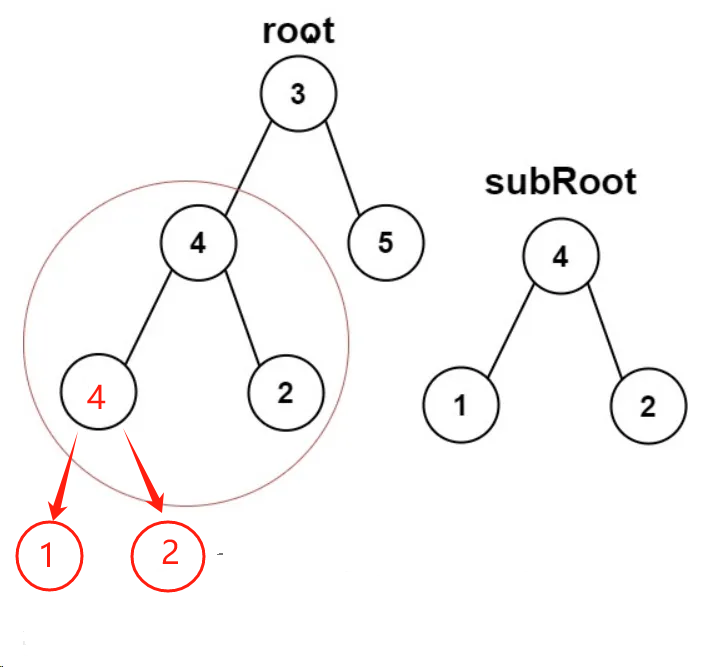
数据结构 二叉树 力扣例题AC——代码以及思路记录
LCR 175. 计算二叉树的深 某公司架构以二叉树形式记录,请返回该公司的层级数。 AC int calculateDepth(struct TreeNode* root) {if (root NULL){return 0;}else{return 1 fmax(calculateDepth(root->left), calculateDepth(root->right));} } 代码思路 …...

Android 11系统启动流程
在Android 11系统启动流程中,系统启动主要经历了以下几个阶段: 引导加载程序(Bootloader)启动: 当设备加电后,首先运行的是ROM Bootloader,它负责验证操作系统映像的完整性、初始化基本硬件并加…...
python 爬取杭州小区挂牌均价
下载chrome驱动 通过chrome浏览器的 设置-帮助-关于Google Chrome 查看你所使用的Chrome版本 驱动可以从这两个地方找: 【推荐】https://storage.googleapis.com/chrome-for-testing-publichttp://npm.taobao.org/mirrors/chromedriver import zipfile import os import r…...
数据可视化-ECharts Html项目实战(3)
在之前的文章中,我们学习了如何创建堆积折线图,饼图以及较难的瀑布图并更改图标标题。想了解的朋友可以查看这篇文章。同时,希望我的文章能帮助到你,如果觉得我的文章写的不错,请留下你宝贵的点赞,谢谢。 …...
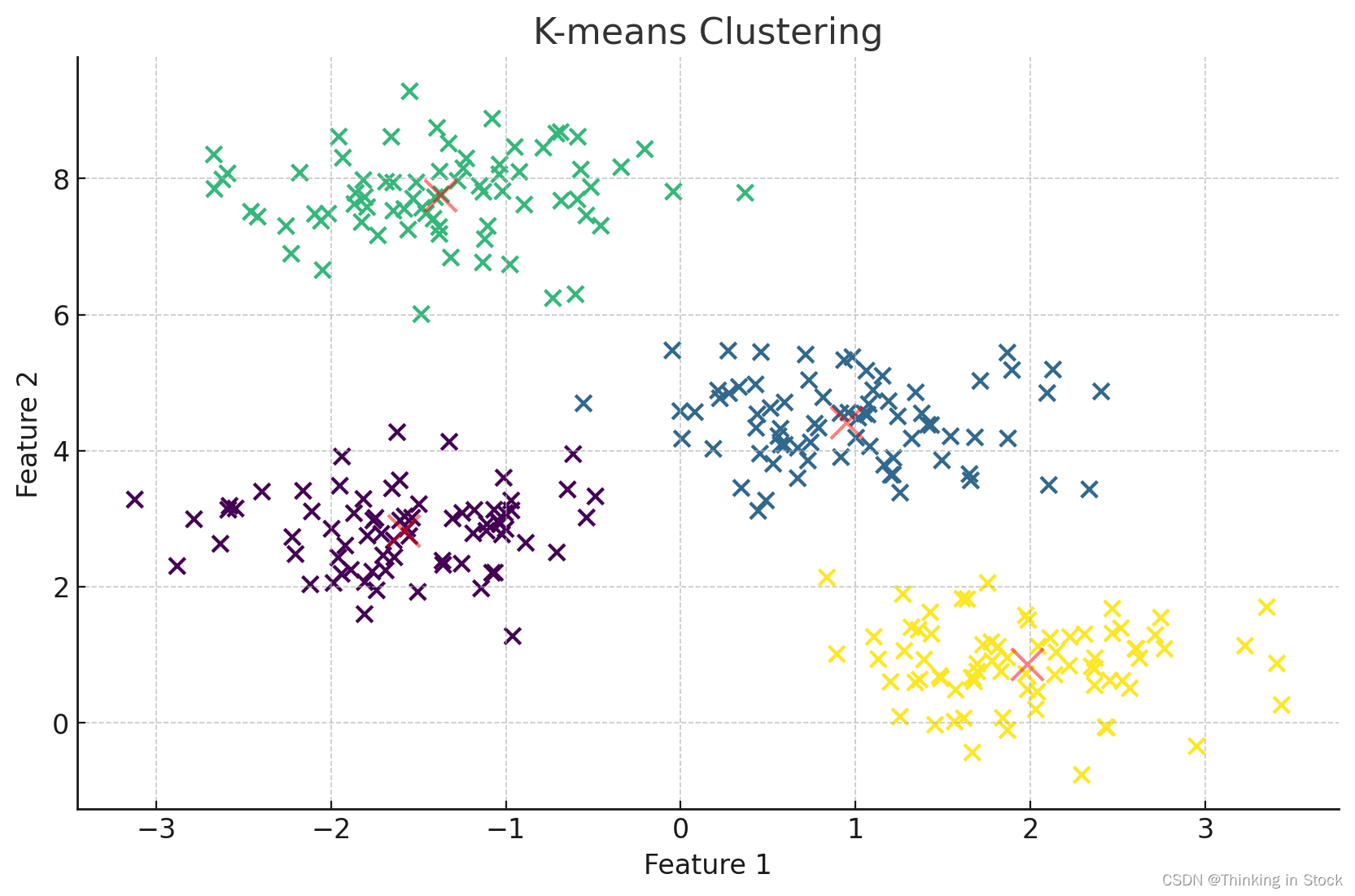
【理解机器学习算法】之Clustering算法(K-Means)
实现 K-means 聚类从零开始涉及几个关键步骤:初始化质心、将点分配给最近的质心、根据分配更新质心,以及重复这个过程直到收敛。这里是一个基本的 Python 实现: K-means 算法步骤: 初始化质心:从数据点中随机选择 k …...
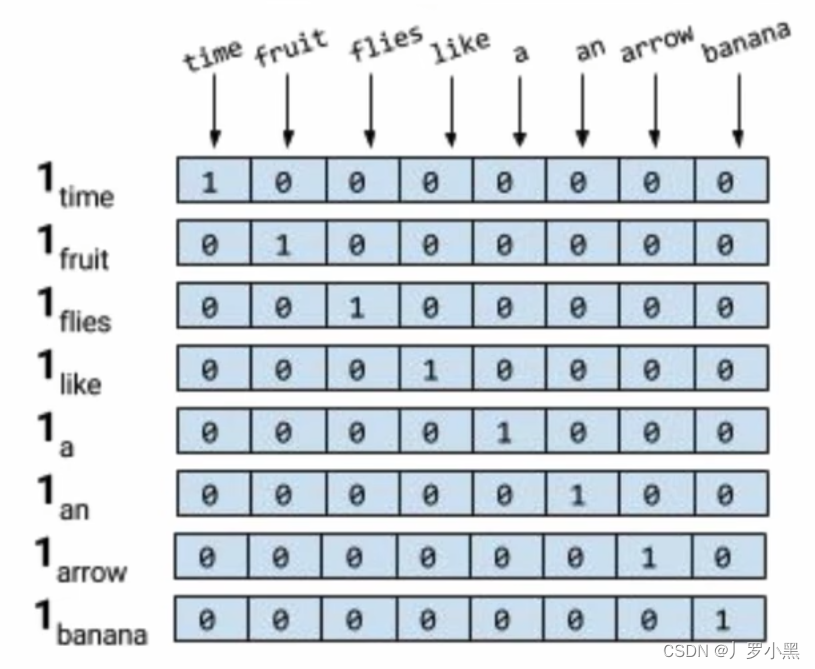
Transformer的前世今生 day02(神经网络语言模型、词向量)
神经网络语言模型 使用神经网络的方法,去完成语言模型的两个问题,下图为两层感知机的神经网络语言模型: 假设词典V内有五个词:“判断”、“这个”、“词”、“的”、“词性”,且要输出P(w_next | “判断”、“这个”、…...

【Linux】多线程编程基础
💻文章目录 📄前言🌺linux线程基础线程的概念线程的优缺点线程与进程的区别 线程的创建 🌻linux线程冲突概念互斥锁函数介绍加锁的缺点 📓总结 📄前言 无论你是否为程序员,相信多线程这个词汇应…...
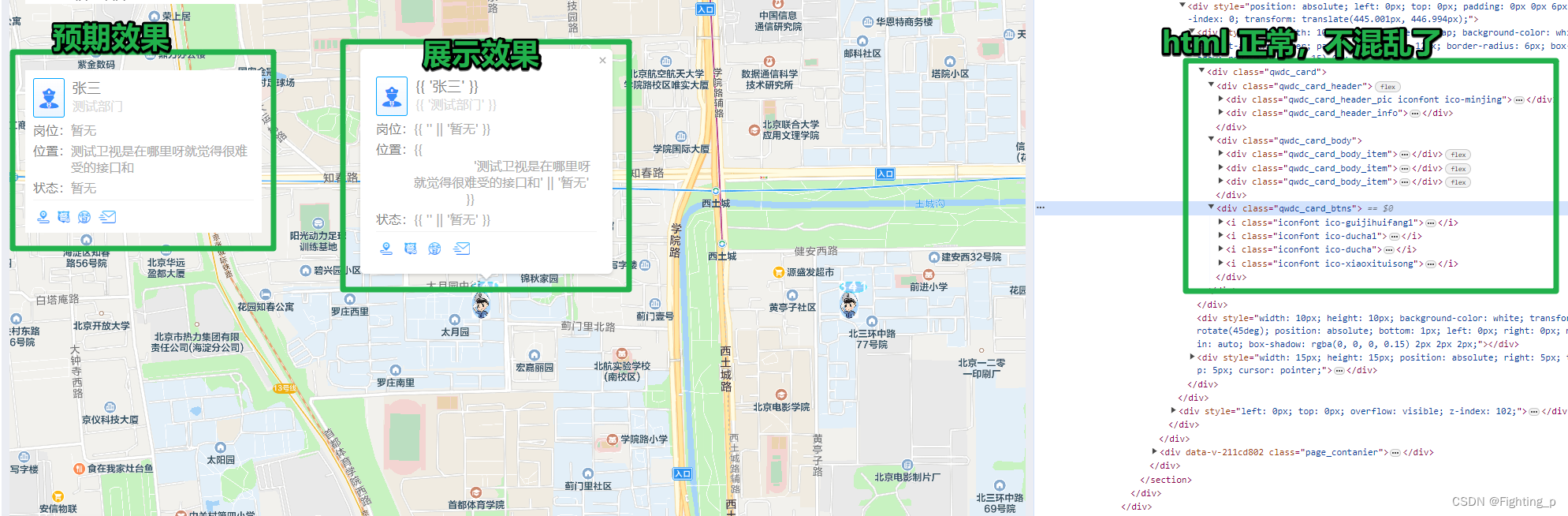
【地图】腾讯地图 - InfoWindow 自定义信息窗口内容时,内容 html 嵌套混乱问题
目录 需求描述问题问题代码页面展示 解决原因解决办法解决代码页面展示 代码汇总注 需求描述 腾讯地图上画点位,点击点位展示弹框信息 问题 问题代码 // 打开弹框 openInfoWindow(position, content) {this.infoWindow new TMap.InfoWindow({map: this.map,posit…...

Vue3、element-plus和Vue2、elementUI的一些转换
插槽 Vue3<template #default"scope"></template> <template #footer></template>Vue2<template slot-scope"scope"></template> <template slot"footer"></template>JS定义 Vue3 <script…...
Go语言gin框架中加载html/css/js等静态资源
Gin框架没有内置静态文件服务,但可以使用gin.Static或gin.StaticFS中间件来提供静态文件服务。 效果图如下: 一、gin 框架加载 Html 模板文件的方法 方式1:加载单个或多个html文件,需要指明具体文件名 r.LoadHTMLFiles("vie…...

#鸿蒙生态创新中心#揭幕仪式在深圳湾科技生态园举行
3 月 19 日,#鸿蒙生态创新中心#揭幕仪式在深圳湾科技生态园举行。 现场,深圳市南山区人民政府副区长李志娜发布《2024 年南山区支持鸿蒙原生应用发展首批政策措施清单》,从加强鸿蒙原生应用供给能力、推动鸿蒙原生应用产业集聚、完善鸿蒙原生…...

flask 继续学习
group_by group_by是一种在数据库查询或数据处理中常用的操作,它用于将数据按照指定的列进行分组。通过group_by操作,可以将数据集按照某个列的值进行分类,然后对每个分类进行聚合计算或其他操作。 在SQL语言中,group_by通常与聚…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
