DP:斐波那契数列模型
创作不易,感谢三连支持 !
斐波那契数列用于一维探索的单峰函数之中,用于求解最优值的方法。其主要优势为,在第一次迭代的时候求解两个函数值,之后每次迭代只需求解一次 。
一、第N个泰波那契数
. - 力扣(LeetCode)第N个泰波那契数

class Solution {
public:int tribonacci(int n) {//边界情况if(n==0||n==1) return n;if(n==2) return 1;//建表vector<int> dp(n+1);dp[1]=dp[2]=1;//开始填表for(int i=3;i<=n;++i) dp[i]=dp[i-1]+dp[i-2]+dp[i-3];return dp[n];}
};时间复杂度O(N),空间复杂度为O(N)
是否还有可以优化的方法呢??那就是该题可以使用滚动数组!

class Solution {
public:int tribonacci(int n) {//边界情况if(n==0||n==1) return n;if(n==2) return 1;//滚动数组int a=0,b=1,c=1,d=0;//开始滚动for(int i=3;i<=n;++i) {d=a+b+c;a=b;b=c;c=d;}return d;}
};时间复杂度O(N),空间复杂度为O(1)
二、三步问题
. - 力扣(LeetCode)三步问题
思路1:dp[i]表示从起点到达i位置一共有几种方法

class Solution {
public:int waysToStep(int n) {const int MOD=1e9+7;//边界情况if(n==1||n==2) return n;if(n==3) return 4;//建立dp表vector<int> dp(n+1);//初始化dp[1]=1,dp[2]=2,dp[3]=4;//填表for(int i=4;i<=n;++i) dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;return dp[n];}
};思路2:dp[i]表示从i位置到达终点一共有几种方法

class Solution {
public:int waysToStep(int n) {const int MOD=1e9+7;//边界情况if(n==1||n==2) return n;if(n==3) return 4;//建立dp表vector<int> dp(n);//初始化dp[n-1]=1,dp[n-2]=2,dp[n-3]=4;//填表for(int i=n-4;i>=0;--i) dp[i]=((dp[i+1]+dp[i+2])%MOD+dp[i+3])%MOD;return dp[0];}
};三、使用最小的花费爬楼梯
. - 力扣(LeetCode)使用最小的花费爬楼梯
方法1:dp[i]表示从起点到i台阶的最小花费

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n+1);//开始填表for(int i=2;i<=n;++i) dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);return dp[n];}
};思路2:我们也可以以i为起点,让dp[i]表示到楼顶的最小花费

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();//处理边界情况vector<int> dp(n);dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];for(int i=n-3;i>=0;--i) dp[i]=cost[i]+min(dp[i+1],dp[i+2]);return min(dp[0],dp[1]);}
};四、解码方法
. - 力扣(LeetCode)解码方法

class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int> dp(n);if(s[0]!='0') ++dp[0];//处理边界情况if(n==1) return dp[0];if(s[1]!='0'&&s[0]!='0') dp[1]++;int t=(s[0]-'0')*10+(s[1]-'0');if(10<=t&&t<=26) ++dp[1];//开始填表for(int i=2;i<n;++i) {if(s[i]!='0') dp[i]+=dp[i-1];int t=(s[i-1]-'0')*10+(s[i]-'0');if(10<=t&&t<=26) dp[i]+=dp[i-2];}return dp[n-1];}
};我们会发现dp[1]的初始化和填表里面的过程非常相似,所以我们可以用一个动态规划的小技巧——虚拟节点(专门用来处理边界问题)

class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int> dp(n+1);dp[0]=1;if(s[0]!='0') ++dp[1];//开始填表for(int i=2;i<=n;++i) {if(s[i-1]!='0') dp[i]+=dp[i-1];int t=(s[i-2]-'0')*10+(s[i-1]-'0');if(10<=t&&t<=26) dp[i]+=dp[i-2];}return dp[n];}
};先暂时更新到这,后面有新的题目会持续更新
相关文章:

DP:斐波那契数列模型
创作不易,感谢三连支持 ! 斐波那契数列用于一维探索的单峰函数之中,用于求解最优值的方法。其主要优势为,在第一次迭代的时候求解两个函数值,之后每次迭代只需求解一次 。 一、第N个泰波那契数 . - 力扣(…...
----prmise)
JavaScript高级(十四)----prmise
异步请求的处理方式 回调函数 所谓的回调函数就是函数作为参数的传递,在一个函数内部调用另一个函数,调用的同时可以把内部函数的数据传递出来,他的使用场景就是异步操作,数据需要等待一段时间才能返回的情况下可以使用回调函数…...

28 OpenCV 轮廓周围绘制图形
文章目录 approxPolyDP 轮廓周围绘制矩形boundingRectminAreaRect绘制圆和椭圆示例 approxPolyDP 轮廓周围绘制矩形 approxPolyDP(InputArray curve, OutputArray approxCurve, double epsilon, bool closed)curve:输入点集,二维点向量的集合appro…...

校企合作,助力人才培养——黄冈师范学院-唯众 “实习实训基地”揭牌仪式顺利举行
3月20日上午,黄冈师范学院计算机学院院长何中林、教务处实习科科长雷汝琳以及计算机学院实验室主任肖飞一行三人,莅临唯众进行参观交流。唯众总经理冉柏权、销售总监舒敏以及董事长助理代西凯进行了热情接待。双方就如何更好地结合企业需求与学院教育资源…...

npm audit fix --force
npm audit fix --force是npm的一个命令,用于自动修复包中的安全漏洞。 其中: - npm audit:审查项目中的依赖包,检查是否存在已知的安全漏洞。 - fix:自动安装相关的补丁来修复发现的漏洞。 - --force:强制安装补丁版本,即使出现不兼容也强制更新。 所以npm audit fix --fo…...
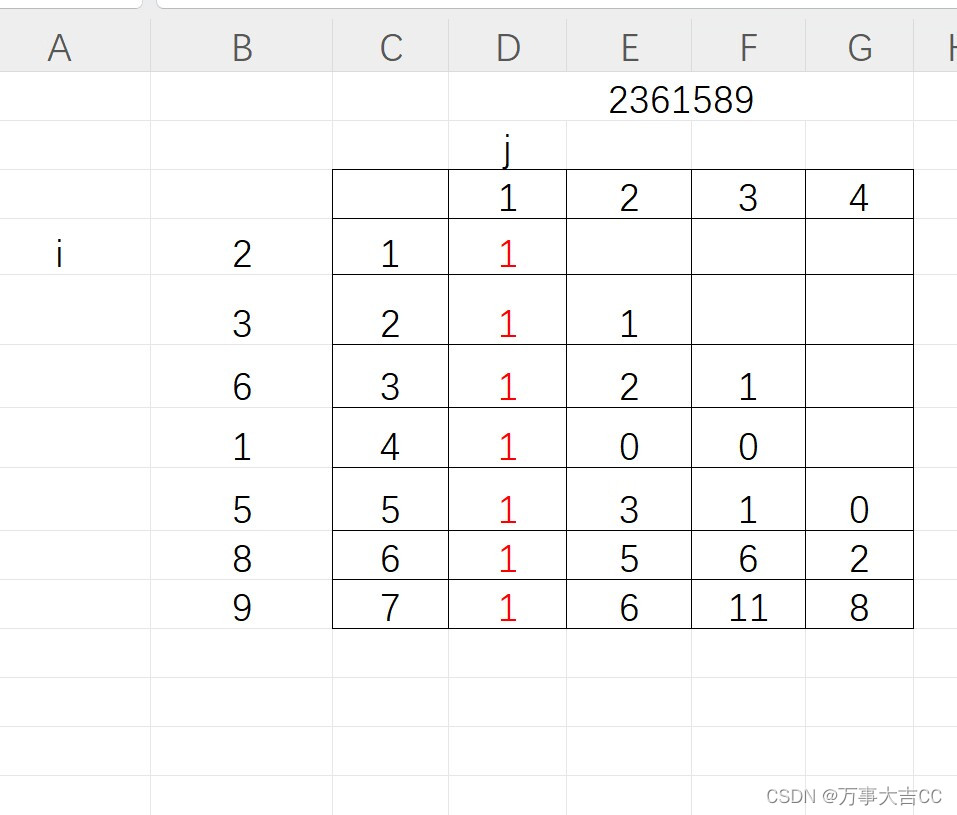
递增四元组
解法: 首先都可以想到dp[i]:第i个元素结尾的递增四元组有dp[i]个 然后发现有一组数据:2,3,6,1,5,8。会出现6结尾和5结尾的递增三元组,也就是未来的决策受过去影响,专业的说就是有后效性。需要强化约束条件࿰…...

蓝桥杯每日一题——棋盘
问题描述 小蓝拥有 n xn 大小的棋盘,一开始棋盘上全都是白子。小蓝进行了 m 次操作,每次操作会将棋盘上某个范围内的所有棋子的颜色取反(也就是白色棋子变为黑色,黑色棋子变为白色)请输出所有操作做完后棋盘上每个棋子的颜色。输入格式 输入的…...
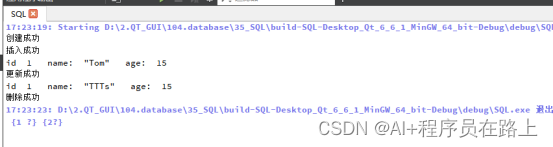
QT6实现创建与操作sqlite数据库及读取实例(一)
一.Qt为SQL数据库提供支持的基本模块(Qt SQL) Qt SQL的API分为不同层: 驱动层 SQL API层 用户接口层 1.驱动层 对于Qt 是基于C来实现的框架,该层主要包括QSqlDriver,QSqlDriverCreator,QSqlDriverCreatorBase,QSqlPlug…...
第十四届蓝桥杯JavaB组省赛真题 - 阶乘求和
/ 10^9考虑前九位,% 10^9保留后9位 解题思路: 求获取结果的后九位数字,需要对10^9取余,因为202320232023这个数字的阶乘太大,必须要减少计算量,因为当一个整数乘以10^9后对其取余,那么结果都为0。 所以我…...

Java毕业设计 基于springboot医院挂号系统 医院管理系统
Java毕业设计 基于springboot医院挂号系统 医院管理系统 springboot医院挂号系统 医院管理系统 功能介绍 用户:登录 首页 个人资料 修改密码 门诊管理 用户挂号 医生:登录 首页 个人资料 修改密码 门诊管理: 用户挂号 处方划价 项目划价 项目缴费 项目…...
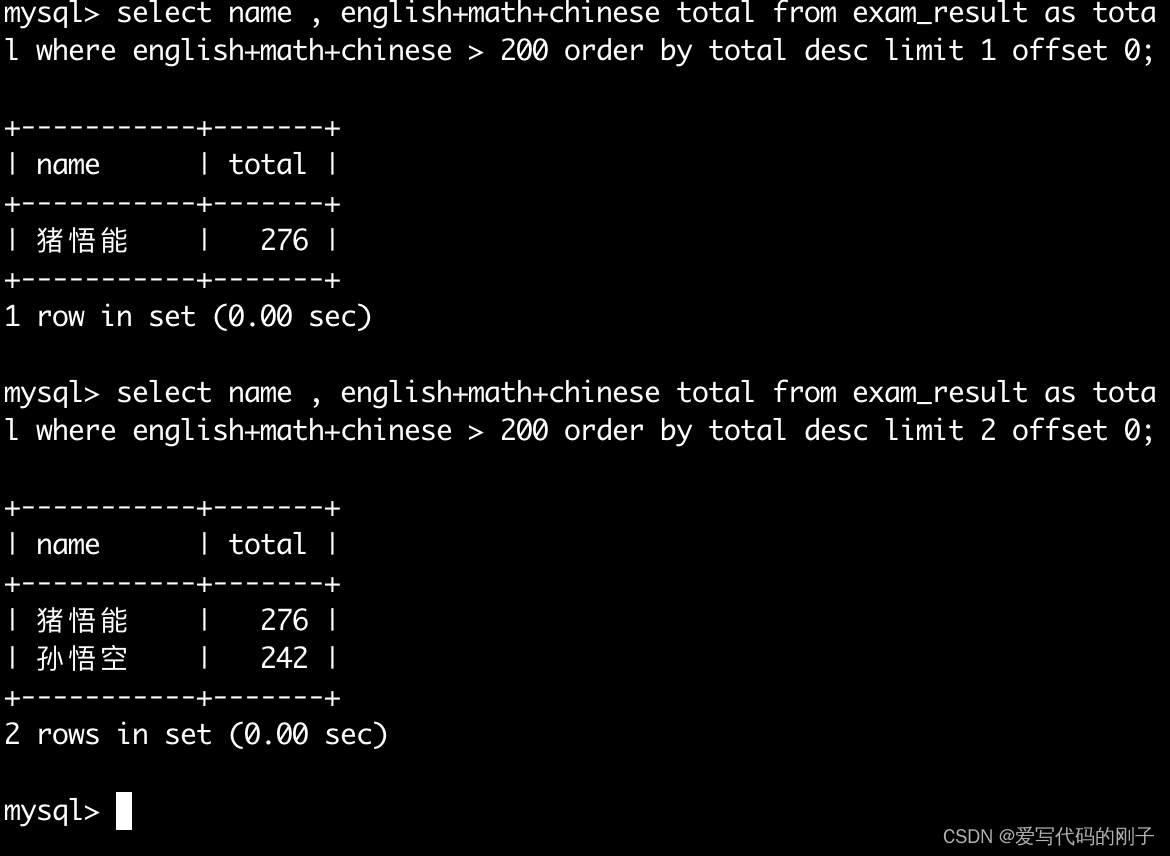
【MySQL】基本查询(1)
【MySQL】基本查询(1) 目录 【MySQL】基本查询(1)表的增删改查Create单行数据 全列插入多行数据 指定列插入插入否则更新替换 RetrieveSELECT 列全列查询指定列查询查询字段为表达式为查询结果指定别名结果去重 WHERE 条件英语不…...
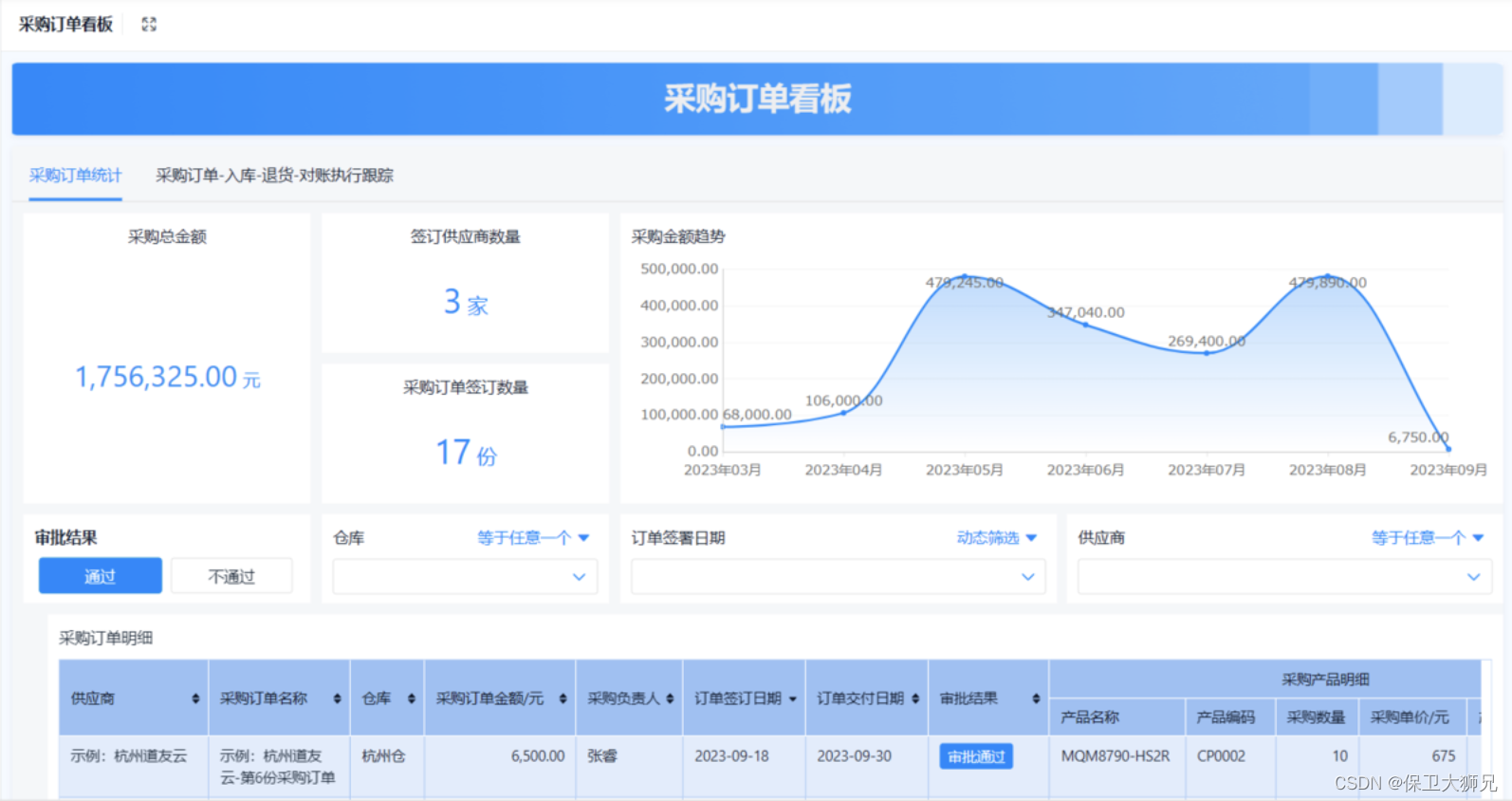
一文讲清!进销存管理系统如何实现锁库及库存冻结?计算月加权平均成本?
进销存管理系统中的锁库及库存冻结如何实现?进销存管理系统如何计算月加权平均成本?进销存管理系统又该如何统计和预测采购需求?这些进销存管理难题困扰着许多企业管理者。本文将结合数年从业经验,深入探讨这些进销存管理难题&…...
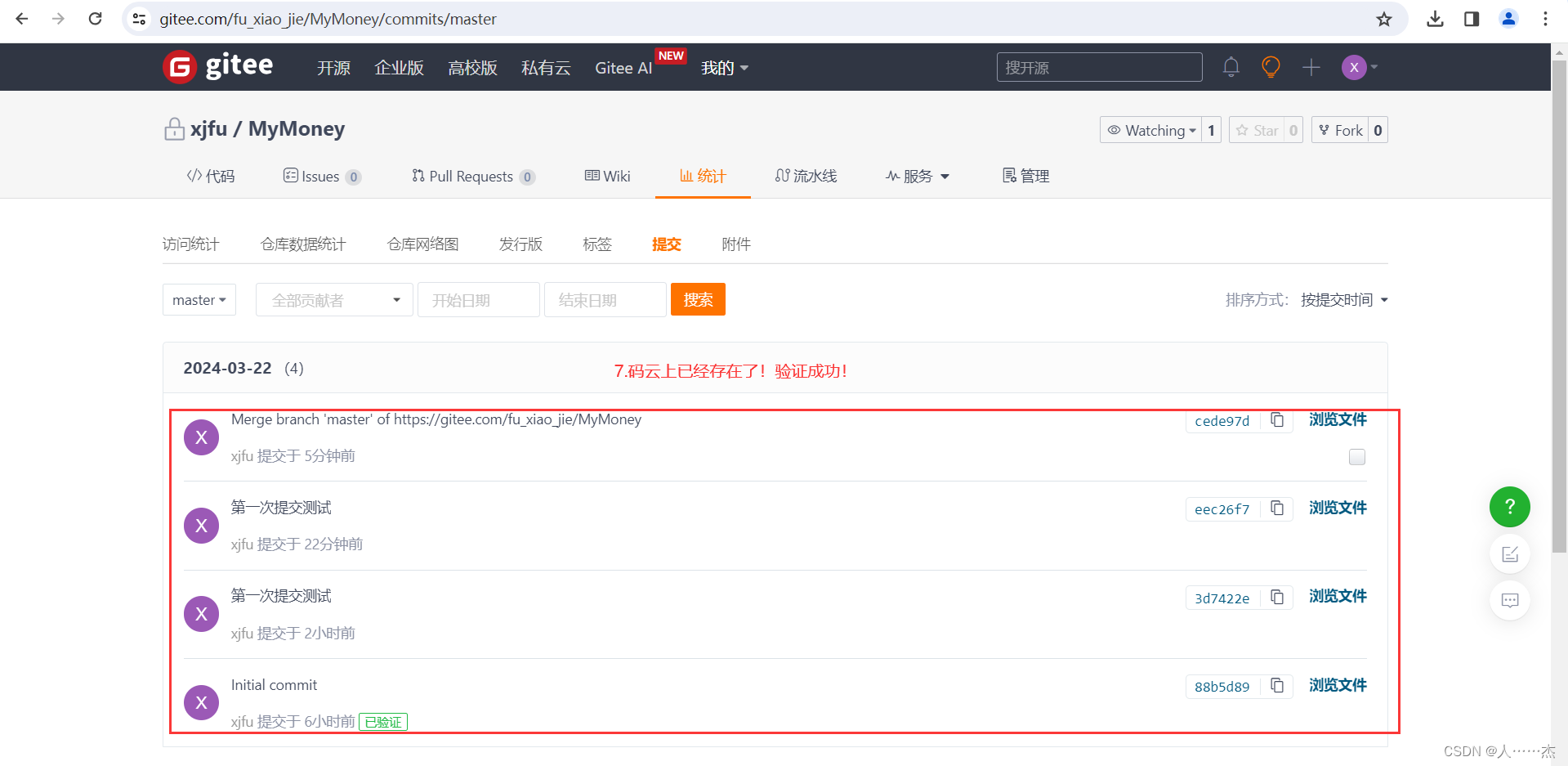
将本地项目上传至码云
1.打开git,然后进入到项目目录 2.进入到项目目录,然后进行git的初始化 成功后本地项目目录内会多出一个“.git”文件: 指令介绍: git init -- 建立本地仓库 3.在码云上创建仓库,名为“MyMoney” 创建过程参考&…...
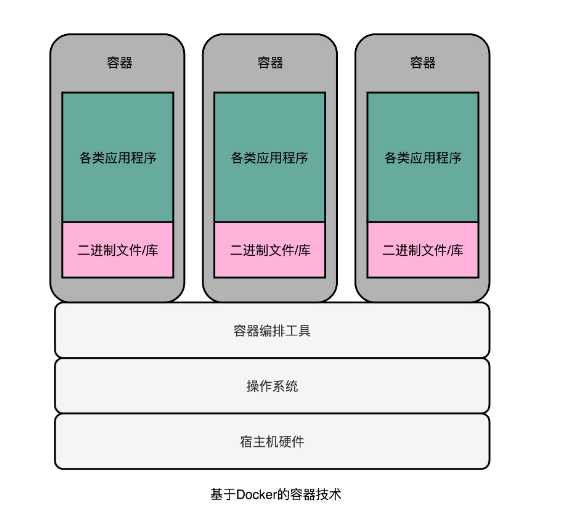
虚拟化技术
前言 大家好我是jiantaoyab,这是我所总结作为学习的笔记第十八篇,在这里分享给大家,这篇文章讲虚拟技术就是大家平时用到的云服务器是什么。 虚拟机技术变迁 虚拟机(Virtual Machine)技术,其实就是指在现…...

鸿蒙一次开发,多端部署(一)简介
背景 随着终端设备形态日益多样化,分布式技术逐渐打破单一硬件边界,一个应用或服务,可以在不同的硬件设备之间随意调用、互助共享,让用户享受无缝的全场景体验。而作为应用开发者,广泛的设备类型也能为应用带来广大的…...
)
数据结构——单向链表(C语言版)
在数据结构和算法中,链表是一种常见的数据结构,它由一系列节点组成,每个节点包含数据和指向下一个节点的指针。在C语言中,我们可以使用指针来实现单向链表。下面将详细介绍如何用C语言实现单向链表。 目录 1. 定义节点结构体 2. …...
ideaSSM 工厂效能管理系统bootstrap开发mysql数据库web结构java编程计算机网页源码maven项目
一、源码特点 idea 开发 SSM 工厂效能管理系统是一套完善的信息管理系统,结合SSM框架和bootstrap完成本系统,对理解JSP java编程开发语言有帮助系统采用SSM框架(MVC模式开发),系统具有完整的源代码和数据库ÿ…...

Java反射机制的讲解及其示例说明
Java 反射机制是指在运行时动态地获取类的信息以及操作对象的方式。它允许程序在运行时检查和操作类、方法、属性等,而不需要在编译时就确定这些属性。通过反射机制,我们可以在运行时动态地创建对象、调用方法、获取属性等。 Java 反射机制提供了以下主…...

20240309web前端_第二周作业_完成游戏导航栏
作业:游戏导航栏 成果展示: 完整代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0…...

五、大模型-Prompt
一、prompt是什么 在大型语言模型集成中,"prompt" 是指您向模型提供的输入文本或指令,以引导模型生成特定类型的响应。这个 prompt 可以是一个问题、一段描述、一个任务说明,甚至是一部分对话历史记录等。通过设计和优化 prompt&a…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

