计算地球圆盘负荷产生的位移
1.研究背景
计算受表面载荷影响的弹性体变形问题有着悠久的历史,涉及到许多著名的数学家和物理学家(Boussinesq 1885;Lamb 1901;Love 1911,1929;Shida 1912;Terazawa 1916;Munk & MacDonald 1960;Longman 1962,1963;Farrell 1972)。对于均匀弹性半空间的易于编码的解(Becker & Bevis 2004)在许多工程上是有用的,但在地球不是半空间也不均匀的地质应用中通常不适用。对于分层弹性半空间的解(例如Pan等人2007),其适用范围更广,但即使对于具有大孔径的载荷或在离载荷远处计算变形时,这种形式主义也不合适,这里所说的“大”是指距离地球半径的显著部分或更大的距离。因此,大多数地球物理应用的首选框架是分层、弹性、自引力球体和液态核心(Farrell 1972)。这个问题的解通常都是在涉及到载荷Love数的展开式中进行的,通常用符号(hn,kn,ln)来表示。通常,这些处理采用点载荷或圆盘载荷。
点载荷形式主义在接近标称点载荷时通常无效,从这个意义上讲,圆盘载荷形式主义更灵活。我们注意到,Love数形式主义适用于球对称弹性地球模型;横向各向同性可以被纳入这类模型,只要它符合球对称性(Pan等人2015)。弹性各向异性的一般类(例如横向变化的各向异性和方位各向异性)打破了球对称性,在这种情况下,Love数方法就不再适用,需要使用不同的方法,例如自引力有限元模型(虽然它们也存在自己的计算困难)。使用本文中提出的方程和代码的人隐含地假设弹性各向异性要么不存在,要么是一种非常特殊的类型。
在1975年至2000年期间,关于表面载荷问题的地球物理文献大多集中在冰盖地壳回弹调整方面,这涉及到粘弹性地球的载荷响应(Haskell 1935;Cathles 1975;Peltier & Andrews 1976;Wu & Peltier 1982)。几乎所有这些研究都使用了Love数形式主义。载荷问题的线性弹性和线性粘弹性版本通过弹性-粘弹性对应原理相互联系(Alfrey 1944;Read 1950;Lee 1950)。但是,从2001年开始,人们对纯弹性问题的兴趣出现了重大回升。这是因为(i)大地测量学家和地球物理学家开始意识到全球定位系统(GPS)接收机网络,以及更近期的全球导航卫星系统(GNSS)接收机,正在记录由水、雪和冰固体地球上的载荷所引起的季节性、持续性(即渐进性)和瞬时的弹性位移(Blewitt等人2001;Heki 2001;Mangiarotti等人2001;Dong等人2002;Bevis等人2005),而且在较小程度上还受大气压力变化的影响(Vandam等人1994),以及(ii)地球弹性变形的大地测量观测可以用于监测冰体质量(Khan等人2010;Bevis等人2012;Nielsen等人2012;Spada等人2012;Nielsen等人2013)和陆地水储存(Bevis等人2004,2005;Steckler等人2010;Fu等人2013;Borsa等人2014)的变化,从而提供了一种研究气候循环和气候变化的新方法。
描述分布式负荷或负荷变化的最简单方法是将其表示为一个或多个圆盘载荷。如果将质量或质量变化场表示为网格,则每个网格单元都可以视为圆盘载荷,或者,如果它位于地球测量站的远场,也可以视为点载荷。点载荷的响应可以与小而远的圆盘载荷的相似,除了在接近点载荷的地方,点载荷概念本身几乎从来不是现实的。本文的目的是两方面的。首先,我们希望向非专家提供有关如何计算地球对圆盘载荷的弹性响应的简单但完整的讨论。我们提供了一个MATLAB函数(diskload)来实现这个算法。我们的代码,像几乎所有它的同类一样,都会求和由载荷Love数和勒让德多项式或勒让德多项式的导数组成的项,其阶数为n = 0、1、2,...nmax。选择适当的nmax值非常重要,特别是当我们寻求对载荷的近场响应的准确估计时。当建模地球测量站位于质量损失正在使用非常高分辨率数字高程模型(DEM)进行表征的冰盖边缘附近时,由于DEM的网格间距或单元大小,适当的nmax值会按比例增加,所以这个错误相当容易发生。我们希望这个讨论能帮助我们的读者更自信地使用更一般和更复杂的软件包,例如REAR(Melini等人2015a,b)。(翻译自Bevis et al., 2016)
2.基本原理
所谓的“圆盘载荷”是一种特定类型的表面质量密度分布,其特点是(i)均匀施加的压力,即恒定的载荷“厚度”,和(ii)轴对称,这两个特点使得圆盘载荷在与冰盖等高度调整相关的应用中非常方便(例如Spada等人2012;Melini等人2015b),因为它可以直接展开成一系列球谐函数。此处略去基本理论公式的推导,感兴趣的参考原文。
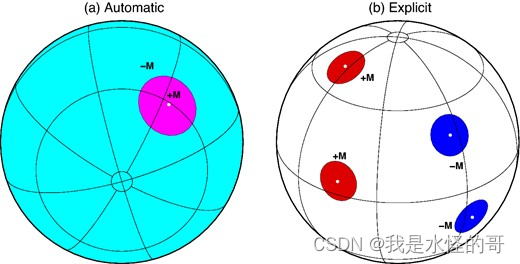
引用至Bevis et al.(2016)
水平和垂直位移计算公式:

3.matlab程序
下载地址:
https://github.com/danielemelini/diskload
diskload MATLAB函数用于计算对施加在给定角半径和高度的圆盘上的均匀表面压力载荷的响应。弹性响应是在地球表面上的一个或多个点上计算的,这些点与圆盘载荷的中心指定的角距离相隔。弹性响应是使用用户提供的弹性负载Love数(h,k,l)计算的,这些Love数是使用特定的地球弹性结构模型生成的。下图是h l k负荷love数随阶数的变化示意图。
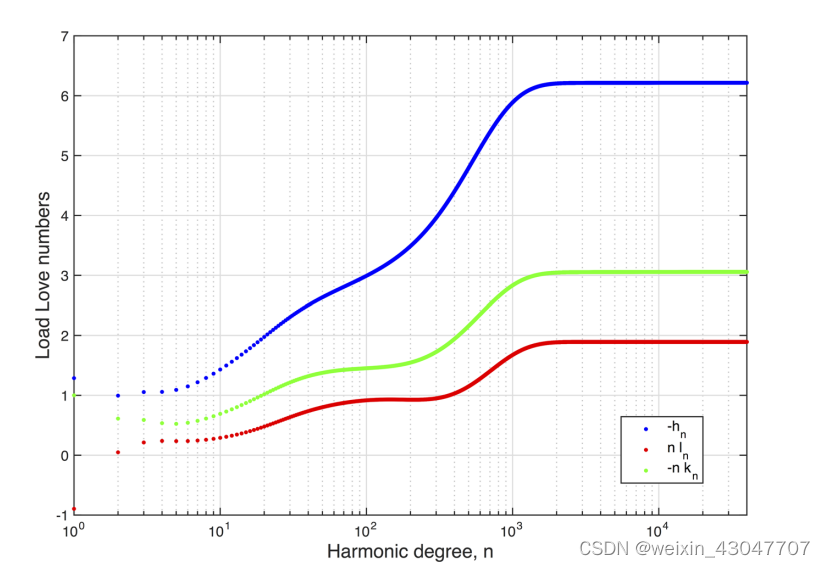
下载程序,在matlab中打开:
clear
%% Load LNs
load REF_6371_loading_love_numbers
%% Set some constants
alpha = 0.1; % Disk radius (degrees)
theta = linspace(0,alpha*5,100); % Range of colatitudes wrt disk center
Tw = 1; % Disk height (equivalent water height, m)
nmin = 0; % Minimum degree
nmax = [100:100:40000]; % Range of maximum degrees
imass = 1; % choose imass,0 or 1 (uncompensated/compensated load)
%%
if imass==1
fprintf('invoking a globally compensated load (icomp=1)\n')
else
fprintf('invoking an uncompensated load (icomp=0)\n')
end
% Compute the disc response for the maximum value of nmax
[U,V,G]= diskload(alpha,imass,theta,Tw,nmin,nmax(end),h_love,k_love,l_love);
%% FIG 1
figure(1); clf;
plot( theta./alpha, U, 'b', 'LineWidth', 1.5 ); hold on;
plot( theta./alpha, V, 'r', 'LineWidth', 1.5 );
plot( theta./alpha, G, 'g', 'LineWidth', 1.5 );
xlabel( '\theta/\alpha', 'FontSize', 16 );
ylabel( 'mm', 'FontSize', 16 );
xlim([0 5]);
ylim([-2.5 1]);
grid on;
legend( 'U', 'V', 'G', 'Location', 'best' );
tit1=['Disk radius \alpha = ',sprintf('%4.2f^\\circ',alpha)];
tit2=[' Load = ',sprintf('%4.2f',alpha),' m w.e.'];
title([tit1 tit2])
%% Examine sensitivity to nmax
% Compute the disc response vs nmax at theta = K * alpha
K=1.5;
[U,V,G]= diskload(alpha,imass,K*alpha,Tw,nmin,nmax,h_love,k_love,l_love);
%% FIG 2
figure(2); clf;
semilogx( nmax, U, 'b', 'LineWidth', 1.5 ); hold on;
semilogx( nmax, V, 'r', 'LineWidth', 1.5 );
semilogx( nmax, G, 'g', 'LineWidth', 1.5 );
xlabel( 'n_{max}', 'FontSize', 16 );
ylabel( 'mm', 'FontSize', 16 );
xlim( [100 40000] );
ylim( [-1 .3] ); % good for K=1.5 or 1.25
%ylim( [-0.6 .2] ); % good for K = 1.75 or 2
nROT = 360 / alpha;
semilogx( [nROT nROT], ylim, 'k-.', 'LineWidth', 1.1 );
semilogx( 2*[nROT nROT], ylim, 'k-.', 'LineWidth', 1.1 );
semilogx(xlim,U(end)*[1 1],'b--', 'LineWidth', 0.5 );
semilogx(xlim,V(end)*[1 1],'r--', 'LineWidth', 0.5 );
semilogx(xlim,G(end)*[1 1],'g--', 'LineWidth', 0.5 );
hold off;
grid on;
legend( 'U', 'V', 'G', 'Location', 'best' );
Ht=title(['Truncation error: Loading response computed',...
' at \theta = ',sprintf('%4.2f',K),...
' \alpha as a function of n_{max} ']);
set(Ht,'FontSize',14)
运行结果:
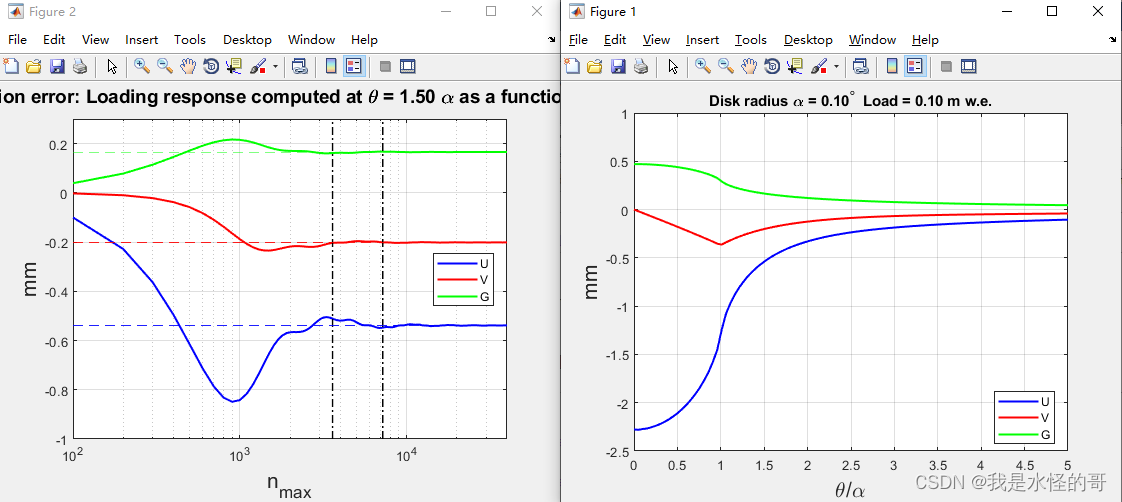
关于负荷变形计算的问题,可以参见以下的文章:
利用GRACE和地表质量模型计算地球弹性负荷变形实验笔记_如何通过grace数据导出位移-CSDN博客
LoadDef python工具包学习二:利用JPL mascon数据计算地表站点的三维变形(E、N、V)_loaddef grace]-CSDN博客
参考文献:
Bevis, M., Melini, D., & Spada, G. (2016). On computing the geoelastic response to a disk load. Geophysical Journal International, 205(3), 1804-1812.
♥欢迎点赞收藏♥
相关文章:

计算地球圆盘负荷产生的位移
1.研究背景 计算受表面载荷影响的弹性体变形问题有着悠久的历史,涉及到许多著名的数学家和物理学家(Boussinesq 1885;Lamb 1901;Love 1911,1929;Shida 1912;Terazawa 1916;Munk &…...

Harbor介绍
1.什么是Harbor Harbor是一个开源的企业级Docker Registry管理项目,由VMware公司开源。 Harbor提供了比Docker官方公共镜像仓库更为丰富和安全的功能,尤其适合企业环境使用。以下是Harbor的一些关键特性: 权限管理(RBAC&#x…...
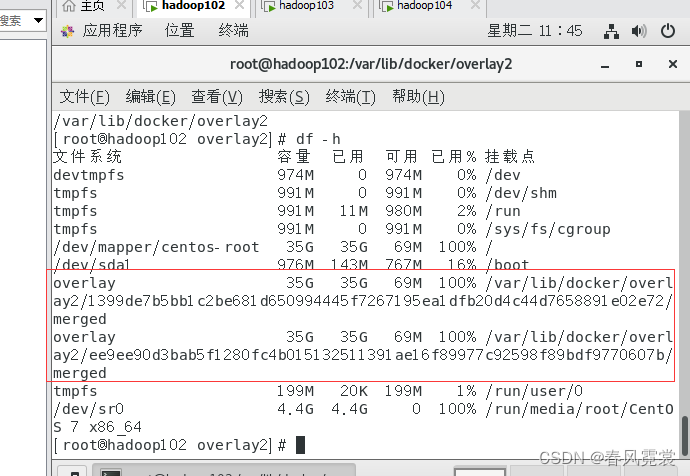
解决jenkins运行磁盘满的问题
参考:https://blog.csdn.net/ouyang_peng/article/details/79225993 分配磁盘空间相关操作: https://cloud.tencent.com/developer/article/2230624 登录jenkins相对应的服务或容器中查看磁盘情况: df -h在102挂载服务器上看到是这两个文件…...

使用echart绘制拓扑图,树类型,自定义tooltip和label样式,可收缩
效果如图: 鼠标移上显示 vue3 - ts文件 “echarts”: “^5.4.3”, import { EChartsOption } from echarts import * as echarts from echarts/core import { TooltipComponent } from echarts/components import { TreeChart } from echarts/charts import { C…...

常用的6个的ChatGPT网站,国内可用!
GPTGod 🌐 链接: GPTGod 🏷️ 标签: GPT-4 免费体验 支持API 支持绘图 付费选项 📝 简介:GPTGod 是一个功能全面的平台,提供GPT-4的强大功能,包括API接入和绘图支持。用户可以选择免…...

Linux课程____Samba文件共享服务
一、 Samba服务基础 SMB协议,服务消息块 CIFS协议,通用互联网文件系统 1.Samba 服务器的主要程序 smbd:提供对服务器中文件、打印资源的共享访问 nmbd:提供基于 NetBlOS 主机名称的解析 2.目录文件 /etc/samba/smb.conf 检查工具:test…...

Java学习day1
打开命令提示符(cmd)窗口: 按下winR键,输入cmd 按回车或点击确定,打开cmd窗口 常用cmd命令 盘符名称冒号(D:):盘符切换,示例表示由C盘切换到D盘 dir:查看当前路径下的内…...

ByteTrack多目标跟踪——YOLOX详解
文章目录 1 before train1.1 dataset1.2 model 2 train2.1 Backbone2.2 PAFPN2.3 Head2.3.1 Decoupled Head2.3.2 anchor-free2.3.3 标签分配① 初步筛选② simOTA 2.3.4 Loss计算 项目地址: ByteTrack ByteTrack使用的检测器是YOLOX,是一个目前非常流行…...
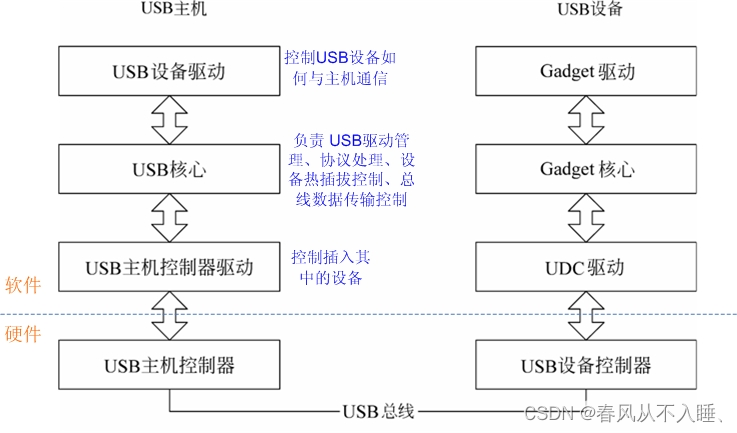
Linux 常见驱动框架
一、V4L2驱动框架 v4l2驱动框架主要对象: (1)video_device:一个字符设备,为用户空间提供设备节点(/dev/videox),提供系统调用的相关操作(open、ioctl…) (2)v4l2_device:…...
)
Oracle函数6—递归查询(start with...connect by、sys_connect_by_path、level)
文章目录 一、准备数据二、基本使用三、level函数四、获取完整的全树路径 一、准备数据 创建表 CREATE TABLE TEST_ORG (ID VARCHAR2(64) NOT NULL PRIMARY KEY,NAME VARCHAR2(200),PARTEN_ID VARCHAR2(64) ); comment on column TEST_ORG.ID is 主键; comment on column TES…...
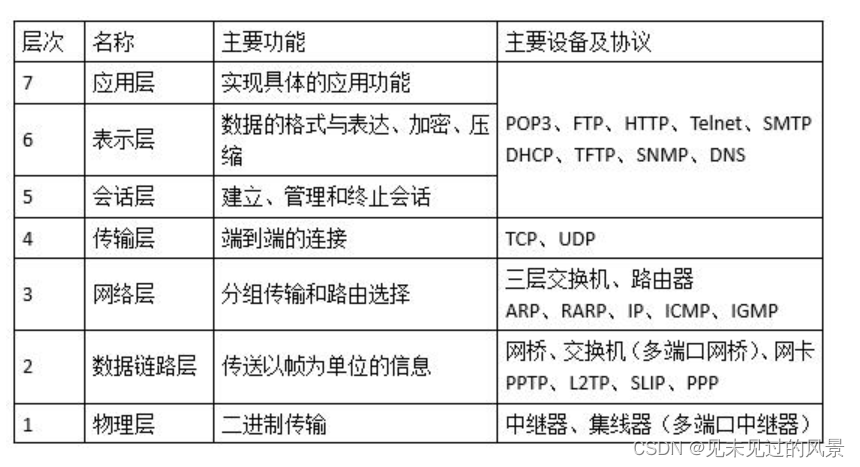
人机交互三原则,网络7层和对应的设备、公钥私钥
人机交互三原则 heo Mandel提出了人机交互的三个黄金原则,它们强调了相似的设计目标,分别是: 简单总结为:控负持面–>空腹吃面 1,用户控制 2,减轻负担 3,保持界面一致 置用户于控制之下&a…...
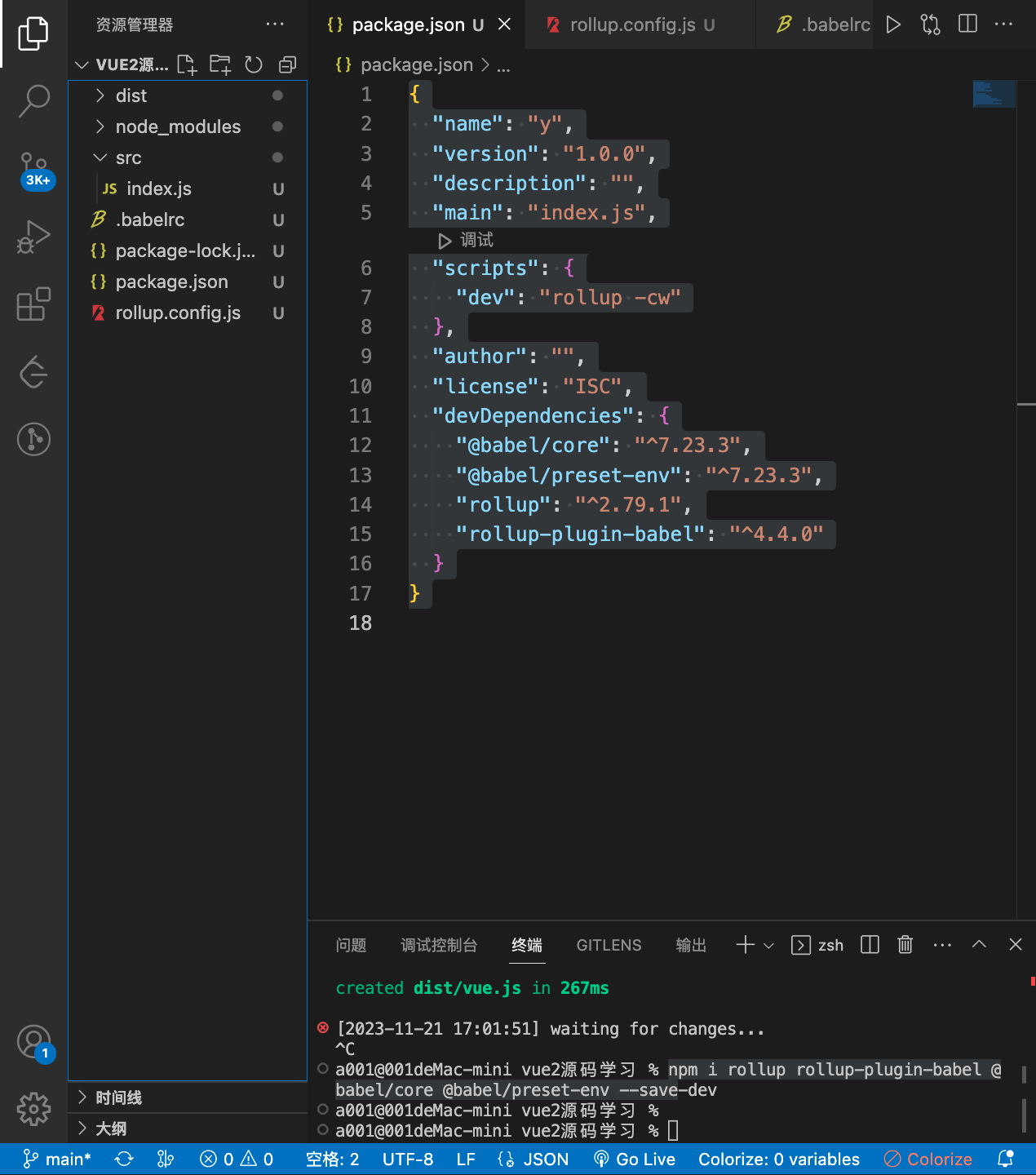
vue2源码学习01配置rollup打包环境
1.下载rollup相关依赖 npm i rollup rollup-plugin-babel babel/core babel/preset-env --save-dev 2.新建rollup.config.js配置打包选项 //rollup可以导出一个对象,作为打包的配置文件 import babel from rollup-plugin-babel export default {input: ./src/ind…...
DP:斐波那契数列模型
创作不易,感谢三连支持 ! 斐波那契数列用于一维探索的单峰函数之中,用于求解最优值的方法。其主要优势为,在第一次迭代的时候求解两个函数值,之后每次迭代只需求解一次 。 一、第N个泰波那契数 . - 力扣(…...
----prmise)
JavaScript高级(十四)----prmise
异步请求的处理方式 回调函数 所谓的回调函数就是函数作为参数的传递,在一个函数内部调用另一个函数,调用的同时可以把内部函数的数据传递出来,他的使用场景就是异步操作,数据需要等待一段时间才能返回的情况下可以使用回调函数…...

28 OpenCV 轮廓周围绘制图形
文章目录 approxPolyDP 轮廓周围绘制矩形boundingRectminAreaRect绘制圆和椭圆示例 approxPolyDP 轮廓周围绘制矩形 approxPolyDP(InputArray curve, OutputArray approxCurve, double epsilon, bool closed)curve:输入点集,二维点向量的集合appro…...

校企合作,助力人才培养——黄冈师范学院-唯众 “实习实训基地”揭牌仪式顺利举行
3月20日上午,黄冈师范学院计算机学院院长何中林、教务处实习科科长雷汝琳以及计算机学院实验室主任肖飞一行三人,莅临唯众进行参观交流。唯众总经理冉柏权、销售总监舒敏以及董事长助理代西凯进行了热情接待。双方就如何更好地结合企业需求与学院教育资源…...

npm audit fix --force
npm audit fix --force是npm的一个命令,用于自动修复包中的安全漏洞。 其中: - npm audit:审查项目中的依赖包,检查是否存在已知的安全漏洞。 - fix:自动安装相关的补丁来修复发现的漏洞。 - --force:强制安装补丁版本,即使出现不兼容也强制更新。 所以npm audit fix --fo…...
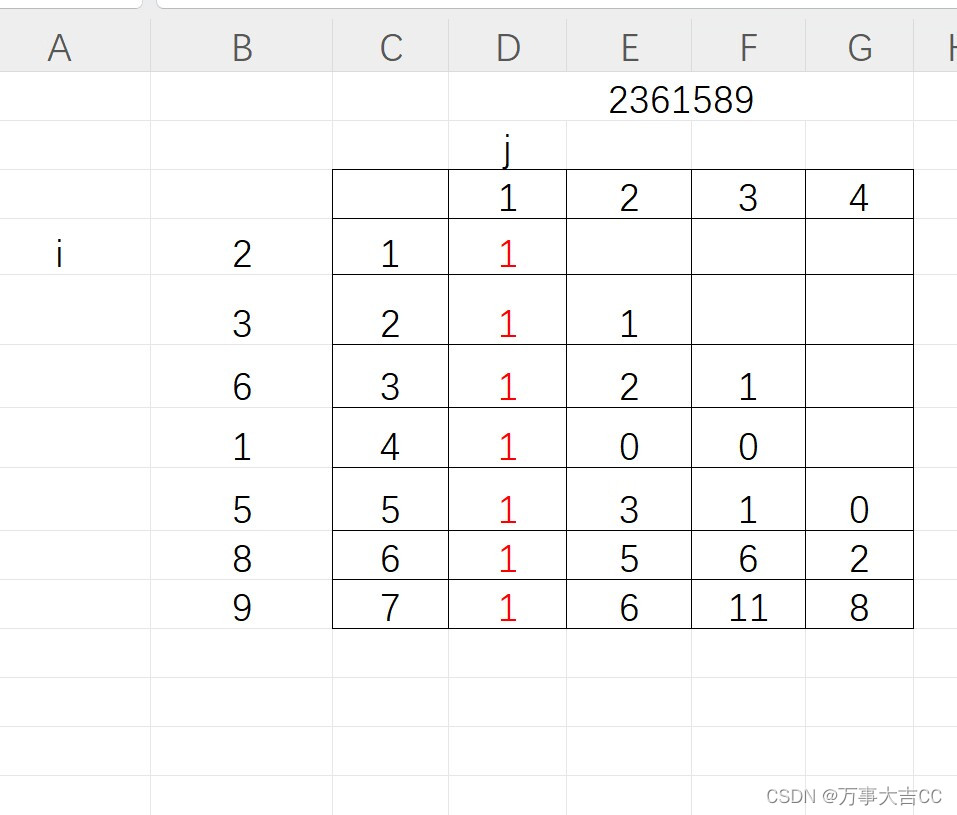
递增四元组
解法: 首先都可以想到dp[i]:第i个元素结尾的递增四元组有dp[i]个 然后发现有一组数据:2,3,6,1,5,8。会出现6结尾和5结尾的递增三元组,也就是未来的决策受过去影响,专业的说就是有后效性。需要强化约束条件࿰…...

蓝桥杯每日一题——棋盘
问题描述 小蓝拥有 n xn 大小的棋盘,一开始棋盘上全都是白子。小蓝进行了 m 次操作,每次操作会将棋盘上某个范围内的所有棋子的颜色取反(也就是白色棋子变为黑色,黑色棋子变为白色)请输出所有操作做完后棋盘上每个棋子的颜色。输入格式 输入的…...
QT6实现创建与操作sqlite数据库及读取实例(一)
一.Qt为SQL数据库提供支持的基本模块(Qt SQL) Qt SQL的API分为不同层: 驱动层 SQL API层 用户接口层 1.驱动层 对于Qt 是基于C来实现的框架,该层主要包括QSqlDriver,QSqlDriverCreator,QSqlDriverCreatorBase,QSqlPlug…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
