【数据结构与算法】(18):树形选择排序:按照锦标赛的思想进行排序
🤡博客主页:Code_文晓
🥰本文专栏:数据结构与算法
😻欢迎关注:感谢大家的点赞评论+关注,祝您学有所成!
✨✨💜💛想要学习更多数据结构与算法点击专栏链接查看💛💜✨✨
在选择类排序中,除了我们以往学习过的简单选择排序和堆排序之外,比较重点的还有树形选择排序,因为这种排序在面试中也偶有出现,所以这节课我们也来讲一讲。
1.1 基本概念与算法描述
树形选择排序又叫锦标赛排序(Tournament Sort),是一种按照锦标赛的思想进行选择排序的方法。属于对简单选择排序的一种改进。
我们尝试描述一下树形选择排序算法:对n个记录的关键字进行两两比较。然后在其中 ⌈⌉ 个较小者中再进行两两比较,如此重复,直到选出最小关键字(按从小到大排序)为止。
以数组 { 16,1,45,23,99,2,18,67,42,10 } 为例,参考图1。

图1从下向上观察,这是第一趟排序,目的是从所有数组中选出值最小的元素。我们尝试描述下具体的操作步骤。
-
开始两两比较,于是元素16和1比较选择1,元素45和23比较选择23,元素99和2比较选择2,18和67比较选择18,42和10比较选择10。
-
现在,选择出的元素1、23、2、18、10又进行两两比较,元素1和23比较选择1,元素2和18比较选择2,元素10没有比较的对象直接被选择。
-
现在,选择出的元素1、2、10又进行两两比较,元素1和2比较选择1,元素10没有比较的对象直接被选择。
-
现在,选择出的元素1、10又进行比较,选择1。最终这个1也是树形结构的树根,找个地方保存本趟排序的最小元素1。
接着,在树叶中把第一趟已经选择出的元素1标记为一个最大值 ∞(这表示元素1不可能在比较中被再次选中了),然后进行第二趟排序,如图2所示。

图2还是从下向上观察,这是第二趟排序,前面挑选出的最小值1已经找了个地方保存,这里直接把1的值修改为一个最大值∞,这样,对节点进行两两比较时,标记为最大值的节点就不可能被选中。第二趟排序需要进行什么比较呢?
-
开始两两比较,元素16和最大值比较,选择元素16。元素45和23、99和2、18和67、42和10就不需要再次比较(因为第一趟排序比较过了)。
-
现在,选择出的元素16和23比较,选择元素16。元素2和18,元素10同样因为第一趟比较过,不需要再次比较。
-
现在,选择出的元素16和2比较,元素10同样因为第一趟比较过,不需要再次比较。
-
现在,选择出的元素2、10进行比较,选择2。最终这个2也是树形结构的树根,找个地方保存本趟排序的最小元素2。
然后继续把第二趟中已经选择出的元素2标记为一个最大值,就可以开始第三趟排序,这里就不赘述了。
所以可以看到,经过一次(第一趟)的完全比较后,从第二趟开始就不再需要完全的两两比较,这样就达到了节省时间提高效率的目的,这就是树形选择排序相较于简单选择排序一个重大的改进之处。但是也应该看到,树形选择排序需要通过构造出二叉树这种树形结构来辅助排序,所以还需要辅助存储空间。
上述图1和图2意在阐述树形选择排序理论,理论上来说树形选择排序并不复杂。但若通过代码实现,则是需要构建一棵完全二叉树来实现对数据排序的。换句话说,图1和图2绘制得比较简单,很多额外的节点并没有绘制出来。
回忆一下二叉树的性质5——具有n(n>0)个节点的完全二叉树的高度为 ⌈⌉ 或者 ⌊
⌋ +1。同时,你也需要知道,含有n个叶子节点的完全二叉树的高度是 ⌈
⌉ +1。以这个理论为指导(为了能够正确编写出代码),绘制一下更详细的树形选择排序示意图。依旧以数组 { 16,1,45,23,99,2,18,67,42,10 } 举例来解释树形选择排序。
-
把该数组中的所有元素都看成是完全二叉树的叶子,根据“含有n个叶子节点的完全二叉树的高度是 ⌈
⌉ +1”,树形选择排序所要创建的这棵完全二叉树高度应该是5。
-
第一趟,两两比较,找到最小值保存到根节点中,如图3所示。

-
接着,沿着根节点向叶子节点找,找到了最小值1所在的叶子节点,把该叶子节点的值从原来保存的1修改为最大值 ∞,如图4所示。

-
接着要开始第二趟比较了,第二趟比较时叶子节点之间不再需要两两比较,只需要16和∞作比较,此时当然是16更小,于是,沿着这个比较路线再前进到树根,就能把当前树中的最小节点找到并保存到根中。如图5所示。

-
接着,沿着根节点向叶子节点找,找到了最小值2所在的叶子节点,把该叶子节点的值从原来保存的2修改为最大值 ∞,如图6所示。

持续上述步骤,就可以把整个数据序列按从小到大的顺序排列好。
1.2 实现代码
下面我给出树形选择排序的实现代码。
#define INT_MAX_MY 2147483647//整型能够保存的最大数值,作为标记使用
//树形选择排序(从小到大)
template<typename T>
void TreeSelSort(T myarray[], int length)
{//ceil是系统函数:ceil(x)函数返回的是大于或等于x的最小整数int treelvl = (int)ceil(log(length) / log(2)) + 1; //5:完全二叉树高度(含有n个叶子节点的完全二叉树的高度是⌈logn⌉ +1)//treelvl高的完全二叉树最多有nodecount个节点,如果有nodecount个节点,此时的完全二叉树其实是满二叉树int nodecount = (int)pow(2, treelvl) - 1; //31:满二叉树是指一棵高度为h,且含有2h-1个节点的二叉树//treelvl-1 高的完全二叉树最多有nodecount2个节点int nodecount2 = (int)pow(2, treelvl - 1) - 1; //15int* pidx = new int[nodecount];//保存节点的下标用的内存//叶子节点保存元素的下标值(就等于保存了元素的值)for (int i = 0; i < length; ++i){pidx[nodecount2 + i] = i; //pidx[15] = 0; pidx[16] = 1....;pidx[24] = 9} //end for//给多余的叶子节点赋予一个最大值作为标记for (int i = nodecount2 + length; i < nodecount; ++i) //i=25~30{pidx[i] = INT_MAX_MY; //pidx[25] = MAX;pidx[26] = MAX; ......pidx[30] = MAX}int tmpnode2 = nodecount2; //15int tmpnode = nodecount; //31//现在要开始给非叶子节点赋值了,非叶子节点下标是[0]~[14]//第一趟排序要给非叶子节点赋值,还要两两进行节点比较,所以要单独处理while (tmpnode2 != 0){//第一次for执行i值分别为:15、17、19、21、23、25、27、29//第二次for执行i值分别为:7,9,11,13//第三次for执行i值分别为:3,5//第四次for执行i值分别为:1for (int i = tmpnode2; i < tmpnode; i += 2){//第一次for这个pidx的下标【(i + 1) / 2 - 1】分别是7,8,9,10,11,12,13,14//第二次for这个pidx的下标【(i + 1) / 2 - 1】分别是3,4,5,6//第三次for这个pidx的下标【(i + 1) / 2 - 1】分别是1,2//第四次for这个pidx的下标【(i + 1) / 2 - 1】分别是0//把两个孩子中小的孩子值给爹if (pidx[i] != INT_MAX_MY && pidx[i + 1] != INT_MAX_MY) //如果pidx[i]和pidx[i+1]都是正常值,那自然是可以比较{if (myarray[pidx[i]] <= myarray[pidx[i + 1]]){pidx[(i + 1) / 2 - 1] = pidx[i];}else{pidx[(i + 1) / 2 - 1] = pidx[i + 1];}}else if( pidx[i] != INT_MAX_MY) //pidx[i]是正常值,因为有上个if在,说明pidx[i + 1]不是正常值{pidx[(i + 1) / 2 - 1] = pidx[i];}else //走到这里,说明pidx[i + 1]是正常值或者是INT_MAX_MY值{pidx[(i + 1) / 2 - 1] = pidx[i + 1];}} //end fortmpnode = tmpnode2; //15,7,3,1tmpnode2 = (tmpnode2 - 1) / 2; //7,3,1,0} //end whileT* ptmparray = new T[length]; //临时保存排好序的数据for (int i = 0; i < length; i++){ptmparray[i] = myarray[pidx[0]]; //将当前最小值赋给ptmparray[i]临时保存int leafidx = 0;//沿树根找最小值结点在叶子中的序号//leafidx = 0,1,3,7,16分别追溯到叶子中的编号for (int j = 1; j < treelvl; j++){if (pidx[2 * leafidx + 1] == pidx[leafidx]){leafidx = 2 * leafidx + 1;}else{leafidx = 2 * leafidx + 2;}} //end for j//此时的leafidx就是完全二叉树叶子节点中的那个最小值的下标pidx[leafidx] = INT_MAX_MY; //leafidx = 16。while (leafidx){//leafidx = 7,3,1,0leafidx = (leafidx + 1)/2 - 1;//序号为leafidx的结点的双亲结点序号if (pidx[2 * leafidx + 1] != INT_MAX_MY && pidx[2 * leafidx + 2] != INT_MAX_MY) //如果pidx[i]和pidx[i+1]都是正常值,那自然是可以比较{if (myarray[ pidx[2 * leafidx + 1]] <= myarray[pidx[2 * leafidx + 2]]){pidx[leafidx] = pidx[2 * leafidx + 1];}else{pidx[leafidx] = pidx[2 * leafidx + 2];}}else if (pidx[2 * leafidx + 1] != INT_MAX_MY){pidx[leafidx] = pidx[2 * leafidx + 1];}else{pidx[leafidx] = pidx[2 * leafidx + 2];}}//end while} //end for i//把数据从ptmparray拷贝回myarrayfor (int i = 0; i < length; i++){myarray[i] = ptmparray[i];} //end for i//释放内存delete[] ptmparray;delete[] pidx;return;
}
在main主函数中,加入测试代码。
int arr[] = {16,1,45,23,99,2,18,67,42,10};
int length = sizeof(arr) / sizeof(arr[0]); //数组中元素个数
TreeSelSort(arr, length);//对数组元素进行树形选择排序
cout <<"树形选择排序结果为:";
for (int i = 0; i < length; ++i)
{cout << arr[i] <<"";
}
cout << endl; //换行代码的执行结果如下:

树形选择排序算法因为含有n个叶子节点的完全二叉树的高度是 ⌈⌉ +1,除了最小关键字外,每次选择其他最小关键字只需要 ⌈
⌉ 次比较,因为还有 n-1 个关键字需要进行这个次数的比较,所以可以认为该算法的时间复杂度是 O(
)。
对于算法的空间复杂度,在上述实现代码中,是需要一些辅助空间帮忙实现排序的(空间换时间),比如存储完全二叉树节点,还可能需要存储其他一些数据比如临时的排好序的数据。当然,也可以用其他办法,而不是必须用临时空间保存排好序的数据,不过总体来看,树形选择排序的空间复杂度为O()。
此外,经过我测试,认为上述算法的实现代码是稳定的。如果你稍微调整一下其实现代码,改为不稳定的也很容易。
1.3 小结
这节课我们一起学习了选择类排序中的树形选择排序。树形选择排序是一种按照锦标赛的思想进行选择排序的方法,属于对简单选择排序的一种改进。它会通过多趟排序来对 n 个记录的关键字进行两两比较,然后在其中 ⌈⌉ 个较小者中再进行两两比较,如此重复,直到选出最小关键字(按从小到大排序)为止。
树形选择排序的每一趟排序都会减少需要两两比较的元素数量,从而达到了节省时间提高效率的目的,这就是树形选择排序相较于简单选择排序一个重大的改进之处。 但是我们也应该看到,树形选择排序需要通过构造出二叉树这种树形结构来辅助排序,所以还需要辅助存储空间。
这篇文章我们也详细解释了树形选择排序的概念,通过多个示意图对该排序的算法进行了详尽的描述,也为你提供了完整的实现代码。最后强调一个细节,树形选择排序算法的时间复杂度是 O(),空间复杂度为 O(
),算法是稳定的。
相关文章:
【数据结构与算法】(18):树形选择排序:按照锦标赛的思想进行排序
🤡博客主页:Code_文晓 🥰本文专栏:数据结构与算法 😻欢迎关注:感谢大家的点赞评论关注,祝您学有所成! ✨✨💜💛想要学习更多数据结构与算法点击专栏链接查看&…...

统计单词数
统计单词数 题目描述 一般的文本编辑器都有查找单词的功能,该功能可以快速定位特定单词在文章中的位置,有的还能统计出特定单词在文章中出现的次数。 现在,请你编程实现这一功能,具体要求是:给定一个单词࿰…...

c++pair的用法
pair简单来说就是可以存储两种类型数据的一个类,其内部是使用模板实现的,所以可以指定其内部的类型。 pair在#include <utility> pair的构造 pair<int, string> p1({ 1,"张三" });pair<int, string> p2;pair<int, str…...

石油炼化5G智能制造工厂数字孪生可视化平台,推进行业数字化转型
石油炼化5G智能制造工厂数字孪生可视化平台,推进行业数字化转型。在石油炼化行业,5G智能制造工厂数字孪生可视化平台的出现,为行业的数字化转型注入了新的活力。石油炼化行业作为传统工业的重要领域,面临着资源紧张、环境压力、安…...

IP代理技术革新:探索数据采集的新路径
引言: 随着全球化进程不断加深,网络数据采集在企业决策和市场分析中扮演着愈发重要的角色。然而,地域限制和IP封锁等问题常常给数据采集工作带来了巨大挑战。亿牛云代理服务凭借其强大的网络覆盖和真实住宅IP资源,成为解决这些问…...
流畅的 Python 第二版(GPT 重译)(一)
前言 计划是这样的:当有人使用你不理解的特性时,直接开枪打死他们。这比学习新东西要容易得多,不久之后,活下来的程序员只会用一个容易理解的、微小的 Python 0.9.6 子集来编写代码 。 Tim Peters,传奇的核心开发者&am…...

Vue+jquery+jquery.maphilight实现图片热区高亮以及点击效果
//鼠标悬浮效果 mounted() {this.setCurrentTask(0); //对于id为mapAll的热区图,设置鼠标放置在上面有一个颜色 fillColor填充颜色 strokeColor边框颜色 strokeWidth边框宽度 fillOpacity 是设置热区填充颜色的不透明度的属性。 alwaysOn:true 保持常量$(function(…...

靠谱!朋友圈一键转发和自动转发好友朋友圈
微信朋友圈在生活和工作中扮演着重要的社交和信息传播角色。尤其是对于一些企业来说,朋友圈是不可或缺的推广渠道。 今天就给大家分享一个能够实现一键转发和自动转发好友朋友圈的工具——微信管理系统,让大家都能有效的管理朋友圈。 1、定时发圈&…...

线性顺序表算法库
list.cpp 具体函数实现 #include <stdio.h> #include "list.h" #include <malloc.h>/************************************************** ①函数名: CreateList 功 能: 用数组构建顺序表 参 数: ①SqList *&L:传入的线性表 ②ElemType a[]:使用…...

java分割等和子集(力扣Leetcode416)
分割等和子集 力扣原题链接 给你一个只包含正整数的非空数组nums。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 示例 1: 输入:nums [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] …...

383. 赎金信
给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。 如果可以,返回 true ;否则返回 false 。 magazine 中的每个字符只能在 ransomNote 中使用一次。 func canConstruct(ransomNote …...

【二】【单片机】有关独立按键的实验
自定义延时函数Delay 分别用Delay.c文件存储Delay函数。用Delay.h声明Delay函数。每次将这两个文件复制到工程中,直接使用。 //Delay.c void Delay(unsigned int xms) //11.0592MHz {while(xms--){unsigned char i, j;i 2;j 199;do{while (--j);}…...

AJAX踩坑指南(知识点补充)
JWT JSON Web Token是目前最为流行的跨域认证解决方案 如何获取:在使用JWT身份验证中,当用户使用其凭据成功登录时,将返回JSON Web Token(令牌) Token本质就是一个包含了信息的字符串 如何获取Token:登录成功之后,服务…...

备战蓝桥杯Day29 - 拼接最大数字问题
问题描述 有n个非负整数,将其按照字符串拼接的方式拼接为一个整数如何拼接可以使得得到的整数最大? 例: 32,94,128,1286,6,71可以拼接除的最大整数为 94716321286128。 问题思路 1.比较两个字符串的第一个数字,数值大的在前面,数值小的在…...
基于springboot的mysql实现读写分离
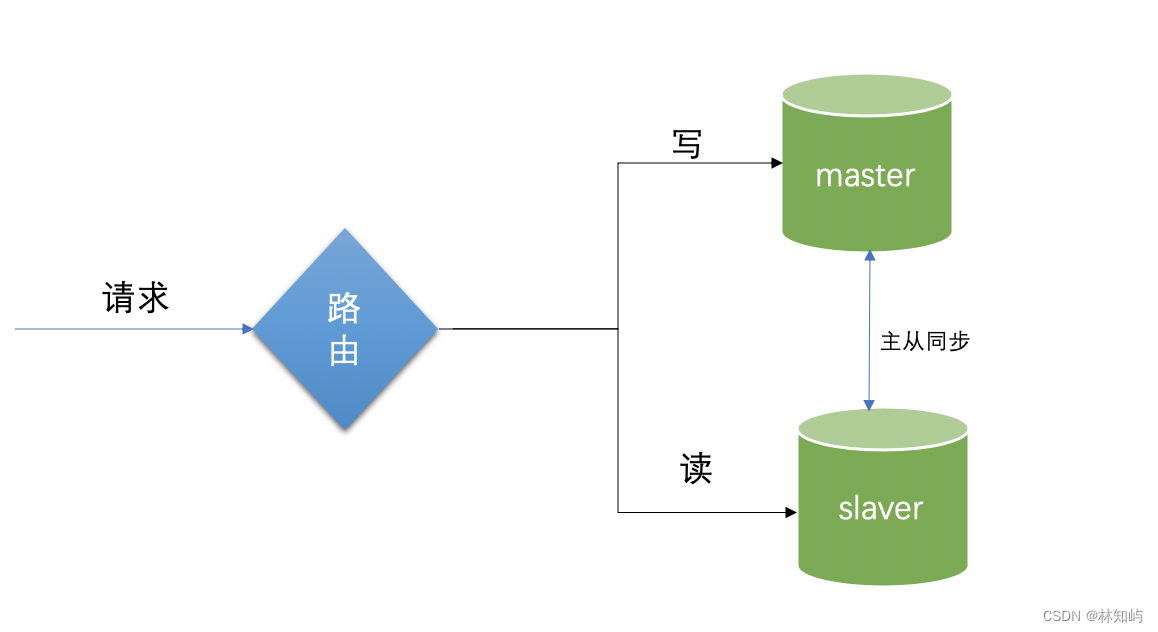
前言: 首先思考一个问题:在高并发的场景中,关于数据库都有哪些优化的手段?常用的有以下的实现方法:读写分离、加缓存、主从架构集群、分库分表等,在互联网应用中,大部分都是读多写少的场景,设置两个库,主库和读库,主库的职能是负责写,从库主要是负责读…...

Python爬虫之Scrapy框架系列(24)——分布式爬虫scrapy_redis完整实战【XXTop250完整爬取】
目录: 每篇前言:1.使用分布式爬取豆瓣电影信息(1)settings.py文件中的配置:(2)spider文件的更改:(3)items.py文件(两个项目一致!&…...
提升效率,稳定可靠:亚信安慧AntDB的企业价值
亚信安慧AntDB分布式数据库凭借平滑扩展、高可用性和低成本三大核心优势,在业界获得了极高的评价和认可。这些优点不仅为AntDB提供了巨大的市场发展潜力,也使其成为众多企业在数据管理上的首选解决方案。 AntDB的平滑扩展特性极大地提升了企业的灵活性和…...

洛谷入门——P1567 统计天数
统计天数 题目描述 炎热的夏日,KC 非常的不爽。他宁可忍受北极的寒冷,也不愿忍受厦门的夏天。最近,他开始研究天气的变化。他希望用研究的结果预测未来的天气。 经历千辛万苦,他收集了连续 N ( 1 ≤ N ≤ 1 0 6 ) N(1 \leq N …...
C++概述
目录 一、C关键字(63个) 二、C几个关键点: 三、C语言缺陷一:命名冲突 四、C新概念:命名空间(namespace) 五、命名空间的嵌套: 六、展开命名空间:(using …...

Linux学习笔记16 - 系统命令
1. Linux 常见系统管理命令 命令含义格式su切换用户su [选项] [用户名]ps显示系统由该用户运行的进程列表ps [选项]top动态显示系统中运行的程序(一般为每隔 5s)topkill输出特定的信号给指定 PID(进程号)的进程,并根据…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
