基于半车悬架的轴距预瞄与轴间预瞄仿真对比
目录
前言
1. 半车悬架模型
2.轴距预瞄(单点预瞄)和轴间预瞄(两点预瞄)原理与仿真分析
2.1轴距预瞄(单点预瞄)
2.1.1预瞄原理
2.2.轴间预瞄(两点预瞄)
2.2.1预瞄原理
2.3仿真分析
3.总结
前言
对于悬架而言,四个车轮实际的输入信息是受到前后延时以及左右相干的,以及我们前车轮走过的路面实际上可以作为后车轮输入的已知信息,或者利用质心与后轮的关系,可以得到已知的后轮激励信息,可以改善悬架的性能指标。
对于目前的文献主要有轴距预瞄(单点预瞄)和轴间预瞄(两点预瞄),本篇将以前后半车(俯仰)悬架进行仿真分析,剖析预瞄的作用和原理所在,这里以半车模型为例:
1. 半车悬架模型
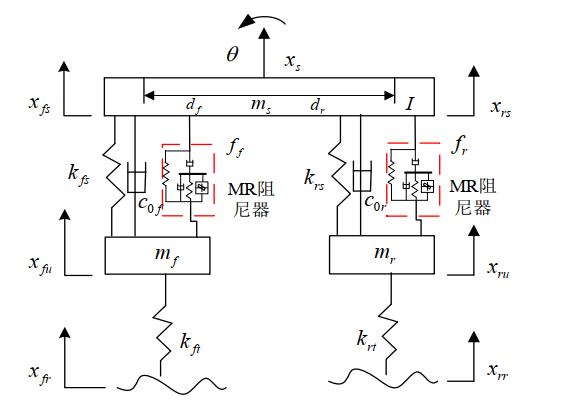
其中, ms、 xs、 xfs、 xrs 分别为簧载质量及其质心、 前端、后端的垂向位移; mf、 xfu 分别为前悬架非簧载质量及其垂向位移; mr、 xru 分别为后悬架非簧载质量及其垂向位移; θ为俯仰角, I 为转动惯量; kfs、 c0f 分别为前悬架的弹簧刚度和不可调阻尼系数; krs、 c0r 分别为后悬架的弹簧刚度和不可调阻尼系数; kft、 krt 分别为前、 后轮胎刚度; ff、 fr 分别为前、后悬架的可调阻尼力; xfr、 xrr 分别为前、 后轮路面激励; df、 dr 分别为前、 后轮到质心的距离。
假设俯仰角很小θ,车身的绝对位移和速度近似为:
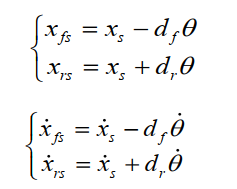
所以前后轮四自由度 1/2 车半主动悬架系统的动力学方程可表示为:
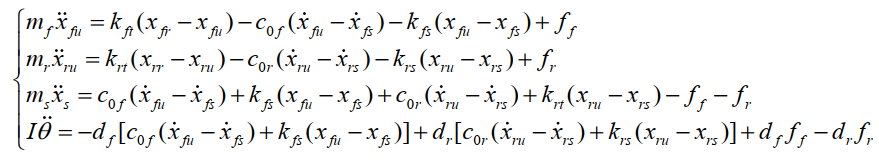
对于其它类型的悬架建模可了解往期链接:
半车(前后、左右)、整车悬架详细推导建模和simulink仿真分析_半车模型的最小实现_Mr. 邹的博客-CSDN博客
2.轴距预瞄(单点预瞄)和轴间预瞄(两点预瞄)原理与仿真分析
2.1轴距预瞄(单点预瞄)
2.1.1预瞄原理
利用传感器的信息可以获得前轮路面激励信息:
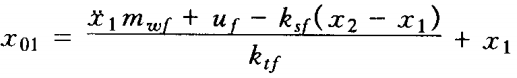
但是对于后轮信息可以通过前轮延时手段获得,虽然传感器传输信息有时间戳,但是认为Δt≈0,所以可以认为x01即为前轮路面激励。
2.2.轴间预瞄(两点预瞄)
2.2.1预瞄原理
同理可以通过传感器信息获得前轮位移信息,后轮的路面位移输入是前轮处延迟以及后轮与前轮轴之间某点(可以理解为质心)处延迟的路面位移信号的某种组合
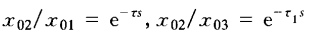
2.3仿真分析
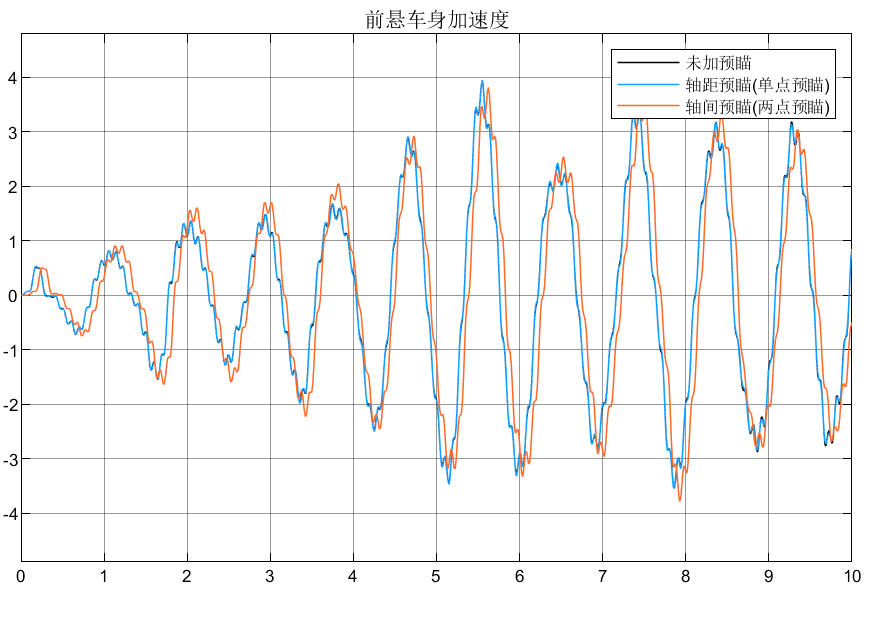
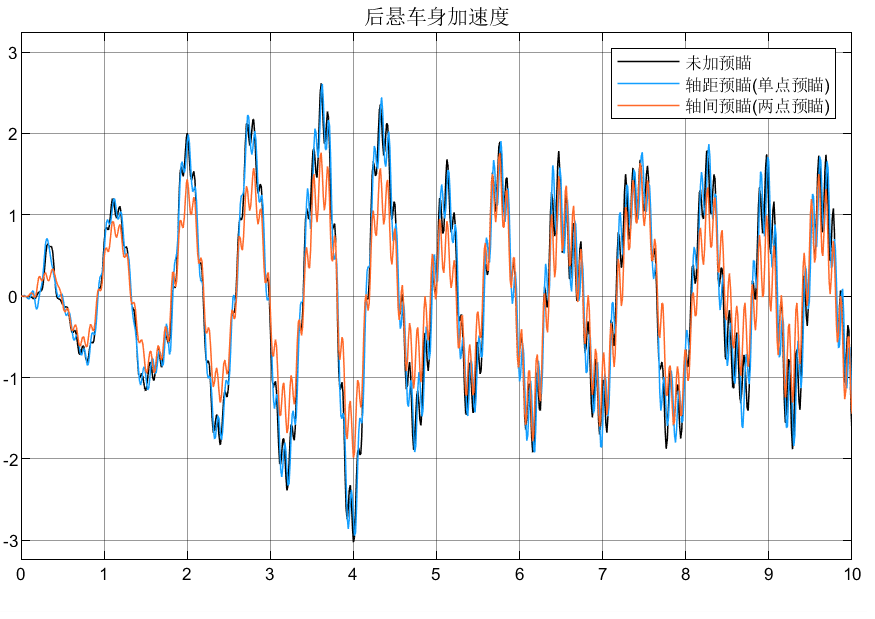
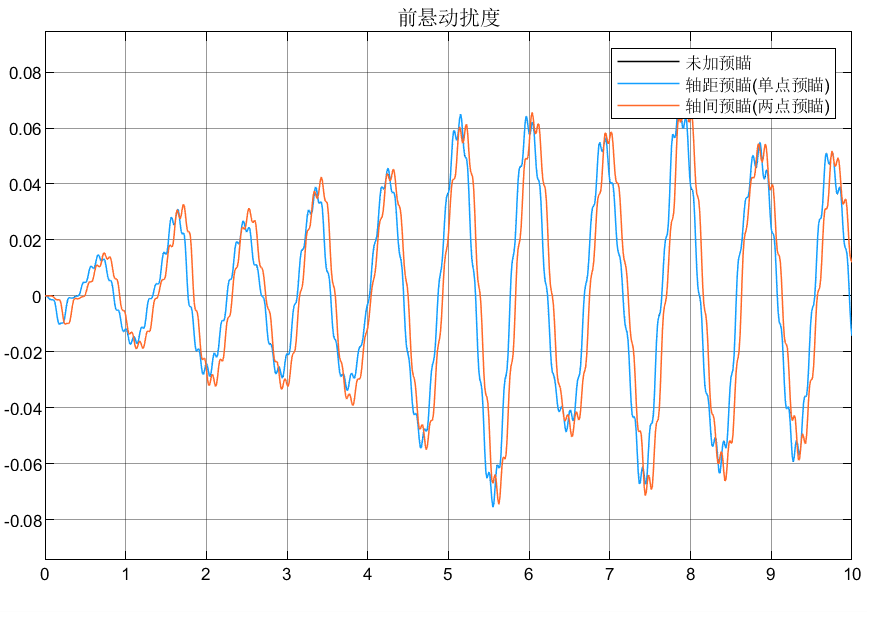
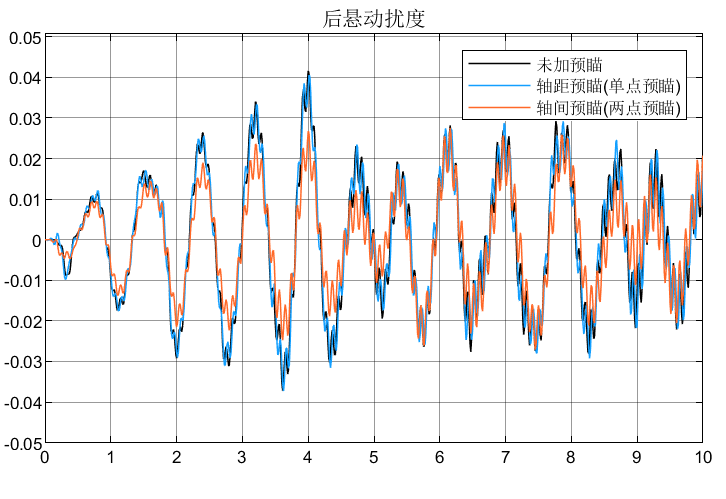
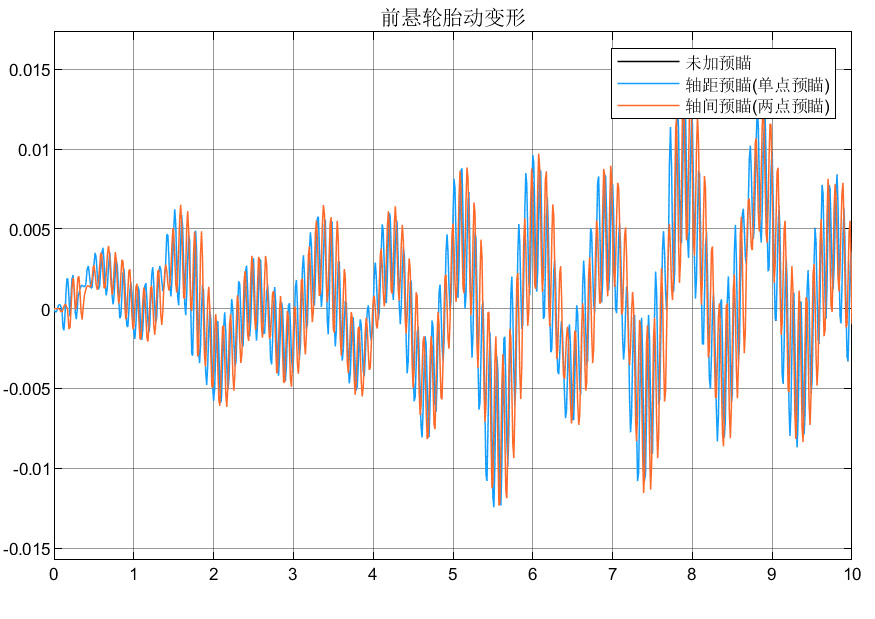
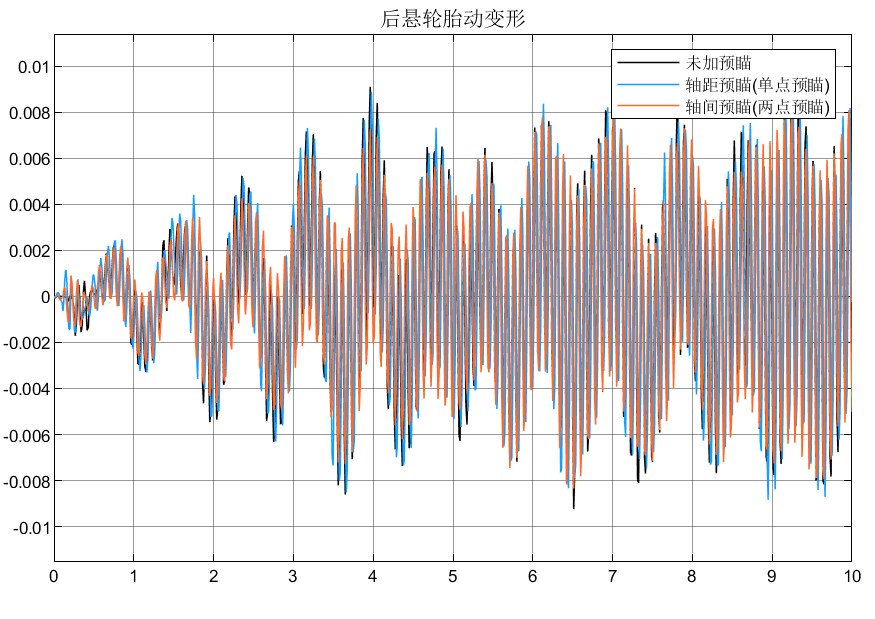
3.总结
①可以看到后悬由于有预瞄,所以相对于前悬的性能指标有所改善;
②轴间预瞄由于可以调节权系数,所以相对于轴距预瞄表现更好。
相关文章:

基于半车悬架的轴距预瞄与轴间预瞄仿真对比
目录 前言 1. 半车悬架模型 2.轴距预瞄(单点预瞄)和轴间预瞄(两点预瞄)原理与仿真分析 2.1轴距预瞄(单点预瞄) 2.1.1预瞄原理 2.2.轴间预瞄(两点预瞄) 2.2.1预瞄原理 2.3仿真分析 3.总结 前言 对于悬架而言,四个车轮实际的输入信息是受到前后延时以及左右相…...

Linux开发 安装JDK8、p4
前面的笔记: Linux 学习笔记1 安装linux详细教程_linux系统 setting_O丶ne丨柒夜的博客-CSDN博客 Linux 学习笔记2 常用命令_O丶ne丨柒夜的博客-CSDN博客 Linux 学习笔记3 权限管理 定时任务 网络配置_O丶ne丨柒夜的博客-CSDN博客 安装配置 安装配置JDK8 Java …...

基于 x86 SoC 的车辆智能驾驶舱和ADAS设计(一)
随着汽车成为软件定义的自动化领域的中心,英特尔致力于提供从汽车到云的可扩展安 全解决方案来加快从高级驾驶员辅助系统(ADAS)到全自动汽车为自动驾驶提供技术支持。 2016 年 3 月,英特尔斥资 153 亿美元收购了以色列高级辅助驾驶系统企业 Mobileye。20…...

类模板函数模板
准备看个项目找实习,边看边学,一看到处都是template 和typename,好几年前学的C都忘记光了,在这里先做个笔记复习一下。template <class T> T abs(T x) {if(x < 0) return -x;return x; } int main() {int x 1;cout <…...

Leetcode DAY 56: 两个字符串的删除操作 and 编辑距离
583. 两个字符串的删除操作 1 、 dp[i][j] 表示 让以word1[i - 1]为结尾的字符串 和 以word2[i - 2]为结尾的字符串 相等需要删除的最少次数 1、dp[i][j] 的 递推需要考虑两种情况: (1)word1[i - 1] word2[j - 1] 相当于不考虑word1[i]和…...

系统检测维护工具Wsycheck使用(18)
实验目的 (1)学习Wsycheck的基本功能; (2)掌握Wsycheck的基本使用方法; 预备知识 windows操作系统的基本知识如:进程、网络、服务和文件等的了解。 Wsycheck是一款强大的系统检测维护工具,进程和…...

111 ok
全部 答对 答错 单选题 1.在与团队一起召开开工会议之后,项目经理分配工作活动,由于与其职能经理分配的任务发生冲突,一位团队成员拒绝开始工作,项目经理首先应该做什么? A请项目发起人帮助与职能经理进行谈判 B签发…...

Python API教程:API入门
什么是API? 一个API,或被称为应用程序接口,是一个服务器为你提供一个接收或发送数据的代码。API通常用来接收数据。 本文就集中焦点在此话题中。 当我们想从一个API中接收数据,我们需要开始请求。请求可以包含整个Web。例如&am…...
SpringMVC学习笔记
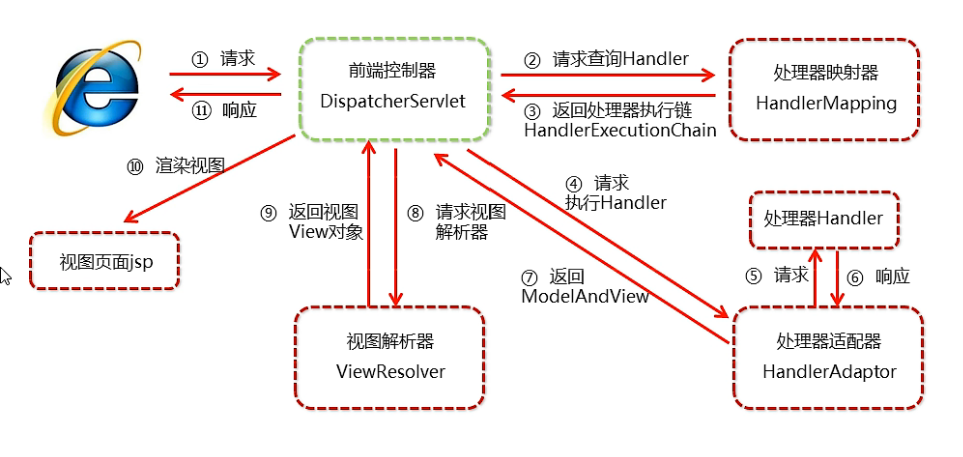
文章目录一、SpringMVC简介1、MVC与三层架构1.1 M1.2 V1.3 C1.4 MVC模式的工作流程1.5 三层架构2、什么是SpringMVC3、SpringMVC的特点二、搭建项目框架1、web项目结构2、创建maven工程,配置pom.xmla>添加web模块b> pom.xml中设置打包方式:warc>…...

Linux学习记录01
文章目录1. Linux基础知识2. Linux常用命令2.1 基础知识2.2 ls命令2.3 cd pwd命令2.4 mkdir2.5 touch、cat、more2.6 cp、mv、rm2.7 通配符、root模式2.8 whicih、find命令2.9 grep、mc、| 管道符2.10 echo、反引号、tail、重定向符2.11 vi、vm文本编辑器1. Linux基础知识 Lin…...
VScode 插件【配置】
写这篇博客的原因: vscode 很久以前的插件,忘记是干什么的了记录 vscode 好用的插件 插件介绍(正文开始) Auto Rename tag 开始/关闭标签内容 同步 Chinese (Simplified) VScode 中文化 CSS Peek 通过 html 代码查找到引用的样式…...
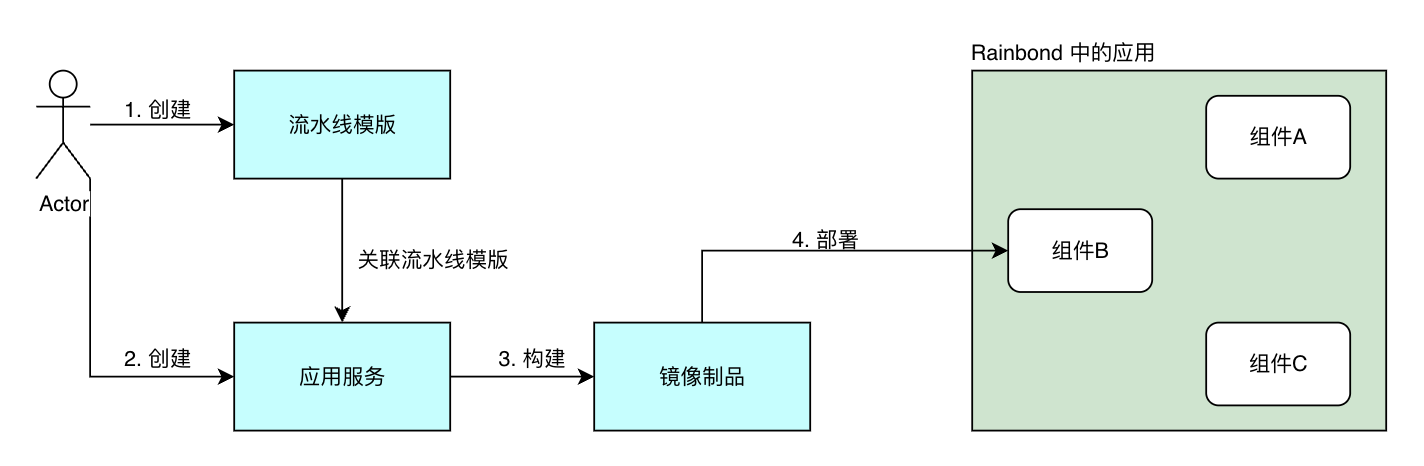
基于 Rainbond 的 Pipeline(流水线)插件
背景 Rainbond 本身具有基于源码构建组件的能力,可以将多种编程语言的代码编译成 Docker 镜像,但是在持续集成的过程中,往往会需要对提交的代码进行静态检查、构建打包以及单元测试。之前由于 Rainbond 并没有 Pipeline 这种可编排的机制&am…...

ASGARD:单细胞导向的药物发现
异质性,或更具体地说,病变组织中的不同的细胞群,是许多复杂疾病治疗失败的主要原因(如癌症、阿尔茨海默症、中风和COVID-19等),也是精准医疗成功的主要障碍。近年来,单细胞技术,特别…...

js-DOM03-事件
事件(Event) - 事件对象 - 当响应函数被调用时,浏览器每次都会将一个事件对象作为实参传递进响应函数中, 这个事件对象中封装了当前事件的相关信息,比如:鼠标的坐标,键盘的按键…...

天梯赛题目练习L1-007--L1-009
1、L1-007 念数字 题目详情 - L1-007 念数字 (pintia.cn) 分数 10 输入一个整数,输出每个数字对应的拼音。当整数为负数时,先输出fu字。十个数字对应的拼音如下: 0: ling 1: yi 2: er 3: san 4: si 5: wu 6: liu 7: qi 8: ba 9: jiu输入格…...

来吧!接受Kotlin 协程--线程池的7个灵魂拷问
前言 之前有分析过协程里的线程池的原理:Kotlin 协程之线程池探索之旅(与Java线程池PK),当时偏重于整体原理,对于细节之处并没有过多的着墨,后来在实际的使用过程中遇到了些问题,也引发了一些思考,故记录之…...

Dynamic Movement Primitives (DMP) 学习
Dynamic Movement Primitives (DMP) 学习 【知乎】Dynamic Movement Primitives介绍及Python实现与UR5机械臂仿真 1. DMP的建模过程 链接:Dynamic Movement Primitives介绍及Python实现与UR5机械臂仿真 - 知乎 (zhihu.com) 沙漏大佬!!&am…...
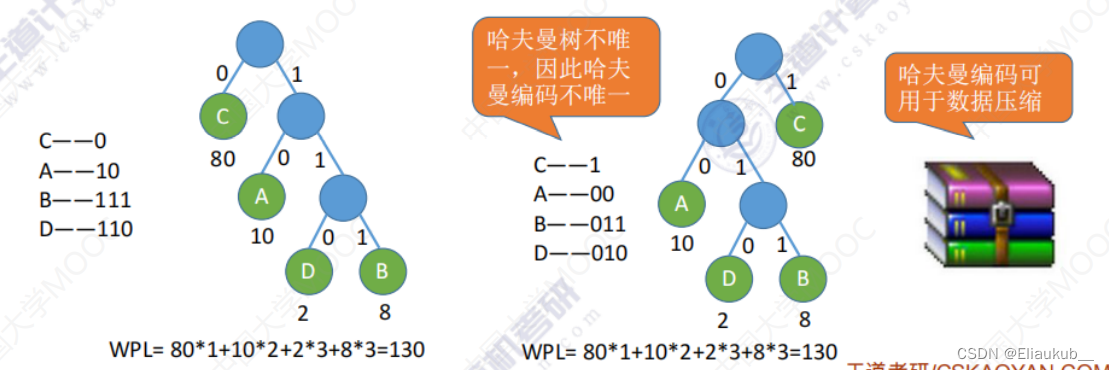
2023王道考研数据结构笔记第五章——树
第五章 树 5.1 树的基本概念 树是n(n≥0)个结点的有限集合,n 0时,称为空树。 空树——结点数为0的树 非空树——①有且仅有一个根节点 ②没有后继的结点称为“叶子结点”(或终端结点) ③有后继的结…...

setState函数是异步的还是同步的?
setState函数是异步的还是同步的? 可能很多同学在看到这个问题的时候,甚至搞不清楚这个问题在问什么。 不要慌,我们看一下下面这个例子,首先我们创建一个类组件,这个类组件中,我们定义了state是一个对象,对象中有一个…...
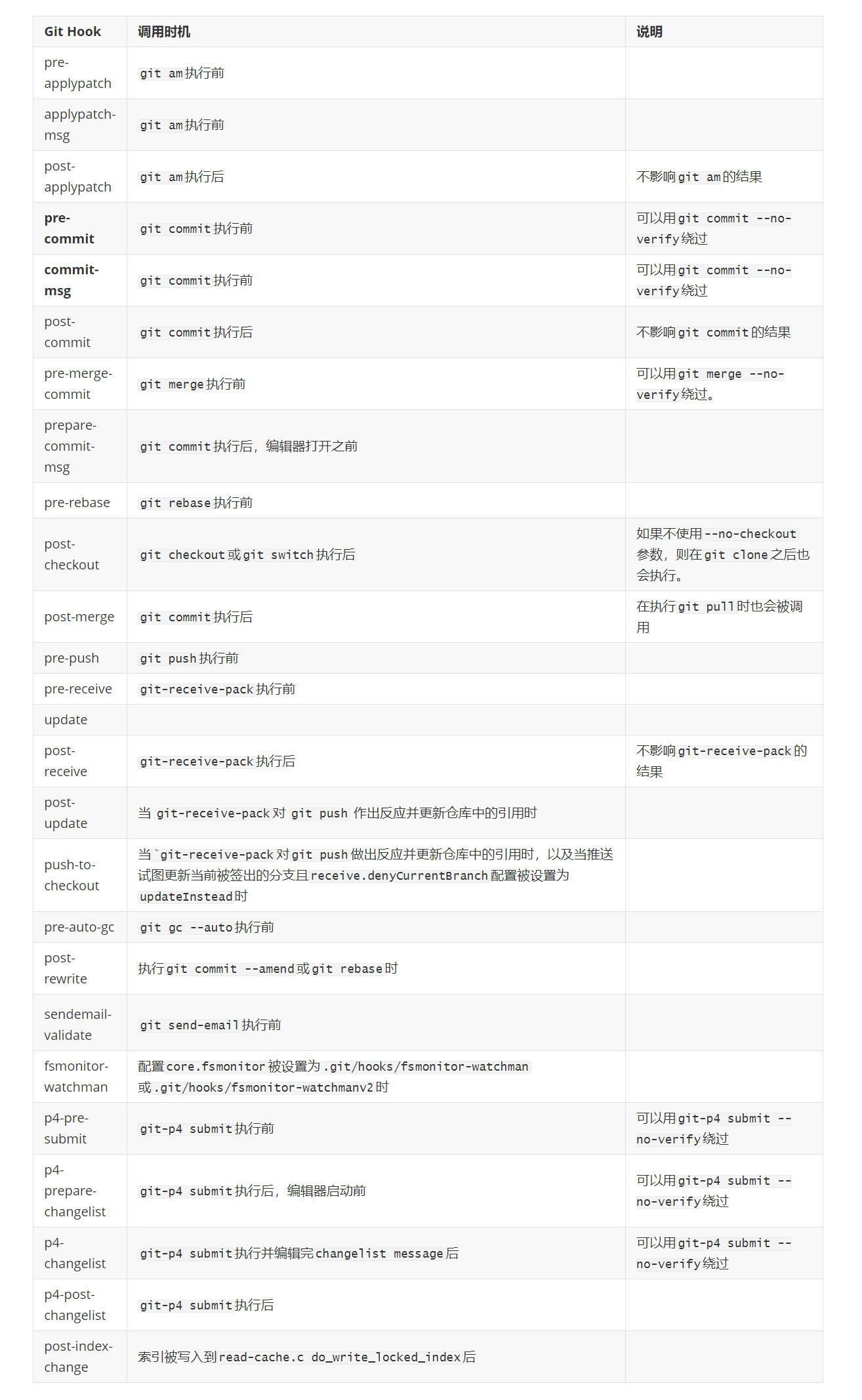
vue3+ts:约定式提交(git husky + gitHooks)
一、背景 Git - githooks Documentation https://github.com/typicode/husky#readme gitHooks: commit-msg_snowli的博客-CSDN博客 之前实践过这个配置,本文在vue3 ts 的项目中,再记录一次。 二、使用 2.1、安装 2.1.1、安装husky pnpm add hus…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
