【并查集专题】【蓝桥杯备考训练】:网络分析、奶酪、合并集合、连通块中点的数量、格子游戏【已更新完成】
目录
1、网络分析(第十一届蓝桥杯省赛第一场C++ A组/B组)
2、奶酪(NOIP2017提高组)
3、合并集合(模板)
4、连通块中点的数量(模板)
5、格子游戏(《信息学奥赛一本通》)
1、网络分析(第十一届蓝桥杯省赛第一场C++ A组/B组)
小明正在做一个网络实验。
他设置了 n 台电脑,称为节点,用于收发和存储数据。
初始时,所有节点都是独立的,不存在任何连接。
小明可以通过网线将两个节点连接起来,连接后两个节点就可以互相通信了。
两个节点如果存在网线连接,称为相邻。
小明有时会测试当时的网络,他会在某个节点发送一条信息,信息会发送到每个相邻的节点,之后这些节点又会转发到自己相邻的节点,直到所有直接或间接相邻的节点都收到了信息。
所有发送和接收的节点都会将信息存储下来。
一条信息只存储一次。
给出小明连接和测试的过程,请计算出每个节点存储信息的大小。
输入格式
输入的第一行包含两个整数 n,m,分别表示节点数量和操作数量。
节点从 1 至 n 编号。
接下来 m 行,每行三个整数,表示一个操作。
- 如果操作为
1 a b,表示将节点 a 和节点 b 通过网线连接起来。当 a = b 时,表示连接了一个自环,对网络没有实质影响。 - 如果操作为
2 p t,表示在节点 p 上发送一条大小为 t 的信息。
输出格式
输出一行,包含 n 个整数,相邻整数之间用一个空格分割,依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
数据范围
1≤n≤10000
1≤m≤1e5
1≤t≤100
输入样例1:
4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1
输出样例1:
13 13 5 3思路:
连接的时候创建一个新的根节点,作为祖先(通过创建新节点,可以实现在之后的dfs中不会将之前的信息加到后连接的计算机上)
依次执行输入的指令,传达的信息都加到根节点上
dfs,把发送的信息全部累加到根节点上
遍历输出根节点的信息(如果对于节点i,p[i]==i则说明这是个根节点,不然说明这个根节点已经其点的子节点了)
代码:
#include<bits/stdc++.h>using namespace std;const int N=2e4+10,M=N<<1;int p[N];int h[M],e[M],ne[M],idx;int add(int a,int b)
{e[idx]=b;//值存到e里(idx是e的编号) ne[idx]=h[a];//d的编号的下一个指向h【a】指向的编号 h[a]=idx++;//h【a】指向b的编号
}int f[N];//存储信息 int n,m;int find(int x)
{if(x!=p[x])p[x]=find(p[x]);return p[x];
}void merge(int a,int b,int &root)
{a=find(a);b=find(b);if(a!=b){p[a]=p[b]=root;add(root,a);add(root,b);root++;}
}void dfs(int son,int father)
{f[son]+=f[father];for(int i=h[son];i!=-1;i=ne[i]){int j=e[i];dfs(j,son);}
}int main()
{memset(h,-1,sizeof h);cin>>n>>m;for(int i=1;i<=n*2;i++){p[i]=i;}int root=n+1; while(m--){int t,a,b;cin>>t;cin>>a>>b;//cout<<"yes";//cout<<m<<endl;if(t==1){merge(a,b,root);}else{a=find(a);f[a]+=b;}//cout<<m<<endl;}//cout<<"yes1";for(int i=n+1;i<root;i++)if(p[i]==i)dfs(i,0);//把每个根节点的值传递到每个计算机上for(int i=1;i<=n;i++)cout<<f[i]<<" ";return 0;
}
/*4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 113 13 5 3*/2、奶酪(NOIP2017提高组)
现有一块大奶酪,它的高度为 h,它的长度和宽度我们可以认为是无限大的,奶酪中间有许多半径相同的球形空洞。
我们可以在这块奶酪中建立空间坐标系,在坐标系中,奶酪的下表面为 z=0,奶酪的上表面为 z=h。
现在,奶酪的下表面有一只小老鼠 Jerry,它知道奶酪中所有空洞的球心所在的坐标。
如果两个空洞相切或是相交,则 Jerry 可以从其中一个空洞跑到另一个空洞,特别地,如果一个空洞与下表面相切或是相交,Jerry 则可以从奶酪下表面跑进空洞;如果一个空洞与上表面相切或是相交,Jerry 则可以从空洞跑到奶酪上表面。
位于奶酪下表面的 Jerry 想知道,在不破坏奶酪的情况下,能否利用已有的空洞跑到奶酪的上表面去?
空间内两点 P1(x1,y1,z1)、P2(x2,y2,z2)的距离公式如下:
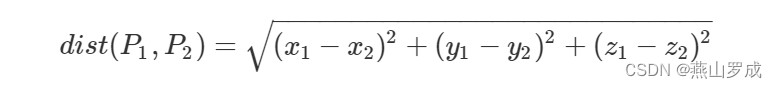
输入格式
每个输入文件包含多组数据。
输入文件的第一行,包含一个正整数 T,代表该输入文件中所含的数据组数。
接下来是 T组数据,每组数据的格式如下:
第一行包含三个正整数 n,h,和 r,两个数之间以一个空格分开,分别代表奶酪中空洞的数量,奶酪的高度和空洞的半径。
接下来的 n 行,每行包含三个整数 x、y、z,两个数之间以一个空格分开,表示空洞球心坐标为 (x,y,z)。
输出格式
输出文件包含 T 行,分别对应 T 组数据的答案,如果在第 i 组数据中,Jerry 能从下表面跑到上表面,则输出 Yes,如果不能,则输出 No。
数据范围
1≤n≤1000
1≤h,r≤1e9
T≤20
坐标的绝对值不超过1e9
输入样例:
3
2 4 1
0 0 1
0 0 3
2 5 1
0 0 1
0 0 4
2 5 2
0 0 2
2 0 4
输出样例:
Yes
No
Yes思路:
多源dfs(推荐)
或者并查集
代码:
多源bfs
#include <bits/stdc++.h>
using namespace std;
int t, n, h, r, f[1010];
double x[1010], y[1010], z[1010];inline double dist(double X1, double X2, double Y1, double Y2, double Z1, double Z2) {return sqrt((X1 - X2) * (X1 - X2) + (Y1 - Y2) * (Y1 - Y2) + (Z1 - Z2) * (Z1 - Z2));
}int main() {scanf("%d", &t);while (t--) {scanf("%d%d%d", &n, &h, &r);for (int i = 1; i <= n; i++) scanf("%lf%lf%lf", &x[i], &y[i], &z[i]), f[i] = 0;queue<int> q; bool ok = 0;for (int i = 1; i <= n; i++) if (z[i] <= r) q.push(i), f[i] = 1;while (q.size()) {int p = q.front(); q.pop();if (ok) break;if (z[p] + r >= h) {ok = 1; puts("Yes"); break;}for (int i = 1; i <= n; i++) {if (f[i]) continue;if (dist(x[p], x[i], y[p], y[i], z[p], z[i]) <= 2 * r) {q.push(i), f[i] = 1;if (z[i] + r >= h) {ok = 1; puts("Yes"); break;}}}}if (!ok) puts("No");}return 0;
}
并查集:
#include <bits/stdc++.h>
using namespace std;
int t, n, h, r;
int t1, s1[1010], t2, s2[1010], fa[1010];
pair<long long, pair<long long, long long> > a[1010];int get(int x) {if (fa[x] != x) fa[x] = get(fa[x]);return fa[x];
}
double dist(double X1, double X2, double Y1, double Y2, double Z1, double Z2) {return sqrt(pow(X1 - X2, 2) + pow(Y1 - Y2, 2) + pow(Z1 - Z2, 2));
}int main() {scanf("%d", &t);while (t--) {scanf("%d%d%d", &n, &h, &r); t1 = 0, t2 = 0;for (int i = 1; i <= n; i++) fa[i] = i;for (int i = 1; i <= n; i++) {scanf("%lld%lld%lld", &a[i].second.first, &a[i].second.second, &a[i].first);if (a[i].first + r >= h) s1[++t1] = i;if (a[i].first - r <= 0) s2[++t2] = i;}if (t1 == 0 || t2 == 0) {puts("No"); continue;}for (int i = 1; i <= n; i++)for (int j = i + 1; j <= n; j++) {if (get(i) == get(j)) continue;double d = dist(a[i].second.first, a[j].second.first, a[i].second.second, a[j].second.second, a[i].first, a[j].first);if (d <= 2 * r) fa[get(i)] = get(j);}int b = 0;for (int i = 1; i <= t1; i++) {if (b) break;for (int j = 1; j <= t2; j++)if (get(s1[i]) == get(s2[j])) {puts("Yes"); b = 1; break;}}if (!b) puts("No");}return 0;
}3、合并集合(模板)
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
M a b,将编号为 a和 b的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 M a b 或 Q a b 中的一种。
输出格式
对于每个询问指令 Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤1e5
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例:
Yes
No
Yes思路:
写好find函数和merge函数
代码:
#include<bits/stdc++.h>using namespace std;const int N=1e5+5;int n,m;int p[N];int find(int x)
{if(x!=p[x])p[x]=find(p[x]);return p[x];
}void merge(int a,int b)
{p[find(a)]=find(b);//a的祖先添加到b的祖先下面
}int main()
{cin>>n>>m;for(int i=1;i<=n;i++)p[i]=i;while(m--){char op;int a,b;cin>>op;cin>>a>>b;if(op=='M'){merge(a,b);}else{if(find(a)==find(b))cout<<"Yes"<<endl;else cout<<"No"<<endl; }}//Yes Noreturn 0;
} 4、连通块中点的数量(模板)
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b之间连一条边,a 和 b 可能相等;Q1 a b,询问点 a 和点 b是否在同一个连通块中,a 和 b 可能相等;Q2 a,询问点 a 所在连通块中点的数量;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。
输出格式
对于每个询问指令 Q1 a b,如果 a和 b 在同一个连通块中,则输出 Yes,否则输出 No。
对于每个询问指令 Q2 a,输出一个整数表示点 a 所在连通块中点的数量
每个结果占一行。
数据范围
1≤n,m≤1e5
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3
思路:
cnt数组统计连通块中点的数量(注意数量全放在祖先节点),合并函数(merge)中进行累加
代码:
#include<bits/stdc++.h>using namespace std;const int N=1e5+10;int n,m;int p[N];
int cnt[N];int find(int x)
{if(x!=p[x])p[x]=find(p[x]);return p[x];
}void merge(int a,int b)
{cnt[find(b)]+=cnt[find(a)];p[find(a)]=find(b);
}int main()
{cin>>n>>m;for(int i=1;i<=n;i++){p[i]=i;cnt[i]=1;}while(m--){char op[5];cin>>op;if(op[0]=='C'){int a,b;cin>>a>>b;if(find(a)==find(b))continue;merge(a,b);}else if(op[1]=='1'){int a,b;cin>>a>>b;if(find(a)==find(b))cout<<"Yes"<<endl;else cout<<"No"<<endl;}else{int t;cin>>t;cout<<cnt[find(t)]<<endl;}}return 0;
}5、格子游戏(《信息学奥赛一本通》)
Alice和Bob玩了一个古老的游戏:首先画一个 n×n的点阵(下图 n=3 )。
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
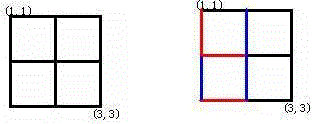
直到围成一个封闭的圈(面积不必为 1)为止,“封圈”的那个人就是赢家。因为棋盘实在是太大了,他们的游戏实在是太长了!
他们甚至在游戏中都不知道谁赢得了游戏。
于是请你写一个程序,帮助他们计算他们是否结束了游戏?
输入格式
输入数据第一行为两个整数 n 和 m。n表示点阵的大小,m 表示一共画了 m 条线。
以后 m 行,每行首先有两个数字 (x,y),代表了画线的起点坐标,接着用空格隔开一个字符,假如字符是 D,则是向下连一条边,如果是 R 就是向右连一条边。
输入数据不会有重复的边且保证正确。
输出格式
输出一行:在第几步的时候结束。
假如 m 步之后也没有结束,则输出一行“draw”。
数据范围
1≤n≤200
1≤m≤24000
输入样例:
3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D
输出样例:
4思路:
注意审题,"轮流在相邻的点之间画上红边和蓝边"表示不存在有孤立的线的情况
可以把每个点进行转换,变成一个独特的数,然后我们就可以把每个点存起来,如果新的两个点转化后,发现有共同祖先那就表示封圈了
代码:
#include<bits/stdc++.h>using namespace std;const int N=4e4+9;//因为二维转化为一维了,所以一维空间必须开N的平方级 (200*200)
int p[N];int find(int x)
{if(x!=p[x])p[x]=find(p[x]);return p[x];
}void merge(int a,int b)
{p[find(a)]=find(b);
}int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n*n;i++)p[i]=i;int cnt=1;for(int i=1;i<=m;i++){int a,b;char c;cin>>a>>b>>c;int p=(a-1)*n+b;//p表示原来的坐标 int q;//q表示另一端(向下或者向右) if(c=='D')q=a*n+b;else q=(a-1)*n+b+1;//cout<<find(p)<<" "<<find(q)<<endl;if(find(p)==find(q)){cout<<i;return 0;}merge(p,q);}cout<<"draw";return 0;
}相关文章:

【并查集专题】【蓝桥杯备考训练】:网络分析、奶酪、合并集合、连通块中点的数量、格子游戏【已更新完成】
目录 1、网络分析(第十一届蓝桥杯省赛第一场C A组/B组) 2、奶酪(NOIP2017提高组) 3、合并集合(模板) 4、连通块中点的数量(模板) 5、格子游戏(《信息学奥赛一本通》…...
数据结构(三)复杂度的深层次剖析
之前发布了数据结构(一),很多同学反响不够清晰,那今天就发一篇对复杂度专题的博客,希望对大家理解复杂度提供一些帮助。 时间复杂度 我们先来一个理解一个复杂度,二分查找的复杂度(之前写过二…...
JavaWeb -- HTTP -- WEB服务器TOMCAT
一.HTTP介绍: HTTP(Hyper Text Protocol) 实际上是一种超文本传输的协议,规定了浏览器跟服务器之间的一些数据传输的规则 例如B/S 对于浏览器的请求,以及相应服务器的响应,都必须依靠这种协议,规范,才能够彼此之间相互 理解 HTTP的协议特点: 1.基于TCP协议: 面向连接 更加安全…...

GitHub与Git命令使用笔记
GitHub与Git命令使用笔记 文章目录 GitHub与Git命令使用笔记上传本地的新项目到github1. 创建新的GitHub仓库2. 初始化本地项目目录3. 将本地仓库关联到GitHub4. 推送本地代码到GitHub上传本地项目到GitHub时发生冲突 将默认分支名称从master改为maingit 把远程项目拉到本地&am…...
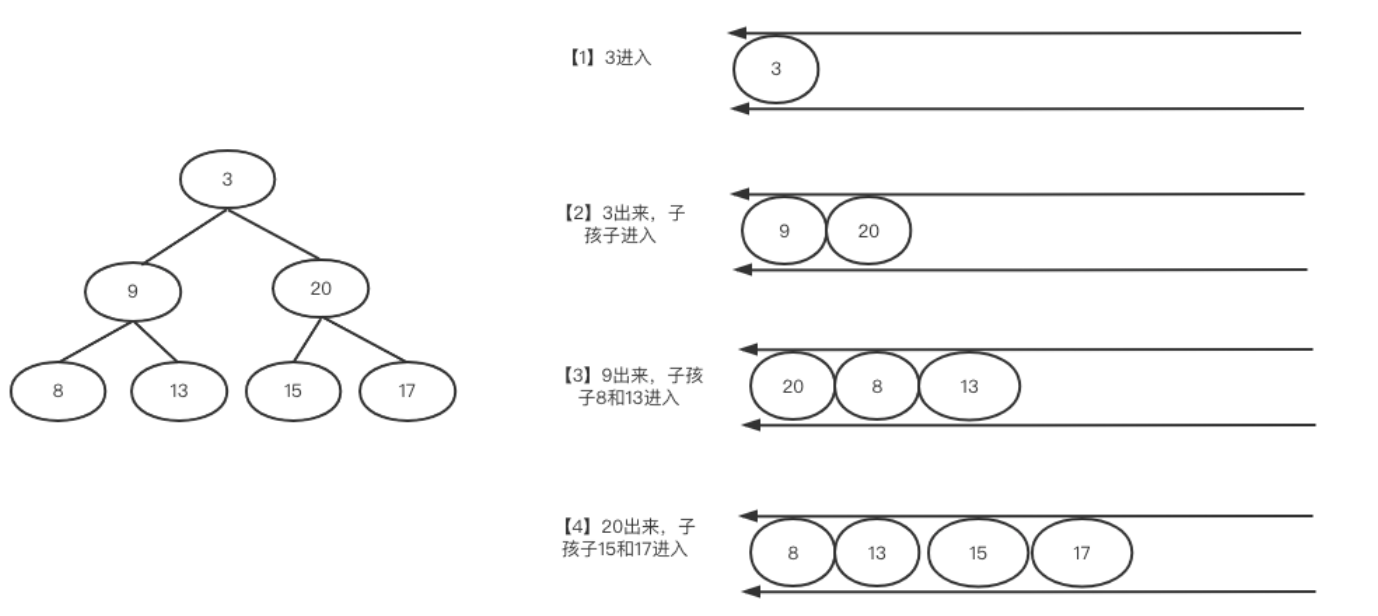
二叉树的层次遍历经典问题-算法通关村
二叉树的层次遍历经典问题-算法通关村 1 层次遍历简介 广度优先在面试里出现的频率非常高,整体属于简单题。广度优先又叫层次遍历,基本过程如下: 层次遍历就是从根节点开始,先访问根节点下面一层全部元素,再访问之后…...

SQLiteC/C++接口详细介绍sqlite3_stmt类(十二)
返回:SQLite—系列文章目录 上一篇:SQLiteC/C接口详细介绍sqlite3_stmt类(十一) 下一篇: SQLiteC/C接口详细介绍sqlite3_stmt类(十三) 48、sqlite3_stmt_isexplain sqlite3_stmt_is…...

大模型时代如何做安全?
现在应该没人怀疑AI时代的到来了吧,在HUB上每天100的新的预训练模型产生,不夸张的说的,现在稍微有点计算机基础的人都可以训练自己的模型了。 说远了,还是说说那些不争气的安全厂商吧。为啥只说安全厂商?因为国内还是…...

新型储能是什么,储能系统解决方案现状及趋势详细说明
新型储能是指新兴的能够存储电能并在需要时释放的储能技术。其中主要包括光伏储能和商业储能。 光伏储能是指通过光伏电池将太阳能转化为电能,并将其存储起来以供后续使用。光伏储能系统一般由太阳能电池板、储能装置和逆变器组成。光伏储能可以将白天产生的电能存…...
)
掌握Go语言:Go语言中的字典魔法,高效数据检索与应用实例解析(18)
在Go语言中,字典通常指的是map类型,它是一种用于存储键值对的数据结构。字典在Go中非常常见,是一种高效的数据结构,用于快速查找和检索数据。 字典的详细使用方法 创建字典 可以使用make函数来创建字典,并指定键值对…...

Flutter-仿携程首页类型切换
效果 唠叨 闲来无事,不小心下载了携程app,还幻想可以去旅游一番,奈何自己运气不好,自从高考时第一次吹空调导致自己拉肚子考试,物理,数学考了一半就交卷,英语2B铅笔除了问题,导致原…...

C语言 自定义类型:结构体
目录 前言 一、结构体类型 1.1 结构体的声明 1.2 结构体变量的创建和初始化 1.3 结构体的特殊声明 1.4 结构体的自引用 二、结构体的对齐 2.1 对齐规则 2.2 内存对齐的原因 2.3 修改默认对齐数 2.4 结构体传参 三、结构体实现位段 3.1 位段的内存分配 3.2 段的跨平…...

计算机网络拓扑结构
目录 <网络拓扑结构概念> <典型的拓扑结构介绍> 第一种,总线型网络拓扑结构 第二种,星型网络拓扑结构 第三种,树型网络拓扑结构 第四种,环型网络拓扑结构 第五种,网状型网络拓扑结构 第六种&#…...

FPGA通过I2C控制AT24C64
文章目录 前言一、代码设计框图二、IIC_drive模块设计2.1、模块接口:2.2、代码功能描述:2.3、IIC协议实现过程: 三、EEPROM_ctrl模块设计3.1、模块接口:3.2、代码功能描述 四、EEPROM_drive模块五、iic_top模块 前言 继上一篇FPG…...
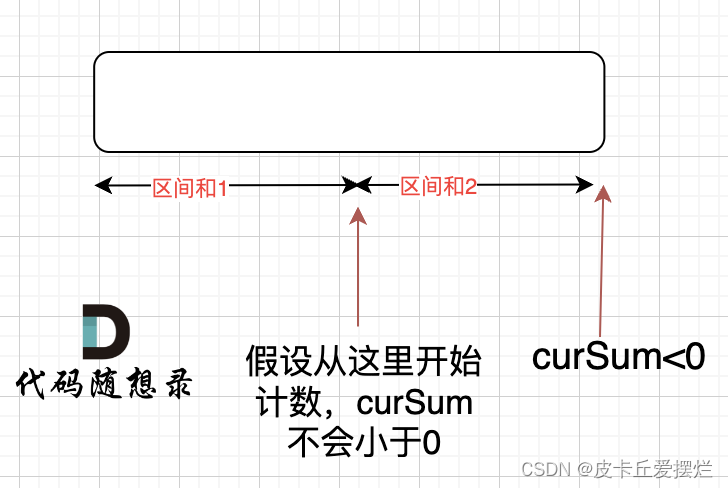
134. 加油站(力扣LeetCode)
文章目录 134. 加油站题目描述暴力枚举(超时)代码一代码二(优化) 贪心算法方法一方法二 134. 加油站 题目描述 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车&…...

XSKY 智能存储,助力“数据要素 X”先进制造
3 月 21-22 日,主题为“突破 智行”的 IMC2024 第七届中国智造数字科技峰会在重庆召开。作为在先进制造领域拥有领先存储解决方案以及众多应用实践的企业,星辰天合受邀参加了此次峰会并荣获大会颁发的“最佳存储解决方案奖”。同时,星辰天合先…...

数据挖掘与分析学习笔记
一、Numpy NumPy(Numerical Python)是一种开源的Python库,专注于数值计算和处理多维数组。它是Python数据科学和机器学习生态系统的基础工具包之一,因为它高效地实现了向量化计算,并提供了对大型多维数组和矩阵的支持…...

linux docker镜像初始化
linux docker镜像初始化 简介 有的镜像内部使用的linux系统特别精简,许多常用命令无法安装,导致排查问题较为困难。 可以使用cat /etc/os-release查看容器使用的linux版本,再进行一些常用操作的初始化。 Debian # 设置镜像源 RUN rm -f /…...

专业140+总分410+南京大学851信号与系统考研经验南大电子信息与通信集成,电通,真题,大纲,参考书。
今年分数出来还是有点小激动,专业851信号与系统140(感谢Jenny老师辅导和全程悉心指导,答疑),总分410,梦想的南大离自己越来越近,马上即将复试,心中慌的一p,闲暇之余&…...

. ./ bash dash source 这五种执行shell脚本方式 区别
实际上,., ./, bash, dash, source 是五种不同的方式来执行 shell 脚本,它们之间有一些区别。 .(点号)或 source 命令:这两个命令是等价的,它们都是 Bash shell 内置的命令。它们用于在当前 shell 环境中执行脚本。当使用 . script.sh 或 source script.sh 命令来执行脚本…...

【React 】React 性能优化的手段有哪些?
1. 是什么 React凭借virtual DOM和diff算法拥有高效的性能,但是某些情况下,性能明显可以进一步提高 在前面文章中,我们了解到类组件通过调用setState方法,就会导致render ,父组件一旦发生render渲染,子组件一定也会执…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
