算法打卡Day14
今日任务:
1)104.二叉树的最大深度
2)559.n叉树的最大深度
3)111.二叉树的最小深度
4)222.完全二叉树的节点个数
104.二叉树的最大深度
题目链接:104. 二叉树的最大深度 - 力扣(LeetCode)
给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
文章讲解:代码随想录 (programmercarl.com)
视频讲解:二叉树的高度和深度有啥区别?究竟用什么遍历顺序?很多录友搞不懂 | LeetCode:104.二叉树的最大深度哔哩哔哩bilibili
思路:
这道题已经在前一篇文章算法打卡day13层序遍历中做过了,如果采用迭代的方法,就用层序遍历,这题比较简单,遍历完所有节点,每遍历一层深度加一即可
今天采用递归(后序遍历)的方法来做,也可以用前序遍历来做(前序遍历涉及到回溯,我还不理解,等后序二刷再来研究),前序遍历求的就是深度,后序遍历求的是高度
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数或者节点数(取决于高度从0开始还是从1开始)
其实弄懂这两个概念,就会发现,在此题求二叉树最大深度中,高度与深度可与转换,当我求二叉树最大深度,也就是最底层叶子节点的深度,也就根节点的高度,所以我们求二叉树最大深度可以转换为,求根节点的高度
求高度我们用后序遍历(左右中),后序遍历是找到叶子节点,然后按左右中每次往上遍历,到中时,需要取左数与右树的最大深度
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution:# 递归(后序)def maxDepth(self, root: [TreeNode]) -> int:return self.getHeight(root)def getHeight(self,node):if not node:return 0leftDepth = self.getHeight(node.left) # 左rightDepth = self.getHeight(node.right) # 右height = 1 + max(leftDepth, rightDepth) # 中return height感想:
这题想清楚了就比较简单,最直截了当的就是层序遍历,递归的方法不好想一点,做之前可能要区分高度与深度,但做完就能跳出深度与高度的概念,后序从下网上,就是从下开始计数,前序从上往下遍历,就是从上开始计数
559.n叉树的最大深度
题目链接:559. N 叉树的最大深度 - 力扣(LeetCode)
给定一个 n 叉树,找到其最大深度。 最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
文章讲解:代码随想录 (programmercarl.com)
思路:
如果采用迭代,层次遍历,这题与上一题一样只是左右节点换成孩子节点了,其他一样
这题如果采用递归的方法,我们也是采用后序遍历
求二叉树深度,我们只需要求出左右树的深度,然后比较,取最大。但是在N叉树中,我们不知道有几个子树,我们需要遍历子树,并用变量记录最大高度,每求一棵树的高度,变与变量比较,将大值重新赋给变量
class Node:def __init__(self, val=None, children=None):self.val = valself.children = childrenclass Solution:def maxDepth(self, root: Node) -> int:return self.getHeight(root)def getHeight(self,node: Node):if not node:return 0height = 0for child in node.children:height = max(height,self.getHeight(child))return height + 1111.二叉树的最小深度
题目链接:111. 二叉树的最小深度 - 力扣(LeetCode)
给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明: 叶子节点是指没有子节点的节点。 这题在02二叉树的层序遍历中做过,采用的层次遍历
文章讲解:代码随想录 (programmercarl.com)
视频讲解:看起来好像做过,一写就错! | LeetCode:111.二叉树的最小深度哔哩哔哩bilibili
思路:
做了前面几题,这题思路比较好像,递归后序遍历,取左右子树的最小高度即可,但这里面有个坑
最小深度是要找根节点到最近叶子节点的距离,注意是叶子节点,也就就是得遇到左右节点均为空才算遇到了叶子节点
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution:def minDepth(self, root: [TreeNode]) -> int:return self.getDepth(root)def getDepth(self, node):# 排除左右节点均为空if not node:return 0leftDepth = self.getDepth(node.left)rightDepth = self.getDepth(node.right)# 注意,叶子节点是需要左右都为空才为叶子节点if node.left == None and node.right:depth = rightDepth + 1elif node.right == None and node.left:depth = leftDepth + 1# 现在还剩左右均不为空的情况else:depth = 1+ min(rightDepth,leftDepth)return depth感想:
以上这两题得递归我写的比较复杂,但是好理解,所以没有放上精简版,如果后面自己熟练了二叉树递归,我在补充上精简版
222.完全二叉树的节点个数
题目链接:222. 完全二叉树的节点个数 - 力扣(LeetCode)
给出一个完全二叉树,求出该树的节点个数。
示例 1:
输入:root = [1,2,3,4,5,6]
输出:6示例 2:
输入:root = []
输出:0
示例 3:输入:root = [1]
输出:1
提示:
树中节点的数目范围是[0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4
题目数据保证输入的树是 完全二叉树
文章讲解:代码随想录 (programmercarl.com)
视频讲解:要理解普通二叉树和完全二叉树的区别! | LeetCode:222.完全二叉树节点的数量哔哩哔哩bilibili
二叉树求节点个数统一思路:
这题有两个思路,不管什么二叉树求节点个数,我们可以用迭代层序遍历,或者递归后序遍历,遍历完计数即可,这样会把每个节点遍历一遍
- 时间复杂度:O(n)
- 空间复杂度:O(log n)
lass TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution:# 一般二叉树求解方法def countNodes(self, root: [TreeNode]) -> int:return self.getNum(root)def getNum(self,node):if not node:return 0leftNum = self.getNum(node.left)rightNum = self.getNum(node.right)totalNode = leftNum + rightNum + 1return totalNode完全二叉树求节点个数思路
对于完全二叉树,我们的遍历过程可以简化,不用遍历所有节点,我们只需要找出二叉树中的满二叉树,满二叉树知道其深度k,可以利用公式2^k-1得到节点个数
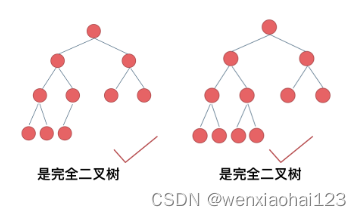
- 完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。
- 满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
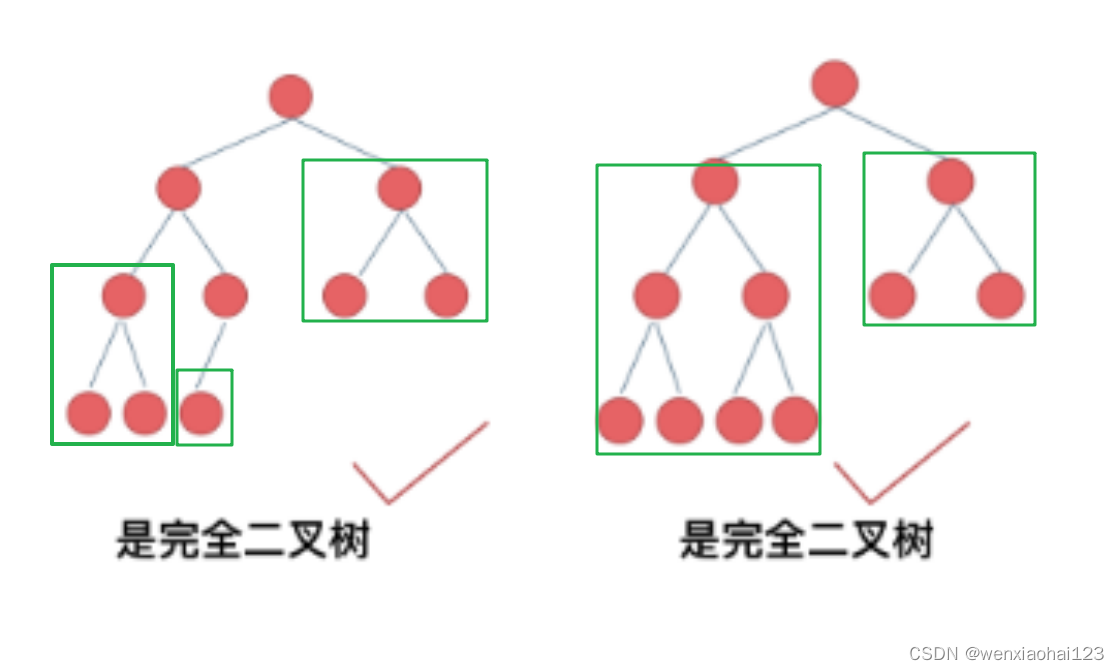
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
如果是满二叉树,直接求节点,如果不是,则需要分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
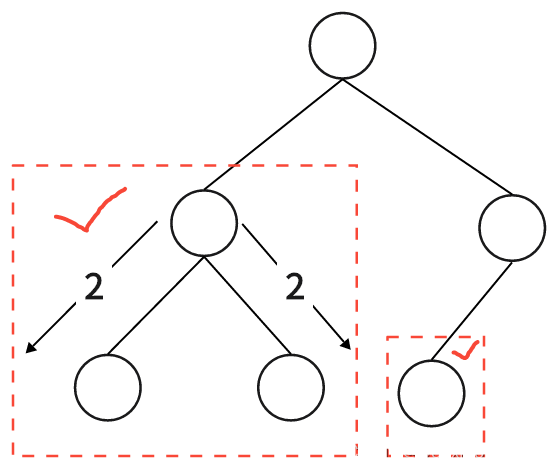
那么如何判断某个树是不是满二叉树
我们只需要判断树的左右最外层是否相等
如,这一种就不等
继续往下找
左边已经找到,计算节点即可,右边继续
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution:# 一般二叉树求解方法def countNodes(self, root: [TreeNode]) -> int:return self.getNum(root)def getNum(self,node):if not node:return 0left = node.leftleftDepth = 1right = node.rightrightDepth = 1# 求左子树深度while left:left = left.leftleftDepth += 1# 求右子树深度while right:right = right.rightrightDepth += 1if leftDepth == rightDepth:return 2**leftDepth - 1return self.getNum(node.left) + self.getNum(node.right) + 1感想:
这题需要自己多画画图,搞清楚完全二叉树概念,下次碰到,不能想到,就用最直接的二叉树统一方法,能够做出来是第一步,优化是第二步
相关文章:
算法打卡Day14
今日任务: 1)104.二叉树的最大深度 2)559.n叉树的最大深度 3)111.二叉树的最小深度 4)222.完全二叉树的节点个数 104.二叉树的最大深度 题目链接:104. 二叉树的最大深度 - 力扣(LeetCode&#…...

Android Kotlin版封装EventBus
文章目录 Android Kotlin版封装EventBus代码封装添加依赖库定义消息类定义常量值定义注解定义工具类 使用在Activity中在Fragment中发送事件 源码下载 Android Kotlin版封装EventBus 代码封装 添加依赖库 implementation("org.greenrobot:eventbus:3.3.1")定义消息…...

VUE父子组件的传参问题
1.父组件向子组件传参 1)这是一个父组件 //这是一个父组件 <div> <port :port-List"portList" ></port> </div> //port 这是子组件的名称export default{components: {},props: {},data() {return{portList:,}},computed: {}…...
四、C#希尔排序算法
简介 希尔排序简单的来说就是一种改进的插入排序算法,它通过将待排序的元素分成若干个子序列,然后对每个子序列进行插入排序,最终逐步缩小子序列的间隔,直到整个序列变得有序。希尔排序的主要思想是通过插入排序的优势࿰…...

华为认证网络工程师的市场需求大吗?
华为认证网络工程师的市场需求非常旺盛,这主要得益于信息技术的快速发展和网络建设的不断扩展。随着云计算、大数据、物联网等新兴技术的普及,企业对于数据通信和网络技术的需求日益增长,为网络工程师提供了广阔的就业空间。 从行业发展趋势来…...
 和nn.ConvTranspose2d())
Pytorch:nn.Upsample() 和nn.ConvTranspose2d()
nn.Upsample 原理 nn.Upsample 是一个在PyTorch中进行上采样(增加数据维度)的层,其通过指定的方法(如nearest邻近插值或linear、bilinear、trilinear线性插值等)来增大tensor的尺寸。这个层可以在二维或三维数据上按…...
百度交易中台之系统对账篇
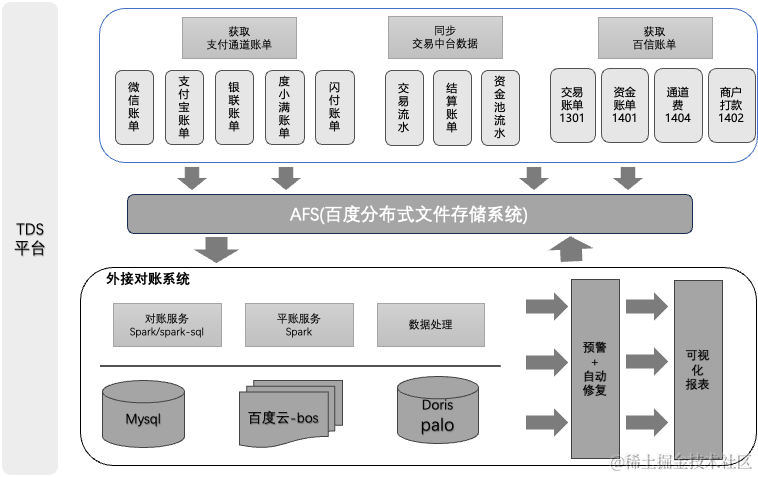
作者 | 天空 导读 introduction 百度交易中台作为集团移动生态战略的基础设施,面向收银交易与清分结算场景,赋能业务、提供高效交易生态搭建。目前支持百度体系内多个产品线,主要包括:度小店、小程序、地图打车、文心一言等。本文…...
Linux 服务升级:MySQL 主从(半同步复制) 平滑升级
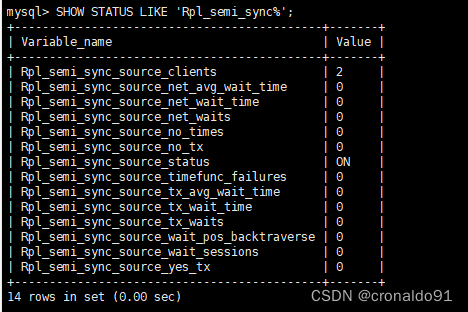
目录 一、实验 1.环境 2.Mysql-shell 检查工具兼容性 3.逻辑备份MySQL数据 4.备份MySQL 数据目录、安装目录、配置文件 5.MySQL 升级 6.master节点 使用systemd管理mysql8 7. slave1 节点升级 8. slave2 节点升级 9.半同步设置 二、问题 1.mysqldump备份报错 2.Inn…...
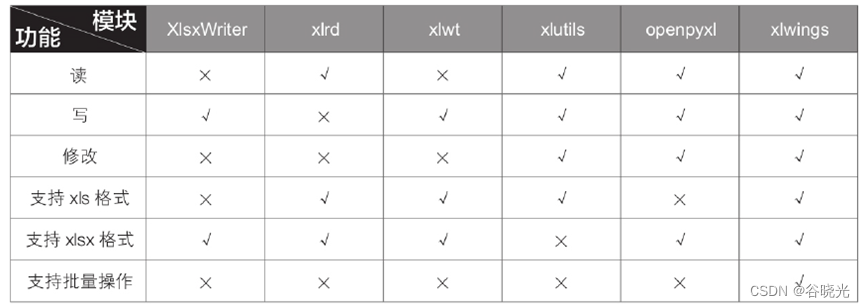
python与excel第一节
python与excel第一节 由于excel在日常办公中大量使用,我们工作中常常会面对高频次或者大量数据的情况。使用python语言可以更加便捷的处理excel。 python与vba的比较 python语法更加简洁,相较于vba冗长复杂的语法,python更加容易学习。 p…...

开发者必备神器 | 全能AI工具助你免费提升开发效率,每日轻松编写代码
全能AI工具助你免费提升开发效率,每日轻松编写代码 前提介绍CodeGeex多语言生成模型支持的编程语言适配多种主流IDE多种IDE插件支持安装VS Code的CodeGeeX插件安装Jetbrains IDEs插件(IntelliJ IDEA,PyCharm)功能实现1. 自动生成和补全代码2. 多语言的代码翻译3. 自动添加注释…...

【RabbitMQ | 第七篇】RabbitMQ实现JSON、Map格式数据的发送与接收
文章目录 7.RabbitMQ实现JSON、Map格式数据的发送与接收7.1消息发送端7.1.1引入依赖7.1.2yml配置7.1.3RabbitMQConfig配置类——(非常重要)(1)创建交换器方法(2)创建队列方法(3)绑定…...
ios symbolicatecrash 符号化crash
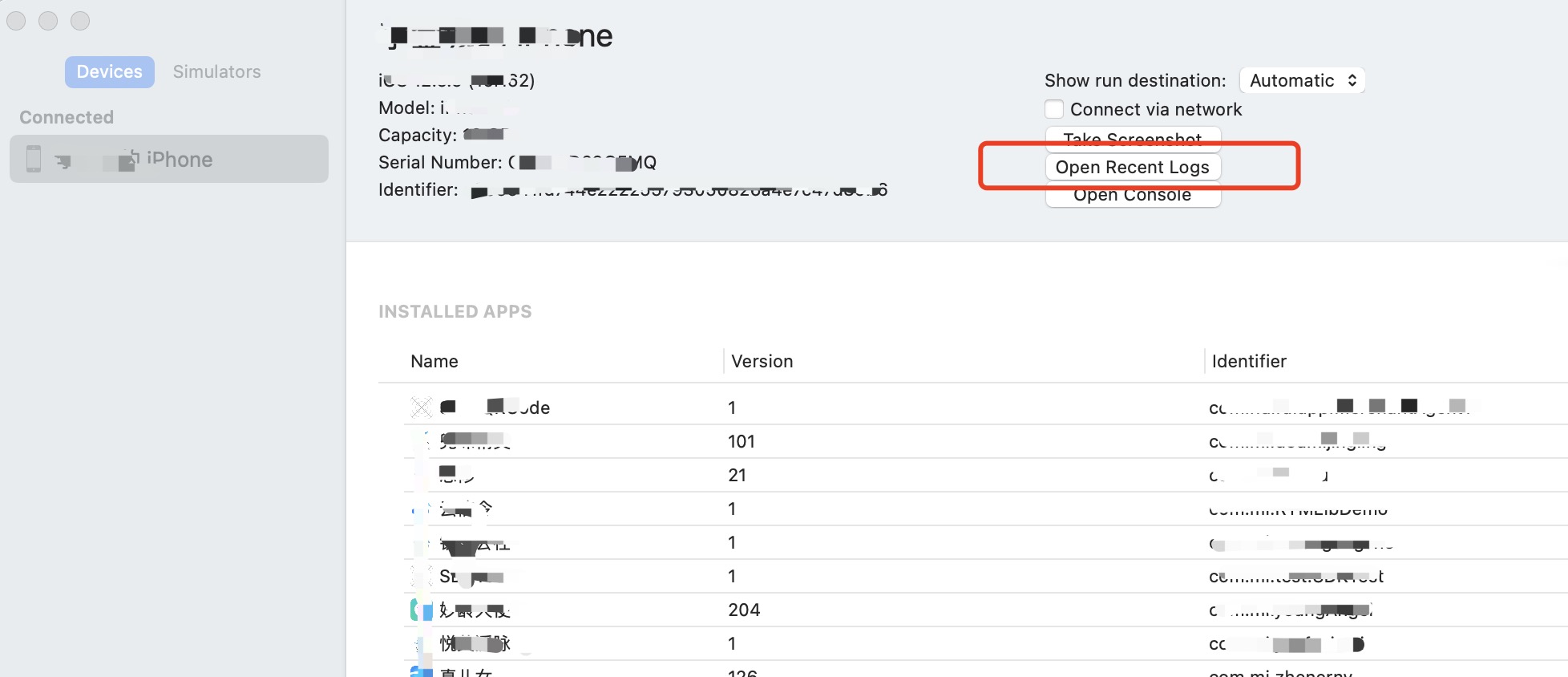
一、准备 1.1 .crash 文件获取 设备连接电脑 打开XCode, 依次 XCode -> Windows -> Device and Simulator -> Open Recent Logs 找到 (对应app名+时间点) -> 右键 Show in Finder 1.2 .dSYM 和 .app 文件获取 .dSYM是十六进制函数地址映射信息的中转文件,调试的…...

Rust 语言的 HashMap
HashMap 在 Rust 中是一个非常常用且强大的数据结构,它允许你存储键值对(key-value pairs),并且能够快速地基于键检索值。 下面是使用 HashMap 的一些基本示例: 首先,你需要在你的文件中引入 HashMap: use std::col…...

【目标检测基础篇】目标检测评价指标:mAP计算的超详细举例分析以及coco数据集标准详解(AP/AP50/APsmall.....))
学习视频: 霹雳吧啦Wz-目标检测mAP计算以及coco评价标准 【目标检测】指标介绍:mAP 1 TP/FP/FN TP(True Positive) : IoU>0.5的检测框数量(同一Ground truth只计算一次)FP(False Positive) : IoU<0.5的检测框(或者是检测到同一个GT的多余检测框的…...

服务器与普通电脑的区别,普通电脑是否可以作为服务器使用
服务器在我们日常应用中非常常见,手机APP、手机游戏、PC游戏、小程序、网站等等都需要部署在服务器上,为我们提供各种计算、应用服务。服务器也是计算机的一种,虽然内部结构相差不大,但是服务器的运行速度更快、负载更高、成本更高…...

长安链Docker Java智能合约引擎的架构、应用与规划
#功能发布 长安链3.0正式版发布了多个重点功能,包括共识算法切换、支持java智能合约引擎、支持后量子密码、web3生态兼容等。我们接下来为大家详细介绍新功能的设计、应用与规划。 在《2022年度长安链开源社区开发者调研报告》中,对Java合约语言支持是开…...
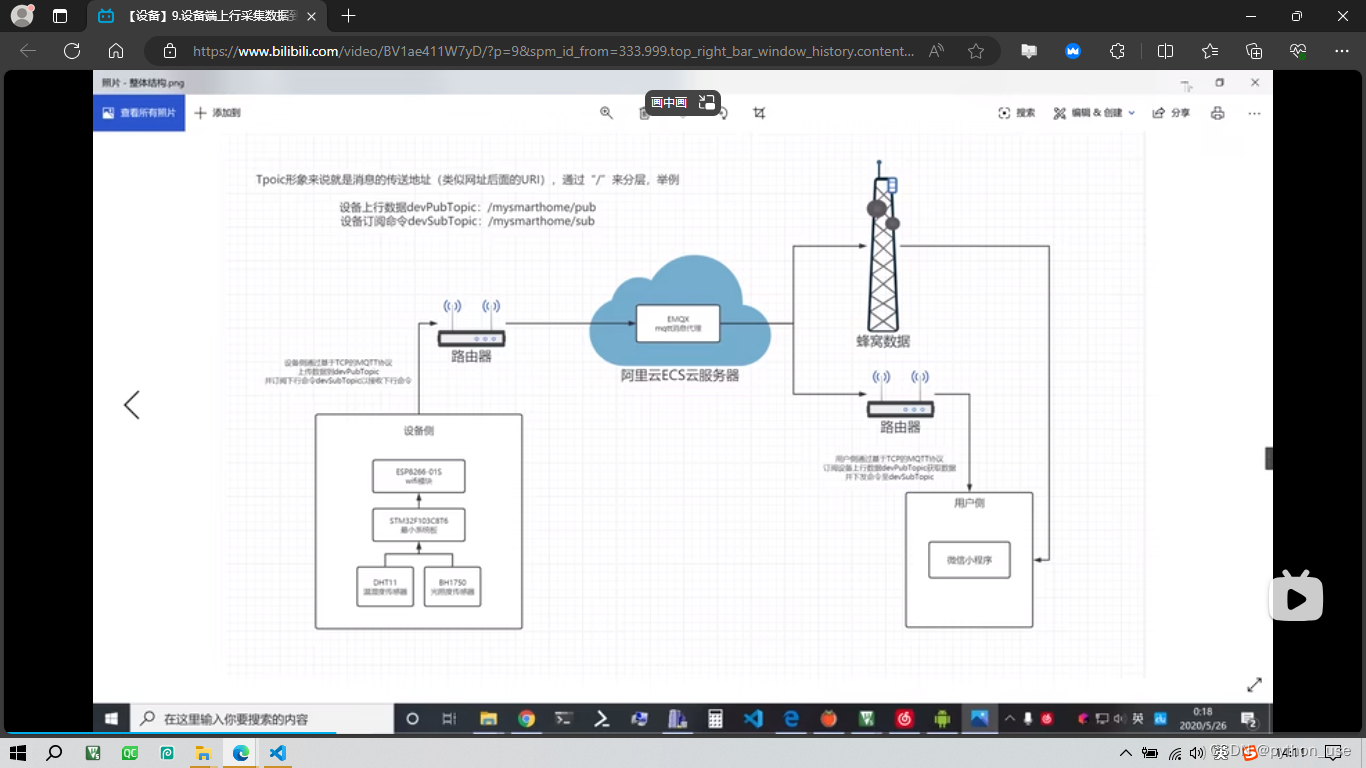
STM32 ESP8266模块的曲折探索
这是本文的配套资料,最终工程请参考 新_ESP8266资料\stm32f103成功移植的项目 【免费】stm32f103c8t6esp8266资料资源-CSDN文库 一、等到了ready 产品参数 我使用的是ai-thinker的esp8266-01s,以下为产品规格书 引脚定义: 依据引脚定义&…...

letcode::根据二叉树创建字符串
根据二叉树创建字符串 题目描述: 给你二叉树的根节点 root ,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。 空节点使用一对空括号对 “()” 表示,转化后需要省略所有不影…...
6个免费的ChatGPT网站
AI 大模型的出现给时代带来了深远的影响: 改变了产业格局:AI 大模型的发展推动了人工智能技术在各行业的广泛应用,改变了传统产业的运作方式,促进了新兴产业的崛起,如智能驾驶、医疗健康、金融科技等。提升了科学研究…...
基础概念)
每天几道面试题|Kafka(一)基础概念
文章目录 什么是 Apache Kafka?它是用来解决什么问题的?Kafka 的主要组件有哪些?它们各自的作用是什么?Kafka 中的生产者和消费者是什么?它们之间的关系是怎样的?Kafka 中的分区是什么?为什么要…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...