牛客小白月赛89补题1(ABCD)(偏难)
评价:
高情商:收获很大 ,让自己进一步认清自己。
低情商:题目难,自己太菜了。
今天还有一些其他事,剩下的题明天再补。
我们从a题开始吧:
A.签到

我们只要看看其中的max与min是否不符合即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,a[1000100],b[1000100],maxx=-1e8,minn=1e8;
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++){maxx=max(maxx,a[i]);minn=min(minn,a[i]);}if(minn-1<1&&maxx+1>m) cout<<"No";else cout<<"Yes";
}B.贪心(喵喵喵)
首先我们可以确定一个结论:
对于负数,我们把全部值都加它,对于正数,我们只要让他加给答案即可。
显然最后留下的一定是原来最大的(粗糙的想一想,每一个数都对答案至少,并且假如一个值一开始1,后来变成负数,我们也把全部值都加它。
这样如果直接模拟n^2,于是我们用sum表示全局要加的值,ans为只有答案要加的,这样子就是n的复杂度了,还是比较妙的。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
long long t,n,a[500010];
bool cmp(int a,int b){return a<b;
}
int main(){cin>>t;while(t--){cin>>n;for(int i=1;i<=n;i++) scanf("%lld",&a[i]);sort(a+1,a+n+1,cmp);long long sum=0,ans=0;for(int i=1;i<=n-1;i++){long long ck=sum+a[i];if(ck>=0) ans+=ck;else{sum+=ck;}}printf("%lld\n",a[n]+sum+ans);}
}C.思维+连通块
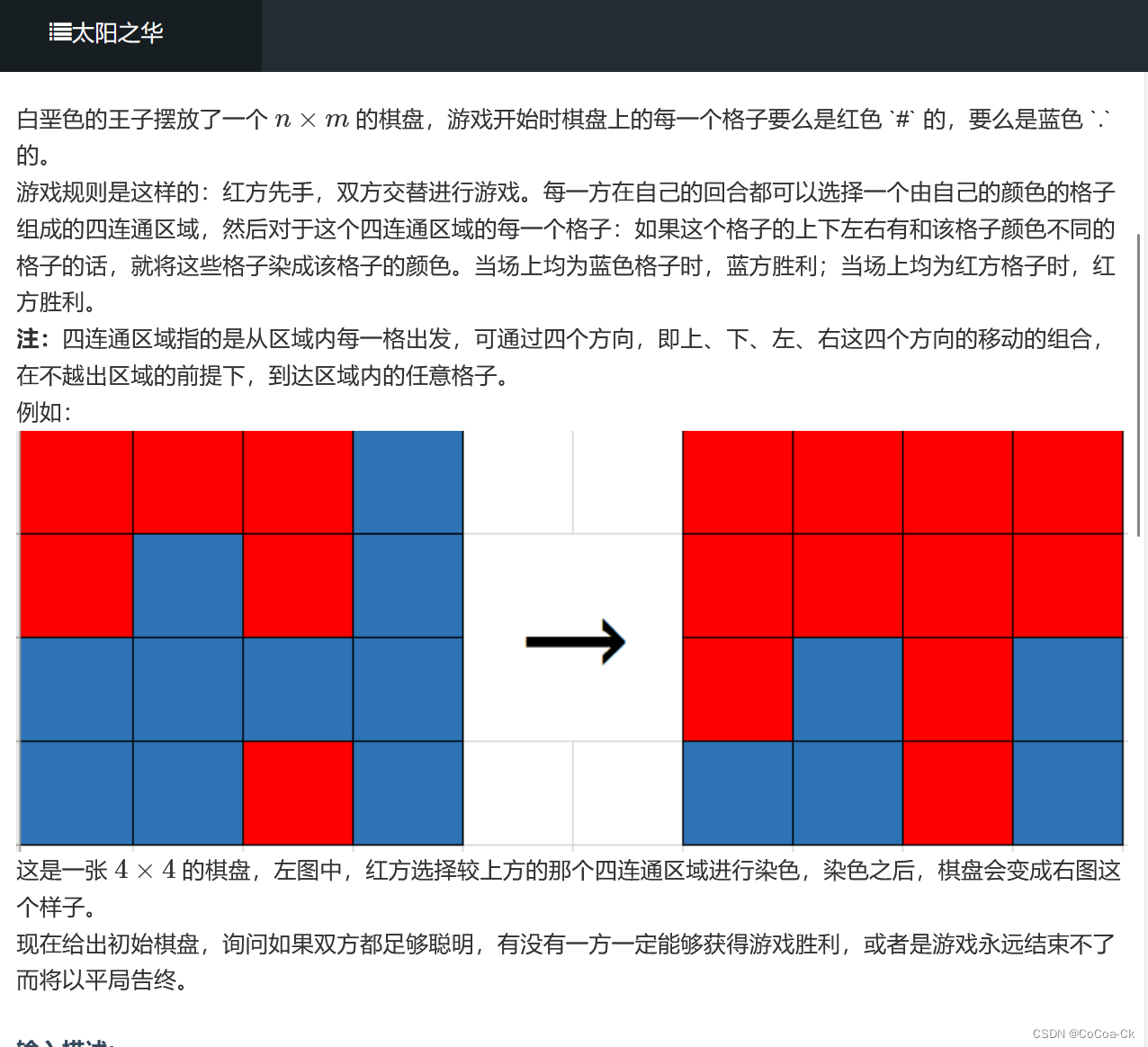
首先,若第一次红可以吃掉蓝,则红胜,否则,蓝一定存在一块,以他扩展,则中心那一个一定不会被吃,因此蓝一定不会输,同理红也一定不会输,那么就是平局。
因此我们可以得到:若开始时红的一个联通块不能吃掉蓝的全部格子就是平局,反之红赢。
这里我们用DFS,并用set记录可以删的数(顺便去重),考虑到x<2000,我们可以在加时直接在x上*2020,这样形成的数是唯一的。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int t,n,m,blue,dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
char a[2010][2010],x;
bool vis[2010][2010];
set<int> s;
void dfs(int x,int y){if(vis[x][y]) return;vis[x][y]=1;for(int i=0;i<4;i++){int xx=x+dir[i][0];int yy=y+dir[i][1];if(xx<1||xx>n||yy<1||yy>m) continue;if(a[xx][yy]=='#') dfs(xx,yy);else s.insert(xx*2020+yy);}
}
int main(){cin>>t;while(t--){blue=0;int win=0;memset(vis,0,sizeof(vis));cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf(" %c",&x);a[i][j]=x;if(x=='.') blue++;}}if(blue==n*m){cout<<"Blue"<<endl;continue;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(vis[i][j]) continue;if(a[i][j]=='#'){s.clear();dfs(i,j);if(s.size()==blue) win=1;}}}if(win) cout<<"Red"<<endl;else cout<<"Draw"<<endl;}
}D.BFS+DP

首先注意到每一个边都为1,显然是考虑BFS,而我们关心的是到x点的每一个距离有几个点。
我们不妨令dp[i][j]表示考虑了dis<=i的所有点放了j个喵点的方案数。
易得状态转移方程dp[i][k]=dp[i-1][k]+dp[i-1][k-1]*c[i](dis==i的个数)。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
long long n,m,q,x,u,v,k,dis[1000100],mod=1e9+7;
vector<int> edge[1000100];
long long dp[5001][5005],cnt[5050];
queue<int> qq;
int main(){cin>>n>>m>>q>>x;for(int i=1;i<=m;i++){scanf("%lld%lld",&u,&v);edge[u].push_back(v);edge[v].push_back(u);}memset(dis,0x3f,sizeof(dis));dis[x]=0;qq.push(x);while(!qq.empty()){int ck=qq.front();qq.pop();for(int i=0;i<edge[ck].size();i++){if(dis[edge[ck][i]]<=5000) continue;dis[edge[ck][i]]=dis[ck]+1;qq.push(edge[ck][i]);}}for(int i=1;i<=n;i++){cnt[dis[i]]++;}dp[0][0]=1;for(int i=1;i<=5000;i++){for(int j=0;j<=5000;j++){dp[i][j]=dp[i-1][j];if(j) dp[i][j]+=dp[i-1][j-1]*cnt[i]%mod;dp[i][j]=dp[i][j]%mod;}}for(int i=1;i<=q;i++){cin>>k;printf("%lld\n",dp[5000][k]);}
}相关文章:

牛客小白月赛89补题1(ABCD)(偏难)
评价: 高情商:收获很大 ,让自己进一步认清自己。 低情商:题目难,自己太菜了。 今天还有一些其他事,剩下的题明天再补。 我们从a题开始吧: A.签到 我们只要看看其中的max与min是否不符合即可…...
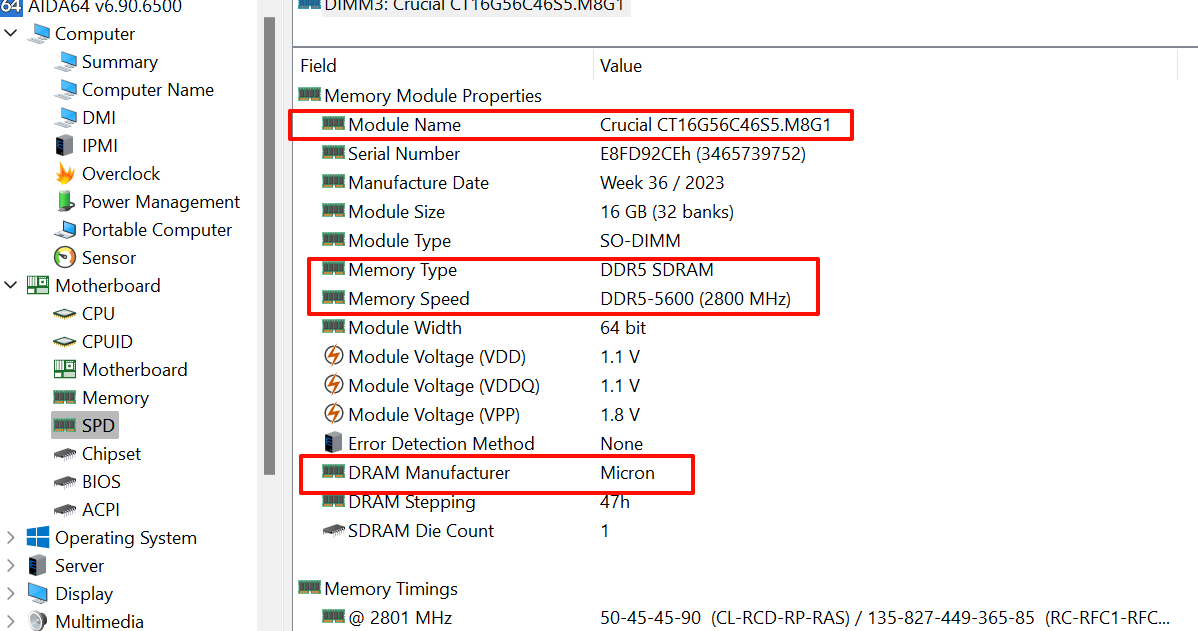
内存条@电脑支持的最大内存@升级内存硬件
文章目录 电脑支持的最大内存规格cpu官网查看支持的规格命令行查看脚本化 DDR内存LPDDR内存内存升级扩展👺插槽检查板载内存SPD内存厂商其他 内存参数👺性能指标使用软件查看更多内存相关的软件工具 电脑支持的最大内存规格 确认电脑最大支持内存大小和频…...

如何了解AI基础概念
1. **在线课程和教程:** - 寻找在线AI课程或教程,例如Coursera、edX、Udemy等平台上的课程。这些课程通常会从基础概念开始介绍,逐步深入。 2. **书籍阅读:** - 阅读与AI相关的书籍,如《Python深度学习》、《机…...
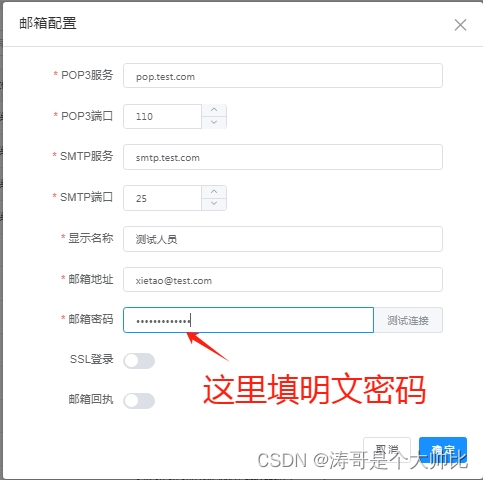
Apache James数据库存储用户信息的密码加密问题
项目场景 Apache James邮件服务器使用数据库来存储用户信息的密码加密问题: 将James的用户改为数据库存储James密码是如何加密验证的 1.将James的用户改为数据库存储 1、修改存储方式 找到james-2.3.2\apps\james\SAR-INF\config.xml 找到<users-store>标…...

大数据分布式事务的深入理解?
在一个大数据系统内部分布式事务无处不在,但凡一个任务分布到多台机器上执行就会涉及到分布式事务的场景,分布式事务一直以来都是分布式系统比较难以解决的问题。 事务的理解,比如你要将账户A转1块钱到账户B中,那么这个行为在执行…...

LeetCode hot100-17
41. 缺失的第一个正数给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 这题要求空间复杂度为O(1),要么定义单个变量,要么原地操作。定义长度为n的数…...

java网络原理(二)------TCP确认应答和超时重传
一Tcp协议 TCP,即Transmission Control Protocol,传输控制协议。人如其名,要对数据的传输进行一个详细的控制。 二.TCP协议段格式 知道了端口号才能进一步确认这个数据报交给了哪一个程序。16为端口号是2字节,范围是0到65535.如…...
机器学习:智能时代的核心引擎
目录 一、什么是机器学习 二、监督学习 三、无监督学习 四、半监督学习 五、强化学习 一、什么是机器学习 机器学习是人工智能的一个分支,它主要基于计算机科学,旨在使计算机系统能够自动地从经验和数据中进行学习并改进,而无需进行明确…...

Docker-Image
Docker Docker 镜像是什么为什么需要镜像镜像命令总览docker imagesdocker tagdocker pulldocker pushdocker rmidocker savedocker loaddocker image inspectdocker historydocker importdocker image prunedocker build Docker 镜像是什么 Docker image 本质上是一个 read-on…...

YOLOv8 如何实现多主干特征融合方式 | GhostNet+ShuffleNet / SwinTransformer+ShuffleNet
文章目录 前言模块添加方法双特征提取例子`GhostNet+ShuffleNet` 双主干结构图代码`Swin+ShuffleNet` 双主干结构图代码参数量与计算量1. 什么是YOLO-Magic框架?2. 如何加入这个框架?3. 加入后如何使用框架?4. GitHub组织是什么?...

工作需求ElementUi组件的使用
加油,新时代打工人! 组件源码 <template><div mouseenter"mousein true" mouseleave"mousein false"><el-input type"text" clearable autocomplete"off" v-model"searchDoc.originName…...
)
自动驾驶轨迹规划之时空语义走廊(一)
欢迎大家关注我的B站: 偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频 (bilibili.com) 目录 1.摘要 2.系统架构 3.MPDM 4.时空语义走廊...
[环境配置].ssh文件夹权限修改方法
问题描述: 通过VSCode中的Remote Explorer或者通过CMD等命令行窗口连接远程机器时,会因为提示 "Bad owner or permissions on C:\\Users\\xxx/.ssh/config"而导致失败,最终呈现在VSCode中的效果是,弹窗提示"Could…...

LeetCode刷题【树状数组、并查集、二叉树】
目录 树状数组307. 区域和检索 - 数组可修改406. 根据身高重建队列673. 最长递增子序列的个数1409. 查询带键的排列 并查集128. 最长连续序列130. 被围绕的区域 二叉树94. 二叉树的中序遍历104. 二叉树的最大深度101. 对称二叉树543. 二叉树的直径108. 将有序数组转换为二叉搜索…...
使用POI以OLE对象的形式向excel中插入附件(pdf为例)
前言: 最近在使用easyExcel操作excel文件时,一直想找到一个方法可以往excel中填充附件,但是目前只发现POI可以插入附件,于是将方法记录如下: 实现: 这个方法主要是使用 Apache POI 的 HSSFWorkbook 类来…...
——SBP的初始设置和脚本编译)
Unity构建详解(2)——SBP的初始设置和脚本编译
【SwitchToBuildPlatform】 核心逻辑如下 EditorUserBuildSettings.SwitchActiveBuildTarget(m_Parameters.Group, m_Parameters.Target); 直接调用切换平台的接口,一般来说,这个步骤不会执行,我们打包时肯定会事先将平台切换好的 【Rebu…...
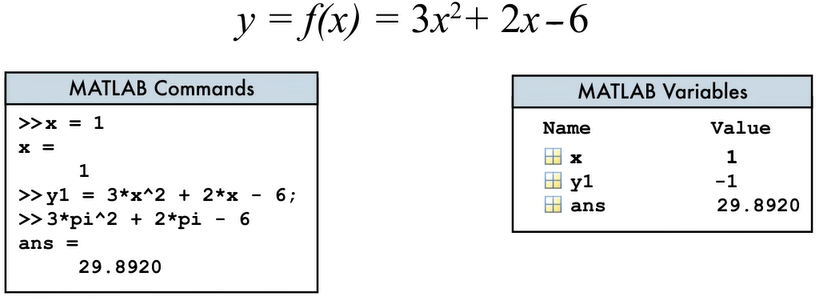
Matlab使用教程(持续更新)
1. Matlab Matlab被广泛的应用在数据分析,汽车仿真,机器人以及医学研究等众多方面。 它可以帮助我们理解研究复杂的系统。 在60年代和70年代,计算机使得科学家和工程师完成了以前不可能进行的计算;但是需要懂得计算机编程。 C…...

管理能力学习笔记一:角色转身
管理能力学习是为了解决角色转身后面临的更多更复杂的的问题。初晋管理层,需要转变工作习惯,学会分配时间。 角色转身 建立“授权”意识 通过匹配工作内容与下属员工能力,分配工作,避免陷入下属能力不足 -> 不愿授权 -> 下…...

Redis面试题 概要
文章目录 Redis面试题 概要缓存穿透布隆过滤器缓存击穿缓存雪崩数据同步数据持久化数据过期策略Redis的数据淘汰策略Redis + Lau 限流Redis面试题 概要 Redis是一个基于 C 语言开发的开源 NoSQL 数据库,Redis 的数据是保存在内存中的(内存数据库,支持持久化),因此读写速度…...

原型,模板,策略,适配器模式
原型模式 原型模式(创建型模式),核心思想就是:基于一个已有的对象复制一个对象出来,通过复制来减少对象的直接创建的成本。 总结一下,原型模式的两种方法,浅拷贝只会复制对象里面的基本数据类型…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
