LeetCode刷题【树状数组、并查集、二叉树】
目录
- 树状数组
- 307. 区域和检索 - 数组可修改
- 406. 根据身高重建队列
- 673. 最长递增子序列的个数
- 1409. 查询带键的排列
- 并查集
- 128. 最长连续序列
- 130. 被围绕的区域
- 二叉树
- 94. 二叉树的中序遍历
- 104. 二叉树的最大深度
- 101. 对称二叉树
- 543. 二叉树的直径
- 108. 将有序数组转换为二叉搜索树
树状数组
307. 区域和检索 - 数组可修改
给你一个数组 nums ,请你完成两类查询。
其中一类查询要求 更新 数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间( 包含 )的nums元素的 和 ,其中 left <= right
实现 NumArray 类:
NumArray(int[] nums) 用整数数组 nums 初始化对象
void update(int index, int val) 将 nums[index] 的值 更新 为 val
int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间( 包含 )的nums元素的 和 (即,nums[left] + nums[left + 1], ..., nums[right])
class NumArray {
private:vector<int> tree;vector<int> &nums;int lowBit(int x){return x & -x;}void add(int index, int val){while(index < tree.size()){tree[index] += val;index += lowBit(index);}}int prefixSum(int index){int sum = 0;while(index > 0){sum += tree[index];index -= lowBit(index);}return sum;}public:NumArray(vector<int>& nums) : tree(nums.size() + 1), nums(nums) {for(int i = 0; i < nums.size(); i++){add(i + 1, nums[i]);}}void update(int index, int val) {add(index + 1, val - nums[index]);nums[index] = val;}int sumRange(int left, int right) {return prefixSum(right + 1) - prefixSum(left);}
};
406. 根据身高重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
class Solution {
public:vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {sort(people.begin(), people.end(), [](const vector<int>& u, const vector<int>& v){return u[0] < v[0] || (u[0] == v[0] && u[1] > v[1]);});int n = people.size();vector<vector<int>> ans(n);for(vector<int>& person : people){int spaces = person[1] + 1;for(int i = 0; i < n; i++){if(ans[i].empty()){spaces--;if(!spaces){ans[i] = person;break;}}}}return ans;}
};
673. 最长递增子序列的个数
给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。
注意 这个数列必须是 严格 递增的。
示例 1:
输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n, 1), cnt(n, 1);int maxs = 1;int count = 0;for(int i = 0; i < n; i++){for(int j = 0; j < i; j++){if(nums[j] < nums[i]){if(dp[i] < dp[j] + 1){dp[i] = dp[j] + 1;cnt[i] = cnt[j];}else if(dp[i] == dp[j] + 1){cnt[i] += cnt[j];}}}if(dp[i] > maxs){maxs = dp[i];count = cnt[i];}else if(dp[i] == maxs){count += cnt[i];}}return count;}
};
1409. 查询带键的排列
给定一个正整数数组 queries ,其取值范围在 1 到 m 之间。 请你根据以下规则按顺序处理所有 queries[i](从 i=0 到 i=queries.length-1):
首先,你有一个排列 P=[1,2,3,...,m]。
对于当前的 i ,找到 queries[i] 在排列 P 中的位置(从 0 开始索引),然后将它移到排列 P 的开头(即下标为 0 处)。注意, queries[i] 的查询结果是 queries[i] 在 P 中移动前的位置。
返回一个数组,包含从给定 queries 中查询到的结果。
示例 1:
输入:queries = [3,1,2,1], m = 5
输出:[2,1,2,1]
解释:处理 queries 的过程如下:
对于 i=0: queries[i]=3, P=[1,2,3,4,5], 3 在 P 中的位置是 2,然后我们把 3 移动到 P 的开头,得到 P=[3,1,2,4,5] 。
对于 i=1: queries[i]=1, P=[3,1,2,4,5], 1 在 P 中的位置是 1,然后我们把 1 移动到 P 的开头,得到 P=[1,3,2,4,5] 。
对于 i=2: queries[i]=2, P=[1,3,2,4,5], 2 在 P 中的位置是 2,然后我们把 2 移动到 P 的开头,得到 P=[2,1,3,4,5] 。
对于 i=3: queries[i]=1, P=[2,1,3,4,5], 1 在 P 中的位置是 1,然后我们把 1 移动到 P 的开头,得到 P=[1,2,3,4,5] 。
因此,包含结果的数组为 [2,1,2,1] 。
struct BIT{vector<int> a;int n;BIT(int _n): n(_n), a(_n + 1){}static int lowbit(int x){return x & (-x);}int query(int x){int ret = 0;while(x){ret += a[x];x -= lowbit(x);}return ret;}void update(int x, int dt){while(x <= n){a[x] += dt;x += lowbit(x);}}
};class Solution {
public:vector<int> processQueries(vector<int>& queries, int m) {int n = queries.size();BIT bit(m + n);vector<int> pos(m + 1);for (int i = 1; i <= m; ++i) {pos[i] = n + i;bit.update(n + i, 1);}vector<int> ans;for (int i = 0; i < n; ++i) {int& cur = pos[queries[i]];bit.update(cur, -1);ans.push_back(bit.query(cur));cur = n - i;bit.update(cur, 1);}return ans;}
};并查集
128. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
使用哈希表,先找到最小的元素,再遍历,我之前的方法是直接使用sort(nums.begin(), nums.end());
class Solution {
public:int longestConsecutive(vector<int>& nums) {unordered_set<int> num_set;for(int num : nums){num_set.insert(num);}int longstStreak = 0;for(int num : num_set){if(!num_set.count(num - 1)){int currentNum = num;int currentStreak = 1;while(num_set.count(currentNum + 1)){currentNum += 1;currentStreak += 1;}longstStreak = max(longstStreak, currentStreak);}}return longstStreak;}
};
130. 被围绕的区域
给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ ,找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

考虑边界上的‘O’,将其置为‘A’,之后再对矩阵中剩下的‘O’进行操作。
class Solution {
public:int n, m;void dfs(vector<vector<char>>& board, int x, int y){if(x < 0 || x >= n || y < 0 || y>= m || board[x][y] != 'O'){return;}board[x][y] = 'A';dfs(board, x + 1, y);dfs(board, x - 1, y);dfs(board, x, y + 1);dfs(board, x, y - 1);}void solve(vector<vector<char>>& board) {n = board.size();if(n == 0){return;}m = board[0].size();for(int i = 0; i < n; i++){dfs(board, i, 0);dfs(board, i, m - 1);} for(int i = 1; i < m - 1; i++){dfs(board, 0, i);dfs(board, n - 1, i);}for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(board[i][j] == 'A'){board[i][j] = 'O';}else if(board[i][j] == 'O'){board[i][j] = 'X';}}} }
};
二叉树
94. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
方法一:递归
class Solution {
public:void inorder(TreeNode* root, vector<int>& v){if(root == nullptr){return;}else{inorder(root->left, v);v.push_back(root->val);inorder(root->right, v);}}vector<int> inorderTraversal(TreeNode* root) {vector<int> v;inorder(root, v);return v;}
};
方法二:迭代(使用栈)
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> v;stack<TreeNode*> stk;while(!stk.empty() || root != nullptr){while(root != nullptr){stk.push(root);root = root->left;}root = stk.top();stk.pop();v.push_back(root->val);root = root->right;}return v;}
};
104. 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
方法一:深度优先搜索
class Solution {
public:int maxDepth(TreeNode* root) {if(root == nullptr){return 0;}return max(maxDepth(root->left), maxDepth(root->right)) + 1;}
};
方法二:广度优先搜索(队列)
class Solution {
public:int maxDepth(TreeNode* root) {if(root == nullptr){return 0;}queue<TreeNode*> q;q.push(root);int ans = 0;while(!q.empty()){int s = q.size();while(s > 0){TreeNode* temp = q.front();q.pop();if(temp->left){q.push(temp->left);}if(temp->right){q.push(temp->right);}s--;}ans++;}return ans;}
};
101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。

方法一:递归
class Solution {
public:bool check(TreeNode* p, TreeNode* q){if(p == nullptr && q == nullptr){return true;}if(p == nullptr || q == nullptr){return false;}return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);}bool isSymmetric(TreeNode* root) {return check(root->left, root->right);}
};
方法二:迭代(队列)
class Solution {
public:bool check(TreeNode* u, TreeNode* v){queue<TreeNode*> q;q.push(u);q.push(v);while(!q.empty()){u = q.front();q.pop();v = q.front();q.pop();if(u == nullptr && v == nullptr){continue;}if(u == nullptr || v == nullptr || u->val != v->val){return false;}q.push(u->left);q.push(v->right);q.push(u->right);q.push(v->left);}return true;}bool isSymmetric(TreeNode* root) {return check(root->left, root->right);}
};
543. 二叉树的直径
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。

class Solution {
public:int ans = 1;int depth(TreeNode* root){if(root == nullptr){return 0;}int l = depth(root->left);int r = depth(root->right);ans = max(ans, l + r + 1);return max(l, r) + 1;}int diameterOfBinaryTree(TreeNode* root) {depth(root);return ans - 1;}
};
108. 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵平衡二叉搜索树。

直接对数组进行转换
class Solution {
public:TreeNode* helper(vector<int> nums, int left, int right){if(left > right){return nullptr;}int mid = (left + right) / 2;TreeNode* root =new TreeNode(nums[mid]);root->left = helper(nums, left, mid - 1);root->right = helper(nums, mid + 1, right);return root; }TreeNode* sortedArrayToBST(vector<int>& nums) {return helper(nums, 0, nums.size() - 1);}
};
相关文章:

LeetCode刷题【树状数组、并查集、二叉树】
目录 树状数组307. 区域和检索 - 数组可修改406. 根据身高重建队列673. 最长递增子序列的个数1409. 查询带键的排列 并查集128. 最长连续序列130. 被围绕的区域 二叉树94. 二叉树的中序遍历104. 二叉树的最大深度101. 对称二叉树543. 二叉树的直径108. 将有序数组转换为二叉搜索…...
使用POI以OLE对象的形式向excel中插入附件(pdf为例)
前言: 最近在使用easyExcel操作excel文件时,一直想找到一个方法可以往excel中填充附件,但是目前只发现POI可以插入附件,于是将方法记录如下: 实现: 这个方法主要是使用 Apache POI 的 HSSFWorkbook 类来…...
——SBP的初始设置和脚本编译)
Unity构建详解(2)——SBP的初始设置和脚本编译
【SwitchToBuildPlatform】 核心逻辑如下 EditorUserBuildSettings.SwitchActiveBuildTarget(m_Parameters.Group, m_Parameters.Target); 直接调用切换平台的接口,一般来说,这个步骤不会执行,我们打包时肯定会事先将平台切换好的 【Rebu…...
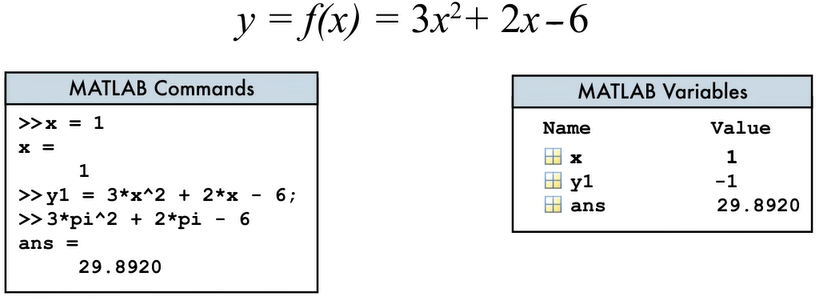
Matlab使用教程(持续更新)
1. Matlab Matlab被广泛的应用在数据分析,汽车仿真,机器人以及医学研究等众多方面。 它可以帮助我们理解研究复杂的系统。 在60年代和70年代,计算机使得科学家和工程师完成了以前不可能进行的计算;但是需要懂得计算机编程。 C…...

管理能力学习笔记一:角色转身
管理能力学习是为了解决角色转身后面临的更多更复杂的的问题。初晋管理层,需要转变工作习惯,学会分配时间。 角色转身 建立“授权”意识 通过匹配工作内容与下属员工能力,分配工作,避免陷入下属能力不足 -> 不愿授权 -> 下…...

Redis面试题 概要
文章目录 Redis面试题 概要缓存穿透布隆过滤器缓存击穿缓存雪崩数据同步数据持久化数据过期策略Redis的数据淘汰策略Redis + Lau 限流Redis面试题 概要 Redis是一个基于 C 语言开发的开源 NoSQL 数据库,Redis 的数据是保存在内存中的(内存数据库,支持持久化),因此读写速度…...

原型,模板,策略,适配器模式
原型模式 原型模式(创建型模式),核心思想就是:基于一个已有的对象复制一个对象出来,通过复制来减少对象的直接创建的成本。 总结一下,原型模式的两种方法,浅拷贝只会复制对象里面的基本数据类型…...

Ollama 在本地快速启动并执行LLM【大语言模型】
文章目录 1. 什么是Ollama?1.1. SDK库1.2. 提供的api服务1.3. [支持的LLM](https://ollama.com/library)2. 如何安装2.1.下载docker镜像2.2. 启动docker容器3. 如何使用?3.1. 如何加载模型3.2. 使用 Ollama CLI 进行推理3.3. 使用 Ollama API 进行推理参考1. 什么是Ollama?...

ubuntu : 无法修正错误,因为您要求某些软件包保持现状,就是它们破坏了软件包间的依赖关系。
往后看,90%能解决你的问题 原文链接:学一下 (suxueit.com) 我相信很多人刚使用ubuntu都遇到过这个问题,如果没有遇到,可能是你运气好使用了正确的软件源 libprotobuf-dev : 依赖: zlib1g-dev 但是它将不会被安装 zlib1g-dev : 依…...

瑞芯微RK3576|触觉智能:开启科技新篇章
更多产品详情可关注深圳触觉智能官网! “瑞芯微,创新不止步!”——全新芯片RK3576即将震撼登场。指引科技风潮,创造未来无限可能!这款芯片在瑞芯微不断创新和突破的道路上,不仅是对过往成就的完美延续&…...

Visual Studio 2013 - 清理
Visual Studio 2013 - 清理 1. 清理1.1. 工程清理1.2. 解决方案清理 References 1. 清理 Debug Release 1.1. 工程清理 (right mouse click on the project) -> 清理 1.2. 解决方案清理 (right mouse click on the solution) -> 清理解决方案 References [1] Yongq…...
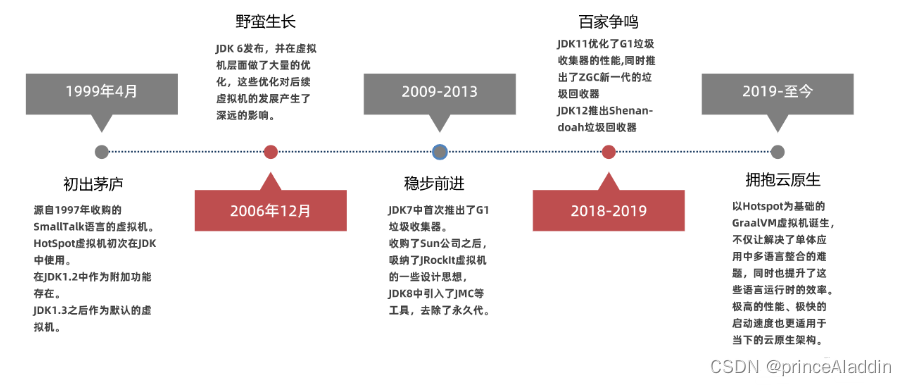
1、初识JVM
一、JVM是什么? JVM的英文全称是 Java Virtual Machine,其中文译名为Java虚拟机。它在本质上就是是一个运行在计算机上的程序,他的职责是运行Java字节码文件。 JVM执行流程如下 二、JVM有哪些功能? 2.1 解释和运行 对字节码文…...
(七))
JavaScript 权威指南第七版(GPT 重译)(七)
第十六章:用 Node 进行服务器端 JavaScript Node 是 JavaScript 与底层操作系统的绑定,使得编写 JavaScript 程序读写文件、执行子进程和在网络上通信成为可能。这使得 Node 作为以下用途变得有用: 现代替代 shell 脚本的方式,不…...

从零开始搭建游戏服务器 第四节 MongoDB引入并实现注册登录
目录 前言正文添加依赖安装MongoDB添加MongoDB相关配置创建MongoContext类尝试初始化DB连接实现注册功能测试注册功能实现登录逻辑测试登录流程 结语下节预告 前言 游戏服务器中, 很重要的一点就是如何保存玩家的游戏数据. 当一个服务端架构趋于稳定且功能全面, 开发者会发现服…...

【Unity】宏定义Scripting Define Symbols
1.宏的用处 我们在使用Unity开发的时候,经常需要根据不同环境执行不同的代码 比如安卓手机和苹果手机获取路径代码 这个时候,宏就派上用场了。 代码示例: //获取路径public string GtePath(){//不同平台,取不同的存储路径string…...

算法 之 排序算法
🎉欢迎大家观看AUGENSTERN_dc的文章(o゜▽゜)o☆✨✨ 🎉感谢各位读者在百忙之中抽出时间来垂阅我的文章,我会尽我所能向的大家分享我的知识和经验📖 🎉希望我们在一篇篇的文章中能够共同进步!!&…...

Prism:打造WPF项目的MVVM之选,简化开发流程、提高可维护性
概述:探索WPF开发新境界,借助Prism MVVM库,实现模块化、可维护的项目。强大的命令系统、松耦合通信、内置导航,让您的开发更高效、更流畅 在WPF开发中,一个优秀的MVVM库是Prism。以下是Prism的优点以及基本应用示例&a…...
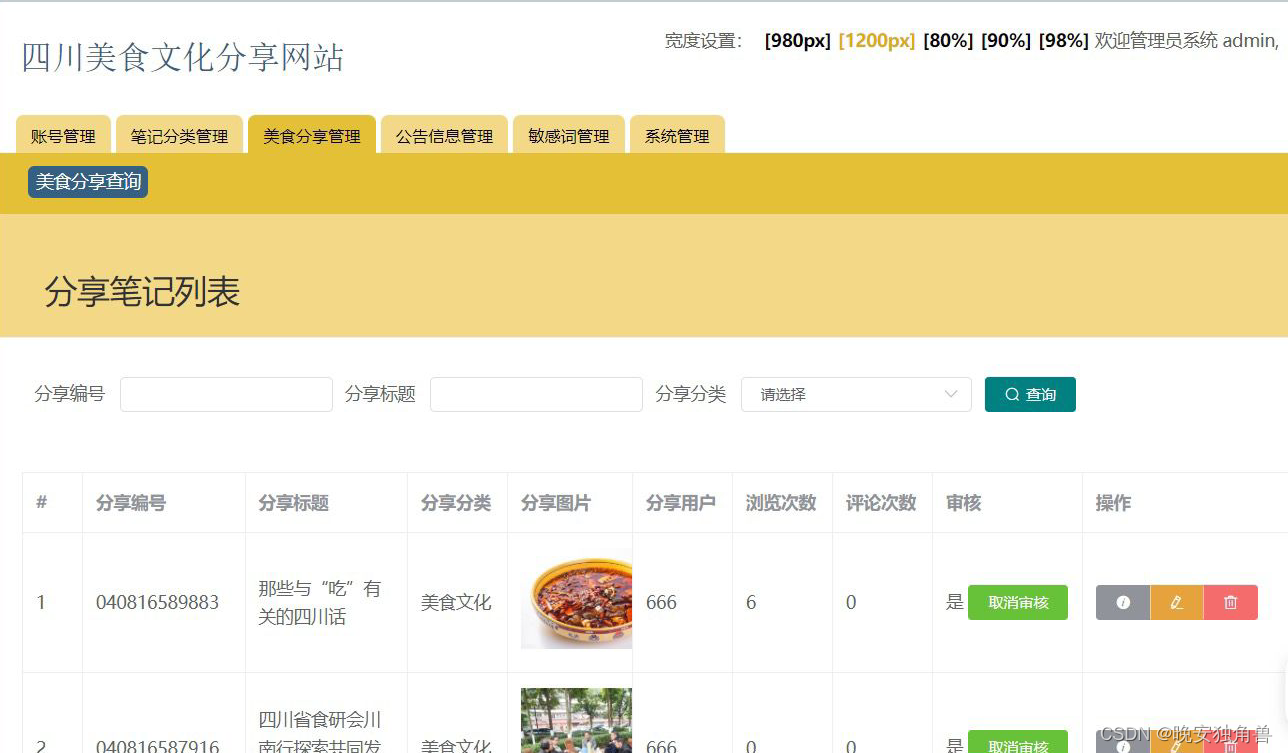
Springboot+vue的四川美食分享网站+数据库+报告+免费远程调试
项目介绍: Springbootvue的四川美食分享网站。Javaee项目,springboot vue前后端分离项目 本文设计了一个基于Springbootvue的前后端分离的四川美食分享网站,采用M(model)V(view)C(controller&am…...
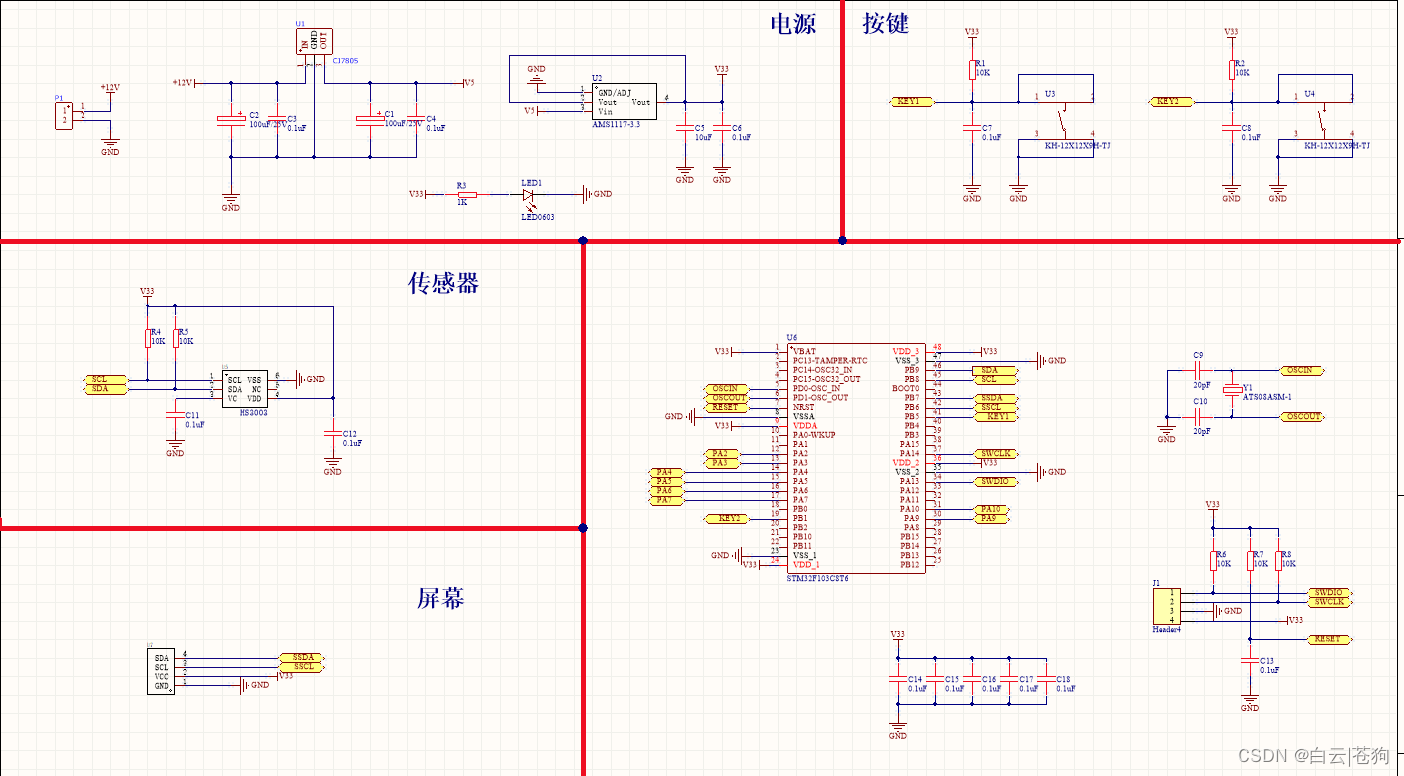
温湿度项目V1.0——原理图设计
工程 首先要有安装好的Altium Designer软件。新建工程,添加sch、pcb文件;新建原理图库和PCB库。画原理图之前应该要有自己的原理库,可以从自己的原理图库中拖元器件到原理图中。那么就要先画原理图库的元器件,再画该元器件的封装…...

H5 与 App、网页之间的通信
前言 本文整理工作中 H5 嵌入 Android、iOS 与 PC 网页后,如何与各端通信。(提供 H5 端的代码) 环境判断 const ua navigator.userAgent.toLowerCase()const isAndroid /android/i.test(ua)const isIos /iphone|ipod|ios/i.test(ua)cons…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...
