DS-红黑树(RBTree)
一.红黑树
1.1 红黑树的起源
当对对AVL树做一些结构修改的操作时候,性能较为低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。
因此1972年Rudolf Bayer提出的对称二叉B树(Symmetric Binary B-Trees),随后在1978年Leo J. Guibas和Robert Sedgewick的工作中进一步发展和完善,最终形成了现代意义上的红黑树,它通过简单的规则和较少的旋转操作实现了有效的自平衡,广泛应用于各类需要高效查找、插入和删除操作的场合,例如在Java集合框架中的TreeMap和TreeSet类,以及哈希表中解决冲突时采用的链表+红黑树混合结构。
1.2 红黑树的概念
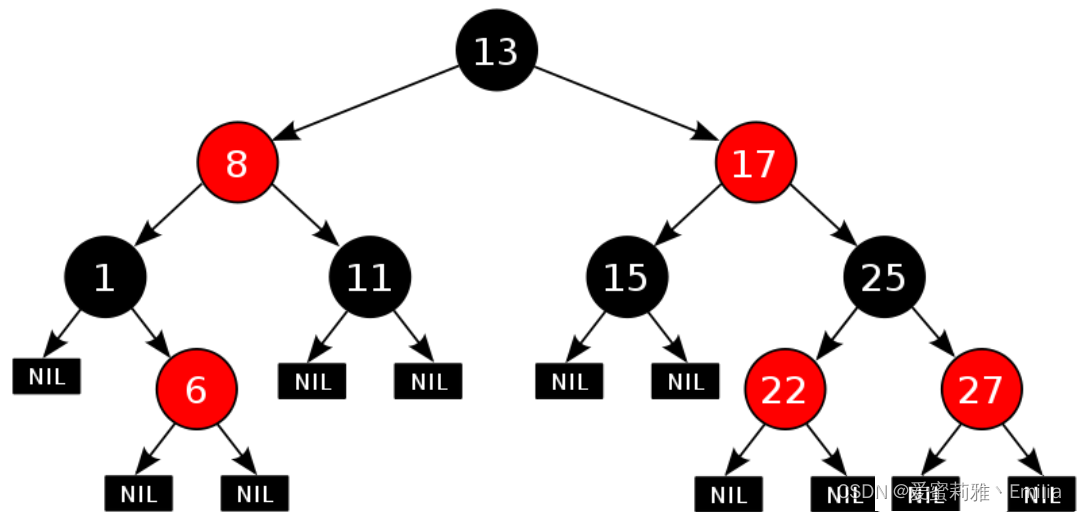
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍,因而是接近平衡的。
红黑树具有以下性质:
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
1.3 红黑树节点的定义
enum Color
{RED,BLACK
};template<typename T>
struct RBTreeNode
{RBTreeNode(const T& data): _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent; //父节点T _data;Color _col; //颜色
};
1.4 红黑树的插入
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
- 按照二叉搜索的树规则插入新节点。
- 检测新节点插入后,红黑树的性质是否造到破坏。
bool insert(const T& data)
{if (_root == nullptr){_root = new Node(data);return true;}Node* grandparent = nullptr;Node* uncle = nullptr;Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (data < cur->_data){cur = cur->_left;}else if (data > cur->_data){cur = cur->_right;}else{return false;}}cur = new Node(data);if (data < parent->_data){parent->_left = cur;}else if (data > parent->_data){parent->_right = cur;}else{assert(false);}cur->_parent = parent;while (parent && parent->_col == RED){grandparent = parent->_parent;if (grandparent){if (parent == grandparent->_left){uncle = grandparent->_right;}else{uncle = grandparent->_left;}}else{break;}if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;}else{cur = Rotate(grandparent, parent, cur);}parent = cur->_parent;_root->_col = BLACK;}return true;
}
大致思路如下:
以下简称插入节点为cur,cur的父节点为parent,parent的父节点为grandparent,parent的兄弟节点为uncle。
- 先先按照二叉搜索树的规则将节点插入到红黑树中,节点颜色为红色。
- 插入后,红黑树的性质可能遭到破坏,此时就要根据红黑树的性质进行检测。
- cur插入后,如果parent颜色为黑色,则没有破坏红黑树的性质,插入结束。
- 若parent为红色,则此时有两种情况(uncle为红,uncle为黑/uncle不存在)
- uncle为红时,将parent和uncle变为黑色,grandparent变为红色,然后把grandparent视为cur,继续向上调整。
- uncle为黑/uncle不存在时,进行旋转。 (旋转在1.5处详细解释)
1.5 红黑树的旋转
此处的旋转与AVL树的旋转思路较为相似。
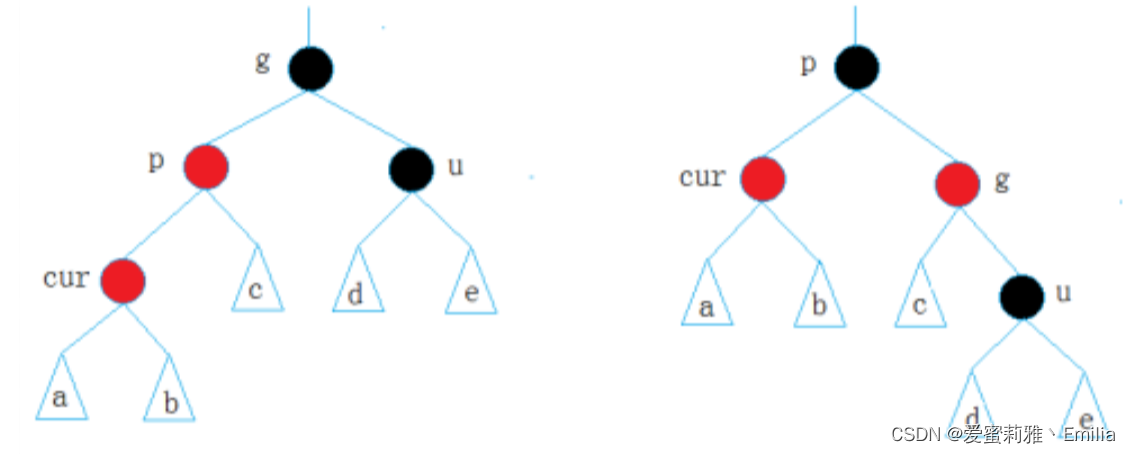
当uncle为黑/uncle不存在时,parent为cur的(左/右)孩子且parent为grandparent的(左/右)孩子,进行(右单旋)/(左单旋)。
右单旋
void RotateR(Node* parent)
{Node* ppnode = parent->_parent;Node* cur = parent->_left;Node* cur_right = cur->_right;if (ppnode){if (ppnode->_left == parent){ppnode->_left = cur;}else if (ppnode->_right == parent){ppnode->_right = cur;}else{assert(false);}}else{_root = cur;}cur->_parent = ppnode;parent->_left = cur_right;if (cur_right){cur_right->_parent = parent;}cur->_right = parent;parent->_parent = cur;
}
左单旋
void RotateL(Node* parent)
{Node* ppnode = parent->_parent;Node* cur = parent->_right;Node* cur_left = cur->_left;if (ppnode){if (ppnode->_right == parent){ppnode->_right = cur;}else if (ppnode->_left == parent){ppnode->_left = cur;}else{assert(false);}}else{_root = cur;}cur->_parent = ppnode;parent->_right = cur_left;if (cur_left){cur_left->_parent = parent;}cur->_left = parent;parent->_parent = cur;
}
当uncle为黑/uncle不存在时,parent为cur的(右/左)孩子且parent为grandparent的(左/右)孩子,进行(右单旋)/(左单旋)。
Node* Rotate(Node* grandparent, Node* parent, Node* cur)
{if (parent == grandparent->_left){if (cur == parent->_left){RotateR(grandparent);parent->_col = RED;grandparent->_col = BLACK;cur->_col = BLACK;return parent;}else{RotateL(parent);RotateR(grandparent);parent->_col = BLACK;grandparent->_col = BLACK;cur->_col = RED;return cur;}}else{if (cur == parent->_left){RotateR(parent);RotateL(grandparent);parent->_col = BLACK;grandparent->_col = BLACK;cur->_col = RED;return cur;}else{RotateL(grandparent);parent->_col = RED;grandparent->_col = BLACK;cur->_col = BLACK;return parent;}}
1.6 红黑树的特点与应用
- 红黑树是一棵不追求绝对平衡的二叉搜索树,其只需保证最长路径不超过最短路径的2倍,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优。
- 红黑树在C++ STL库中 map/set 等结构中充当底层结构,据说在java中哈希表中的哈希桶下的链表长度超过一定的阈值时,也会转换为红黑树提高效率。使得在处理大量冲突键时,极大的缓解了链表过长导致的哈希表查找效率退化。
1.7 完整代码
#pragma once
#include <iostream>
#include <assert.h>
using namespace std;enum Color
{RED,BLACK
};template<typename T>
struct RBTreeNode
{RBTreeNode(const T& data): _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Color _col;
};template<typename T>
class RBTree
{
public:typedef RBTreeNode<T> Node;RBTree():_root(nullptr){}bool insert(const T& data){if (_root == nullptr){_root = new Node(data);return true;}Node* grandparent = nullptr;Node* uncle = nullptr;Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (data < cur->_data){cur = cur->_left;}else if (data > cur->_data){cur = cur->_right;}else{return false;}}cur = new Node(data);if (data < parent->_data){parent->_left = cur;}else if (data > parent->_data){parent->_right = cur;}else{assert(false);}cur->_parent = parent;while (parent && parent->_col == RED){grandparent = parent->_parent;if (grandparent){if (parent == grandparent->_left){uncle = grandparent->_right;}else{uncle = grandparent->_left;}}else{break;}if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;}else{cur = Rotate(grandparent, parent, cur);}parent = cur->_parent;_root->_col = BLACK;}return true;}Node* get_Root(){return _root;}bool checkColour(Node* root, int blacknum, int benchmark){if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_col == BLACK){++blacknum;}if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_data << "出现连续红色节点" << endl;return false;}return checkColour(root->_left, blacknum, benchmark)&& checkColour(root->_right, blacknum, benchmark);}bool isBalance(){return isBalance(_root);}int height(){return height(_root);}
private:Node* _root;void RotateR(Node* parent){Node* ppnode = parent->_parent;Node* cur = parent->_left;Node* cur_right = cur->_right;if (ppnode){if (ppnode->_left == parent){ppnode->_left = cur;}else if (ppnode->_right == parent){ppnode->_right = cur;}else{assert(false);}}else{_root = cur;}cur->_parent = ppnode;parent->_left = cur_right;if (cur_right){cur_right->_parent = parent;}cur->_right = parent;parent->_parent = cur;}void RotateL(Node* parent){Node* ppnode = parent->_parent;Node* cur = parent->_right;Node* cur_left = cur->_left;if (ppnode){if (ppnode->_right == parent){ppnode->_right = cur;}else if (ppnode->_left == parent){ppnode->_left = cur;}else{assert(false);}}else{_root = cur;}cur->_parent = ppnode;parent->_right = cur_left;if (cur_left){cur_left->_parent = parent;}cur->_left = parent;parent->_parent = cur;}Node* Rotate(Node* grandparent, Node* parent, Node* cur){if (parent == grandparent->_left){if (cur == parent->_left){RotateR(grandparent);parent->_col = RED;grandparent->_col = BLACK;cur->_col = BLACK;return parent;}else{RotateL(parent);RotateR(grandparent);parent->_col = BLACK;grandparent->_col = BLACK;cur->_col = RED;return cur;}}else{if (cur == parent->_left){RotateR(parent);RotateL(grandparent);parent->_col = BLACK;grandparent->_col = BLACK;cur->_col = RED;return cur;}else{RotateL(grandparent);parent->_col = RED;grandparent->_col = BLACK;cur->_col = BLACK;return parent;}}}bool isBalance(Node* root){if (root == nullptr)return true;if (root->_col != BLACK){return false;}// 基准值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}return checkColour(root, 0, benchmark);}int height(Node* root){if (root == nullptr)return 0;int leftHeight = height(root->_left);int rightHeight = height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}
};
————————————————————
感谢大家观看,不妨点赞支持一下吧[doge]
如有错误,随时纠正,谢谢大家
相关文章:
DS-红黑树(RBTree)
一.红黑树 1.1 红黑树的起源 当对对AVL树做一些结构修改的操作时候,性能较为低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。 因此1972年Rudolf…...
ubuntu 如何使用阿里云盘
你好,我是 shengjk1,多年大厂经验,努力构建 通俗易懂的、好玩的编程语言教程。 欢迎关注!你会有如下收益: 了解大厂经验拥有和大厂相匹配的技术等 希望看什么,评论或者私信告诉我! 文章目录 一…...

sqlite3 交叉编译
#1.下载源码并解压 源码路径如下,下载autoconf版本 SQLite Download Page 解压 tar -zxvf sqlite-autoconf-3450200.tar.gz cd sqlite-autoconf-3450200 mkdir build # 2. 配置源代码 # 假设你已经安装了交叉编译工具链,如gcc-arm-linux-gnueabih…...

【AI生成文章】flutter ChangeNotifierProvider 实用场景举例
内容由Ai 大模型生成,不能完全保障真实 ChangeNotifierProvider 是 Flutter 中一个非常实用的工具,用于在应用程序中管理和传递状态。以下是一些实用的场景举例: 1. 用户信息管理 在应用程序中,用户信息(如用户名、…...
)
【0274】从shared init file或local init file加载relation cache(2 - 1)
上一篇: 【0273】深入分析 relcache(relation descriptor cache)初始化第一阶段(1) 【0264】深入分析relcache(relation descriptor cache)缓存初始化第2阶段(2) 1. 前言 本文内容是作为《【0264】深入分析relcache(relation descriptor cache)缓存初始化第2阶段…...
蓝桥杯-02-2023蓝桥杯c/c++省赛B组题目
参考 2023 年第十四届蓝桥杯 C/C B组省赛题解 2023蓝桥杯c/c省赛B组题目(最全版): A:日期统计 这题方法应该很多,没有和别人讨论想法。我的解法思路是:先 load 函数生成所有这一年的合法日期,然后枚举所有可以从数据…...

欧拉筛+并查集
集合 - 洛谷 std::vector<int> minp, primes,primes1;void sieve(int n,int p) {minp.assign(n 1, 0);primes.clear();for (int i 2; i < n; i) {if (minp[i] 0) {minp[i] i;primes.push_back(i);}for (auto p : primes) {if (i * p > n) {break;}minp[i * p]…...
》)
《桥接模式(极简c++)》
本文章属于专栏《设计模式(极简c版)》 继续上一篇《原型模式(极简c)》。本章简要说明桥接模式。本文分为模式说明、本质思想、实践建议、代码示例四个部分。 模式说明 方案: 将抽象部分与它的实现部分分离,…...
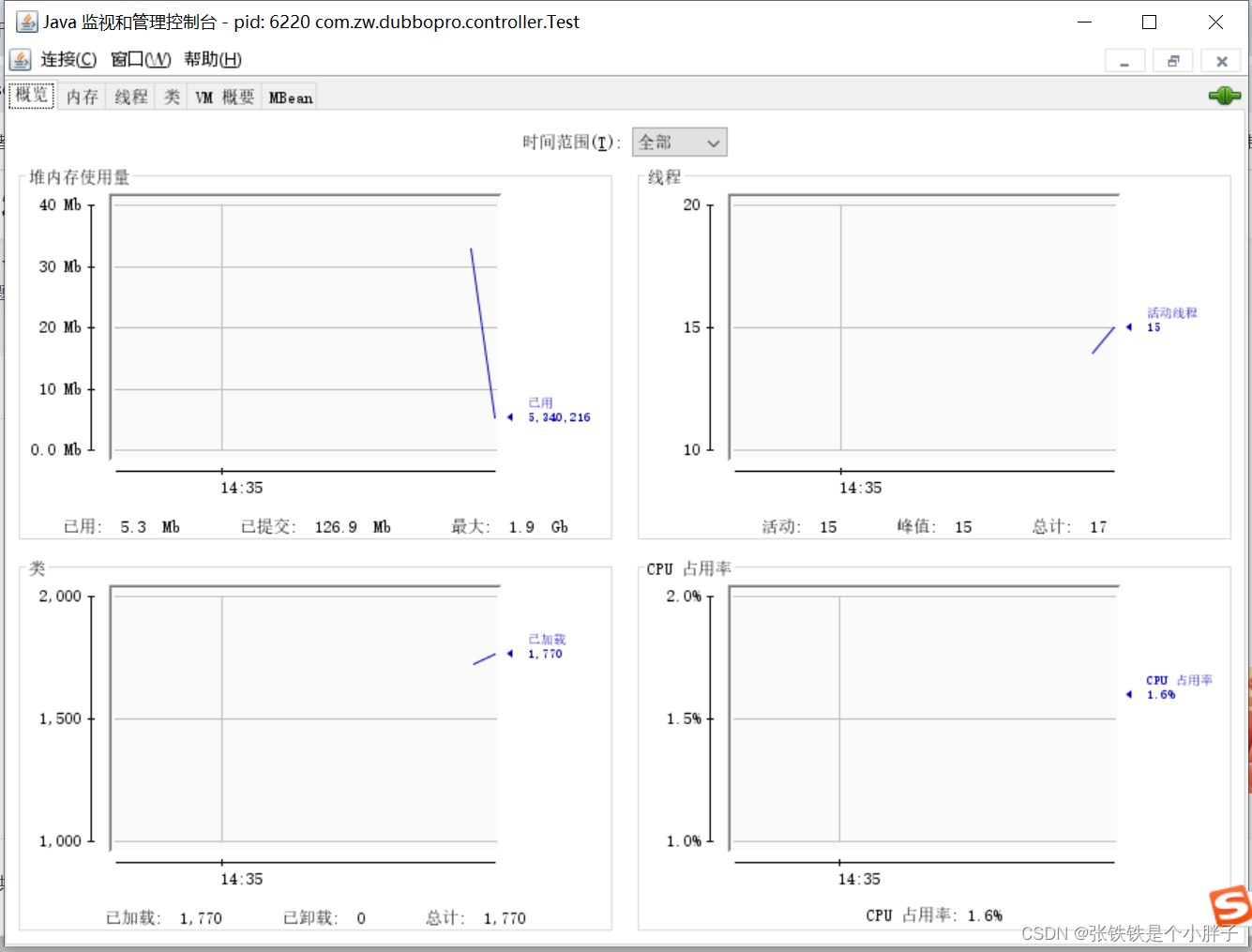
jconsole的使用
前提 已安装jdk 使用步骤 1、命令行输入jconsole...
JavaScript详细教程
文章目录 前言一、代码位置二、注释三、变量1.字符串类型2.数组3.对象(字典) 四、条件语句五、函数六、DOM模板 前言 JavaScript 是一种脚本编程语言,它可以在网页上实现复杂的功能,网页展现给你的不再是简单的静态信息࿰…...

Hive自定义GenericUDF函数
Hive自定义GenericUDF函数 当创建自定义函数时,推荐使用 GenericUDF 类而不是 UDF 类,因为 GenericUDF 提供了更灵活的功能和更好的性能。以下是使用 GenericUDF 类创建自定义函数的步骤: 编写Java函数逻辑:编写继承自 GenericUDF…...

伊理威科技:抖音开网店新手刚做选啥品
在数字浪潮中,抖音不仅是展示才艺的舞台,更是创业者的新天地。新手若想在这片热土上开垦网店,选品便是首要课题。选择产品如同种下希望的种子,既要考量土壤肥沃度,也得预测风雨适宜期。 兴趣与专长是选品的罗盘。热爱所…...

【爬虫】专栏文章索引
为了方便 快速定位 和 便于文章间的相互引用等 作为一个快速准确的导航工具 爬虫 目录: (一)web自动化和接口自动化 (二)实战-爬取Boss直聘信息数据...
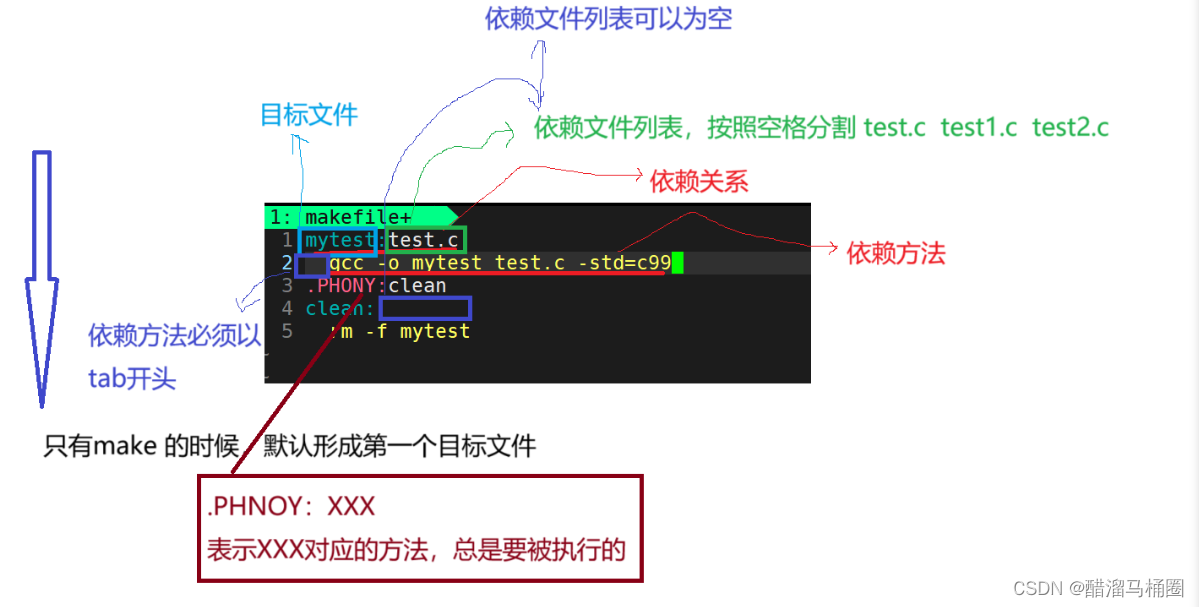
【Linux】Linux开发工具-vim / 编译器-gcc/g++ / 调试器-gdb / git操作 / 项目自动化构建工具-make/Makefile
主页:醋溜马桶圈-CSDN博客 专栏:Linux_醋溜马桶圈的博客-CSDN博客 gitee:mnxcc (mnxcc) - Gitee.com 目录 1.在Linux写自己的第一个程序 1.1 nano指令 1.2 nano指令的使用 1.2.1 介绍 1.2.2 演示 1.2.2.1 创建.c文件 1.2.2.2 nano cod…...

解决VM重新打开后找不到共享文件夹的问题
我的问题是之前按照网上的文档设置了vm的共享文件夹,能成功使用,但是问题是下一次打开之后就找不到了,虚拟机设置里共享文件夹是启用的,文件夹也完成了映射网络驱动器,但是就是找不到共享文件夹 解决方法:…...

uni app 空挡接龙
pc游戏 空挡接龙 还不完整。现在没时间搞了记录在这里,等以后有时间了再继续搞。 <template><view class"page_main"><view class"contentone"><canvas class"canvas_cla" style"z-index: 1;" canva…...

oracle表备份及还原
工作中,经常使用Navicat访问及操作Oracle数据库,备份表非常方便Ctrlc、Ctrlv;最近备份表,发现这种操作有问题;数据表有2条检查,使用Ctrlc、Ctrlv操作,发现新备份的表出现4条检查,再对…...

牛客小白月赛89补题1(ABCD)(偏难)
评价: 高情商:收获很大 ,让自己进一步认清自己。 低情商:题目难,自己太菜了。 今天还有一些其他事,剩下的题明天再补。 我们从a题开始吧: A.签到 我们只要看看其中的max与min是否不符合即可…...
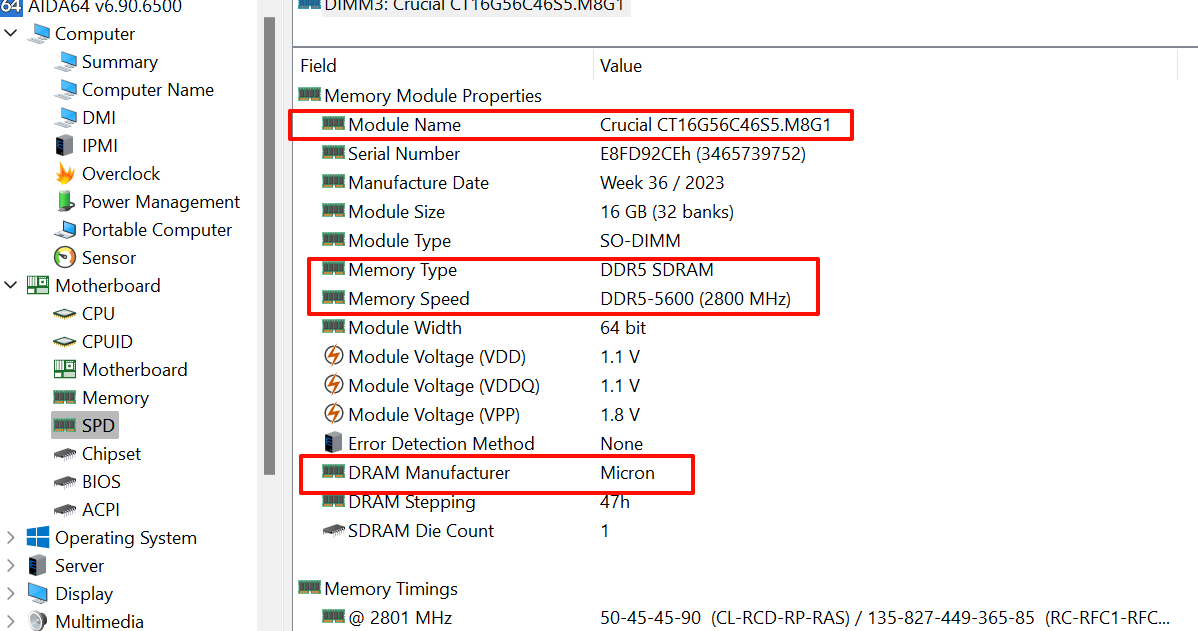
内存条@电脑支持的最大内存@升级内存硬件
文章目录 电脑支持的最大内存规格cpu官网查看支持的规格命令行查看脚本化 DDR内存LPDDR内存内存升级扩展👺插槽检查板载内存SPD内存厂商其他 内存参数👺性能指标使用软件查看更多内存相关的软件工具 电脑支持的最大内存规格 确认电脑最大支持内存大小和频…...

如何了解AI基础概念
1. **在线课程和教程:** - 寻找在线AI课程或教程,例如Coursera、edX、Udemy等平台上的课程。这些课程通常会从基础概念开始介绍,逐步深入。 2. **书籍阅读:** - 阅读与AI相关的书籍,如《Python深度学习》、《机…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...