暴力快速入门强化学习
强化学习算法的基本思想(直觉)
众所周知,强化学习是能让智能体实现某个具体任务的强大算法。
强化学习的基本思想是让智能体跟环境交互,通过环境的反馈让智能体调整自己的策略,从反馈中学习,不断学习来得到最优的策略(即以最优的方式实现某个具体任务)。
形式化强化学习的直觉(将算法的直觉变成可以量化的数学形式)
经过大量的研究,人们探索出一种适用于实现强化学习这个目标的数学框架——马尔科夫决策过程。
其实这个框架也不复杂,通过理解强化学习的思想,想想就知道起码得有这些简单的东西:
- 智能体的动作(肯定要行动,才能达成某个任务的目的)
- 环境的状态(智能体要根据环境状态决定自己要怎么样行动)
- 环境的反馈(智能体每次行动完,需要得到反馈才能知道自己的行动好还是不好)
仅仅从直觉上看差不多是这三个,因为直觉还是比较抽象的,要带入实际的案例才会发现还缺少哪些东西。
比如随便想想,下围棋的时候,是不是从下棋一开始到胜利都全部被智能体接管了,所以在这个过程中智能体需要连续进行行动,那么问题就来了,我定义只有下棋最终胜利的那一步行动才有奖励(正反馈),其余行动都没有奖励,这个定义很合理吧,但是在这个过程中每一步都没有奖励,也就相当于没有反馈,那智能体还怎么学习呢?
所以这个时候又要靠直觉思考一下,虽然围棋在胜利前每一步都没有奖励,但是这并不代表每一步都没有价值,如果是一个围棋高手,他下的每一步棋都是为了最后的胜利而铺垫的,可以说每一步棋的价值都很大。所以直觉上想通了,怎么把直觉转化为数学上可以精确量化的定义呢?
其实可以使用累积奖励作为该行动的价值,具体就是从当前状态出发,一直按照某个决策行动下去,到最后游戏结束得到的奖励总和,公式很简单就是 G ( S t ) = Σ k = t R k + 1 G(S_t) = \Sigma_{k=t} R_{k+1} G(St)=Σk=tRk+1,即表示从时刻t开始,棋盘状态为S,该时刻的状态按照智能体的策略一直执行下去,到最终游戏结束,得到的奖励累计之和,就用这个表示当前状态S的价值。不过实操起来还是有问题,第一,我希望以尽可能短的步数赢下比赛,而这个公式似乎没有对于步数的惩罚,1000步赢下比赛和100赢下比赛的奖励总和是一样的,所以要进行修正,这里我们引入一个折扣因子 γ ∈ [ 0 , 1 ] \gamma \in [0, 1] γ∈[0,1],每走一步就要将当前行动得到的奖励乘以 γ \gamma γ,这样步数越多,最后得到的奖励越少,公式是: G ( S t ) = Σ k = 0 γ k R t + k + 1 G(S_t) = \Sigma_{k=0} \gamma^kR_{t+k+1} G(St)=Σk=0γkRt+k+1。
这样看起来就很完美了是吧?还没完,这个累加公式看起来很不错,但是缺少了关键的信息,这个公式是把每次行动后跳到一个状态时得到的奖励进行折扣累加,但是我怎么知道从一个状态做出行动后会跳到哪一个动作呢?假设t时刻,环境处于状态 S t S_t St,智能体进行行动 A t A_t At之后,环境变成什么样子了?即我想知道某个状态执行某个动作之后,跳转到下一个状态这之间的映射关系,即 S t + 1 = f ( S t , A t ) S_{t+1} = f(S_t, A_t) St+1=f(St,At)这个函数具体是什么样子,不过这个函数映射的形式是确定性的,就是说 S t S_t St和 A t A_t At确定了之后, S t + 1 S_{t+1} St+1也就唯一确定了,但很多情况往往是不确定的,比如你每学期你的状态都是摆烂,然后考试前你的行动都是通宵复习,但有时候你挂科了,有时候你及格了,还有时候你满分了,这就是不确定的,这是有概率的,当然在及格边缘的概率更大,所以我们定义这个环境变换的映射情况就叫做状态转移概率,即 P ( S t + 1 ∣ S t , A t ) P(S_{t+1} \mid S_t,A_t) P(St+1∣St,At)。当然对于游戏来说都是一般都是确定的,概率直接为1或者0就行。
总结一下,马尔科夫决策模型包含以下几个东西:
- S S S:环境状态的集合
- A A A:智能体动作的集合
- r ( s , a ) r(s,a) r(s,a):每个状态下行动后得到奖励函数,人为定义
- P ( s ′ ∣ s , a ) P(s'\mid s, a) P(s′∣s,a) :环境的状态转移概率
- γ \gamma γ:折扣因子
马尔科夫决策过程终于写完了,啰啰嗦嗦写了一大堆,强化学习的思想直觉两句话就搞定,把强化学习的思想形式化需要写这么多,看来直觉是不负责任的,将直觉转化成数学才是负责任的,难的东西。终于知道为什么有的论文明明很简单的方法,却能写那么多页了,因为将直觉形式化、数学化这中间有很多细节需要商榷和讨论。
不过这还只是强化学习算法的前提框架,在这个框架下各种算法的挖掘才是大头。
利用马尔科夫决策过程提供的抽象框架来真正得到最优决策
写累了,前面说一大堆,其实最后都是为了能够求解出智能体针对某个具体任务的最优决策。有了前面的基础,后面的求解算法其实没那么复杂了,我也写累了,所以这部分直接精简逻辑,让最本质的东西呈现出来,很简单。
我们想得到最优策略,这只是直觉上,还是那句话,形式化到数学上,其实就是最大化累计奖励。从某个状态出发,智能体进行一系列的决策已经得到了最大的累计奖励,再也没有别的决策能得到比这个决策更大的累计奖励了,所以自然该决策就是最优决策。
现在这个圈子内把这个累计奖励直接叫做回报(Return),用 G t G_t Gt表示从t时刻(或者从某个状态开始)一直到结束得到的累计奖励,那么随便游戏从什么时候什么状态开始,我都希望该智能体的决策能够得到最大化的回报。
π \pi π代表的是智能体的策略,更具体一点,就是在状态 s s s下采取行动 a a a的策略,同样,策略一般也是用一个概率分布表示,即 π ( a ∣ s ) \pi(a \mid s) π(a∣s)。前面说到用累计奖励作为状态的价值,其实就是用某个状态的回报作为该状态的价值,不过因为回报 G t G_t Gt其实是一个随机变量,由状态转移概率 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a)和 π ( a ∣ s ) \pi(a |s) π(a∣s)这两个分布决定,所以不好直接量化状态的价值,不过随机变量的期望是一个确定的值,可以作为量化的标准,所以很自然的,某个状态s的价值就可以化为这样一个状态价值函数: v π ( s ) = E ( G t ∣ S t = s ) v_{\pi}(s) = E(G_t|S_t=s) vπ(s)=E(Gt∣St=s),这个方程表示从t时刻开始,环境的状态是 s s s,在这个给定的条件下, G t G_t Gt(回报)的期望就是状态s的价值。
那现在其实就秀一下数学推理能力,把 v π ( s ) = E ( G t ∣ S t = s ) v_{\pi}(s) = E(G_t|S_t=s) vπ(s)=E(Gt∣St=s)这个公式展开,然后经过三四步推理,很容易就能得到(推理要注意条件期望怎么展开怎么求,这一步有点绕,不过小心点还是很容易就能推出来): v π ( s ) = E [ R t + 1 + γ v π ( s ′ ) ] v_{\pi}(s) = E[R_{t+1} + \gamma v_{\pi}(s')] vπ(s)=E[Rt+1+γvπ(s′)]这就是贝尔曼方程,即当前状态 s s s的价值可以用下一个状态 s ′ s' s′的价值来表示。贝尔曼最优方程就是价值最大的那个 v π ∗ = m a x π v ( s ) v_{\pi}^* = max_{\pi}v(s) vπ∗=maxπv(s)。
那这个时候不要忘记我们的初心,我们如果得到了最大的 v ( s ) v(s) v(s),代表当前的策略是最优的策略,但这个最优的策略我怎么形式化表示出来呢?换句话说,处于状态 s s s时,我要选择什么样的动作a呢?显然在状态s下,我要选择价值最大的那个 a a a,这个价值最大是不是很熟悉,同理我们也可以定义状态-动作函数 q π ( s , a ) q_{\pi}(s,a) qπ(s,a),那这个 q π ( s , a ) q_{\pi}(s,a) qπ(s,a)等于什么呢?还是跟之前一样的,还是用累计奖励呗! q π ( s , a ) = E [ R t + 1 + γ q π ( s ′ , a ′ ) ∣ S t = s , A t = a ] q_{\pi}(s,a) = E[R_{t+1}+\gamma q_{\pi}(s',a') | S_t=s,A_t=a] qπ(s,a)=E[Rt+1+γqπ(s′,a′)∣St=s,At=a]
直观来看 q π ( s , a ) q_{\pi}(s,a) qπ(s,a)与 v π ( s ) v_{\pi}(s) vπ(s)应该满足这样的关系:在状态s下,智能体可以有多个动作可以选择: a 1 , a 2 , . . . a_1,a_2,... a1,a2,...,所以 v π ( s ) v_{\pi}(s) vπ(s)应该是 q π ( s , a ) q_{\pi}(s,a) qπ(s,a)关于a的期望,即: v π ( s ) = Σ a ∈ A π ( a ∣ s ) q π ( s , a ) v_{\pi}(s) = \Sigma_{a \in A}\pi(a|s)q_{\pi}(s,a) vπ(s)=Σa∈Aπ(a∣s)qπ(s,a)
言归正传,我要得到最优策略的形式化表述,其实就是希望在每个状态下面采取价值最大的那个行动,即希望找到 q π ∗ ( s , a ) = m a x π q ( s , a ) q_{\pi}^*(s,a) = max_{\pi}q(s,a) qπ∗(s,a)=maxπq(s,a)。那么根据 v π ( s ) v_{\pi}(s) vπ(s)和 q π ( s , a ) q_{\pi}(s,a) qπ(s,a)的关系,其实可以推导出来 q π ( s , a ) = R s a + γ Σ s ′ ∈ S P s s ′ a v π ( s ′ ) q_{\pi}(s,a) = R_s^a+\gamma \Sigma_{s'\in S}P_{ss'}^av_{\pi}(s') qπ(s,a)=Rsa+γΣs′∈SPss′avπ(s′)。那其实问题就解决了,找到最优的 v π ∗ = m a x π v ( s ) v_{\pi}^* = max_{\pi}v(s) vπ∗=maxπv(s)就行了。
那该怎么求解 v π ∗ v_{\pi}^* vπ∗呢?
相关文章:

暴力快速入门强化学习
强化学习算法的基本思想(直觉) 众所周知,强化学习是能让智能体实现某个具体任务的强大算法。 强化学习的基本思想是让智能体跟环境交互,通过环境的反馈让智能体调整自己的策略,从反馈中学习,不断学习来得到…...

vue中v-if和v-show的区别
手段:v-if是动态的向DOM树内添加或者删除DOM元素;v-show是通过设置DOM元素的display样式属性控制显隐;编译过程:v-if切换有一个局部编译/卸载的过程,切换过程中合适地销毁和重建内部的事件监听和子组件;v-s…...
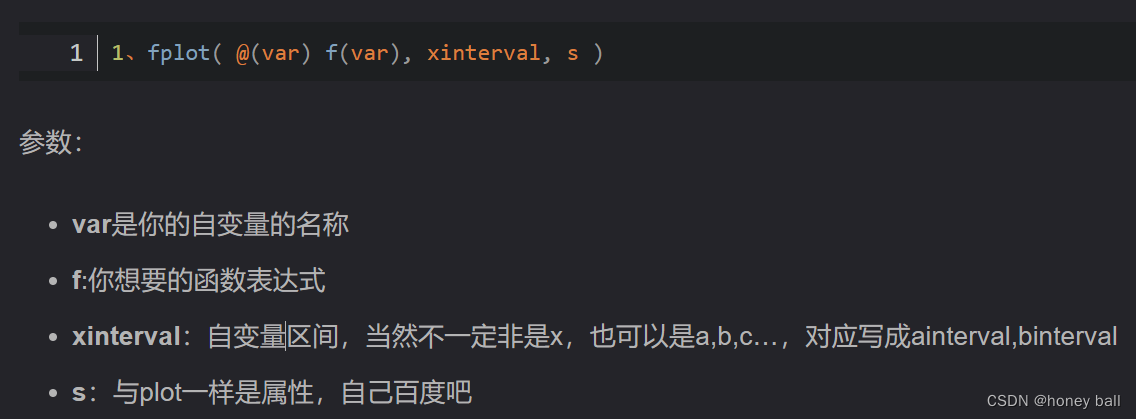
MATLAB绘图
现学现用,用时再学。 plot函数:有两个向量被指定为参数,plot(x,y) 会生成 y 对 x 的图形 添加轴标签和标题: 通过调用一次 plot,多个 x-y 对组参数会创建多幅图形: 在每十个数据点处放置标记: 一个窗口绘制多个图形; 可在弹窗的插入选项上添加…...

嵌入式学习-ARM-Day4
嵌入式学习-ARM-Day4 实现三个LED灯亮灭 .text .global _start _start: 使能GPIOE的外设时钟 RCC_MP_AHB4ENSETR的第[4]设置为1即可使能GPIOE时钟 LED1 LDR R0,0X50000A28 指定寄存器地址 LDR R1,[R0] 将寄存器原来的数值读取出来,保存到R1中 ORR R1,R1,#(0x…...

MySQL 中的事务和存储引擎
目录 事务的 ACID 特性 MySQL 的四种隔离机制和问题 MySQL 的四种隔离机制: MySQL 的存储引擎 InnoDB 存储引擎 MyISAM 存储引擎 Memory 存储引擎 通过 ALTER TABLE 语句更改存储引擎 在创建表时指定存储引擎 通过修改配置文件设置默认存储引擎 在数据库系…...
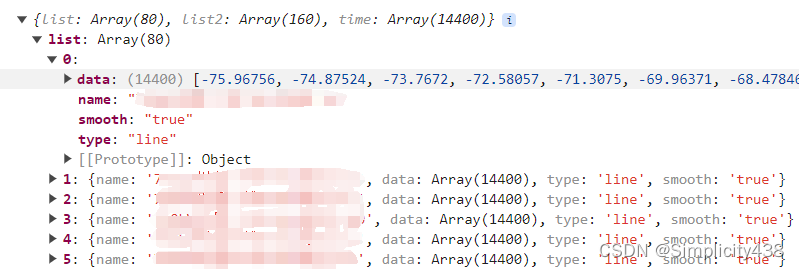
echarts多个折线图共用一个x轴和tooltip组件
实现效果 根据接口传来的数据,使用echarts绘制出,共用一个x轴的图表 功能:后端将所有数据传送过来,前端通过监听选中值来展示对应的图表数据 数据格式: 代码: <template><div><div clas…...

wireshark数据捕获实验简述
Wireshark是一款开源的网络协议分析工具,它可以用于捕获和分析网络数据包。是一款很受欢迎的“网络显微镜”。 实验拓扑图: 实验基础配置: 服务器: ip:172.16.1.88 mask:255.255.255.0 r1: sys sysname r1 undo info enable in…...

如何利用RunnerGo简化性能测试流程
在软件开发过程中,测试是一个重要的环节,需要投入大量时间和精力来确保应用程序或网站的质量和稳定性。但是,随着应用程序变得更加复杂和庞大,传统的测试工具在面对比较繁琐的项目时非常费时费力。这时,一些自动化测试…...

继承和深拷贝封装
继承和深拷贝封装 今日目标: 1.es5寄生组合式继承 2.es6类的继承 3.深拷贝函数封装 00-回顾 # 不同数据类型赋值时的区别: 基本数据类型,赋的就是值,相互之间不再有任何影响 引用数据类型,赋的是地址,…...
《定时执行专家》:Nircmd 的超级搭档,解锁自动化新境界
目录 Nircmd 简介 《定时执行专家》与 Nircmd 的结合 示例: 自动清理电脑垃圾: 定时发送邮件: 定时关闭电脑: 《定时执行专家》的优势: 总结: 以下是一些其他使用示例: 立即下载《定时执行专家》: Nircmd 官方网站: 更…...

Android 封装的工具类
文章目录 日志封装类-MyLog线程封装类-LocalThreadPools自定义进度条-LoadProgressbar解压缩类-ZipUtils本地数据库类-MySQLiteHelper访问webservice封装-HttpUtilsToolbar封装类-MaterialToolbar网络请求框架-OkGo网络请求框架-OkHttp 日志封装类-MyLog 是对android log的封装…...
linux下线程分离属性
linux下线程分离属性 一、线程的属性---分离属性二、线程属性设置2.1 线程创建前设置分离属性2.2 线程创建后设置分离属性 一、线程的属性—分离属性 什么是分离属性? 首先分离属性是线程的一个属性,有了分离属性的线程,不需要别的线程去接合…...

Leetcode 208. 实现 Trie (前缀树)
心路历程: 一道题干进去了一个下午,单纯从解题角度可以直接用python的集合就很简单地解决(不知道是不是因为python底层的set()类)。后来从网上看到这道题应该从前缀树的角度去做,于是花了半个多小时基于字典做了前缀树…...
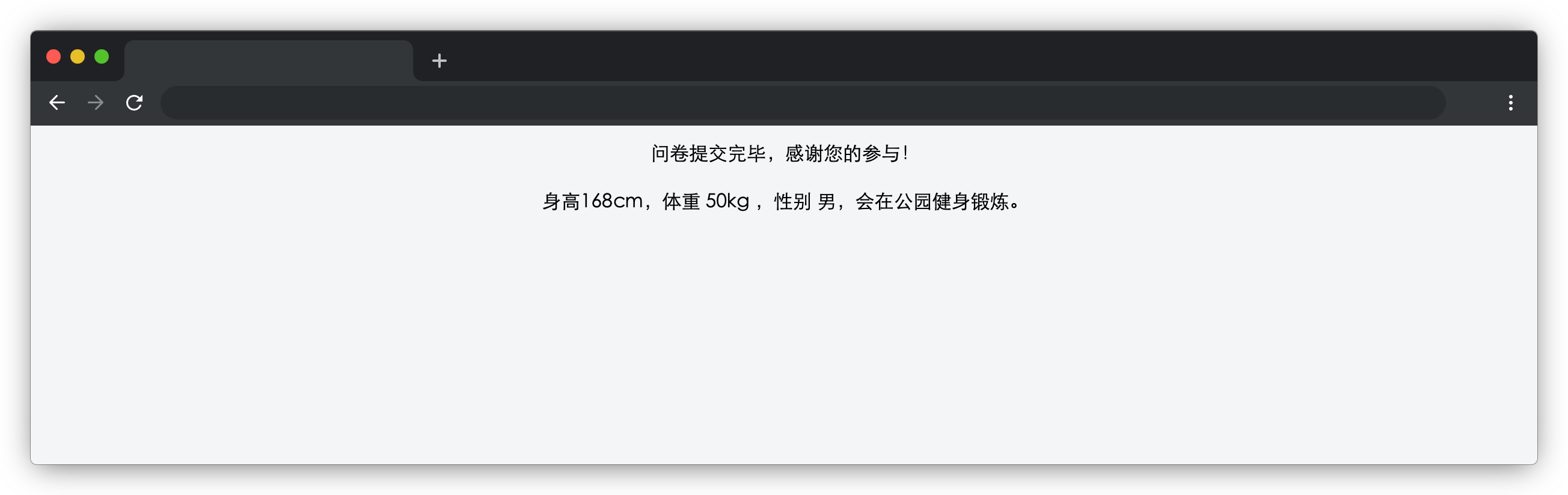
蓝桥杯练习题——健身大调查
在浏览器中预览 index.html 页面效果如下: 目标 完成 js/index.js 中的 formSubmit 函数,用户填写表单信息后,点击蓝色提交按钮,表单项隐藏,页面显示用户提交的表单信息(在 id 为 result 的元素显示&#…...

React——组件通讯
组件通讯介绍 组件中的状态是私有的,组件的状态只能在组件内部使用,无法直接在组件外使用,但是我们在日常开发中,通常会把相似、功能完整的应用才分成组件(工厂模式)利于我们的开发,而不同组件直…...
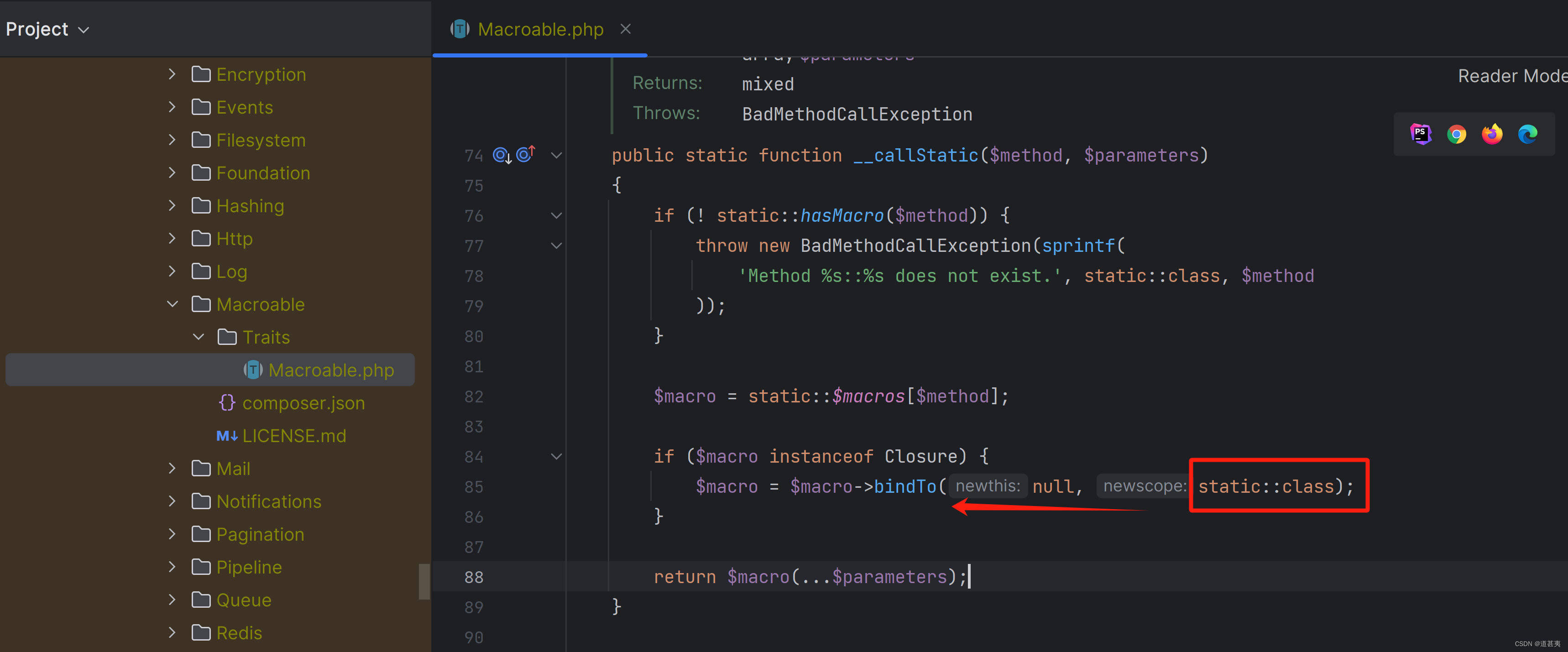
php闭包应用
laravel 路由 bingTo 把路由URL映射到匿名回调函数上,框架会把匿名回调函数绑定到应用对象上,这样在匿名函数中就可以使用$this关键字引用重要的应用对象。Illuminate\Support\Traits\Macroable的__call方法。 自己写一个简单的demo: <?php <?…...

基于python+vue的OA公文发文管理系统flask-django-php-nodejs
系统根据现有的管理模块进行开发和扩展,采用面向对象的开发的思想和结构化的开发方法对OA公文发文管理的现状进行系统调查。采用结构化的分析设计,该方法要求结合一定的图表,在模块化的基础上进行系统的开发工作。在设计中采用“自下而上”的…...

脉冲变压器电感的工艺结构原理及选型参数总结
🏡《总目录》 目录 1,概述2,工作原理3,结构特点3.1,铁心结构3.2,铁心材料3.3,绕组4,工艺流程4.1,准备铁芯4.2,绕制线圈4.3,安装线圈4.4,固定线圈4.5,绝缘处理4.6,高压脉冲引出...

java中Arrays介绍及常用方法
在Java中,java.util.Arrays类是一个提供了各种操作数组的工具类。该类提供了一系列静态方法来对数组进行排序、搜索、填充、复制等操作。下面是对Arrays类的介绍以及常用方法的说明: toString()方法:将数组转换为字符串形式并返回,方便输出数…...

CTF题型 Http请求走私总结Burp靶场例题
CTF题型 Http请求走私总结&靶场例题 文章目录 CTF题型 Http请求走私总结&靶场例题HTTP请求走私HTTP请求走私漏洞原理分析为什么用前端服务器漏洞原理界定标准界定长度 重要!!!实验环境前提POST数据包结构必要结构快速判断Http请求走私类型时间延迟CL-TETE-CL 练习例题C…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
