动态规划15 | ● 392.判断子序列 ● *115.不同的子序列
392.判断子序列
https://programmercarl.com/0392.%E5%88%A4%E6%96%AD%E5%AD%90%E5%BA%8F%E5%88%97.html
- 考点
- 子序列问题
- 我的思路
- dp[i][j]的含义是,两个序列分别取到下标为i和j的时候,他们是否满足前者是后者的子序列,满足为True,否则为False
- 递推公式,分为后者序列取到第j - 1个元素时就已经满足前者序列为其子序列的情况、dp[i - 1][j - 1]满足子序列要求且前者序列的第i个元素和后者序列的第j个元素恰好相等的情况、以及dp[i][j]不满足为子序列的情况
- 初始化,建议画出二维矩阵,并举一个例子来分析,仅额外初始化后者序列对应的第一条边即可(将所有满足子序列要求的位置设置为True),其与都为False
- 视频讲解关键点总结
- 和我的思路不太一样
- 我的思路的问题
- 无
- 代码书写问题
- 无
- 可执行代码
class Solution:def isSubsequence(self, s: str, t: str) -> bool:if s == '':return Trueelif t == '':return Falsedp = [[False] * len(t) for _ in range(len(s))]for i in range(len(t)):if t[i] == s[0]:for j in range(i, len(t)):dp[0][j] = Truebreakfor i in range(1, len(s)):for j in range(1, len(t)):if dp[i][j - 1]:dp[i][j] = Trueelif s[i] == t[j] and dp[i - 1][j - 1]:dp[i][j] = Truereturn dp[-1][-1]
*115.不同的子序列
https://programmercarl.com/0115.%E4%B8%8D%E5%90%8C%E7%9A%84%E5%AD%90%E5%BA%8F%E5%88%97.html
- 考点
- 子序列问题
- 我的思路
- 无思路
- 视频讲解关键点总结
- 明确本题的目标,我们是要在后者元素中删除元素获得子序列来让该子序列与前者序列相同
- dp[i][j]的含义是,两个序列分别取到下标为i和j的时候,后者序列能组合出多少种和前者序列相同的子序列
- 递推公式,如果当前下标的元素相同,则可以同时取当前下标元素(此时dp[i][j] = dp[i - 1][j - 1])或者不取后者序列的当前元素(此时dp[i][j] = dp[i][j - 1]);如果当前下标的元素不相同,则只有dp[i][j] = dp[i][j - 1]
- 初始化,建议画出二维矩阵,并举一个例子来分析,仅额外初始化后者序列对应的第一条边即可
- 我的思路的问题
- 无思路
- 代码书写问题
- 无
- 可执行代码
class Solution:def numDistinct(self, s: str, t: str) -> int:dp = [[0] * len(s) for _ in range(len(t))]if s[0] == t[0]:dp[0][0] = 1for i in range(1, len(s)):if t[0] == s[i]:dp[0][i] = dp[0][i - 1] + 1else:dp[0][i] = dp[0][i - 1]for i in range(1, len(t)):for j in range(1, len(s)):if s[j] == t[i]:dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1]else:dp[i][j] = dp[i][j - 1]return dp[-1][-1]
相关文章:

动态规划15 | ● 392.判断子序列 ● *115.不同的子序列
392.判断子序列 https://programmercarl.com/0392.%E5%88%A4%E6%96%AD%E5%AD%90%E5%BA%8F%E5%88%97.html 考点 子序列问题 我的思路 dp[i][j]的含义是,两个序列分别取到下标为i和j的时候,他们是否满足前者是后者的子序列,满足为True&#x…...

APP UI自动化测试思路总结
首先想要说明一下,APP自动化测试可能很多公司不用,但也是大部分自动化测试工程师、高级测试工程师岗位招聘信息上要求的,所以为了更好的待遇,我们还是需要花时间去掌握的,毕竟谁也不会跟钱过不去。 接下来,…...
)
Codeforces Round 936 (Div. 2)
C. Tree Cutting 题意:给定一棵树,需要删除 k 条边,使得 k1 个联通块中的最小结点数最大。求出这个最大值 思路:求最小值最大--想到二分答案--然后深搜满足条件的连通块是否大于k即可 #include<iostream> #include<al…...
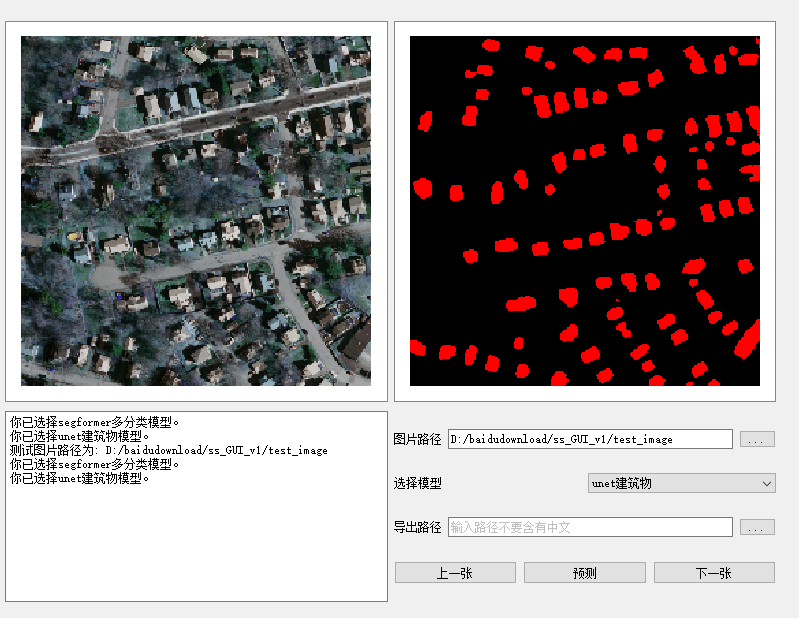
yolov6实现遥感影像目标识别|以DIOR数据集为例
1 目标检测是计算机视觉领域中的一项重要任务,它的目标是在图像或视频中检测出物体的位置和类别。YOLO(You Only Look Once)是一系列经典的目标检测算法,最初由Joseph Redmon等人于2016年提出。YOLO算法具有快速、简单、端到端的特…...

stable-diffusion-electron-clickstart 支持windows AMD显卡
前言 使用vue3 vite electron element-plus构建,正好学习下electrongithub stable-diffusion “画境导航者” 启动器 简介 stable-diffusion “画境导航者” 启动器支持功能 一键启动打开文件夹(tmp、txt2img-images)等模型所在文件夹&…...

ES进程除了kill之外,有什么优雅关闭的方式吗?
问题 Linux环境中,Elasticsearch 8的进程除了kill之外,有什么优雅关闭的方式吗? 具体实施方式 在Linux环境中,Elasticsearch(ES)进程可以通过多种方式实现优雅关闭,这种方式允许它完成必要的…...
院子摄像头的监控
院子摄像头的监控和禁止区域入侵检测相比,多了2个功能:1)如果检测到有人入侵,则把截图保存起来,2)如果检测到有人入侵,则向数据库插入一条事件数据。 打开checkingfence.py,添加如下…...

SpringBoot3使用响应Result类返回的响应状态码为406
Resolved [org.springframework.web.HttpMediaTypeNotAcceptableException: No acceptable representation] 解决方法:Result类上加上Data注解...
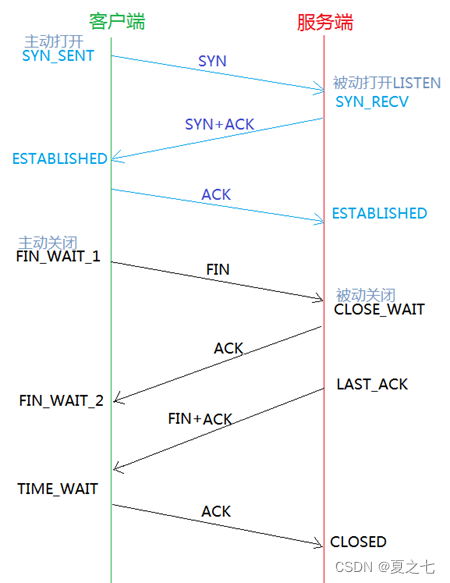
基础:TCP四次挥手做了什么,为什么要挥手?
1. TCP 四次挥手在做些什么 1. 第一次挥手 : 1)挥手作用:主机1发送指令告诉主机2,我没有数据发送给你了。 2)数据处理:主机1(可以是客户端,也可以是服务端),…...

Android Studio实现内容丰富的安卓校园二手交易平台(带聊天功能)
获取源码请点击文章末尾QQ名片联系,源码不免费,尊重创作,尊重劳动 项目编号083 1.开发环境android stuido jdk1.8 eclipse mysql tomcat 2.功能介绍 安卓端: 1.注册登录 2.查看二手商品列表 3.发布二手商品 4.商品详情 5.聊天功能…...

第十一届蓝桥杯省赛第一场真题
2065. 整除序列 - AcWing题库 #include <bits/stdc.h> using namespace std; #define int long long//记得开long long void solve(){int n;cin>>n;while(n){cout<<n<< ;n/2;} } signed main(){int t1;while(t--)solve();return 0; } 2066. 解码 - …...
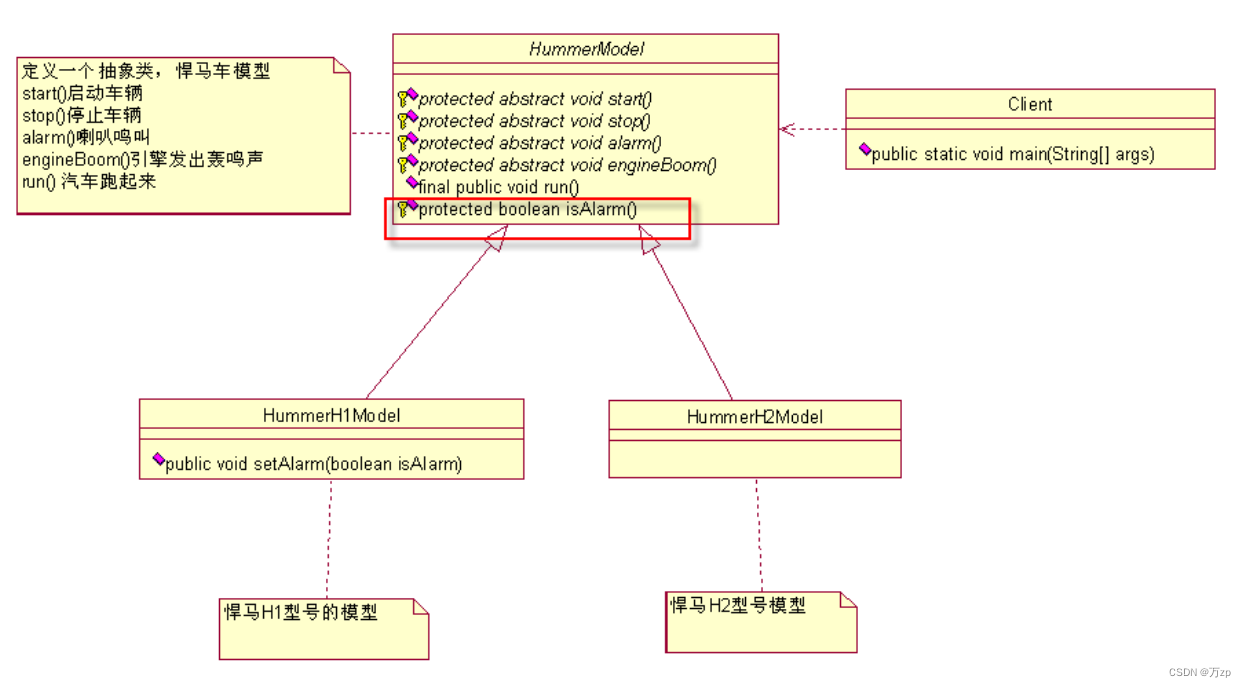
设计模式 模板方法模式
01.如果接到一个任务,要求设计不同型号的悍马车 02.设计一个悍马车的抽象类(模具,车模) public abstract class HummerModel {/** 首先,这个模型要能够被发动起来,别管是手摇发动,还是电力发动…...
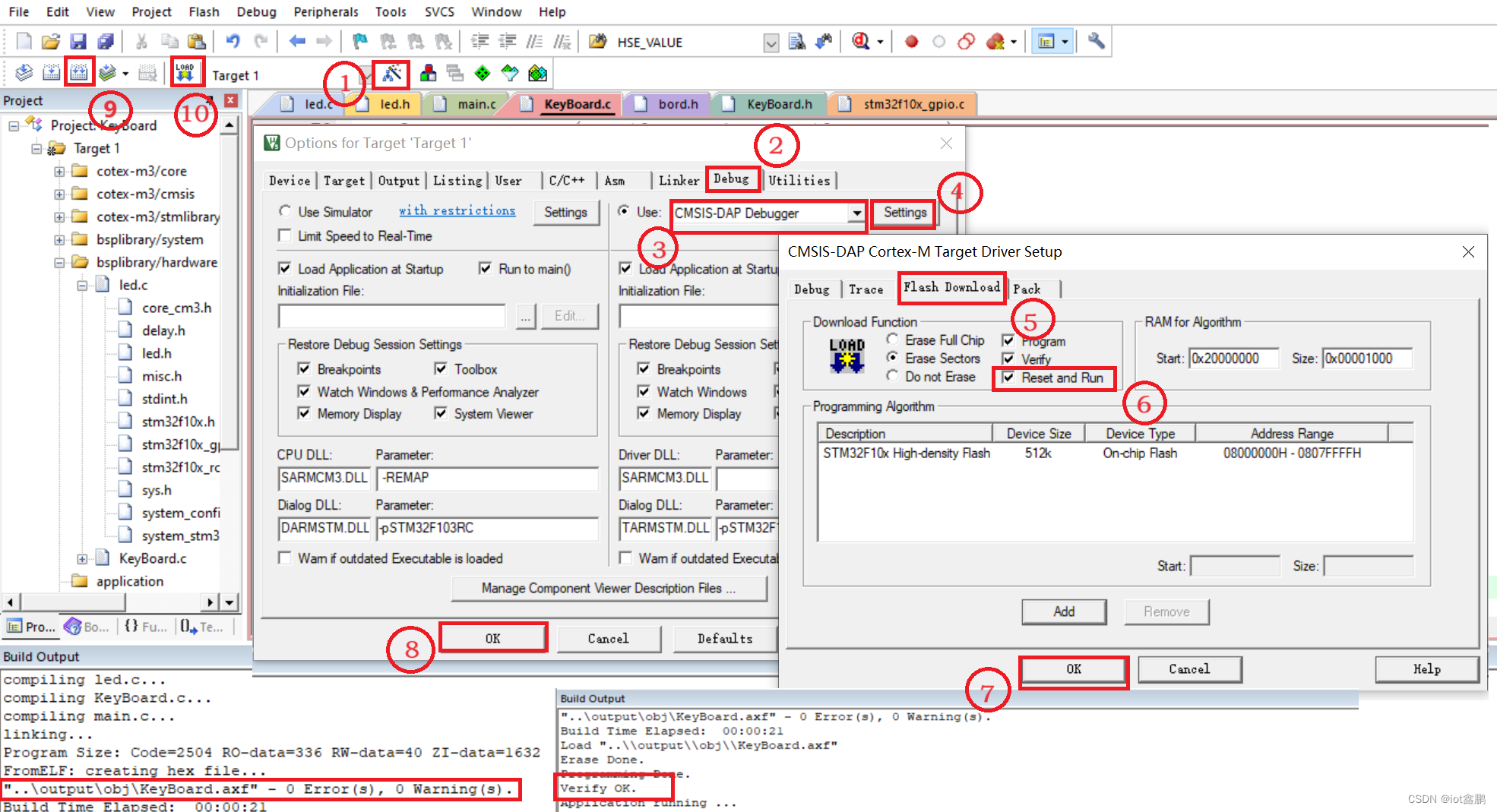
【STM32嵌入式系统设计与开发】——6矩阵按键应用(4x4)
这里写目录标题 一、任务描述二、任务实施1、SingleKey工程文件夹创建2、函数编辑(1)主函数编辑(2)LED IO初始化函数(LED_Init())(3)开发板矩阵键盘IO初始化(ExpKeyBordInit())&…...

乐优商城(九)数据同步RabbitMQ
1. 项目问题分析 现在项目中有三个独立的微服务: 商品微服务:原始数据保存在 MySQL 中,从 MySQL 中增删改查商品数据。搜索微服务:原始数据保存在 ES 的索引库中,从 ES 中查询商品数据。商品详情微服务:做…...
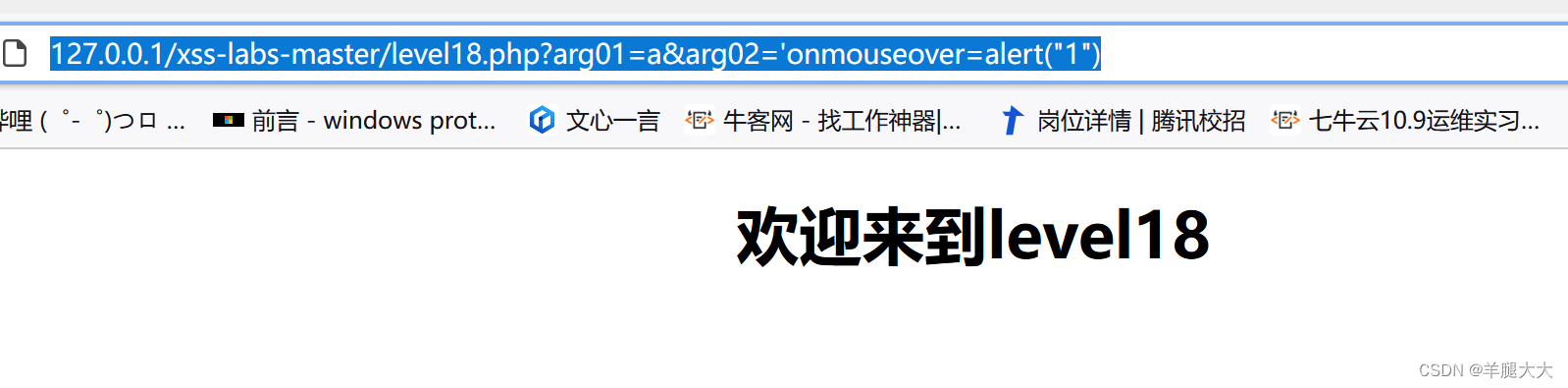
XSS-labs详解
xss-labs下载地址https://github.com/do0dl3/xss-labs 进入靶场点击图片,开始我们的XSS之旅! Less-1 查看源码 代码从 URL 的 GET 参数中取得 "name" 的值,然后输出一个居中的标题,内容是 "欢迎用户" 后面…...

设计模式——模板方法模式封装.net Core读取不同类型的文件
1、模板方法模式 模板方法模式:定义一个操作中的算法骨架,而将一些步骤延迟到子类中,模板方法使得子类可以不改变一个算法的结构即可重定义该算法的某些特定步骤。 特点:通过把不变的行为搬移到超类,去除子类中重复的代…...

[思考记录]技术欠账
最近对某开发项目做回顾梳理,除了进一步思考整理相关概念和问题外,一个重要的任务就是清理“技术欠账”。 这个“技术欠账”是指在这个项目的初期,会有意无意偏向快速实现,想先做出来、用起来,进而在实现过程中做出…...

React - 实现菜单栏滚动
简介 本文将会基于react实现滚动菜单栏功能。 技术实现 实现效果 点击菜单,内容区域会自动滚动到对应卡片。内容区域滑动,指定菜单栏会被选中。 ScrollMenu.js import {useRef, useState} from "react"; import ./ScrollMenu.css;export co…...
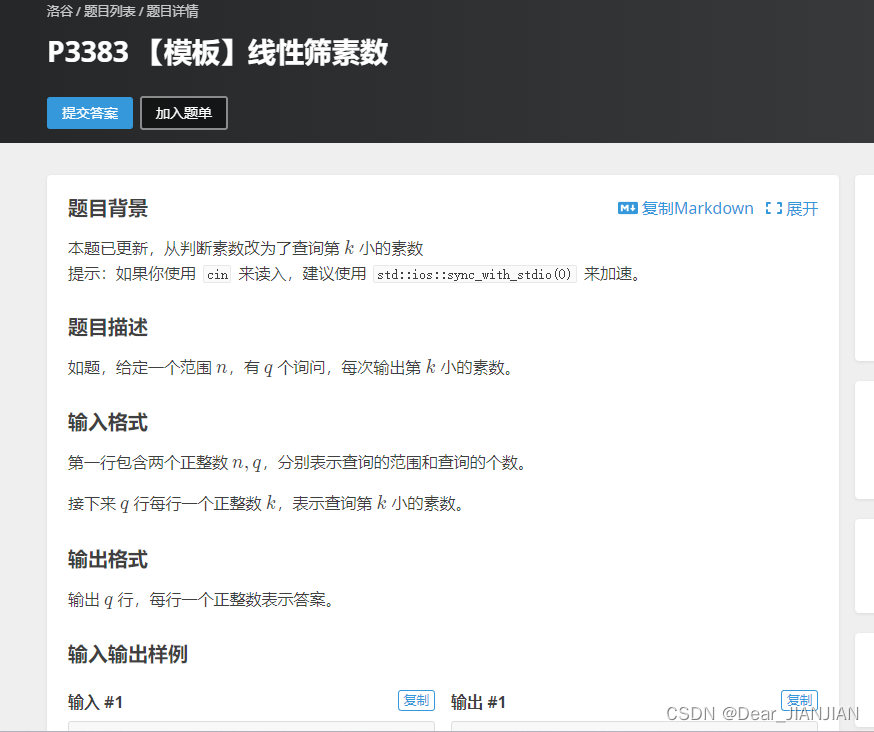
线性筛选(欧拉筛选)-洛谷P3383
#include <bits/stdc.h> using namespace std; int main() {std::ios::sync_with_stdio(false); cin.tie(nullptr); //为了加速int n, q;cin >> n >> q; vector<int>num(n 1); //定义数字表vector<int>prime; //定义素数表数组num[1] …...
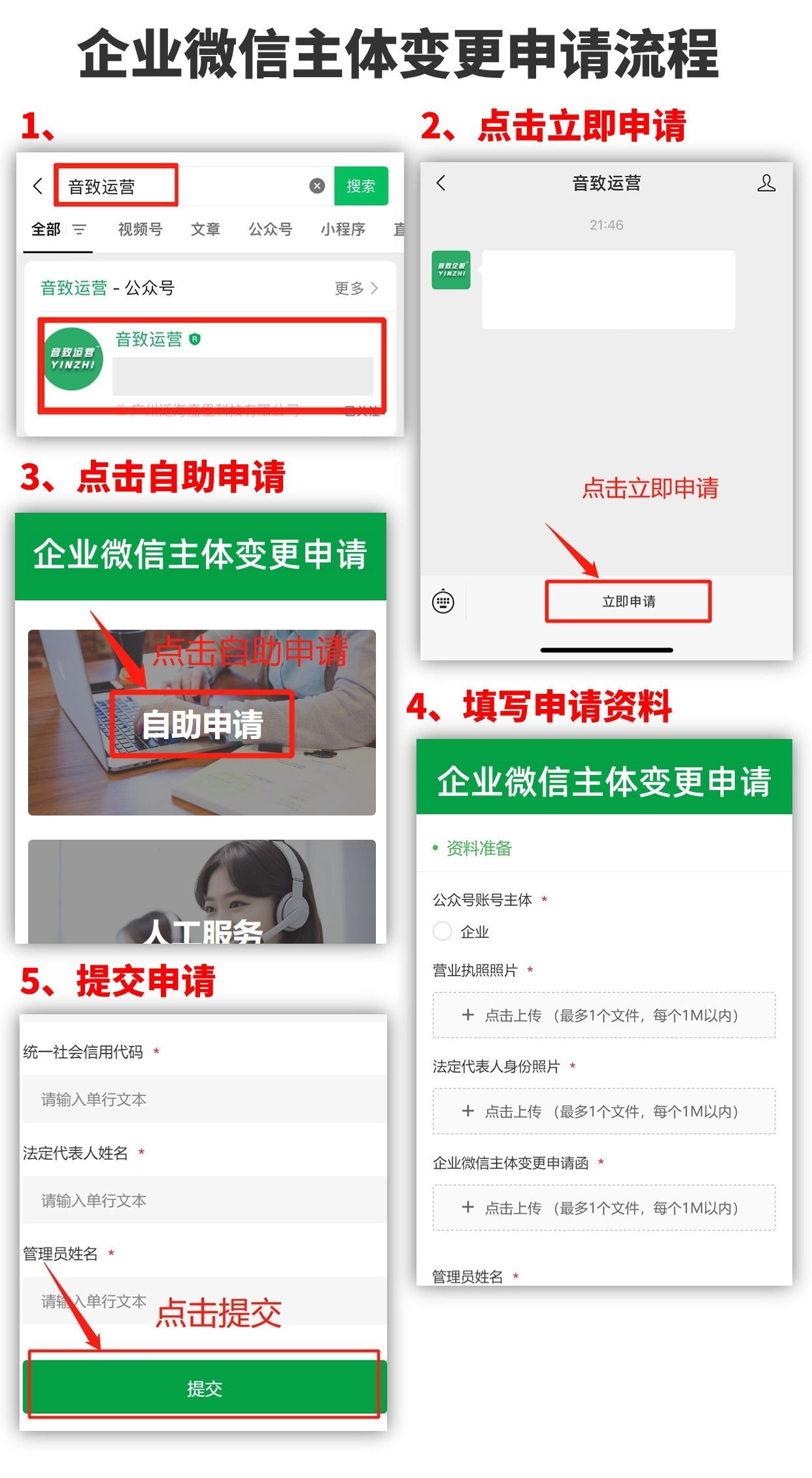
企业微信可以更换公司主体吗?
企业微信变更主体有什么作用?当我们的企业因为各种原因需要注销或已经注销,或者运营变更等情况,企业微信无法继续使用原主体继续使用时,可以申请企业主体变更,变更为新的主体。企业微信变更主体的条件有哪些࿱…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
