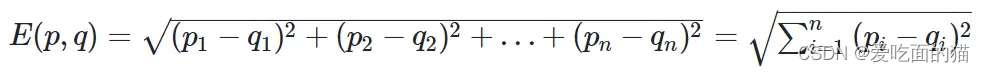常用相似度计算方法总总结
一、欧几里得相似度
1、欧几里得相似度
公式如下所示:
 2、自定义代码实现
2、自定义代码实现
import numpy as np
def EuclideanDistance(x, y):import numpy as npx = np.array(x)y = np.array(y)return np.sqrt(np.sum(np.square(x-y)))# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])euclidean_distance = EuclideanDistance(x, y)
print(f"euclidean distance is: {euclidean_distance}")二、皮尔森相关性系数
1、皮尔森相关性系数
相关系数:考察两个事物(在数据里我们称之为变量)之间的相关程度。
公式如下所示:
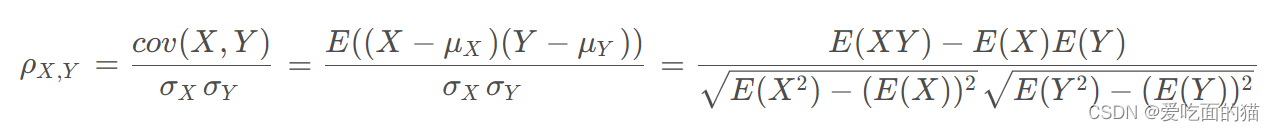

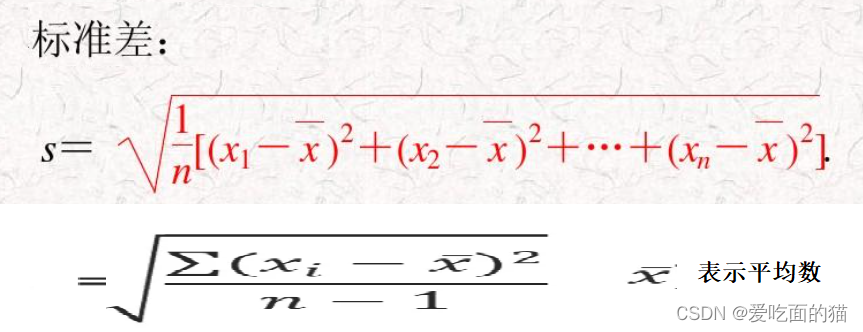
如果有两个变量:X、Y,最终计算出的相关系数的含义可以有如下理解:
(1)、当相关系数为0时,X和Y两变量无关系。
(2)、当X的值增大(减小),Y值增大(减小),两个变量为正相关,相关系数在0.00与1.00之间。
(3)、当X的值增大(减小),Y值减小(增大),两个变量为负相关,相关系数在-1.00与0.00之间。
相关系数的绝对值越大,相关性越强,相关系数越接近于1或-1,相关度越强,相关系数越接近于0,相关度越弱。
通常情况下通过以下取值范围判断变量的相关强度:
相关系数 0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关
2、代码实现过程
自定义实现过程
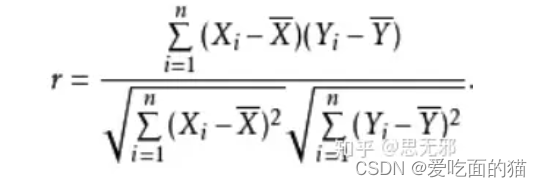
import numpy as npdef pearson_correlation(x, y):n = len(x)# 计算平均值x_bar = np.sum(x) / n
# y_bar = np.sum(y) / n# 计算协方差cov_xy = np.sum((x - x_bar) * (y - y_bar))# 计算标准差std_dev_x = np.sqrt(np.sum((x - x_bar) ** 2) / (n - 1))std_dev_y = np.sqrt(np.sum((y - y_bar) ** 2) / (n - 1))# 计算皮尔逊相似系数r = cov_xy / (std_dev_x * std_dev_y)return r# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])# 计算皮尔逊相似系数
pearson_coefficient = pearson_correlation(x, y)
print(f"Pearson correlation coefficient: {pearson_coefficient}")numpy中的corrcpef()封装实现
import numpy as np# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]x=np.array([3.3,6.5,2.8,3.4,5.5])
y=np.array([3.5,5.8,3.1,3.6,5.1])pc=np.corrcoef(x,y)print(pc)3、适用范围
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
(1)、两个变量之间是线性关系,都是连续数据。
(2)、两个变量的总体是正态分布,或接近正态的单峰分布。
(3)、两个变量的观测值是成对的,每对观测值之间相互独立。
三、余弦相似度
1、余弦相似度
公式如下所示:
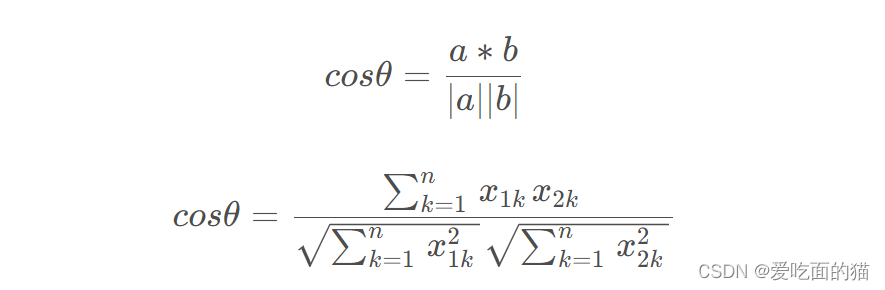
2、自定义代码实现
import numpy as np
def moreCos(a,b):sum_fenzi = 0.0sum_fenmu_1,sum_fenmu_2 = 0,0for i in range(len(a)):sum_fenzi += a[i]*b[i]sum_fenmu_1 += a[i]**2sum_fenmu_2 += b[i]**2return sum_fenzi/(np.sqrt(sum_fenmu_1) * np.sqrt(sum_fenmu_2) )# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])cos = moreCos(x, y)
print(f"cos is: {cos}")四、曼哈顿相似度
1、曼哈顿相似度
公式如下所示:
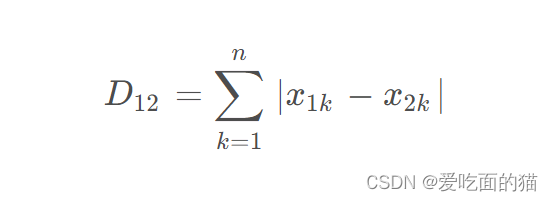
2、自定义代码实现
import numpy as np
def ManhattanDistance(x, y):import numpy as npx = np.array(x)y = np.array(y)return np.sum(np.abs(x-y))# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])manhattan_distance = ManhattanDistance(x, y)
print(f"manhattan distance is: {manhattan_distance}")五、切比雪夫距离
1、切比雪夫距离
公式如下所示:
切比雪夫距离(Chebyshev Distance)的定义为:max( | x2-x1 | , |y2-y1 | , … ), 切比雪夫距离用的时候数据的维度必须是三个以上。
2、自定义代码实现
import numpy as np
def ChebyshevDistance(x, y):import numpy as npx = np.array(x)y = np.array(y)return np.max(np.abs(x-y))# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])chebyshev_istance = ChebyshevDistance(x, y)
print(f"manhattan distance is: {chebyshev_istance}")六、马氏距离
1、马氏距离
公式如下所示:
M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到u的马氏距离表示为
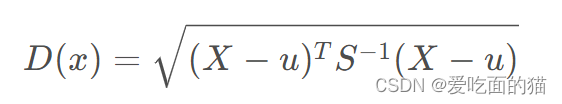
2、自定义代码实现
def MahalanobisDistance(x, y):'''马氏居立中的(x,y)与欧几里得距离的(x,y)不同,欧几里得距离中的(x,y)指2个样本,每个样本的维数为x或y的维数;这里的(x,y)指向量是2维的,样本个数为x或y的维数,若要计算n维变量间的马氏距离则需要改变输入的参数如(x,y,z)为3维变量。'''import numpy as npx = np.array(x)y = np.array(y)X = np.vstack([x, y])X_T = X.Tsigma = np.cov(X)sigma_inverse = np.linalg.inv(sigma)d1 = []for i in range(0, X_T.shape[0]):for j in range(i + 1, X_T.shape[0]):delta = X_T[i] - X_T[j]d = np.sqrt(np.dot(np.dot(delta, sigma_inverse), delta.T))d1.append(d)return d1# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])mahalanobis_istance = MahalanobisDistance(x, y)
print(f"mahalanobis distance is: {mahalanobis_istance}")七、闵可夫斯基距离
1、闵可夫斯基距离
公式如下所示:
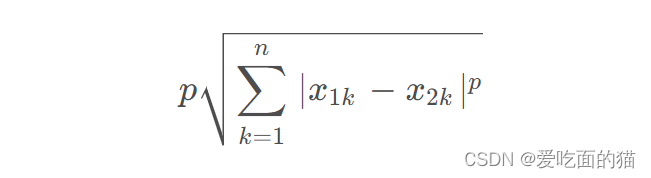
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
2、自定义代码实现
import numpy as npdef MinkowskiDistance(x, y, p):import mathimport numpy as npzipped_coordinate = zip(x, y)return math.pow(np.sum([math.pow(np.abs(i[0] - i[1]), p) for i in zipped_coordinate]), 1 / p)# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3, 6.5, 2.8, 3.4, 5.5])
y = np.array([3.5, 5.8, 3.1, 3.6, 5.1])# minkowski_istance = MinkowskiDistance(x, y,1)
# minkowski_istance = MinkowskiDistance(x, y,2)
minkowski_istance = MinkowskiDistance(x, y,3)
print(f"minkowski_ distance is: {minkowski_istance}")
八、信息熵
1、 信息熵
衡量分布的混乱程度或分散程度的一种度量.
熵的值就越大,样本一致性越低,越代表分之样本种类越多,越混乱,不确定性越强。
熵的值就越小,样本一致性越高,样本越倾向于某一类。
熵的值就为0,代表样本完全属于同一类。
公式如下所示:
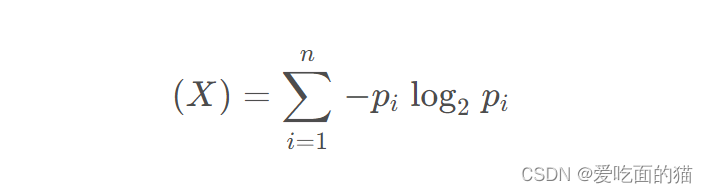
2、自定义代码实现
import numpy as np# 示例数据data=np.array(['a','b','c','a','a','b'])data1=np.array(['中国','中国','中国','中国','中国','中国','中国','中国','人民',])#计算信息熵的方法
def calc_ent(x):"""calculate shanno ent of x"""x_value_list = set([x[i] for i in range(x.shape[0])])ent = 0.0for x_value in x_value_list:p = float(x[x == x_value].shape[0]) / x.shape[0]logp = np.log2(p)ent -= p * logpreturn entent = calc_ent(data)
ent1= calc_ent(data1)print(f"ent is: {ent}")
print(f"ent is: {ent1}")相关文章:
常用相似度计算方法总总结
一、欧几里得相似度 1、欧几里得相似度 公式如下所示: 2、自定义代码实现 import numpy as np def EuclideanDistance(x, y):import numpy as npx np.array(x)y np.array(y)return np.sqrt(np.sum(np.square(x-y)))# 示例数据 # 用户1 的A B C D E商品数据 [3.3…...
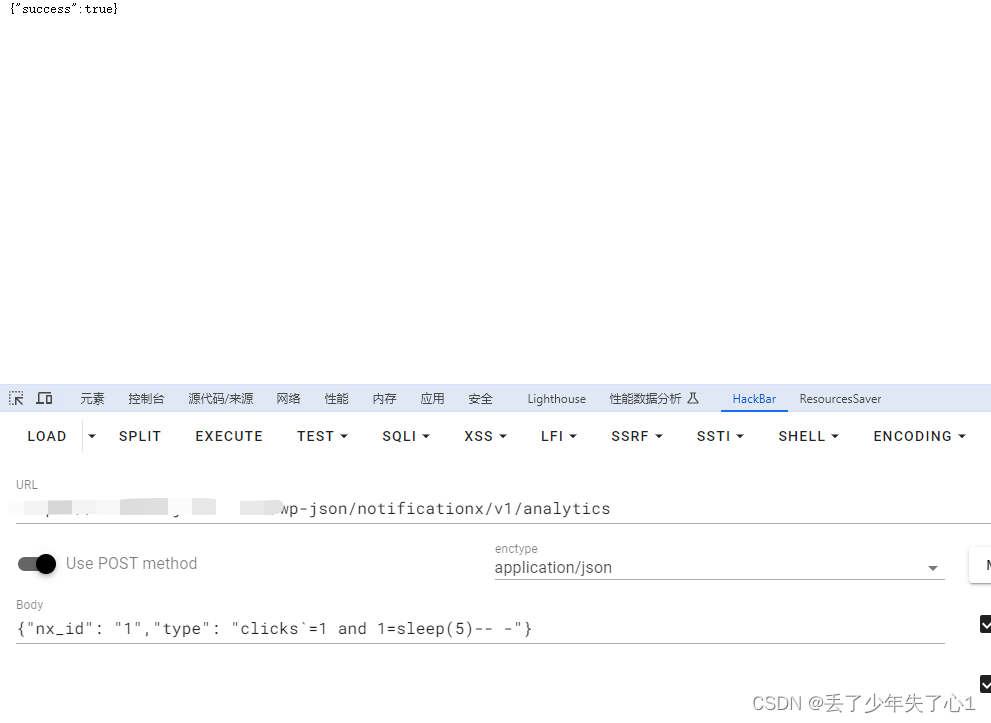
【漏洞复现】WordPress Plugin NotificationX 存在sql注入CVE-2024-1698
漏洞描述 WordPress和WordPress plugin都是WordPress基金会的产品。WordPress是一套使用PHP语言开发的博客平台。该平台支持在PHP和MySQL的服务器上架设个人博客网站。WordPress plugin是一个应用插件。 WordPress Plugin NotificationX 存在安全漏洞,该漏洞源于对用户提供的…...
AI新工具(20240322) 免费试用Gemini Pro 1.5;先进的AI软件工程师Devika;人形机器人Apptronik给你打果汁
✨ 1: Gemini Pro 1.5 免费试用Gemini Pro 1.5 Gemini 1.5 Pro是Gemini系列模型的最新版本,是一种计算高效的多模态混合专家(MoE)模型。它能够从数百万个上下文Token中提取和推理细粒度信息,包括多个长文档和数小时的视频、音频…...
)
鬼灭之刃-激情台词-02(解释来自文心一言)
愤怒吧,不共戴天的仇恨,强悍而纯粹的愤怒,将会化作坚不可摧的原动力,督促你变强 —— 吾峠呼世晴《鬼灭之刃》 愤怒和仇恨是一种强烈的情感,它们可以驱使人们去寻求改变,去变得更加强大。在故事中ÿ…...

openssl3.2 - exp - aes-128-cbc
文章目录 openssl3.2 - exp - aes-128-cbc概述笔记openssl 命令行实现简单直白的实现简单直白的实现 - 测试效果简单直白的实现 - 测试工程 周全灵活的实现周全灵活的实现 - 测试效果周全灵活的实现 - 测试工程 清晰一些的版本END openssl3.2 - exp - aes-128-cbc 概述 想将工…...
基于docker+rancher部署Vue项目的教程
基于dockerrancher部署Vue的教程 前段时间总有前端开发问我Vue如何通过docker生成镜像,并用rancher上进行部署?今天抽了2个小时研究了一下,给大家记录一下这个过程。该部署教程适用于Vue、Vue2、Vue3等版本。 PS:该教程基于有一定…...

Elasticsearch:让你的 Elasticsearch 索引与 Python 和 Google Cloud Platform 功能保持同步
作者:来自 Elastic Garson Elasticsearch 内的索引 (index) 是你可以将数据存储在文档中的位置。 在使用索引时,如果你使用的是动态数据集,数据可能会很快变旧。 为了避免此问题,你可以创建一个 Python 脚本来更新索引࿰…...

如何定位web前后台的BUG
一、对系统整体的了解 Server端:jspServletjson 数据库:sql、MySQL、oracle等 前台: 涉及到 jstl,jsp,js,css,htm等方面 后台:servlet,jms,ejb࿰…...

谈谈 IOC 和 AOP
我之前面试的时候,真的会有面试官问这个。我感觉确实这个比较高频,因为 Spring 框架最核心的就是这两个东西嘛,掌握了这两个就相当于掌握了 Spring 的半壁江山了。 不过一般面试官不会一上来就问你什么是 AOP 和 IOC,一般都是叫你…...
C/C++之内存旋律:星辰大海的指挥家
个人主页:日刷百题 系列专栏:〖C/C小游戏〗〖Linux〗〖数据结构〗 〖C语言〗 🌎欢迎各位→点赞👍收藏⭐️留言📝 一、C/C内存分布 我们先来了解一下C/C内存分配的几个区域,以下面的代码为例来看…...

Linux下进程的调度与切换
🌎进程的调度与切换 文章目录: 进程的调度与切换 进程切换 进程调度 活动状态进程队列 位图判断 过期队列 总结 前言: 在Linux操作系统中,进程的调度与切换是操作系统核心功能之一ÿ…...
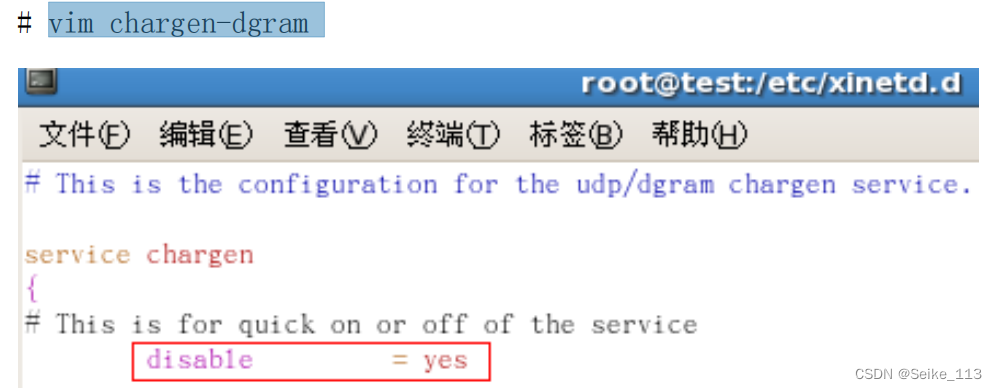
Linux相关命令(2)
1、W :主要是查看当前登录的用户 在上面这个截图里面呢, 第一列 user ,代表登录的用户, 第二列, tty 代表用户登录的终端号,因为在 linux 中并不是只有一个终端的, pts/2 代表是图形界面的第…...
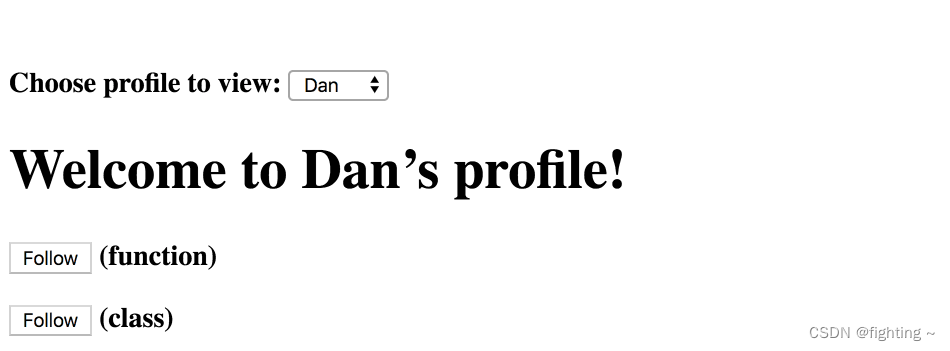
React中 类组件 与 函数组件 的区别
类组件 与 函数组件 的区别 1. 类组件2. 函数组件HookuseStateuseEffectuseCallbackuseMemouseContextuseRef 3. 函数组件与类组件的区别3.1 表面差异3.2 最大不同原因 1. 类组件 在React中,类组件就是基于ES6语法,通过继承 React.component 得到的组件…...

GPT实战系列-智谱GLM-4的模型调用
GPT实战系列-智谱GLM-4的模型调用 GPT专栏文章: GPT实战系列-实战Qwen通义千问在Cuda 1224G部署方案_通义千问 ptuning-CSDN博客 GPT实战系列-ChatGLM3本地部署CUDA111080Ti显卡24G实战方案 GPT实战系列-Baichuan2本地化部署实战方案 GPT实战系列-让CodeGeeX2帮…...

AndroidStudio开发 相关依赖
1、com.google.zxing 用于二维码扫描 2、butterknife 用于简化findView 和 onClick操作 3、pub.devrel:easypermissions 简化权限请求的库 4、 网络请求框架(一):android-async-http 网络请求框架(二):xUtils 网络请求框架(三):Volley Volley…...
)
Zookeeper详解(zk)
文章目录 Zookeeper 概念ZooKeeper的应用场景使用场景zk的原理ZooKeeper、Nacos、Eureka 和 Consul区别Zookeeper的数据结构zk集群脑裂如何解决ZAB 协议假如注册中心挂了,消费者还能调⽤服务吗,用什么调用的dubbo注册中心为什么选择 Zookeeper关于zookee…...

BSD-3-Clause是一种开源软件许可协议
BSD-3-Clause是一种开源软件许可协议,也称为BSD三条款许可证。它是BSD许可证家族中的一种,是一种宽松的许可证,允许软件自由使用、修改和重新分发,同时也保留了一些版权和责任方面的规定。 BSD-3-Clause许可证的主要特点包括以下…...

持续集成平台 02 jenkins plugin 插件
拓展阅读 Devops-01-devops 是什么? Devops-02-Jpom 简而轻的低侵入式在线构建、自动部署、日常运维、项目监控软件 代码质量管理 SonarQube-01-入门介绍 项目管理平台-01-jira 入门介绍 缺陷跟踪管理系统,为针对缺陷管理、任务追踪和项目管理的商业…...

LoadBalancerCacheManager not available, returning delegate without caching
警告:LoadBalancerCacheManager not available, returning delegate without caching 背景:更换了redis集群 解决方案: 重启gateway网关服务 也就是重启引用下面这个包的服务 <dependency><groupId>org.springframework.cloud…...

机器学习金融应用技术指南
1 范围 本文件提供了金融业开展机器学习应用涉及的体系框架、计算资源、数据资源、机器学习引擎、机 器学习服务、安全管理、内控管理等方面的建议。 本文件适用于开展机器学习金融应用的金融机构、技术服务商、第三方安全评估机构等。 2 规范性引用文件 下列文件中的内容通过…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...