RabbitMQ问题
如何实现顺序消费？
消息放入到同一个队列中消费
如何解决消息不丢失？
方案：
如上图：消息丢失有三种情况，解决了以上三种情况就解决了丢失的问题
1、丢失1--->消息在到达交换机的时候；解决：MQ需要开启确认模式
2、丢失2--->在MQ内容丢失的问题；解决：开启消息持久化（交换机设置，队列设置）
3、丢失3--->消息抵达消费者的时候；解决：消费者开始手动ACK
如何解决消费积压？
1、多队列，根据不同消息类型放在不同队列
2、多消费者，根据消息的类型和优先级分配消费者
3、设置TTL，不能无限制阻塞，设置过期时间
如何解决消息重复？
原因：
1、生产者发送消息到MQ，但是由于网络波动，MQ没有回复，生产者又重新发送了一次
2、MQ消息到达消费者时，由于网络波动，没有回复，MQ又重新发送了一次
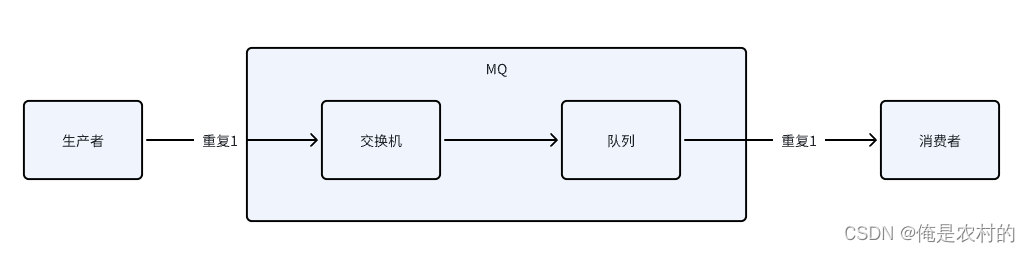
方案：幂等性
1、消息传递时，需要携带一个唯一ID，将此ID存到redis中
2、接收到消息，先去redis中查，如果有则直接丢弃此消息，如果没有正常消费，将该ID存redis设置TTL
相关文章：
RabbitMQ问题
如何实现顺序消费？ 消息放入到同一个队列中消费 如何解决消息不丢失？ 方案： 如上图：消息丢失有三种情况，解决了以上三种情况就解决了丢失的问题 1、丢失1--->消息在到达交换机的时候；解决࿱…...
flutter-＞Scaffold左侧/右侧侧边栏和UserAccountsDrawerHeader的使用
//appBar的 leading/actions 和 Scaffold的drawer/endDrawer 冲突只能存在一个 import package:flutter/material.dart;void main() {runApp(MyApp()); }class MyApp extends StatelessWidget {const MyApp({super.key});overrideWidget build(BuildContext context) {retur…...
vulnhub prime1通关
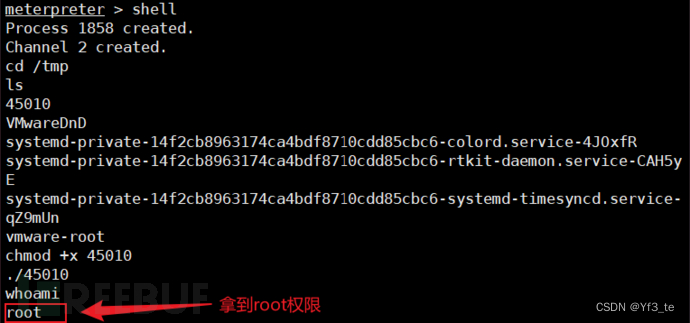
目录 环境安装 1.信息收集 收集IP 端口扫描 目录扫描 目录文件扫描 查找参数 打Boss 远程文件读取 木马文件写入 权限提升 方法一 解锁密钥 方法二： linux内核漏洞提权 总结 环境安装 Kali2021.4及其prime靶机 靶机安装：Prime: 1 ~ Vul…...
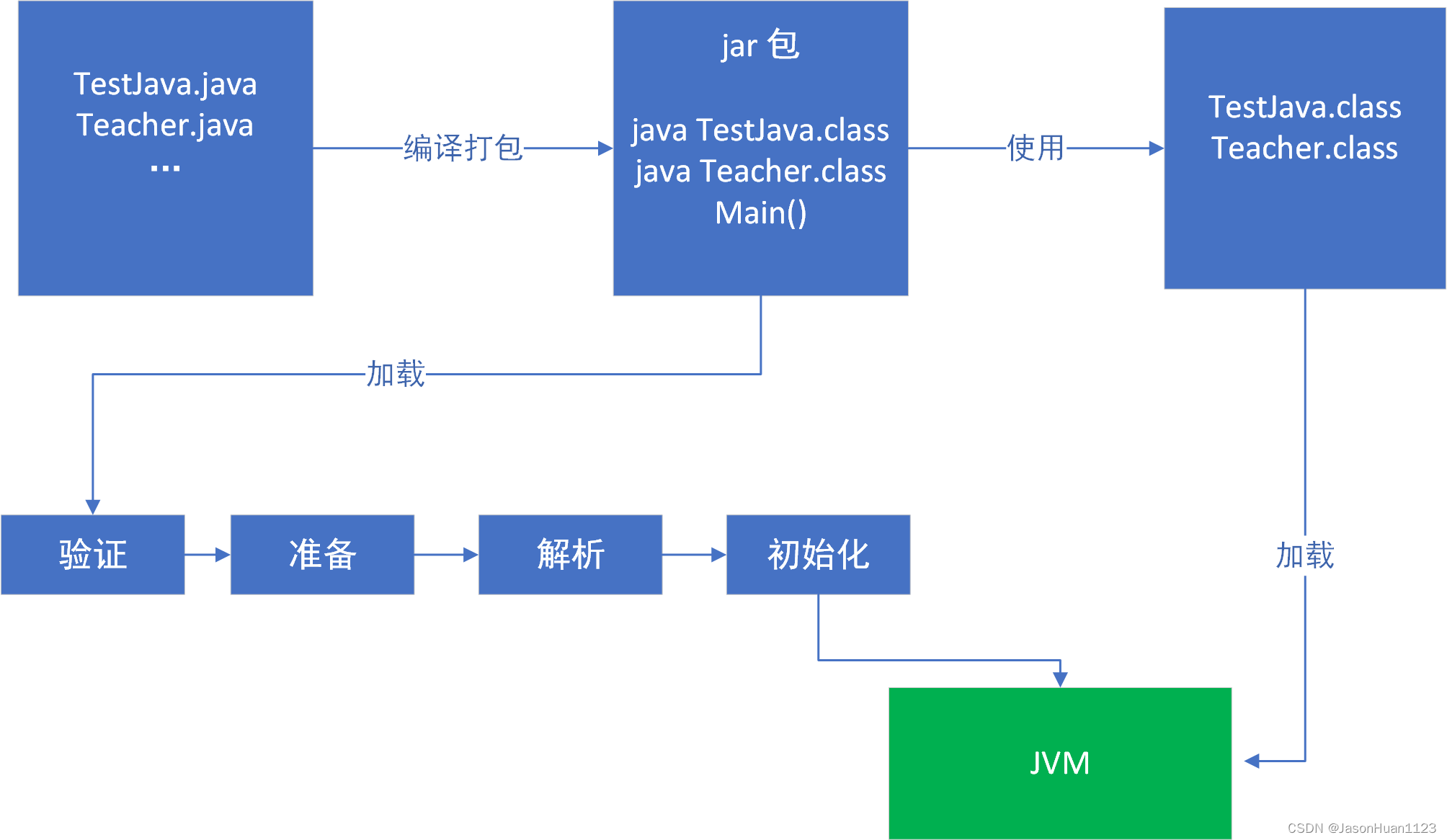
JVM快速入门（1）JVM体系结构、运行时数据区、类加载器、线程共享和独享、分区、Java对象实例化
5.1 JVM体系结构 线程独占区-程序计数器（Program Counter Register） 程序计数器是一块较小的内存空间，它可以看做是当前线程所执行的字节码的行号指示器；在虚拟机的概念模型里，字节码解释器工作时就是通过改变这个计数…...
CSS3新属性（学习笔记）
一、. 圆角 border-radius:; 可以取1-4个值（规则同margin） 可以取px和% 一般用像素，画圆的时候用百分比：border-radius:50%; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8&q…...
41-Vue-webpack基础
webpack基础 前言什么是webpackwebpack的基本使用指定webpack的entry和output 前言 本篇开始来学习下webpack的使用 什么是webpack webpack: 是前端项目工程化的具体解决方案。 主要功能：它提供了友好的前端模块化开发支持，以及代码压缩混淆、处理浏览…...
数据仓库的分层理论
数据仓库的分层理论是为了更好地组织和管理数据，支持复杂的数据分析和决策支持。在这一理论中，数据仓库被分为多个层次，每个层次都有其特定的作用和设计原则。以下是每一层的详细介绍，以及以销售人员为例的Doris建表实例。 ODS层…...
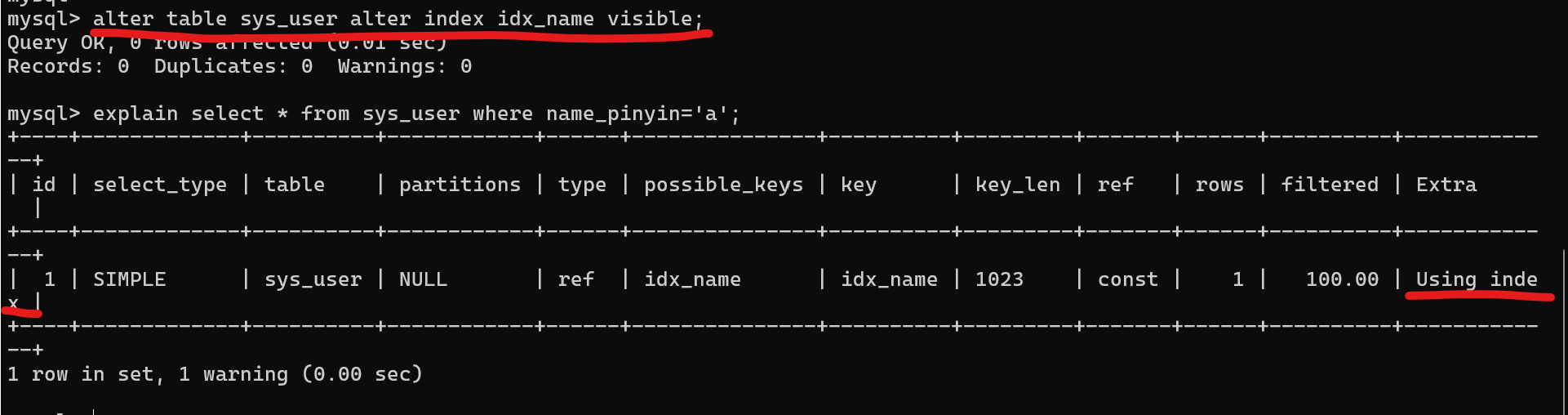
MySQL 8.0-索引- 不可见索引（invisible indexes）
概述 MySQL 8.0引入了不可见索引(invisible index)，这个在实际工作用还是用的到的，我觉得可以了解下。 在介绍不可见索引之前，我先来看下invisible index是个什么或者定义。 我们依然使用拆开来看，然后再把拆出来的词放到MySQL…...
Uibot6.0 (RPA财务机器人师资培训第3天 ）财务招聘信息抓取机器人案例实战
训练网站：泓江科技 (lessonplan.cn)https://laiye.lessonplan.cn/list/ec0f5080-e1de-11ee-a1d8-3f479df4d981https://laiye.lessonplan.cn/list/ec0f5080-e1de-11ee-a1d8-3f479df4d981https://laiye.lessonplan.cn/list/ec0f5080-e1de-11ee-a1d8-3f479df4d981(本博…...
Eureka和Nacos的关系
目录 它们的比较： 结论： Eureka和Nacos都是服务发现和注册中心，它们在微服务架构中扮演着关键角色，但它们是由不同的组织开发的，服务于类似但不完全相同的目的。以下是它们之间的关系： Eureka：…...
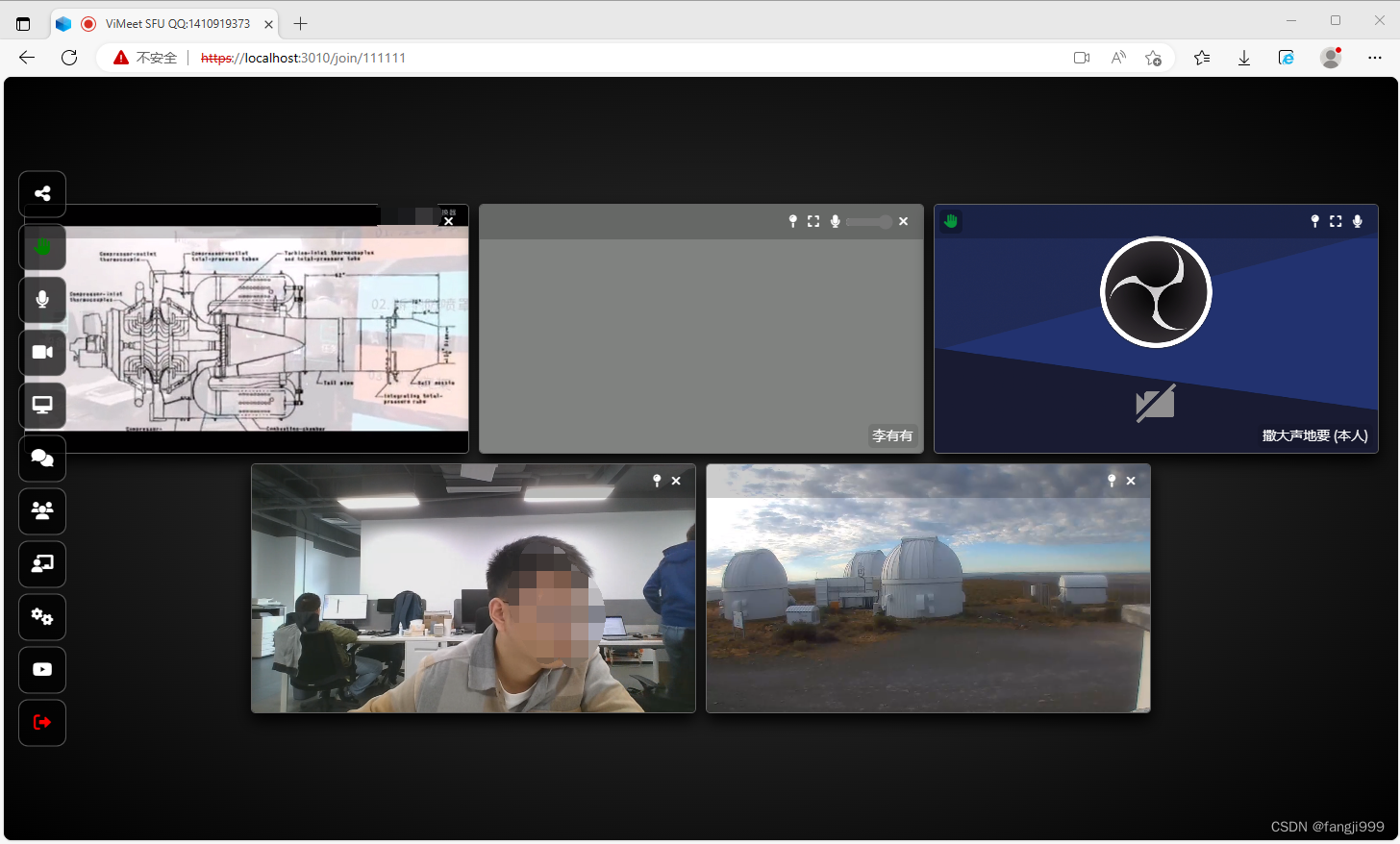
极简自建web视频会议，私有云，rtmp/rtsp/webrtc一键参会直播会议互动方案
随着视频互动深入工作日常，很多客户需要自建一个会议，监控的交互平台，目前外面不管是开源还是非开源的平台，都是极为复杂，一般linux安装库关联部署复杂，非技术人员根本没办法使用，不方便集成部署…...
5G智能网关助力工业铸造设备监测升级
随着物联网技术的迅猛发展和工业4.0浪潮的推进，传统工业正面临着严峻的转型升级压力。在这一背景下，铸造行业——这一典型的传统重工业领域，也必须积极探索借助5G、物联网、边缘计算等技术提升生产经营效率的新路径。 本文就基于佰马合作伙伴…...
奇舞周刊第523期：来自 rust 生态的强烈冲击？谈谈 Leptos 在语法设计上的精妙之处...
奇舞推荐 ■ ■ ■ 来自 rust 生态的强烈冲击？谈谈 Leptos 在语法设计上的精妙之处 过去很长一段时间，前端框架们都在往响应式的方向发展。同时又由于 React hooks 的深远影响，函数式 响应式成为了不少前端心中最理想的前端框架模样。Solid …...
《边缘计算：连接未来的智慧之桥》
随着物联网、5G等技术的快速发展，边缘计算作为一种新兴的计算模式，正逐渐引起人们的广泛关注。边缘计算通过将数据处理和存储功能放置在距离数据产生源头更近的位置，实现了更快速、更可靠的数据处理和交换，为各行各业带来了前所未…...
php 各种魔术函数的触发条件
2024.3.20 1、__construct() __construct() 用于在创建对象时自动触发 当使用 new 关键字实例化一个类时，会自动调用该类的 __construct() 方法 <?php class MyClass {public function __construct() {echo "已触发 __construct 一次";} }$obj new …...
Linux的学习之路：2、基础指令（1）
一、ls指令 上篇文章已经说了一点点的ls指令，不过那还是不够的，这篇文章会介绍更多的指令，最起码能使用命令行进行一些简单的操作，下面开始介绍了 ls常用选项 -a 列出目录下的所有文件，包括以 . 开头的隐含文件。 -d…...
0103设计算法-算法基础-算法导论第三版
文章目录 一、分治法二、分析分治算法结语 我们可以选择使用的算法设计技术有很多。插入排序使用了增量方法：在排序子数组 A [ 1 ⋯ j − 1 ] A[1\cdots j-1] A[1⋯j−1]后，将单个元素 A [ j ] A[j] A[j]插入子数组的适当位置，产生排序好的子…...
[NCTF2019]SQLi ---不会编程的崽
欸嘿，继续sql注入。又是新的sql注入类型 很直接哦，给出了sql查询语句。简单扫描一下，robots.txt还能访问。里边提示hint.txt $black_list "/limit|by|substr|mid|,|admin|benchmark|like|or|char|union|substring|select|greatest|%00…...
上位机开发 halcon坐标转轴坐标
背景 上位机开发中有一种相机叫标定相机，主要是有来给某些要进行根据CAD图点位计算时当前产品实际点位坐标时使用的一种标定测量相机。主要原理是根据两个或多个指定的标定点进行取图计算圆心坐标，再将视觉计算出的圆心坐标和取图时的轴坐标进行偏差计算。最后得到标定点轴的…...
[数据结构]二叉树(下)
一、二叉树的节点和深度关系 1.满二叉树 我们可以假设二叉树有N个节点，深度为h我们可以恒容易得到满二叉树每行的节点数，然后错位相减,算出节点与高度的关系。 2.完全二叉树 注意我这个是因为最后一行的节点数为1。 二、向上调整建堆和向下调整建堆的时…...
SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
华为云AI开发平台ModelArts
华为云ModelArts：重塑AI开发流程的“智能引擎”与“创新加速器”！ 在人工智能浪潮席卷全球的2025年，企业拥抱AI的意愿空前高涨，但技术门槛高、流程复杂、资源投入巨大的现实，却让许多创新构想止步于实验室。数据科学家…...
rknn优化教程（二）
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK，开始写第二篇的内容了。这篇博客主要能写一下： 如何给一些三方库按照xmake方式进行封装，供调用如何按…...
SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题（可多选） 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘：专注于发现数据中…...
江苏艾立泰跨国资源接力：废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下，江苏艾立泰以一场跨国资源接力的创新实践，重新定义了绿色供应链的边界。 跨国回收网络：废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点，将海外废弃包装箱通过标准…...
Frozen-Flask ：将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是：将一个 Flask Web 应用生成成纯静态 HTML 文件，从而可以部署到静态网站托管服务上，如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式：dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一，腐蚀跟膨胀属于反向操作，膨胀是把图像图像变大，而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
Git 3天2K星标：Datawhale 的 Happy-LLM 项目介绍（附教程）
引言 在人工智能飞速发展的今天，大语言模型（Large Language Models, LLMs）已成为技术领域的焦点。从智能写作到代码生成，LLM 的应用场景不断扩展，深刻改变了我们的工作和生活方式。然而，理解这些模型的内部…...