矩阵快速幂
快速幂

#include<iostream>
using namespace std;int main(){int a, b, p;cin>>a>>b>>p;int res = 1 % p;while(b){if(b & 1) res = 1ll * res * a % p;a = 1ll * a * a % p;b >>= 1;}cout<<res;return 0;
}
斐波那契数列

#include <iostream>
using namespace std;
typedef long long ll;
const int Nmax=10, mod=1e9;struct Matrix
{int n,m;int map[Nmax][Nmax];Matrix(int x,int y){n=x;m=y;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)map[i][j]=0;}Matrix operator * (const Matrix b){Matrix c(n,b.m);if(m==b.n){for(int i=1;i<=c.n;i++)for(int k=1;k<=m;k++)for(int j=1;j<=c.m;j++)c.map[i][j]=(c.map[i][j]+(map[i][k]*b.map[k][j])%mod)%mod;return c;}printf("error!!!!!!!!!!!!!!\n"); return c;}Matrix operator + (const Matrix b){Matrix c(n,m);if(m==b.m && n==b.n){for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)c.map[i][j]=(map[i][j]+b.map[i][j])%mod;return c;}printf("error!!!!!!!!!!!!!!\n"); return c;}void show(){printf("n:%d m:%d\n",n,m);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)printf("%4d%c",map[i][j],j==m?'\n':' ');}
};
int a,b,n;
int work()
{Matrix base(2,2);base.map[1][1]=a,base.map[1][2]=b;base.map[2][1]=1;//base.show();Matrix ans(2,2);ans.map[1][1]=1,ans.map[2][2]=1;if(n<=2)return 0*printf("1\n");n-=2;while(n){if(n&1)ans=ans*base;base=base*base;n>>=1;}Matrix now(2,1);now.map[1][1]=now.map[2][1]=1;//ans.show();ans=ans*now;//now.show();printf("%d\n",ans.map[1][1]);return 0;
}
int main()
{while(~scanf("%d%d%d",&a,&b,&n)){if(!a && !b && !n)break;work(); }return 0;
}
a ^ n + b ^ n

#include <iostream>
using namespace std;
typedef unsigned long long ll;
const int Nmax=10;
ll a,b,n;struct Matrix
{int n,m;ll map[Nmax][Nmax];Matrix(int x,int y){n=x;m=y;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)map[i][j]=0LLu;}Matrix operator * (const Matrix b){Matrix c(n,b.m);if(m==b.n){for(int i=1;i<=c.n;i++)for(int k=1;k<=m;k++)for(int j=1;j<=c.m;j++)c.map[i][j]=c.map[i][j]+map[i][k]*b.map[k][j];return c;}printf("error!!!!!!!!!!!!!!\n"); return c;}Matrix operator + (const Matrix b){Matrix c(n,m);if(m==b.m && n==b.n){for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)c.map[i][j]=map[i][j]+b.map[i][j];return c;}printf("error!!!!!!!!!!!!!!\n"); return c;}void show(){printf("n:%d m:%d\n",n,m);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)printf("%4llu%c",map[i][j],j==m?'\n':' ');}
};ll work()
{Matrix base(2,2);base.map[1][1]=a,base.map[1][2]=-b;base.map[2][1]=1LLu;//base.show();Matrix ans(2,2);ans.map[1][1]=1LLu,ans.map[2][2]=1LLu;ll newa=a*a-2LLu*b;if(n==2)return newa;if(n==1)return a;if(n==0)return 2LLu;n-=2LLu;while(n){if(n&1LLu)ans=ans*base;base=base*base;n>>=1;}Matrix now(2,1);now.map[1][1]=newa;now.map[2][1]=a;//ans.show();ans=ans*now;//now.show();return ans.map[1][1];
}
int main()
{while(~scanf("%llu%llu%llu",&a,&b,&n)){if(!a && !b && !n)break;printf("%llu\n",work());}return 0;
}
相关文章:

矩阵快速幂
快速幂 #include<iostream> using namespace std;int main(){int a, b, p;cin>>a>>b>>p;int res 1 % p;while(b){if(b & 1) res 1ll * res * a % p;a 1ll * a * a % p;b >> 1;}cout<<res;return 0; }斐波那契数列 #include <ios…...

数据之谜:解读Facebook的用户行为
在当今数字化时代,社交媒体平台已经成为人们生活中不可或缺的一部分,而Facebook作为全球最大的社交网络之一,其背后隐藏着许多数据之谜。本文将深入探讨Facebook的用户行为,并试图解读其中的奥秘。 用户行为数据的收集 Facebook作…...
学习 考证 帆软 FCP-FineBI V6.0 考试经验
学习背景: 自2024年1月起,大部分时间就在家里度过了,想着还是需要充实一下自己,我是一个充满热情的个体。由于之前公司也和帆软结缘,无论是 Fine-Report 和 Fine-BI 都有接触3年之久,但是主要做为管理者并…...
》)
《过滤器模式(极简c++)》
本文章属于专栏- 概述 - 《设计模式(极简c版)》-CSDN博客 本章简要说明过滤器模式。本文分为模式说明、本质思想、实践建议、代码示例四个部分。 模式说明 方案: 过滤器模式是一种结构型设计模式,用于过滤一组对象,基…...

【C++】如何用一个哈希表同时封装出unordered_set与unordered_map
👀樊梓慕:个人主页 🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C》《Linux》《算法》 🌝每一个不曾起舞的日子,都是对生命的辜负 目录 前言 1.哈希桶源码 2.哈希…...
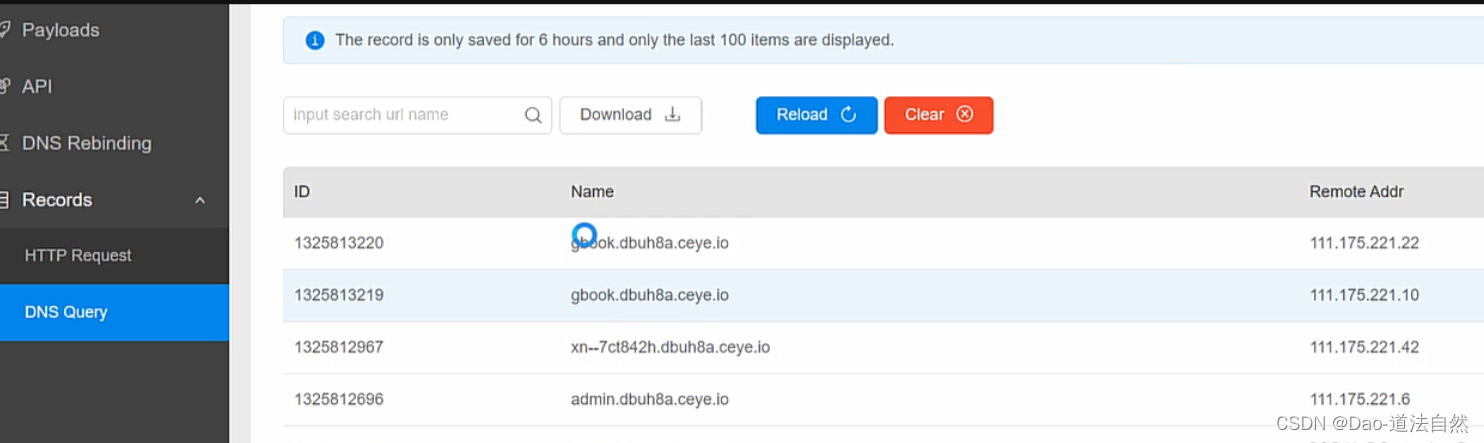
Day45:WEB攻防-PHP应用SQL二次注入堆叠执行DNS带外功能点黑白盒条件
目录 PHP-MYSQL-二次注入-DEMO&74CMS DEMO-用户注册登录修改密码 CMS-74CMS个人中心简历功能 PHP-MYSQL-堆叠注入-DEMO&CTF强网 Demo 2019强网杯-随便注(CTF题型) PHP-MYSQL-带外注入-DEMO&DNSLOG(让服务器主动把数据交出去) 知识点&…...

web安全之:三种常见的Web安全威胁
Web安全是确保Web应用和用户数据安全的一系列措施和实践。了解和防御常见的安全威胁是每个Web开发人员的基本职责。下面,我们将详细讨论三种常见的Web安全威胁:SQL注入、跨站脚本(XSS)和跨站请求伪造(CSRF)…...
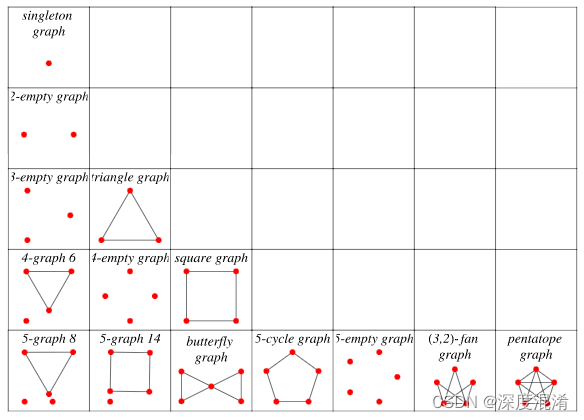
C#,图论与图算法,用于检查给定图是否为欧拉图(Eulerian Graph)的算法与源程序
1 欧拉图 欧拉图是指通过图(无向图或有向图)中所有边且每边仅通过一次通路, 相应的回路称为欧拉回路。具有欧拉回路的图称为欧拉图(Euler Graph), 具有欧拉通路而无欧拉回路的图称为半欧拉图。 对欧拉图的一个现代扩展是蜘蛛图,它向欧拉图增加了可以连接的存在点。 这给…...
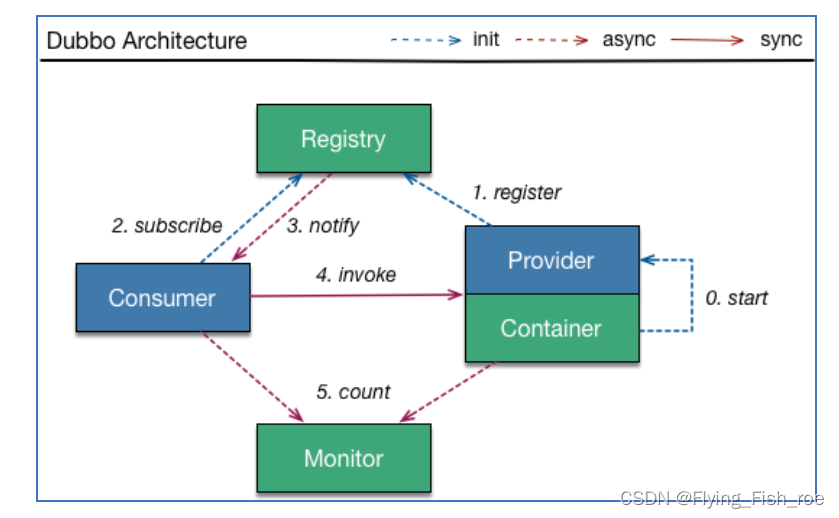
Dubbo框架的介绍
什么是dubbo Dubbo是一个高性能的、轻量级的开源RPC(远程过程调用)框架,由阿里巴巴公司开发并开源。它提供了基于Java的远程服务调用和管理的解决方案,可以帮助开发者快速构建分布式应用和服务。 Dubbo具有以下特点: …...

手机实时监控电脑屏幕(手机可以看到电脑在干什么吗)
已经2024年了,假如你还在问我,手机可以看到电脑在干什么吗,有没有手机实时监控电脑屏幕的系统。 那么证明,你可能已经out 了。 现代科技告诉发展的态势下,这种技术已经很成熟了。 域智盾软件就可以实现这种效果↓我们…...
合成孔径雷达干涉测量InSAR数据处理、地形三维重建、形变信息提取、监测
原文链接:合成孔径雷达干涉测量InSAR数据处理、地形三维重建、形变信息提取、监测https://mp.weixin.qq.com/s?__bizMzUzNTczMDMxMg&mid2247598798&idx7&snc054ed7c9d9c433d00837a7798080935&chksmfa820329cdf58a3f6b5986d6d4da3d19f81e3efd0b159f…...
云原生(五)、Docker-Swarm集群
基础环境说明 1、环境准备 1、启动4台服务器(在同一个网段内)。 2、重命名4台服务器,方便区分。 hostnamectl set-hostname swarm1 reboot安装docker。参考文章:云原生(二)、Docker基础 2、DockerSwarm…...

arm核的DMPIS是如何计算的
直接看这篇:https://zhuanlan.zhihu.com/p/660155292 写的很好: "SA8155P的CPU算力计算如下(按照A75性能提升50%来计算,即 5.2 * 1.5 7.8 DMIPS/MHz ) SA8155P算力 2.419GHz * 1核 * 7.8 DMIPS/MHz 2.131GH…...

Axure RP 9 for Mac中文激活版:原型设计工具
Axure RP 9 for Mac是一款值得设计师信赖的原型设计工具。它以其卓越的性能和稳定的运行赢得了广大用户的赞誉。 软件下载:Axure RP 9 for Mac中文激活版下载 在Axure RP 9中,您可以尽情发挥自己的设计才华,创造出独一无二的原型作品。无论是…...
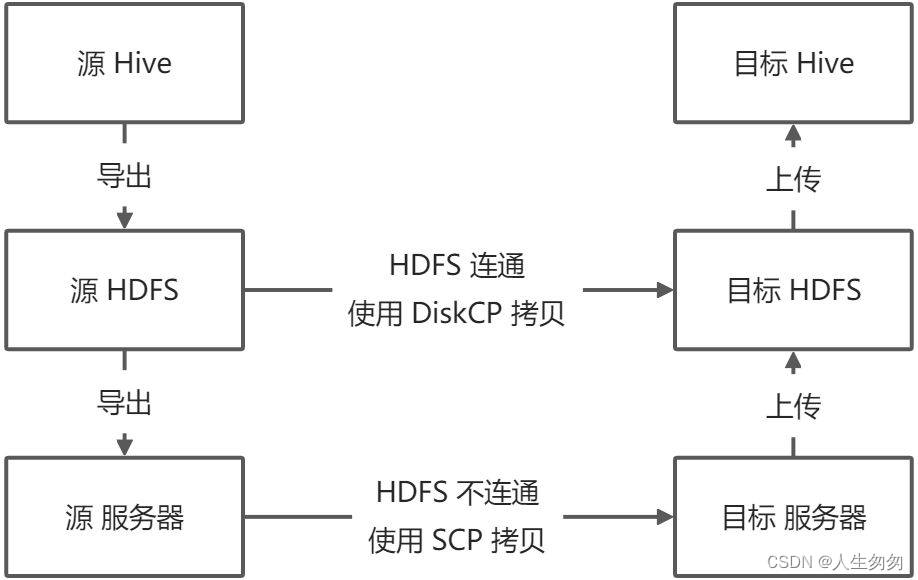
Hive 数据迁移与备份
迁移类型 同时迁移表及其数据(使用import和export) 迁移步骤 将表和数据从 Hive 导出到 HDFS将表和数据从 HDFS 导出到本地服务器将表和数据从本地服务器复制到目标服务器将表和数据从目标服务器上传到目标 HDFS将表和数据从目标 HDFS 上传到目标 Hiv…...

FFMpeg 获取音频音量、提高音量
查看音量 准备原生音频original.mp3 查看original.mp3的音量信息: ffmpeg -i original.mp3 -filter_complex volumedetect -c:v copy -f null /dev/null输出: Input #0, mp3, from original.mp3:Metadata:artist : Administratorencoder …...

【java数据结构】基于java提供的ArrayList实现的扑克牌游戏-(附源码~)
【Java数据结构】基于java泛型实现的二维数组完成三人扑克游戏 基本框架的实现创建一副牌如何进行洗牌:每个人抓的牌放到哪里: 源码具体实现cardcardsTest 个人简介:努力学编程 每日鸡汤:stay foolish,stay hungry-史蒂芬.乔布斯斯…...
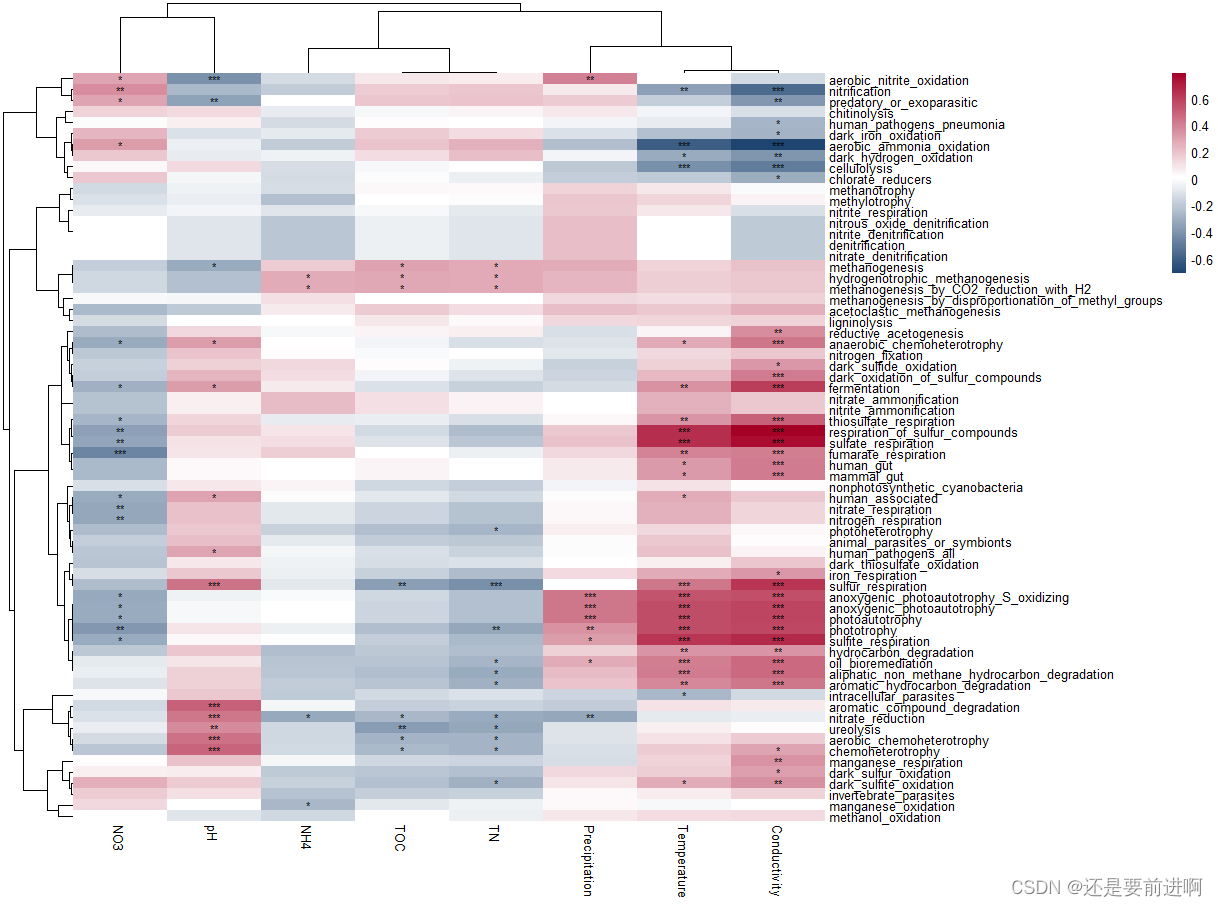
R语言:microeco:一个用于微生物群落生态学数据挖掘的R包,第八:trans_func class
# 生态学研究人员通常对微生物群落的功能特征感兴趣,因为功能或代谢数据对于解释微生物群落的结构和动态以及推断其潜在机制是强有力的。 # 由于宏基因组测序复杂且昂贵,利用扩增子测序数据预测功能谱是一个很好的选择。 # 有几个软件经常用于此目标&…...

王道c语言-二叉树前序、中序、后序、层次遍历
main.cpp #include "function.h"//abdhiejcfg 前序遍历深度优先遍历 abdhiejcfg void PreOrder(BiTree p) {if (p ! NULL) {printf("%c ", p->c);//等价于putchar(p->c);等价于visit函数伪代码PreOrder(p->lchild);PreOrder(p->rchild);} }//…...
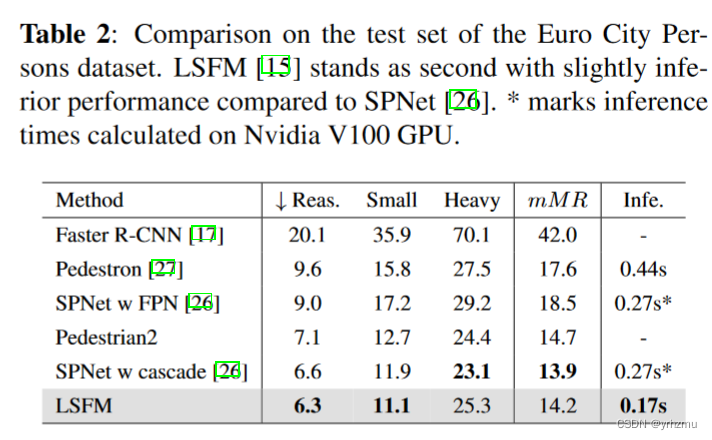
<REAL-TIME TRAFFIC OBJECT DETCTION FOR AUTONOMOUS DRIVING>论文阅读
Abstract 随着计算机视觉的最新进展,自动驾驶迟早成为现代社会的一部分,然而,仍有大量的问题需要解决。尽管现代计算机视觉技术展现了优越的性能,他们倾向于将精度优先于效率,这是实时应用的一个重要方面。大型目标检测…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
