R语言:microeco:一个用于微生物群落生态学数据挖掘的R包,第八:trans_func class
# 生态学研究人员通常对微生物群落的功能特征感兴趣,因为功能或代谢数据对于解释微生物群落的结构和动态以及推断其潜在机制是强有力的。
# 由于宏基因组测序复杂且昂贵,利用扩增子测序数据预测功能谱是一个很好的选择。
# 有几个软件经常用于此目标,如PICRUSt, Tax4Fun和FAPROTAX。
# 这些工具可以很好地用于基于测序结果的原核生物群落的功能谱预测。此外,获得每个分类群或OTU的功能也很重要,
# 而不仅仅是整个群落的概况。但是很难知道每个OTU的确切功能。FAPROTAX数据库是根据已发表在书籍和文献中的已知研究成果,
# 对原核生物的性状和特征进行的汇总。我们将原核生物的分类信息与该数据库进行比对,以确定原核生物在生物地球化学作用上的特征。
# 我们还实现了FUNGuild和FungalTraits数据库来识别真菌性状。
> t1 <- trans_func$new(dataset = dataset)
> t1$cal_spe_func(prok_database = "FAPROTAX")
> t1$cal_spe_func(fungi_database = "FungalTraits")
# 计算群落中具有特定性状的物种百分比。具有特定性状的分类群所占百分比可以反映群落中相应的功能潜力。
# 因此,该方法是一种不考虑类群间系统发育距离的功能冗余表示。
> t1$cal_spe_func_perc(abundance_weighted = TRUE)
> t1$show_prok_func(use_func = "methanotrophy")
> t1$plot_spe_func_perc()
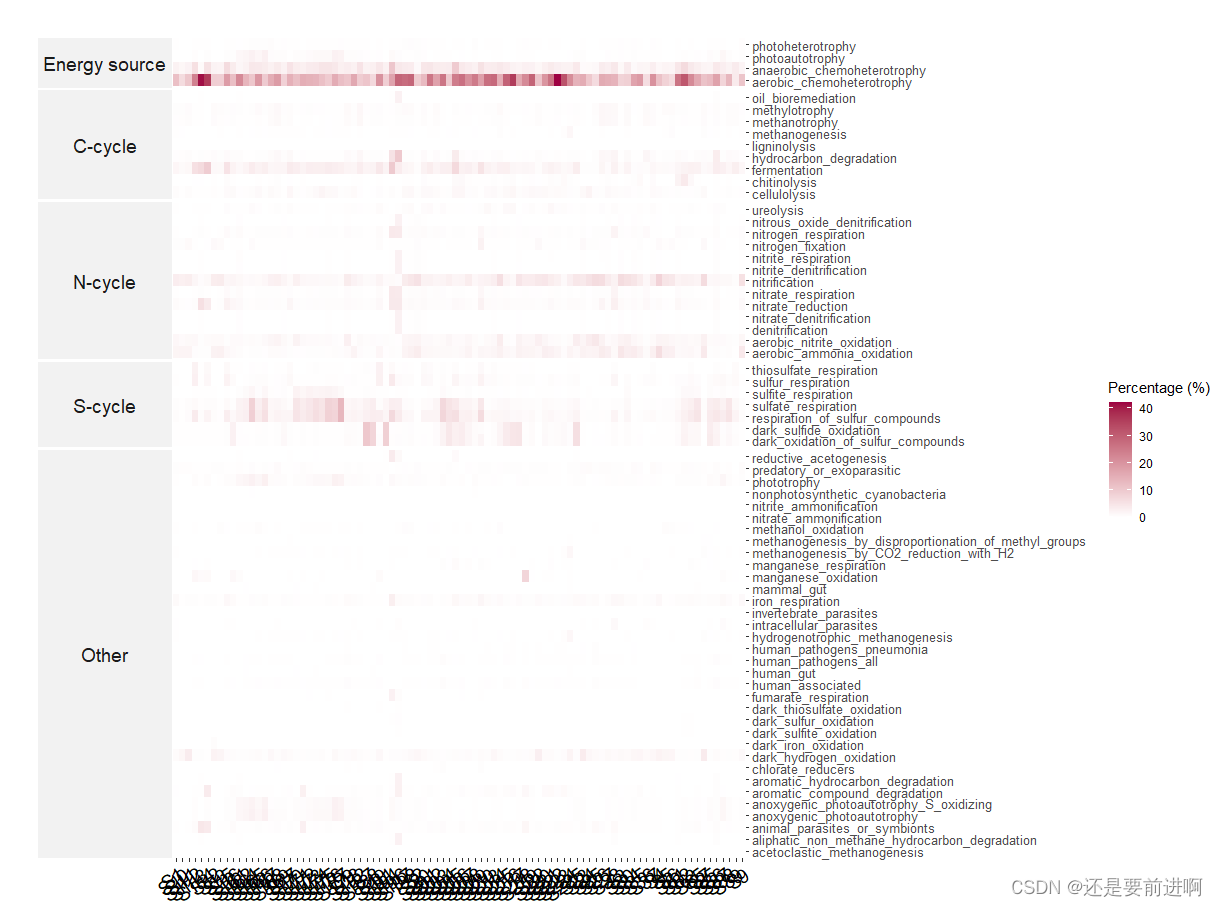
#然后我们尝试将社区的res_spe_func_perc与环境变量联系起来
> t3 <- trans_env$new(dataset = dataset, add_data = env_data_16S[, 4:11])
> t3$cal_cor(add_abund_table = t1$res_spe_func_perc, cor_method = "spearman")
> library(pheatmap)
> t3$plot_cor(pheatmap = TRUE)
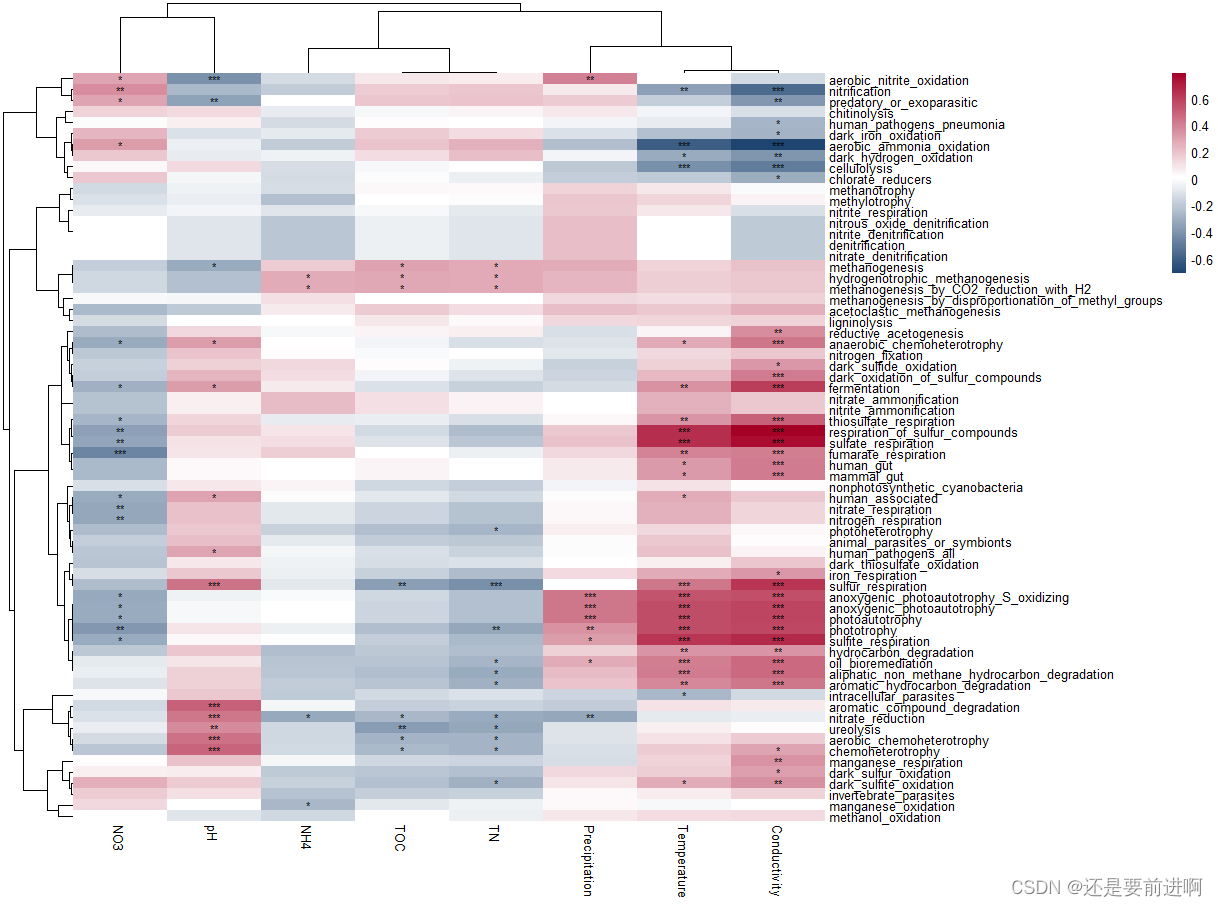
microeco就先分享到这里,这个包比较复杂,我只是分享了部分,想要学习,得从事具体的项目。这些代码,我都跑过一边,大家可以先跑跑。
相关文章:

R语言:microeco:一个用于微生物群落生态学数据挖掘的R包,第八:trans_func class
# 生态学研究人员通常对微生物群落的功能特征感兴趣,因为功能或代谢数据对于解释微生物群落的结构和动态以及推断其潜在机制是强有力的。 # 由于宏基因组测序复杂且昂贵,利用扩增子测序数据预测功能谱是一个很好的选择。 # 有几个软件经常用于此目标&…...

王道c语言-二叉树前序、中序、后序、层次遍历
main.cpp #include "function.h"//abdhiejcfg 前序遍历深度优先遍历 abdhiejcfg void PreOrder(BiTree p) {if (p ! NULL) {printf("%c ", p->c);//等价于putchar(p->c);等价于visit函数伪代码PreOrder(p->lchild);PreOrder(p->rchild);} }//…...
<REAL-TIME TRAFFIC OBJECT DETCTION FOR AUTONOMOUS DRIVING>论文阅读
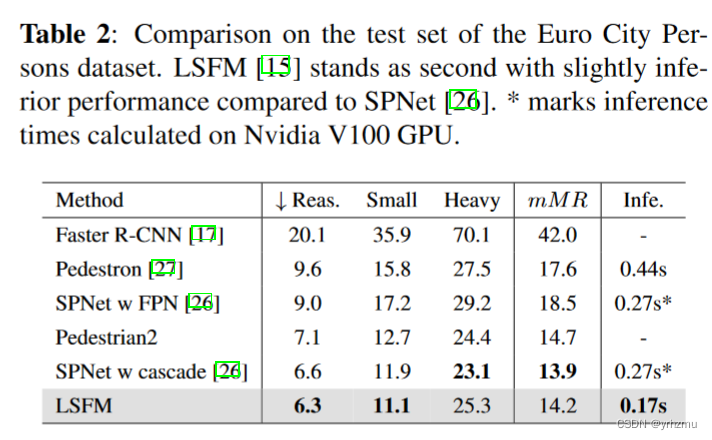
Abstract 随着计算机视觉的最新进展,自动驾驶迟早成为现代社会的一部分,然而,仍有大量的问题需要解决。尽管现代计算机视觉技术展现了优越的性能,他们倾向于将精度优先于效率,这是实时应用的一个重要方面。大型目标检测…...

优化 - 排序算法
一、概念 冒泡排序从左往右比较相邻的两个元素,右比左小就换位,这样最大值就出现在了右边最后一个元素上,再从左边第一个元素开始往右比较到倒数第二个元素,如此重复...选择排序 通过线性查找(从左往右挨个查找&#…...

Python实战:深拷贝与浅拷贝
1. 引言 在Python中,对象是通过对内存中的数据进行引用来实现的。当我们创建一个对象并将其赋值给另一个变量时,实际上是将这个对象的引用复制给了另一个变量。这意味着,如果原始对象发生改变,引用该对象的变量也会受到影响。为了…...

rollup打包起手式
使用Rollup打包JavaScript rollup是一款小巧的javascript模块打包工具,更适合于库应用的构建工具;可以将小块代码编译成大块复杂的代码,基于ES6 modules,它可以让你的 bundle 最小化,有效减少文件请求大小,vue在开发的时候用的是webpack,但是…...

【笔记】语言实例比较 3. 无重复字符的最长子串 C++ Rust Java Python
语言实例比较 3. 无重复字符的最长子串 C Rust Java Python C C: 9ms O ( N 2 ) O(N^2) O(N2), 8.68MB mem O ( 1 ) O(1) O(1) 滑动窗口循环 class Solution { public:int lengthOfLongestSubstring(const string s) {//s[start,end) 前面包含 后面不包含int res(0);for (…...

int的大小你知道时4个字节,那么类的大小你知道怎么计算吗?
文章目录 1、如何计算类对象的大小2、类对象的存储方式猜测3、结构体内存对齐规则1、如何计算类对象的大小 class A { public: void PrintA() { cout<<_a<<endl; } private: char _a; };问题: 类中既可以有成员变量,又可以有成员函数,那么一个类的对象中包含了…...
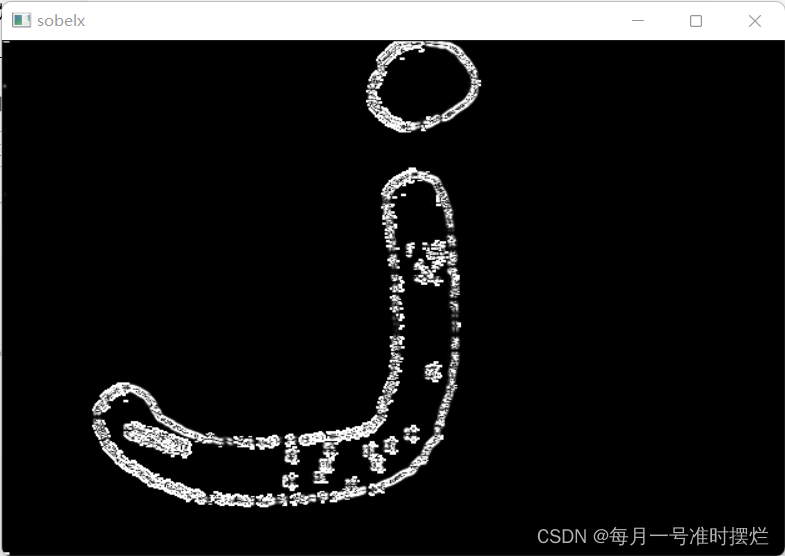
OpenCV学习笔记(十一)——利用Sobel算子计算梯度
Sobel算子是基于一阶导数的离散差分算子,其中Sobel对于像素值的变化是十分敏感的,在进行边缘检测的时候,Sobel算子常用于对周围像素的重要性进行检测。 Sobel算子包括检验水平方向的算子和检测竖直方向的算子 计算机梯度值的操作如下&#x…...

扩展一下BenchmarkSQL,新增支持ASE/HANA/DB2/SQLServer,可以随便用了
1 背景 提到数据库的性能,自然就避不开性能测试。有专用于测试OLTP的,也有偏重于OLAP的。本文介绍的BenchmarkSQL就属于测试OLTP中的一个,基于TPCC的。网上有很多介绍TPC*的相关测试的文章,大家可以自行脑补。而PostgreSQL自带的pgbench是属于TPCC的前一个基准测试程序,偏…...

Android 静默安装成功后自启动
近期开发上线一个常驻app,项目已上线,今天随笔记录一下静默安装相关内容。我分三篇静默安装(root版)、静默安装(无障碍版)、监听系统更新、卸载、安装。 先说说我的项目需求:要求app一直运行&am…...

计算机二级真题讲解每日一题:《format格式化》
描述 在右侧答题模板中修改代码,删除代码中的横线,填写代码,完成如下功能。 接收用户输入的一个小于 20的正整数,在屏幕上逐行递增显示从 01 到该正整数,数字显示的宽度为 2,不足位置补 0,后面追…...
RabbitMQ问题
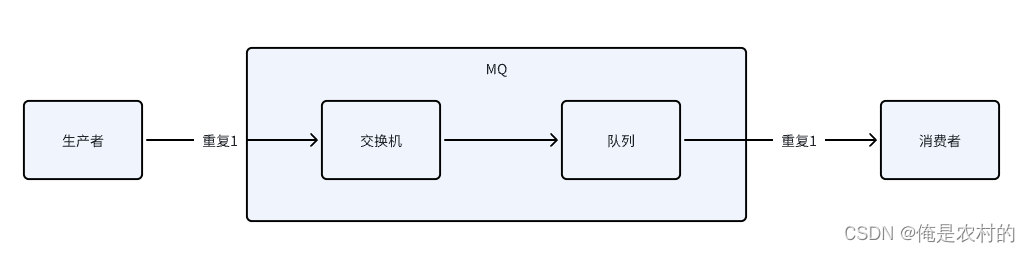
如何实现顺序消费? 消息放入到同一个队列中消费 如何解决消息不丢失? 方案: 如上图:消息丢失有三种情况,解决了以上三种情况就解决了丢失的问题 1、丢失1--->消息在到达交换机的时候;解决࿱…...

flutter->Scaffold左侧/右侧侧边栏和UserAccountsDrawerHeader的使用
//appBar的 leading/actions 和 Scaffold的drawer/endDrawer 冲突只能存在一个 import package:flutter/material.dart;void main() {runApp(MyApp()); }class MyApp extends StatelessWidget {const MyApp({super.key});overrideWidget build(BuildContext context) {retur…...
vulnhub prime1通关
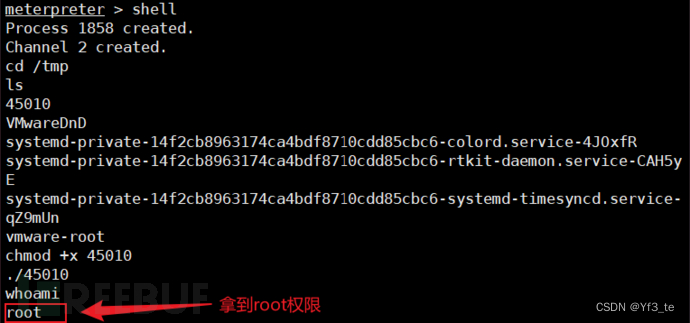
目录 环境安装 1.信息收集 收集IP 端口扫描 目录扫描 目录文件扫描 查找参数 打Boss 远程文件读取 木马文件写入 权限提升 方法一 解锁密钥 方法二: linux内核漏洞提权 总结 环境安装 Kali2021.4及其prime靶机 靶机安装:Prime: 1 ~ Vul…...
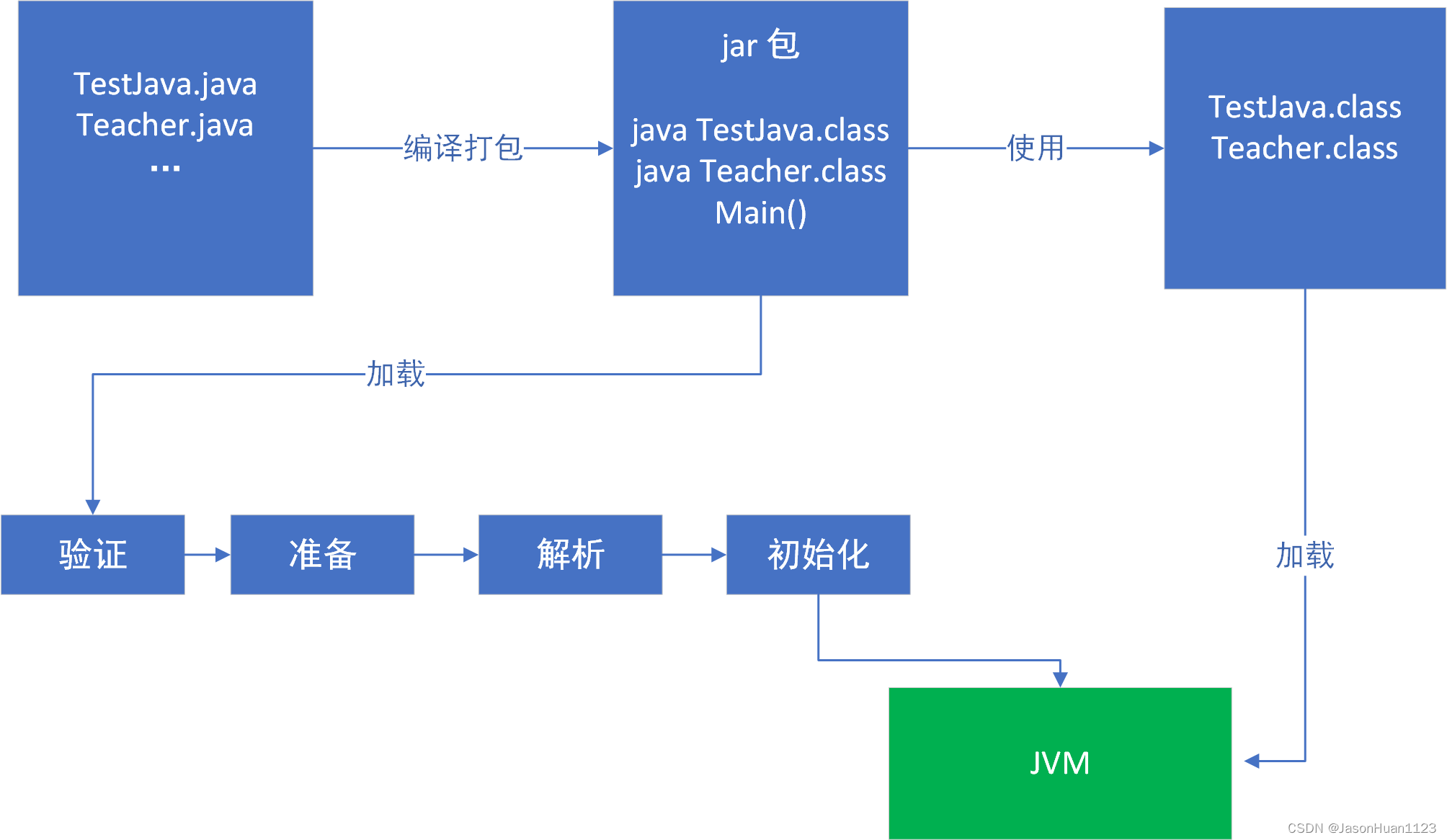
JVM快速入门(1)JVM体系结构、运行时数据区、类加载器、线程共享和独享、分区、Java对象实例化
5.1 JVM体系结构 线程独占区-程序计数器(Program Counter Register) 程序计数器是一块较小的内存空间,它可以看做是当前线程所执行的字节码的行号指示器;在虚拟机的概念模型里,字节码解释器工作时就是通过改变这个计数…...

CSS3新属性(学习笔记)
一、. 圆角 border-radius:; 可以取1-4个值(规则同margin) 可以取px和% 一般用像素,画圆的时候用百分比:border-radius:50%; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8&q…...

41-Vue-webpack基础
webpack基础 前言什么是webpackwebpack的基本使用指定webpack的entry和output 前言 本篇开始来学习下webpack的使用 什么是webpack webpack: 是前端项目工程化的具体解决方案。 主要功能:它提供了友好的前端模块化开发支持,以及代码压缩混淆、处理浏览…...

数据仓库的分层理论
数据仓库的分层理论是为了更好地组织和管理数据,支持复杂的数据分析和决策支持。在这一理论中,数据仓库被分为多个层次,每个层次都有其特定的作用和设计原则。以下是每一层的详细介绍,以及以销售人员为例的Doris建表实例。 ODS层…...
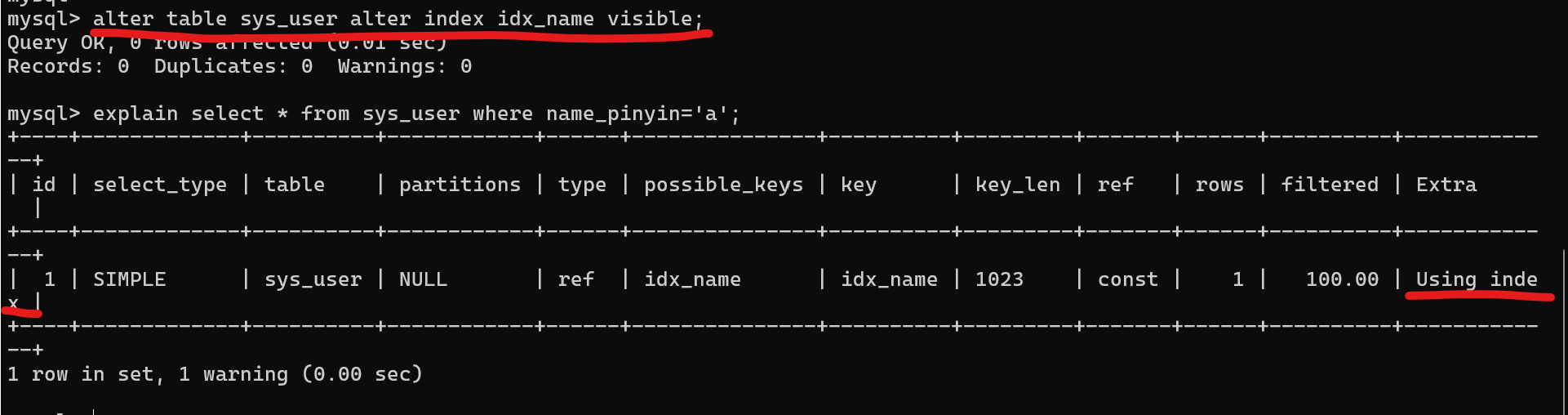
MySQL 8.0-索引- 不可见索引(invisible indexes)
概述 MySQL 8.0引入了不可见索引(invisible index),这个在实际工作用还是用的到的,我觉得可以了解下。 在介绍不可见索引之前,我先来看下invisible index是个什么或者定义。 我们依然使用拆开来看,然后再把拆出来的词放到MySQL…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
