Python实战:深拷贝与浅拷贝
1. 引言
在Python中,对象是通过对内存中的数据进行引用来实现的。当我们创建一个对象并将其赋值给另一个变量时,实际上是将这个对象的引用复制给了另一个变量。这意味着,如果原始对象发生改变,引用该对象的变量也会受到影响。为了解决这个问题,Python提供了深拷贝和浅拷贝两种方式来复制对象。
2. 浅拷贝的原理与实现
浅拷贝(Shallow Copy)是指复制一个对象时,只复制对象本身及其包含的元素,但不复制元素所引用的对象。在Python中,可以使用copy模块的copy()函数来实现浅拷贝。
示例1:浅拷贝列表
import copy
list1 = [1, 2, [3, 4]]
list2 = copy.copy(list1)
list1[0] = 0
list1[2][0] = 0
print(list1) # 输出:[0, 2, [0, 4]]
print(list2) # 输出:[1, 2, [0, 4]]
在这个示例中,我们对list1进行了浅拷贝,生成了list2。当修改list1的第一个元素时,list2的第一个元素不受影响。但是,当我们修改list1的第三个元素(一个列表)时,list2的对应元素也发生了改变。这是因为浅拷贝只复制了列表本身,但没有复制列表中的元素所引用的对象。
3. 深拷贝的原理与实现
深拷贝(Deep Copy)是指复制一个对象时,不仅复制对象本身,还复制对象所引用的所有对象。在Python中,可以使用copy模块的deepcopy()函数来实现深拷贝。
示例2:深拷贝列表
import copy
list1 = [1, 2, [3, 4]]
list2 = copy.deepcopy(list1)
list1[0] = 0
list1[2][0] = 0
print(list1) # 输出:[0, 2, [0, 4]]
print(list2) # 输出:[1, 2, [3, 4]]
在这个示例中,我们对list1进行了深拷贝,生成了list2。当修改list1的第一个元素时,list2的第一个元素不受影响。同样,当我们修改list1的第三个元素(一个列表)时,list2的对应元素也没有发生改变。这是因为深拷贝复制了列表本身以及列表中的元素所引用的对象。
4. 深拷贝与浅拷贝的应用场景
在实际编程中,深拷贝和浅拷贝的应用场景取决于我们对数据的需求。以下是一些常见的应用场景:
(1)当需要复制一个对象,并且不希望原始对象与复制对象之间存在关联时,可以使用深拷贝。
(2)当需要复制一个对象,并且希望原始对象与复制对象共享一部分数据时,可以使用浅拷贝。
(3)在处理大型数据结构时,深拷贝可能会消耗较多的内存和计算资源。在这种情况下,可以考虑使用浅拷贝。
5. 总结
本文详细介绍了Python中的深拷贝与浅拷贝的原理、实现方法以及在实际编程中的应用。通过具体代码示例,我们了解到深拷贝和浅拷贝的区别以及如何选择合适的复制方式。掌握这两种复制方式对于高效地处理Python中的数据结构至关重要。
相关文章:

Python实战:深拷贝与浅拷贝
1. 引言 在Python中,对象是通过对内存中的数据进行引用来实现的。当我们创建一个对象并将其赋值给另一个变量时,实际上是将这个对象的引用复制给了另一个变量。这意味着,如果原始对象发生改变,引用该对象的变量也会受到影响。为了…...

rollup打包起手式
使用Rollup打包JavaScript rollup是一款小巧的javascript模块打包工具,更适合于库应用的构建工具;可以将小块代码编译成大块复杂的代码,基于ES6 modules,它可以让你的 bundle 最小化,有效减少文件请求大小,vue在开发的时候用的是webpack,但是…...

【笔记】语言实例比较 3. 无重复字符的最长子串 C++ Rust Java Python
语言实例比较 3. 无重复字符的最长子串 C Rust Java Python C C: 9ms O ( N 2 ) O(N^2) O(N2), 8.68MB mem O ( 1 ) O(1) O(1) 滑动窗口循环 class Solution { public:int lengthOfLongestSubstring(const string s) {//s[start,end) 前面包含 后面不包含int res(0);for (…...

int的大小你知道时4个字节,那么类的大小你知道怎么计算吗?
文章目录 1、如何计算类对象的大小2、类对象的存储方式猜测3、结构体内存对齐规则1、如何计算类对象的大小 class A { public: void PrintA() { cout<<_a<<endl; } private: char _a; };问题: 类中既可以有成员变量,又可以有成员函数,那么一个类的对象中包含了…...
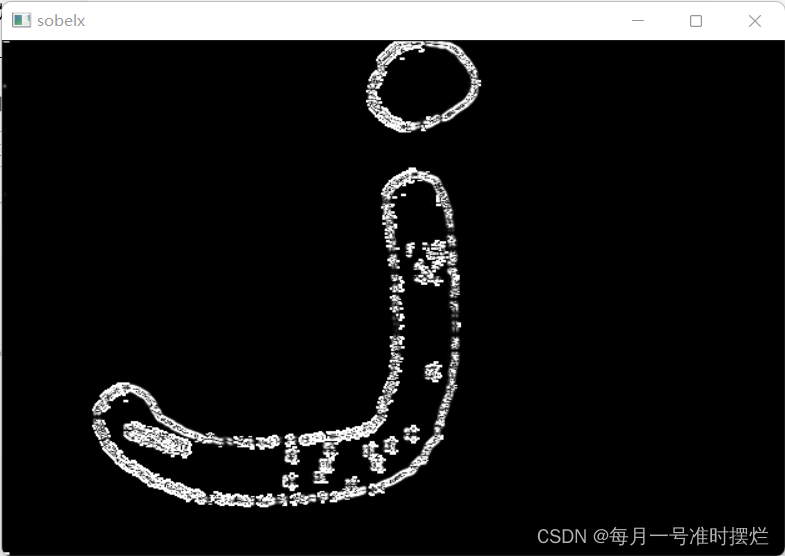
OpenCV学习笔记(十一)——利用Sobel算子计算梯度
Sobel算子是基于一阶导数的离散差分算子,其中Sobel对于像素值的变化是十分敏感的,在进行边缘检测的时候,Sobel算子常用于对周围像素的重要性进行检测。 Sobel算子包括检验水平方向的算子和检测竖直方向的算子 计算机梯度值的操作如下&#x…...

扩展一下BenchmarkSQL,新增支持ASE/HANA/DB2/SQLServer,可以随便用了
1 背景 提到数据库的性能,自然就避不开性能测试。有专用于测试OLTP的,也有偏重于OLAP的。本文介绍的BenchmarkSQL就属于测试OLTP中的一个,基于TPCC的。网上有很多介绍TPC*的相关测试的文章,大家可以自行脑补。而PostgreSQL自带的pgbench是属于TPCC的前一个基准测试程序,偏…...

Android 静默安装成功后自启动
近期开发上线一个常驻app,项目已上线,今天随笔记录一下静默安装相关内容。我分三篇静默安装(root版)、静默安装(无障碍版)、监听系统更新、卸载、安装。 先说说我的项目需求:要求app一直运行&am…...

计算机二级真题讲解每日一题:《format格式化》
描述 在右侧答题模板中修改代码,删除代码中的横线,填写代码,完成如下功能。 接收用户输入的一个小于 20的正整数,在屏幕上逐行递增显示从 01 到该正整数,数字显示的宽度为 2,不足位置补 0,后面追…...
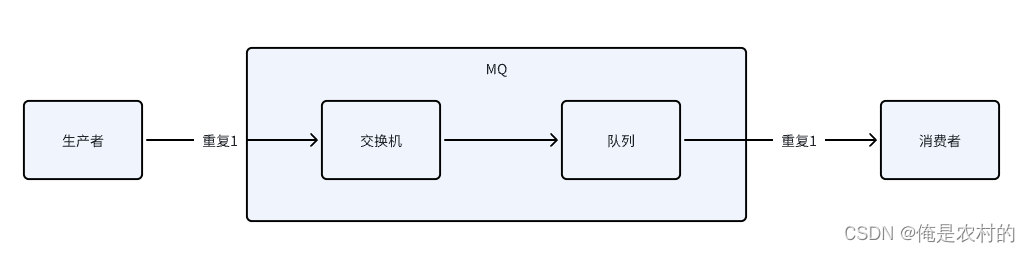
RabbitMQ问题
如何实现顺序消费? 消息放入到同一个队列中消费 如何解决消息不丢失? 方案: 如上图:消息丢失有三种情况,解决了以上三种情况就解决了丢失的问题 1、丢失1--->消息在到达交换机的时候;解决࿱…...

flutter->Scaffold左侧/右侧侧边栏和UserAccountsDrawerHeader的使用
//appBar的 leading/actions 和 Scaffold的drawer/endDrawer 冲突只能存在一个 import package:flutter/material.dart;void main() {runApp(MyApp()); }class MyApp extends StatelessWidget {const MyApp({super.key});overrideWidget build(BuildContext context) {retur…...
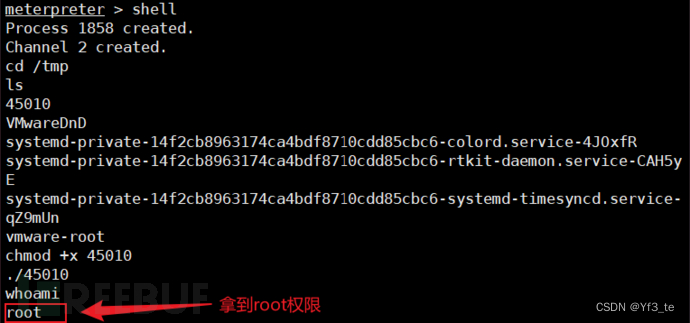
vulnhub prime1通关
目录 环境安装 1.信息收集 收集IP 端口扫描 目录扫描 目录文件扫描 查找参数 打Boss 远程文件读取 木马文件写入 权限提升 方法一 解锁密钥 方法二: linux内核漏洞提权 总结 环境安装 Kali2021.4及其prime靶机 靶机安装:Prime: 1 ~ Vul…...
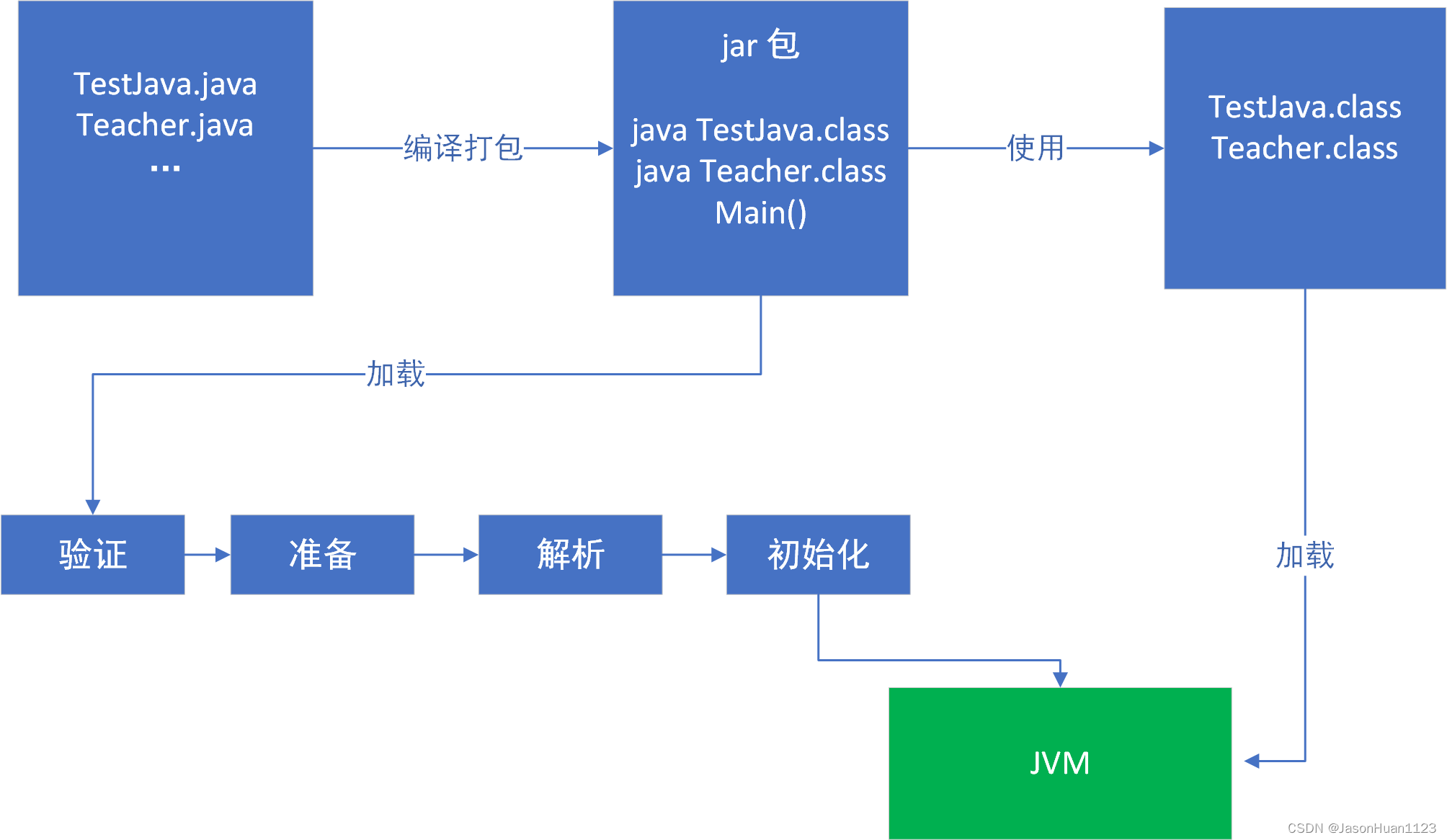
JVM快速入门(1)JVM体系结构、运行时数据区、类加载器、线程共享和独享、分区、Java对象实例化
5.1 JVM体系结构 线程独占区-程序计数器(Program Counter Register) 程序计数器是一块较小的内存空间,它可以看做是当前线程所执行的字节码的行号指示器;在虚拟机的概念模型里,字节码解释器工作时就是通过改变这个计数…...

CSS3新属性(学习笔记)
一、. 圆角 border-radius:; 可以取1-4个值(规则同margin) 可以取px和% 一般用像素,画圆的时候用百分比:border-radius:50%; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8&q…...

41-Vue-webpack基础
webpack基础 前言什么是webpackwebpack的基本使用指定webpack的entry和output 前言 本篇开始来学习下webpack的使用 什么是webpack webpack: 是前端项目工程化的具体解决方案。 主要功能:它提供了友好的前端模块化开发支持,以及代码压缩混淆、处理浏览…...

数据仓库的分层理论
数据仓库的分层理论是为了更好地组织和管理数据,支持复杂的数据分析和决策支持。在这一理论中,数据仓库被分为多个层次,每个层次都有其特定的作用和设计原则。以下是每一层的详细介绍,以及以销售人员为例的Doris建表实例。 ODS层…...
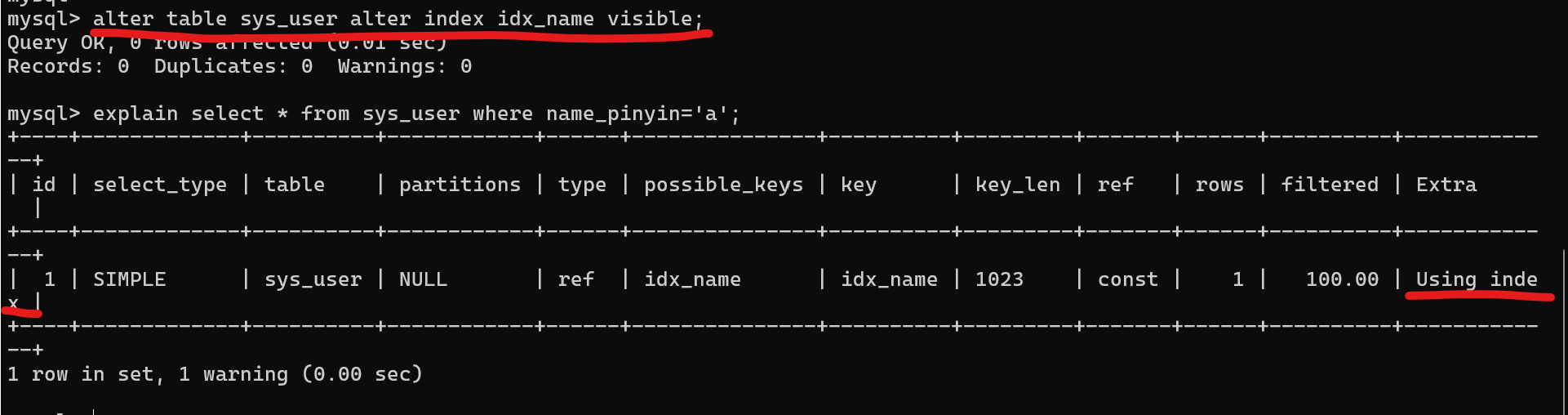
MySQL 8.0-索引- 不可见索引(invisible indexes)
概述 MySQL 8.0引入了不可见索引(invisible index),这个在实际工作用还是用的到的,我觉得可以了解下。 在介绍不可见索引之前,我先来看下invisible index是个什么或者定义。 我们依然使用拆开来看,然后再把拆出来的词放到MySQL…...

Uibot6.0 (RPA财务机器人师资培训第3天 )财务招聘信息抓取机器人案例实战
训练网站:泓江科技 (lessonplan.cn)https://laiye.lessonplan.cn/list/ec0f5080-e1de-11ee-a1d8-3f479df4d981https://laiye.lessonplan.cn/list/ec0f5080-e1de-11ee-a1d8-3f479df4d981https://laiye.lessonplan.cn/list/ec0f5080-e1de-11ee-a1d8-3f479df4d981(本博…...

Eureka和Nacos的关系
目录 它们的比较: 结论: Eureka和Nacos都是服务发现和注册中心,它们在微服务架构中扮演着关键角色,但它们是由不同的组织开发的,服务于类似但不完全相同的目的。以下是它们之间的关系: Eureka:…...
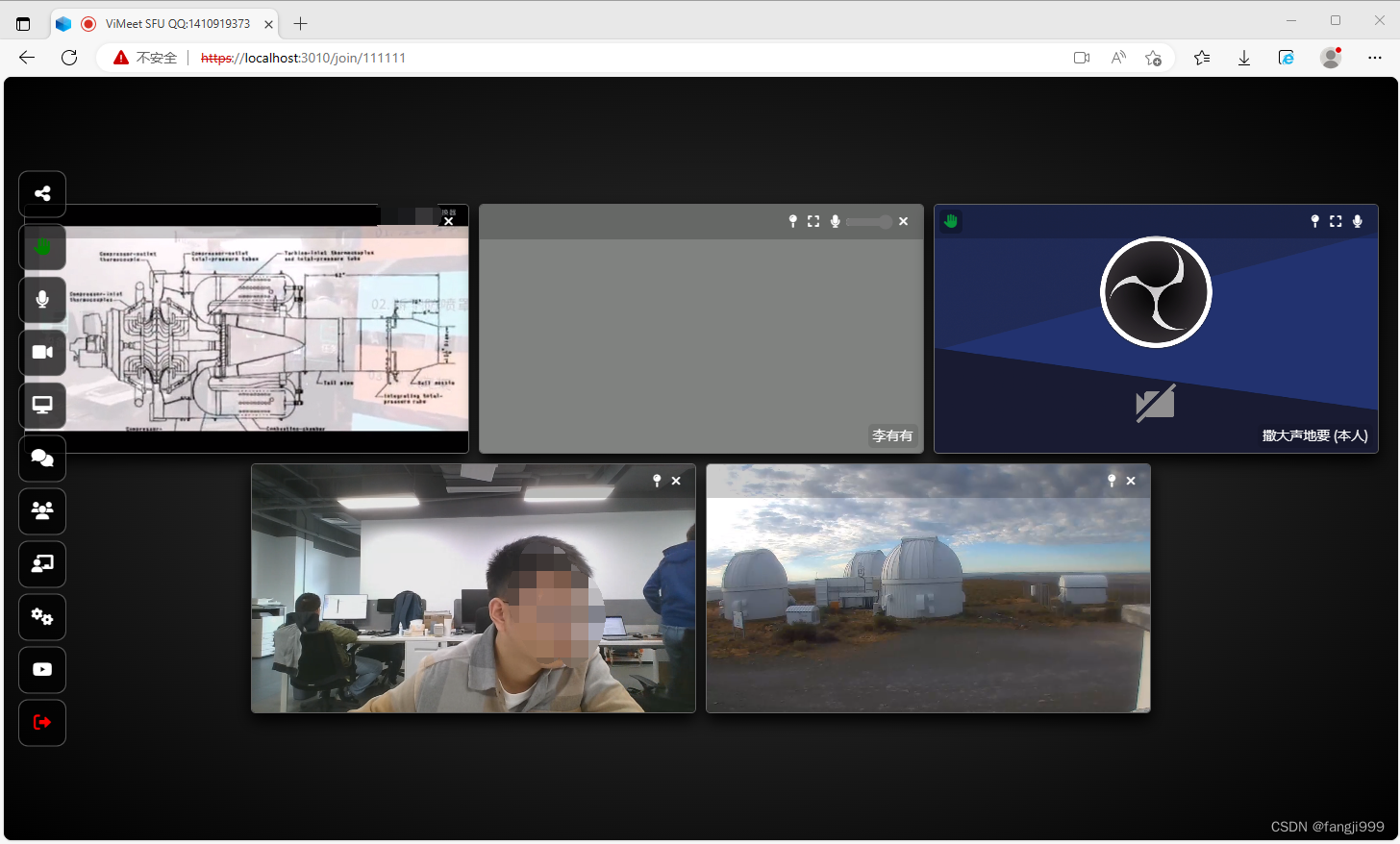
极简自建web视频会议,私有云,rtmp/rtsp/webrtc一键参会直播会议互动方案
随着视频互动深入工作日常,很多客户需要自建一个会议,监控的交互平台,目前外面不管是开源还是非开源的平台,都是极为复杂,一般linux安装库关联部署复杂,非技术人员根本没办法使用,不方便集成部署…...
5G智能网关助力工业铸造设备监测升级
随着物联网技术的迅猛发展和工业4.0浪潮的推进,传统工业正面临着严峻的转型升级压力。在这一背景下,铸造行业——这一典型的传统重工业领域,也必须积极探索借助5G、物联网、边缘计算等技术提升生产经营效率的新路径。 本文就基于佰马合作伙伴…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...
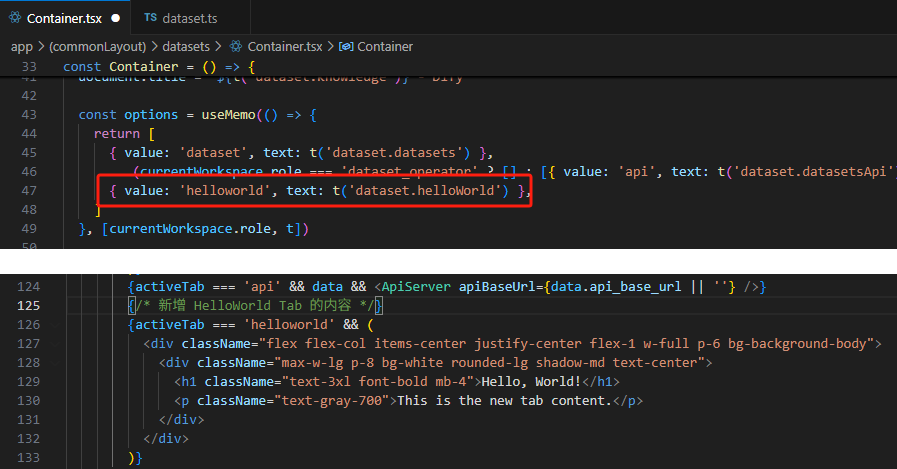
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...
