深度学习-2.9梯度不稳定和Glorot条件
梯度不稳定和Glorot条件
一、梯度消失和梯度爆炸
对于神经网络这个复杂系统来说,在模型训练过程中,一个最基础、同时也最常见的问题,就是梯度消失和梯度爆炸。
我们知道,神经网络在进行反向传播的过程中,各参数层的梯度计算会涉及到激活函数导函数取值,具体来说,假设现在有一个三层的神经网络,其中两个隐藏层的激活函数为 F ( x ) F(x) F(x),对应的导函数为 f ( x ) f(x) f(x),设X为输入训练的数据特征,y为标签, y ^ \hat{y} y^为模型向前传播输出结果,$ w_1 为第一层参数、 为第一层参数、 为第一层参数、w_2 为第二层参数、 为第二层参数、 为第二层参数、w_3$为第三层参数,loss为损失函数,则有如下计算公式:
每一次正向传播计算结果:
y ^ = F ( F ( X ∗ w 1 ) ∗ w 2 ) ∗ w 3 \hat y = F(F(X * w_1) * w_2) * w_3 y^=F(F(X∗w1)∗w2)∗w3
而loss是一个关于y和 y ^ \hat{y} y^的函数,而y是常量, y ^ \hat{y} y^是一个关于w的函数,因此 l o s s loss loss也进行如下表示:
l o s s ( y ^ ) loss(\hat{y}) loss(y^)
在进行梯度求解时候,假设 w 1 w_1 w1对应梯度为 g r a d 1 grad_1 grad1, w 2 w_2 w2对应梯度为 g r a d 2 grad_2 grad2, w 3 w_3 w3对应梯度为 g r a d 3 grad_3 grad3,为了简化计算,我们假设所有的 x 、 w 1 、 w 2 、 w 3 x、w_1、w_2、w_3 x、w1、w2、w3都是标量,根据链式法则,有计算过程如下:
g r a d 1 = ∂ l o s s ∂ w 1 = ∂ l o s s ∂ y ^ ⋅ ∂ y ^ ∂ w 1 = ∂ l o s s ∂ y ^ ⋅ ∂ ( F ( F ( X ∗ w 1 ) ∗ w 2 ) ∗ w 3 ) ∂ w 1 = ∂ l o s s ∂ y ^ ⋅ ∂ ( F ( F ( X ∗ w 1 ) ∗ w 2 ) ∗ w 3 ) ∂ ( F ( F ( X ∗ w 1 ) ∗ w 2 ) ⋅ ∂ F ( F ( X ∗ w 1 ) ∗ w 2 ) ∂ F ( X ∗ w 1 ) ⋅ ∂ F ( X ∗ w 1 ) ∂ w 1 = ∂ l o s s ∂ y ^ ⋅ w 3 ⋅ f ( F ( X ∗ w 1 ) ∗ w 2 ) ⋅ w 2 ⋅ f ( X ∗ w 1 ) ⋅ X \begin{aligned} grad_1 &=\frac{\partial loss}{\partial w_1} \\ &= \frac{\partial loss}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w_1} \\ &= \frac{\partial loss}{\partial \hat y} \cdot \frac{\partial (F(F(X * w_1) * w_2) * w_3)}{\partial w_1} \\ &= \frac{\partial loss}{\partial \hat y} \cdot \frac{\partial (F(F(X * w_1) * w_2) * w_3)}{\partial (F(F(X * w_1) * w_2)} \cdot \frac{\partial F(F(X * w_1) * w_2)}{\partial F(X * w_1)} \cdot \frac{\partial F(X * w_1)}{\partial w_1}\\ &= \frac{\partial loss}{\partial \hat y} \cdot w_3 \cdot f(F(X * w_1) * w_2) \cdot w_2 \cdot f(X * w_1) \cdot X \\ \end{aligned} grad1=∂w1∂loss=∂y^∂loss⋅∂w1∂y^=∂y^∂loss⋅∂w1∂(F(F(X∗w1)∗w2)∗w3)=∂y^∂loss⋅∂(F(F(X∗w1)∗w2)∂(F(F(X∗w1)∗w2)∗w3)⋅∂F(X∗w1)∂F(F(X∗w1)∗w2)⋅∂w1∂F(X∗w1)=∂y^∂loss⋅w3⋅f(F(X∗w1)∗w2)⋅w2⋅f(X∗w1)⋅X
值得注意的是,此时 g r a d 1 grad_1 grad1中计算了两次激活函数的导函数,并且在上述过程中, X ∗ w 1 X * w_1 X∗w1是第一层隐藏层接收到的数据,而 F ( X ∗ w 1 ) ∗ w 2 F(X*w_1)*w_2 F(X∗w1)∗w2则是第二层隐藏层接收到的数据。而对比如果是计算 w 2 w_2 w2的梯度,则有如下过程:
g r a d 2 = ∂ l o s s ∂ w 2 = ∂ l o s s ∂ y ^ ⋅ ∂ y ^ ∂ w 2 = ∂ l o s s ∂ y ^ ⋅ ∂ ( F ( F ( X ∗ w 1 ) ∗ w 2 ) ∗ w 3 ) ∂ w 2 = ∂ l o s s ∂ y ^ ⋅ ∂ ( F ( F ( X ∗ w 1 ) ∗ w 2 ) ∗ w 3 ) ∂ ( F ( F ( X ∗ w 1 ) ∗ w 2 ) ⋅ ∂ F ( F ( X ∗ w 1 ) ∗ w 2 ) ∂ w 2 = ∂ l o s s ∂ y ^ ⋅ w 3 ⋅ ∂ F ( F ( X ∗ w 1 ) ∗ w 2 ) ∂ w 2 = ∂ l o s s ∂ y ^ ⋅ w 3 ⋅ f ( F ( X ∗ w 1 ) ∗ w 2 ) ⋅ ∂ ( F ( X ∗ w 1 ) ∗ w 2 ) ∂ w 2 = ∂ l o s s ∂ y ^ ⋅ w 3 ⋅ f ( F ( X ∗ w 1 ) ∗ w 2 ) ⋅ F ( X ∗ w 1 ) \begin{aligned} grad_2 &=\frac{\partial loss}{\partial w_2} \\ &= \frac{\partial loss}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w_2} \\ &= \frac{\partial loss}{\partial \hat y} \cdot \frac{\partial (F(F(X * w_1) * w_2) * w_3)}{\partial w_2} \\ &= \frac{\partial loss}{\partial \hat y} \cdot \frac{\partial (F(F(X * w_1) * w_2) * w_3)}{\partial (F(F(X * w_1) * w_2)} \cdot \frac{\partial F(F(X * w_1) * w_2)}{\partial w_2} \\ &= \frac{\partial loss}{\partial \hat y} \cdot w_3 \cdot \frac{\partial F(F(X * w_1) * w_2)}{\partial w_2} \\ &= \frac{\partial loss}{\partial \hat y} \cdot w_3 \cdot f(F(X*w_1)*w_2) \cdot \frac{\partial (F(X * w_1) * w_2)}{\partial w_2} \\ &= \frac{\partial loss}{\partial \hat y} \cdot w_3 \cdot f(F(X*w_1)*w_2) \cdot F(X * w_1) \\ \end{aligned} grad2=∂w2∂loss=∂y^∂loss⋅∂w2∂y^=∂y^∂loss⋅∂w2∂(F(F(X∗w1)∗w2)∗w3)=∂y^∂loss⋅∂(F(F(X∗w1)∗w2)∂(F(F(X∗w1)∗w2)∗w3)⋅∂w2∂F(F(X∗w1)∗w2)=∂y^∂loss⋅w3⋅∂w2∂F(F(X∗w1)∗w2)=∂y^∂loss⋅w3⋅f(F(X∗w1)∗w2)⋅∂w2∂(F(X∗w1)∗w2)=∂y^∂loss⋅w3⋅f(F(X∗w1)∗w2)⋅F(X∗w1)
我们发现,在计算过程中只出现了一次激活函数的导函数。当然如果我们是计算 w 3 w_3 w3的梯度,则与如下计算过程:
g r a d 3 = ∂ l o s s ∂ w 3 = ∂ l o s s ∂ y ^ ⋅ ∂ y ^ ∂ w 3 = ∂ l o s s ∂ y ^ ⋅ ∂ ( F ( F ( X ∗ w 1 ) ∗ w 2 ) ∗ w 3 ) ∂ w 3 = ∂ l o s s ∂ y ^ ⋅ F ( F ( X ∗ w 1 ) ∗ w 2 ) \begin{aligned} grad_3 &=\frac{\partial loss}{\partial w_3} \\ &= \frac{\partial loss}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w_3} \\ &= \frac{\partial loss}{\partial \hat y} \cdot \frac{\partial (F(F(X * w_1) * w_2) * w_3)}{\partial w_3} \\ &= \frac{\partial loss}{\partial \hat y} \cdot F(F(X * w_1) * w_2) \\ \end{aligned} grad3=∂w3∂loss=∂y^∂loss⋅∂w3∂y^=∂y^∂loss⋅∂w3∂(F(F(X∗w1)∗w2)∗w3)=∂y^∂loss⋅F(F(X∗w1)∗w2)
此时 g r a d 3 grad_3 grad3在计算过程中就已经不涉及激活函数的导函数的计算了。
其实如果当神经网络层数继续增加、激活函数的数量继续增加,第一层参数在计算梯度的过程中需要相乘的激活函数导函数个数也会随之增加,而后面几层参数的梯度计算中涉及到的激活函数导函数个数逐级递减。
当然,上述过程如果换成矩阵求导,公式主体部分基本不变,只有最后一项会发生变化。由于最终运算结果无法写成较为简洁的矩阵运算形式(矩阵变元的实向量函数),因此此处以标量运算为例。
而累乘就容易造成指数级变化,当激活函数值 F ( F ( X ∗ w 1 ) ) F(F(X*w_1)) F(F(X∗w1))、激活函数导函数值 f ( X ∗ w 1 ) f(X*w_1) f(X∗w1)或者参与相乘的参数取值( w 3 w_3 w3)较大(>1)时,会出现 g r a d 1 grad_1 grad1远大于 g r a d 2 grad_2 grad2远大于 g r a d 3 grad_3 grad3的情况,也就是神经网络前几层参数梯度非常大、而后几层参数梯度相对较小的情况,此时就被称为梯度爆炸,并且受到累乘效应的影响,前几层梯度也会大于甚至远大于1,此时就会造成模型迭代过程不稳定的情况发生;而反之如果上述几个变量均小于1,甚至远小于1,则会出现前几层参数梯度非常小、而后几层参数梯度非常大的情况,此时就被称为梯度消失,此时由于模型各层参数学习率伴随层数增加逐渐增加,并且由于构成梯度的基本参数均小于1,因此最后几层梯度也会小于1甚至远小于1,此时前几层参数梯度取值将非常小,甚至趋于0,因而会使得前几层的参数无法在迭代中得到更新。
总结一下,不同层参数的梯度在计算过程中都有很大的差异,并且这种差异是一种累乘效应,我们也可以简单理解为是一种伴随着层数增加指数级变化的差异。而这种累乘效应会导致线性层参数的一部分梯度过大而另一部分过小,从而影响模型平稳训练。而从具体原因来说,每一层参数的梯度主要和两个因素相关,其一是线性层输入数据,如 X X X或 F ( X ∗ W ) F(X*W) F(X∗W),其二则是激活函数导函数计算结果 f ( X ∗ w 1 ) f(X*w_1) f(X∗w1)。
接下来,我们就从梯度消失和梯度爆炸的角度剖析Sigmoid和tanh激活函数叠加过程中可能存在的隐患。
二、Sigmoid和tanh激活函数的梯度更新问题
1.Sigmoid激活函数的梯度消失问题
- 理论说明
对于sigmoid激活函数来说,简答的叠加是极容易出现梯度消失的问题。sigmoid函数及导函数图像如下所示:


我们发现,Sigmoid导函数最大值为0.25(在0点处取到),当x较大或者较小时,导函数取值趋于0。
此时如果我们假设还是上述结构的三层神经网络,则第一层参数梯度 g r a d 1 grad_1 grad1由于计算过程出现两次导函数连乘,哪怕两次都导函数都取到最大值(虽然可能性较小), g r a d 1 grad_1 grad1都将在0.0625的基础上进行其余部分相乘,最终结果也极有可能是个非常小的值,因此对于Sigmoid激活函数叠加的情况来说,是极容易出现梯度消失情况的。
g r a d 1 = ∂ l o s s ∂ y ^ ⋅ w 3 ⋅ f ( F ( X ∗ w 1 ) ∗ w 2 ) ⋅ w 2 ⋅ f ( X ∗ w 1 ) ⋅ X grad_1 = \frac{\partial loss}{\partial \hat y} \cdot w_3 \cdot f(F(X*w_1)*w_2) \cdot w_2 \cdot f(X * w_1) \cdot X grad1=∂y^∂loss⋅w3⋅f(F(X∗w1)∗w2)⋅w2⋅f(X∗w1)⋅X
g r a d 2 = ∂ l o s s ∂ y ^ ⋅ w 3 ⋅ f ( F ( X ∗ w 1 ) ∗ w 2 ) ⋅ F ( X ∗ w 1 ) grad_2 = \frac{\partial loss}{\partial \hat y} \cdot w_3 \cdot f(F(X*w_1)*w_2) \cdot F(X * w_1) grad2=∂y^∂loss⋅w3⋅f(F(X∗w1)∗w2)⋅F(X∗w1)
g r a d 3 = ∂ l o s s ∂ y ^ ⋅ F ( F ( X ∗ w 1 ) ∗ w 2 ) 梯度消失或者梯度爆炸,始终是个概率问题。我们不能说导函数取值取值小就一定会发生梯度消失问题,只是导函数最大值越小,越有可能发生梯度消失。 grad_3 = \frac{\partial loss}{\partial \hat y} \cdot F(F(X * w_1) * w_2)\> 梯度消失或者梯度爆炸,始终是个概率问题。我们不能说导函数取值取值小就一定会发生梯度消失问题,只是导函数最大值越小,越有可能发生梯度消失。 grad3=∂y^∂loss⋅F(F(X∗w1)∗w2)梯度消失或者梯度爆炸,始终是个概率问题。我们不能说导函数取值取值小就一定会发生梯度消失问题,只是导函数最大值越小,越有可能发生梯度消失。
- Sigmoid函数饱和区间
一般来说我们会将靠近sigmoid函数的左右两端的区间称为函数的饱和区间(如下图圈出部分)(也就是自变量绝对值较大的区间),不难发现,当自变量落入饱和区间时,因变量会趋于0或者1,而无论自变量是极小(负数绝对值极大)还是极大,都会使得导函数取值趋于0,从而更容易导致模型梯度消失。

设计一个函数,构建一个使用了三层sigmoid激活层的函数

将多层网络的权重进行输出:
for i, m in enumerate(sigmoid_model3.modules()):if isinstance(m, nn.Linear):vp_x = m.weight.grad.detach().reshape(-1, 1).numpy() # 每一层参数梯度vp_y = np.full_like(vp_x, i) # 对层进行标记vp_a = np.concatenate((vp_x, vp_y), 1)vp.append(vp_a)

类似的,tanh也存在问题:

随着训练次数的增多,网络之间的权重逐渐消失,模型无法有效学习,最终影响模型效果。
三、Zero-Centered Data与Glorot条件
通过对Sigmoid和tanh激活函数叠加后的模型梯度变化情况分析,我们不难发现,梯度不平稳是影响模型建模效果的非常核心的因素。而这个看似简单问题的解决方案,却花费了研究人员数十年的时间才逐渐完善,我们现在所接触到的优化方法,也基本上是在15年前后提出的,而这些被验证的切实可行的优化方法,也是推动这一轮深度学习浪潮的技术因素。
当然,这些优化方法主要是针对深层次神经网络的。
整体来看,针对梯度不平稳的解决方案(优化方法)总共分为五类,分别是参数初始化方法、输入数据的归一化方法、衍生激活函数使用方法、学习率调度方法以及梯度下降优化方法。接下来,先介绍所有上述优化算法的一个基本理论,由Xavier Glorot在2010提出的Glorot条件。
值得注意的是,虽然不同优化算法有不同的出发点和不同的论证方式,但基本都可以从Glorot条件出发进行思考。
1.Zero-centered Data
在介绍Glorot条件之前,我们先从一个更加朴素的角度出发,讨论关于Zero-Centered Data相关作用,从而帮助我们理解后续Glorot条件。
首先,我们还是假设当前模型是一个三层神经网络,其中两个隐藏层的激活函数为 F ( x ) F(x) F(x),对应的导函数为 f ( x ) f(x) f(x),设X为输入训练的数据特征,y为标签, y ^ \hat y y^为模型向前传播输出结果, w 1 w_1 w1为第一层参数、 w 2 w_2 w2为第二层参数、 w 3 w_3 w3为第三层参数,loss为损失函数,则有如下计算公式:
每一次正向传播计算结果:
y ^ = F ( F ( X ∗ w 1 ) ∗ w 2 ) ∗ w 3 \hat y = F(F(X * w_1) * w_2) * w_3 y^=F(F(X∗w1)∗w2)∗w3
假设 Z i Z_i Zi为第i层接收到的数据, P i P_i Pi为第i层输出的数据,则有:
Z 1 = X ∗ w 1 Z_1 = X*w_1 Z1=X∗w1
P 1 = F ( Z 1 ) = F ( X ∗ w 1 ) P_1 = F(Z_1) = F(X*w_1) P1=F(Z1)=F(X∗w1)
Z 2 = P 1 ∗ w 2 = F ( X ∗ w 1 ) ∗ w 2 Z_2 = P_1 * w_2 = F(X*w_1)*w_2 Z2=P1∗w2=F(X∗w1)∗w2
P 2 = F ( Z 2 ) = F ( F ( X ∗ w 1 ) ∗ w 2 ) P_2 = F(Z_2) = F(F(X*w_1)*w_2) P2=F(Z2)=F(F(X∗w1)∗w2)
Z 3 = y ^ = F ( F ( X ∗ w 1 ) ∗ w 2 ) ∗ w 3 Z_3 = \hat y = F(F(X * w_1) * w_2) * w_3 Z3=y^=F(F(X∗w1)∗w2)∗w3
依次类推。而在反向传播过程,各参数层的梯度如下:
g r a d 1 = ∂ l o s s ∂ y ^ ⋅ w 3 ⋅ f ( F ( X ∗ w 1 ) ∗ w 2 ) ⋅ w 2 ⋅ f ( X ∗ w 1 ) ⋅ X grad_1 = \frac{\partial loss}{\partial \hat y} \cdot w_3 \cdot f(F(X*w_1)*w_2) \cdot w_2 \cdot f(X * w_1) \cdot X grad1=∂y^∂loss⋅w3⋅f(F(X∗w1)∗w2)⋅w2⋅f(X∗w1)⋅X
g r a d 2 = ∂ l o s s ∂ y ^ ⋅ w 3 ⋅ f ( F ( X ∗ w 1 ) ∗ w 2 ) ⋅ F ( X ∗ w 1 ) grad_2 = \frac{\partial loss}{\partial \hat y} \cdot w_3 \cdot f(F(X*w_1)*w_2) \cdot F(X * w_1) grad2=∂y^∂loss⋅w3⋅f(F(X∗w1)∗w2)⋅F(X∗w1)
g r a d 3 = ∂ l o s s ∂ y ^ ⋅ F ( F ( X ∗ w 1 ) ∗ w 2 ) grad_3 = \frac{\partial loss}{\partial \hat y} \cdot F(F(X * w_1) * w_2) grad3=∂y^∂loss⋅F(F(X∗w1)∗w2)
在梯度消失和梯度爆炸的案例中,我们不难发现,为了确保多层神经网络的有效性,各层梯度的差距不应太大,此时一个最为基本的想法就是,就是能否让所有的输入数据(也就是X)以及所有层的参数都设置为Zero-Centered Data,也就是零点对称数据,不难发现,由于X和 w i w_i wi都是零点对称的,因此每一个线性层中的导函数也取值也能够维持在0-1之间,进而每一层的梯度基本能维持在比较平稳的状态。
另外,除了能够避免梯度不平稳问题以外,创建Zero-Centered的参数和数据集,还能够更好的在正向传播中将信息传播到各层,以及确保各层学习的平稳性。
关于如何将带入模型训练的数据转化为Zero-Centered Data,一般来说我们会使用一系列标准化方法对其进行转化,具体方法我们会在Lesson 14进行详细介绍,由于我们此前创建的数据生成器生成的就是Zero-Centered Data,因此暂时这些数据不会影响接下来的优化方法使用。而如何将参数转化为Zero-Centered Data,就是核心需要考虑的问题了。
对于输入的数据来说,我们可以尽量保证其Zero-Centered的特性,但模型参数是随着模型迭代不断变化的,我们无法把控模型每一轮迭代后的情况,因此只能从模型参数初始值入手,尽量保证其Zero-Centered属性。
很明显,我们不能将参数的初始值全部设为0,我们只能考虑借助统计工具生成均值是0的随机数,也就是0均值的均匀分布或者是0均值的高斯分布,但这里需要考虑的另一个问题就是,该随机数的方差应该如何确定?
2.Glorot条件和Xavier方法
初始化参数的方差如何确定这一问题在一个严谨论述如何保证模型有效性的论文中,从另一个角度出发,得到了回答。根据Xavier Glorot在2010年发表的《Understanding the difficulty of training deep feedforward neural networks》论文中的观点,为保证模型本身的有效性和稳定性,我们希望正向传播时,每个线性层输入数据的方差等于输出数据的方差,同时我们也希望反向传播时,数据流经某层之前和流经某层之后该层的梯度也具有相同的方差,虽然二者很难同时满足(除非相邻两层神经元个数相同),但Glorot和Bengio(论文第二作者)表示,如果我们适当修改计算过程、是可以找到一种折中方案去设计初始参数取值,从而同时保证二者条件尽可能得到满足,这种设计参数初始值的方法也被称为Xavier方法,而这种方法也经过一段时间的实践验证被证明是很好的一种初始化模型参数的方法,尤其是对于使用tanh激活函数的神经网络来说,效果更为显著。
而这种正向传播时数据方差保持一致、反向传播时参数梯度方差保持一致的条件,也被称为Glorot条件,满足该条件的模型能够进行有效平稳的训练,而为了满足该条件而创建的(当然也是由上述论文提出的)模型初始化参数值设计方法,也被称为Xavier方法。而在Xavier方法中,最核心解决的问题,也就是为了创建Zero-Centered的初始化参数时参数的方差。和我们从朴素的角度思考的方向是一致的。
由于Glorot条件和Xavier方法是在2010年提出的,彼时ReLU激活函数还未兴起,因此Xavier方法主要是围绕tanh激活函数可能存在的梯度爆炸或梯度消失进行的优化,Sigmoid激活函数效果次之。不过尽管如此,Glorot条件却是一个通用条件,后续围绕ReLU激活函数、用于解决神经元活性失效的优化方法(如HE初始化方法),也是遵照Glorot条件进行的方法设计。
3.模型初始化参数取值影响
Xavier初始化方法的推导和使用我们将在下一节详细介绍,此处我们先通过另外一个实例,去展示为何初始参数取值不同,会够得到不同的建模结果。模型初始化时得到的不同参数,本质上等价于在损失函数上找到了不同的初始点,而同一损失函数,初始点选取的不同应该不会影响最终迭代结果才对,但事实情况并非如此。

我们发现,初始参数值的选取不仅会影响模型收敛速度,甚至在某些情况下还会影响模型的最终表现。造成此现象的根本原因还是在于神经网络模型在进行训练时,不确定性过多,而在一个拥有诸多不确定性的系统中再加上不确定的初始参数,初始参数的不确定性会被这个系统放大。并且,值得一提的是,每一个epoch中的每一次迭代并不是在一个损失函数上一步步下降的,当我们使用小批量梯度下降算法时,带入不同批的数据,实际创建的损失函数也会不同。
参考
菜菜子的深度学习
相关文章:

深度学习-2.9梯度不稳定和Glorot条件
梯度不稳定和Glorot条件 一、梯度消失和梯度爆炸 对于神经网络这个复杂系统来说,在模型训练过程中,一个最基础、同时也最常见的问题,就是梯度消失和梯度爆炸。 我们知道,神经网络在进行反向传播的过程中,各参数层的梯…...

地宫取宝dfs
分析: 矩阵里的每一个位置都有标记,要求的问题是:有几种方法能完成这个规定。 那么,我们只需要计算从开始(1,1)到最后(n,m)的深度优先搜索中,有几个是满足要求的即为正确答案。 有个要求是,如果一个格子中…...

Ollama 运行 Cohere 的 command-r 模型
Ollama 运行 Cohere 的 command-r 模型 0. 引言1. 安装 MSYS22. 安装 Golang3. Build Ollama4. 运行 command-r 0. 引言 Command-R Command-R 是一种大型语言模型,针对对话交互和长上下文任务进行了优化。它针对的是“可扩展”类别的模型,这些模型在高…...

2024年C语言最新经典面试题汇总(11-20)
C语言文章更新目录 C语言学习资源汇总,史上最全面总结,没有之一 C/C学习资源(百度云盘链接) 计算机二级资料(过级专用) C语言学习路线(从入门到实战) 编写C语言程序的7个步骤和编程…...

arm linux应用程序crash分析一般方法
目录: 前言一、定位问题的基本方法论1.1 生产环境下系统崩溃的日志信息示例 二、 分析这类什么都没有的app crash的一般方法论:附录:附录1 pmap -p 进程PID 查看进程的内存分配情况附录2 cat /proc/pid/maps 总结 前言 linux的应用程序app开…...

Web安全防护技术解决方案
1、防止爆破 限制请求ip访问次数,超过设定访问次数后,拒绝访问或锁定N分钟后可再次请求 2、调用短信验证码时 加入验证码采用防爆破策略 3、上传后的文件防止被猜出爬取 保存在物理磁盘可进行加密防护文件不能存储在站点目录,防止通过ur…...
流畅的 Python 第二版(GPT 重译)(十一)
第二十章:并发执行器 抨击线程的人通常是系统程序员,他们心中有着典型应用程序员终其一生都不会遇到的用例。[…] 在 99%的用例中,应用程序员可能会遇到的情况是,生成一堆独立线程并将结果收集到队列中的简单模式就是他们需要了解…...
Blender 3D建模要点
3d模型可以为场景的仿真模拟带来真实感,它还有助于更轻松地识别场景中的所有内容。 例如,如果场景中的所有对象都是简单的形状,如立方体和圆形,则很难在仿真中区分对象。 1、碰撞形状与视觉形状 像立方体和球体这样的简单形状&a…...
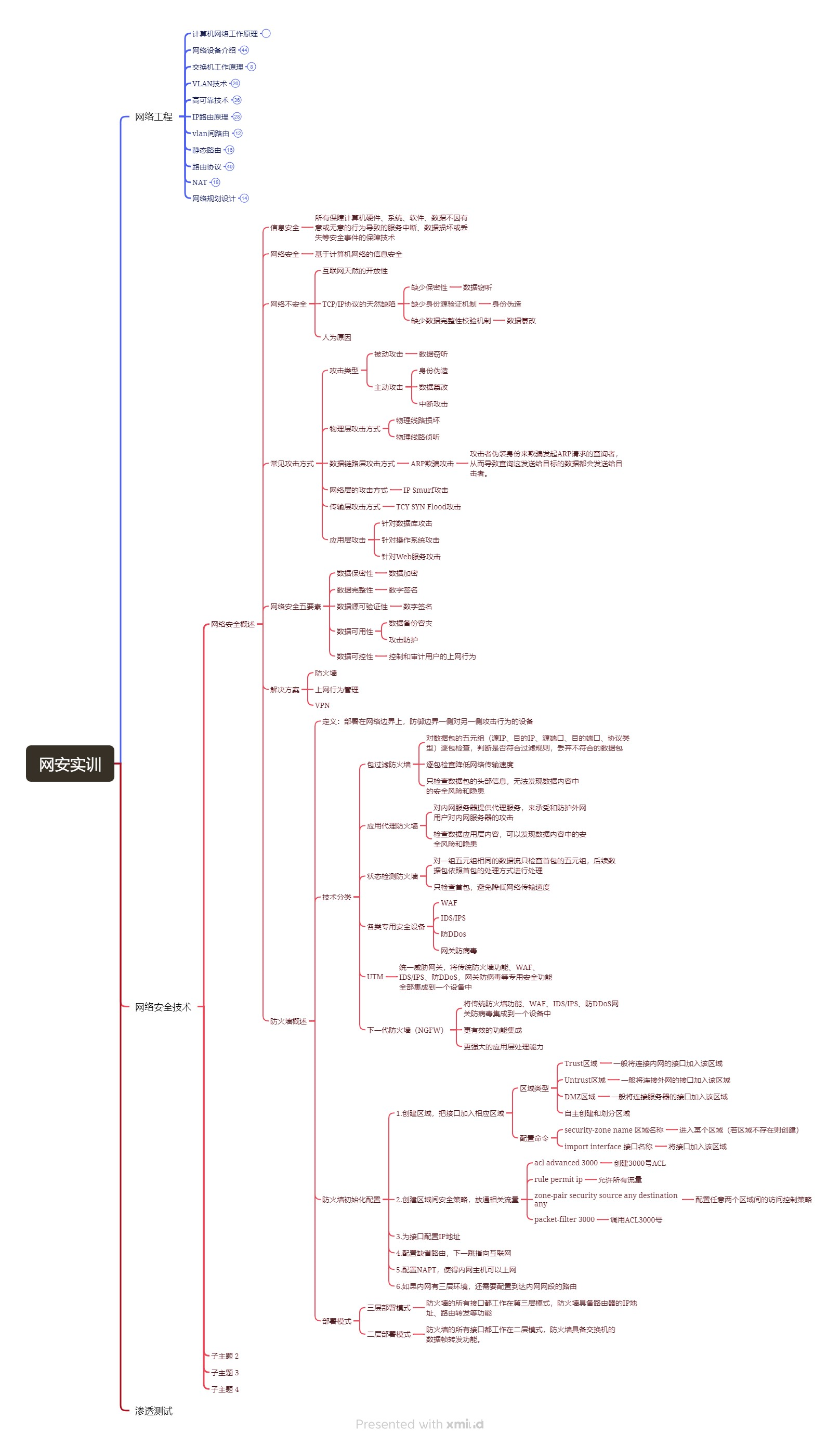
网络安全实训Day8
写在前面 网络工程终于讲完了。这星期到了网络安全技术部分。 网络安全实训-网络安全技术 网络安全概述 信息安全:所有保障计算机硬件、系统、软件、数据不因有意或无意的行为导致的服务中断、数据损坏或丢失等安全事件的保障技术 网络安全:基于计算机…...

GB28181 —— 5、C++编写GB28181设备端,完成将USB摄像头视频实时转发至GB28181服务并可播放(附源码)
被测试的USB摄像头 效果 源码说明 主要功能模拟设备端,完成注册、注销、心跳等,同时当服务端下发指令播放视频时 设备端实时读取USB摄像头视频并通过OpenCV处理后实时转ps格式后封包rtp进行推送给服务端播放。 源码 /****@remark: pes头的封装,里面的具体数据的填写已经占…...
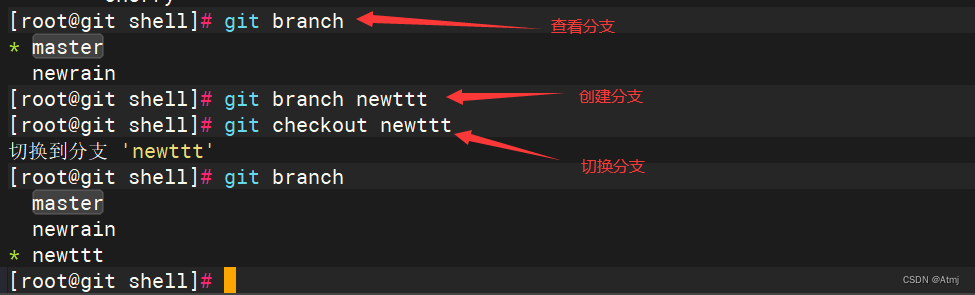
Git工具的详细使用
一、环境说明 [rootgit ~]# getenforce Disabled [rootgit ~]# systemctl status firewalld ● firewalld.service - firewalld - dynamic firewall daemonLoaded: loaded (/usr/lib/systemd/system/firewalld.service; disabled; vendor preset: enabled)Active: inactive (d…...
【prometheus-operator】k8s监控redis
1、准备exporter https://github.com/oliver006/redis_exporter oliver006-redis_exporter-amd64.tar # 安装镜像 docker load -i oliver006-redis_exporter-amd64.tar # 上传镜像 docker tag oliver006/redis_exporter ip/monitor/redis_exporter:latest docker push ip/mo…...

外包干了4年,技术退步明显.......
先说一下自己的情况,大专生,19年通过校招进入杭州某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落! 而我已经在一个企业干了四年的功能测…...

xbackup 备份MySQL数据库脚本
#!/bin/bash ## 方法一:将回车符(\r)替换为换行符(\n) 替换不可见字符 报错问题:shell脚本执行错误 $‘\r‘:command not found ## sed -i s/\r// xtrabackup.sh ## 备份计划任务 ## ## 每天凌晨1:30一次全量备份 ## 每天间隔1小时一次增量备份 ## 30 1 * * * backup…...

npm常用命令详解
npm(Node Package Manager)是Node.js的包管理器,它提供了大量的命令来安装、管理、发布Node.js模块和包。以下是npm常用命令的详解及示例: 1. 查看npm版本 命令:npm -v 示例:npm -v 将输出当前安装的npm版…...
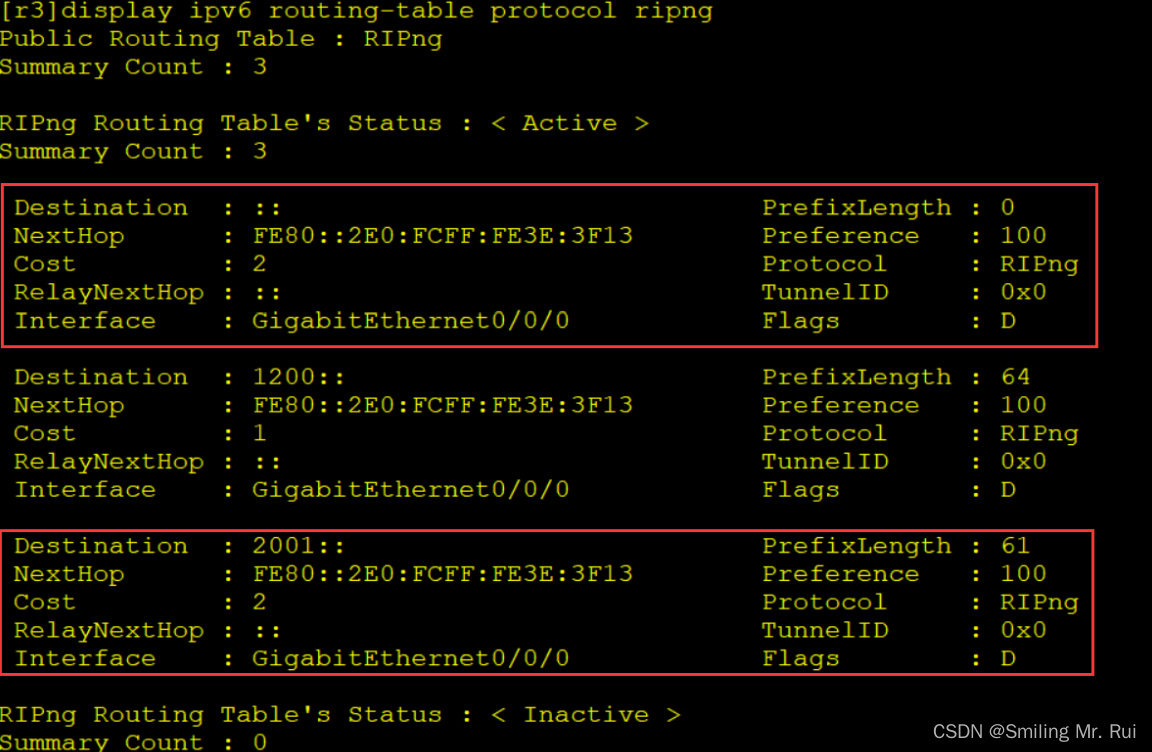
IPV6协议之RIPNG
目录 前言: 一、RIPNG与RIP的区别 二、如何配置RIPNG 如何解决RIPNG环路问题呢? 控制RIPNG的选路 1、修改RIPNG默认优先级 2.配置接口附加开销值从而干涉RIPNG的选路 RIPNG拓展配置 1.RIPNG的认证 配置RIPNG进程下的IPsec认证: 配…...
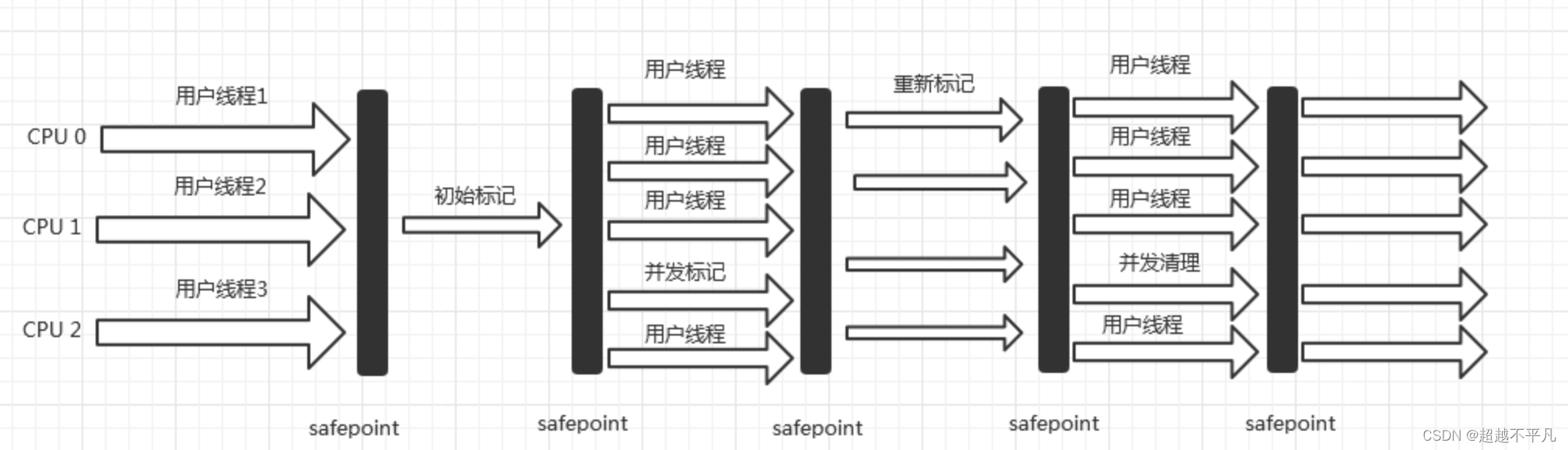
JVM垃圾收集器你会选择吗?
目录 一、Serial收集器 二、ParNew收集器 三、Paralle Scavenge 四、Serial Old 五、Parallel Old 六、CMS收集器 6.1 CMS对处理器资源非常敏感 6.2 CMS容易出现浮动垃圾 6.3 产生内存碎片 七、G1 收集器 八、如何选择合适的垃圾收集器 JVM 垃圾收集器是Java虚…...

游戏防沉迷系统相关内容
网站地址:网络游戏防沉迷实名认证系统 PHP代码: 创建对应文件,在需要的位置get传参请求即可,具体参数参考 网络游戏防沉迷实名认证系统接口对接技术规范v2.0 1、上传信息 <?php $url "https://wlc.nppa.gov.cn/test…...
每日OJ题_牛客_JD1 年终奖(动态规划)
目录 牛客_JD1 年终奖 解析代码 牛客_JD1 年终奖 年终奖_牛客题霸_牛客网 解析代码 #include <vector> class Bonus { public: int getMost(vector<vector<int> > board) {int m board.size(), n board[0].size();vector<vector<int>> dp(m…...
深度学习 tablent表格识别实践记录
下载代码:https://github.com/asagar60/TableNet-pytorch 下载模型:https://drive.usercontent.google.com/download?id13eDDMHbxHaeBbkIsQ7RSgyaf6DSx9io1&exportdownload&confirmt&uuid1bf2e85f-5a4f-4ce8-976c-395d865a3c37 原理&#…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
