c++学习笔记(10)
1.
二分答案是一种常用的算法思想,用于解决一些需要枚举所有可能答案的问题。它的基本思想是将问题的答案范围缩小到一半,然后根据一定的条件判断,再将答案范围缩小到一半,直到找到正确的答案或者确定不存在正确答案为止。
下面以求解一个数的平方根为例,介绍二分答案的实现过程:
-
首先,我们需要确定答案的范围。对于求解一个数的平方根,我们可以将答案范围设为[0, x],其中x是待求的数。
-
然后,我们需要定义一个函数来判断当前的答案是否满足要求。对于求解一个数的平方根,我们可以定义一个函数check(mid),其中mid表示当前的答案,如果mid的平方小于等于x,则返回true,否则返回false。
-
接下来,我们需要使用二分答案的思想来不断缩小答案范围。具体地,我们首先取答案范围的中间值mid=(l+r)/2,然后调用check(mid)函数来判断mid是否满足要求。如果满足要求,说明答案在[l, mid]范围内,因此我们将答案范围更新为[l, mid];否则说明答案在[mid+1, r]范围内,因此我们将答案范围更新为[mid+1, r]。重复这个过程,直到找到正确的答案或者确定不存在正确答案为止。
下面是代码示例:
// 定义了一个findSqrt函数来求解一个数的平方根。
// 该函数接受一个参数x,表示待求的数。
// 在函数内部,使用二分答案的思想来不断缩小答案范围,直到找到正确的答案或者确定不存在正确答案为止。
// 最后,在主函数中读取输入数据并输出结果。#include <iostream>
using namespace std;bool check(double mid, double x) {return mid * mid <= x;
}double findSqrt(double x) {double l = 0, r = x;while (r - l > 1e-6) {double mid = (l + r) / 2;if (check(mid, x)) {l = mid;} else {r = mid;}}return l;
}int main() {double x;cin >> x;cout << findSqrt(x) << endl;return 0;
}2.
向量数组(vector array)是一种数据结构,用于存储多个向量。在C++中,可以使用std::vector类来实现向量数组。
-
定义向量数组:
std::vector<int> arr[N];上述代码定义了一个名为arr的向量数组,其中每个元素都是一个整数类型的向量。
-
添加元素到向量数组中的特定向量:
arr[index].push_back(value);上述代码将值value添加到向量数组中索引为index的向量的末尾。
-
访问向量数组中的特定向量的元素:
int value = arr[index][position];上述代码获取向量数组中索引为index的向量中位置为position的元素的值,并将其赋给变量value。
-
遍历向量数组中的向量:
for (int i = 0; i < N; i++) { for (int j = 0; j < arr[i].size(); j++) { // 处理arr[i][j]的逻辑 } }上述代码使用两个嵌套的循环来遍历向量数组中的每个向量及其元素。外层循环控制向量的索引,内层循环控制向量中的元素位置。
-
获取向量数组的大小:
int size = arr.size();上述代码获取向量数组的大小,即包含的向量的数量。
-
清空向量数组:
arr.clear();上述代码清空整个向量数组,移除所有向量及其元素。
这些是关于C++中向量数组的基本操作和用法。通过使用向量数组,可以方便地管理和操作一组向量,实现灵活的数据存储和操作。
3.
bitset是C++标准库中的一个容器,用于处理固定大小的位序列。它可以用来存储和操作二进制数据,例如位标志、位掩码等。
-
包含头文件:
#include <bitset> -
定义
bitset对象:std::bitset<N> bitset_variable;其中
N是一个整数,表示bitset的大小,即可以存储的位数。 -
初始化
bitset对象:std::bitset<8> b1(0b11001100); // 使用二进制字面值初始化 std::bitset<8> b2("11001100"); // 使用字符串初始化 -
访问
bitset的元素:int index = 3; bool value = bitset_variable[index]; // 获取索引为index的位的值 bitset_variable.set(index, true); // 将索引为index的位设置为true bitset_variable.set(index, false); // 将索引为index的位设置为false -
对
bitset进行位运算:std::bitset<8> b1(0b11001100); std::bitset<8> b2(0b00111100); b1 &= b2; // 按位与运算 b1 |= b2; // 按位或运算 b1 ^= b2; // 按位异或运算 b1 ~= b2; // 按位取反运算 -
输出
bitset的内容:std::cout << bitset_variable << std::endl; // 输出bitset的内容
这些是关于C++中bitset的基本操作和用法。通过使用bitset,可以方便地处理位级别的数据,执行位运算和位操作。
4.
拆位思想是一种常用的位运算技巧,它通过将一个整数的二进制表示拆分成多个部分,然后对每个部分进行独立的操作,最后再将结果合并起来。这种思想在处理一些复杂的位运算问题时非常有用。
-
将一个整数的二进制表示拆分成多个部分:
int num = 23; // 二进制表示为 00010111int part1 = (num >> 4) & 0xF; // 右移4位,得到 00000101int part2 = num & 0xF; // 与0xF进行按位与运算,得到 00000111-
每个部分进行独立的操作:
int result1 = part1 + 1; // 结果为 5int result2 = part2 - 1; // 结果为 7-
将结果合并起来:
int finalResult = (result1 << 4) | result2; // 左移4位,得到 00010100,与result2进行按位或运算,得到 00010111在上述代码中,我们首先将整数num的二进制表示拆分成了两个部分part1和part2。然后,我们对每个部分进行了独立的操作,得到了result1和result2。最后,我们将这两个结果合并起来,得到了最终的结果finalResult。
需要注意的是,拆位思想并不是一种通用的算法,而是针对特定的问题而设计的。在使用拆位思想时,需要根据具体的问题来选择合适的拆分方式和操作方法。
5.
unsigned是C++中用于声明无符号整数类型的关键字。它表示一个非负的整数,其取值范围为0到2^n-1,其中n是该类型的位数。
#include <iostream> int main() { unsigned int num = 4294967295; // 最大的无符号整数 std::cout << "The maximum value of an unsigned int is: " << num << std::endl; return 0;
}需要注意的是,由于无符号整数没有符号位,因此它们的取值范围比有符号整数更大。但是,如果将无符号整数与有符号整数进行比较或运算,可能会导致意外的结果。因此,在使用无符号整数时,需要特别注意类型转换和溢出问题。
6.
深度优先搜索(DFS)是一种用于遍历或搜索树或图的算法。它沿着树的深度遍历树的节点,尽可能深地搜索树的分支。当节点v的所有边都已被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
以下是深度优先搜索的详细解析和代码示例:
-
定义一个栈,用于存储待访问的节点。
-
将起始节点压入栈中。
-
当栈不为空时,弹出栈顶元素,访问该节点。
-
将该节点的所有邻接节点压入栈中。
-
重复步骤3和步骤4,直到栈为空。
以下是深度优先搜索的代码示例:
#include <iostream>
#include <vector>
#include <stack>
using namespace std;// 定义了一个名为dfs的函数,用于实现深度优先搜索。
// 该函数接受三个参数:当前节点、图的邻接表表示和访问标记数组。
// 使用一个栈来存储待访问的节点,并将起始节点压入栈中。
// 然后,循环地弹出栈顶元素,访问该节点,并将其所有邻接节点压入栈中。
// 最后,输出所有被访问过的节点。void dfs(int node, vector<vector<int>>& graph, vector<bool>& visited) {stack<int> s;s.push(node);while (!s.empty()) {int v = s.top();s.pop();if (!visited[v]) {cout << v << " ";visited[v] = true;for (int i = 0; i < graph[v].size(); i++) {if (!visited[graph[v][i]]) {s.push(graph[v][i]);}}}}
}int main() {vector<vector<int>> graph = {{1, 2}, {0, 3}, {0, 3, 4}, {1, 2}, {2}};vector<bool> visited(graph.size(), false);dfs(0, graph, visited);return 0;
}7.
深度优先搜索(DFS)是一种用于遍历或搜索树或图的算法。在实际应用中,我们常常需要对搜索过程进行剪枝,以减少搜索空间和提高效率。剪枝是指在搜索过程中,对于一些不可能产生最优解的分支,直接放弃搜索,从而减少搜索空间。
以下是深度优先搜索剪枝的详细解析和代码示例:
-
定义一个栈,用于存储待访问的节点。
-
将起始节点压入栈中。
-
当栈不为空时,弹出栈顶元素,访问该节点。
-
判断该节点是否满足剪枝条件,如果满足,则跳过该节点,否则继续搜索。
-
将该节点的所有邻接节点压入栈中。
-
重复步骤3和步骤4,直到栈为空。
代码示例:
#include <iostream>
#include <vector>
#include <stack>
using namespace std;bool isPruned(int node) {// 剪枝条件判断return false;
}void dfs(int node, vector<vector<int>>& graph, vector<bool>& visited) {stack<int> s;s.push(node);while (!s.empty()) {int v = s.top();s.pop();if (!visited[v]) {cout << v << " ";visited[v] = true;for (int i = 0; i < graph[v].size(); i++) { // 判断当前节点是否满足剪枝条件,如果满足,则跳过该节点,否则继续搜索if (!visited[graph[v][i]] && !isPruned(graph[v][i])) {s.push(graph[v][i]);}}}}
}int main() {vector<vector<int>> graph = {{1, 2}, {0, 3}, {0, 3, 4}, {1, 2}, {2}};vector<bool> visited(graph.size(), false);dfs(0, graph, visited);return 0;
}相关文章:
)
c++学习笔记(10)
1. 二分答案是一种常用的算法思想,用于解决一些需要枚举所有可能答案的问题。它的基本思想是将问题的答案范围缩小到一半,然后根据一定的条件判断,再将答案范围缩小到一半,直到找到正确的答案或者确定不存在正确答案为止。 下面…...

Visual Studio - 添加快捷键图标
Visual Studio - 添加快捷键图标 1. Text Editor Toolbar Options -> Add or Remove Buttons -> Customize2. Toolbars3. Commands -> Debug4. Add Command...References 1. Text Editor Toolbar Options -> Add or Remove Buttons -> Customize 2. Toolbars B…...

突破边界:Web3开启数字化社会的新纪元
引言 随着科技的不断进步和数字化社会的发展,Web3正逐渐成为了人们关注的焦点。作为新一代互联网的演进形态,Web3具有突破传统边界、实现去中心化的特点,被认为将开启数字化社会的新纪元。本文将深入探讨Web3的概念、特点、应用场景…...
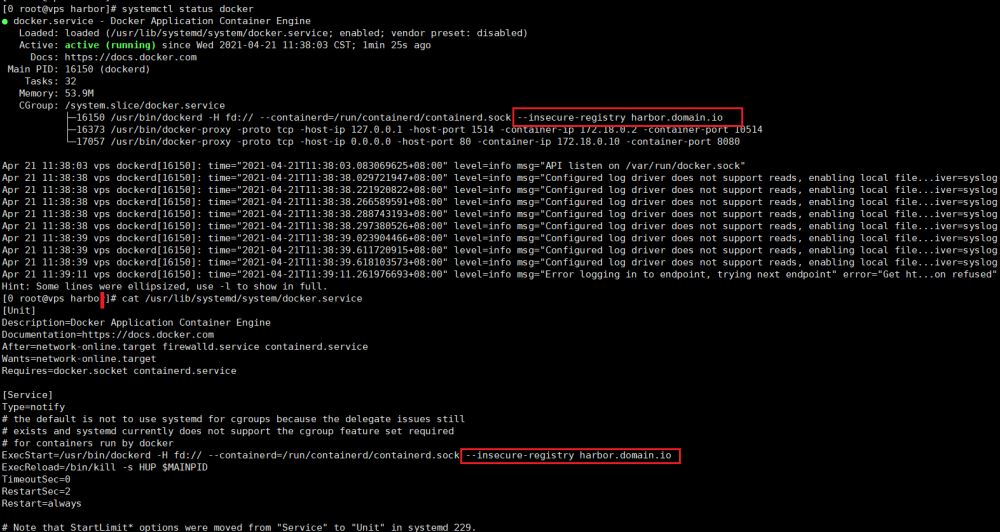
docker仓库登录及配置insecure-registries的方法
docker仓库登录及配置insecure-registries的方法 这篇文章主要介绍了docker仓库登录配置insecure-registries的方法,docker客户端如果配置中添加了insecure-registary配置,就不需要在docker 客户端配置上对应证书,如果不配置要在/etc/docker/certs.d/目…...

Lambda函数与Selenium WebDriverWait类一起使用
Lambda函数是一种匿名函数,也称为内联函数或者lambda表达式。它们在Python中用于创建简短的、一次性的函数。Lambda函数通常用于在代码中传递函数作为参数,或者在需要一个简单的函数,但不想正式定义一个函数的情况下使用。 Lambda函数的特点…...

V R元宇宙平台的未来方向|V R主题馆加 盟|游戏体验馆
未来,VR元宇宙平台可能会呈现出以下发展趋势和可能性: 全面融合现实与虚拟世界: VR元宇宙平台将更加无缝地融合现实世界和虚拟世界,用户可以在虚拟环境中进行各种活动,与现实世界进行互动,并且体验到更加逼…...

sox命令用法
play input.wav 播放音频 sox input.wav -n stat 查看音频文件信息 soxi input.wav 查看音频文件信息input sox input.wav -n stat -v 不失真最大调整量 sox -v 0.8 input.wav output.wav 调整音量0.8,(大于1为扩大,小于1为缩小) sox *.wav *…...

Android kotlin全局悬浮窗全屏功能和锁屏页面全屏悬浮窗功能二
1.前言 在进行app应用开发中,在实现某些功能中要求实现悬浮窗功能,分为应用内悬浮窗 ,全局悬浮窗和 锁屏页面悬浮窗功能 等,接下来就来实现这些悬浮窗全屏功能,首选看下第二部分功能实现 2.kotlin实现锁屏页面悬浮窗全屏功能二分析 悬浮窗是属于Android系统的一种浮动窗…...
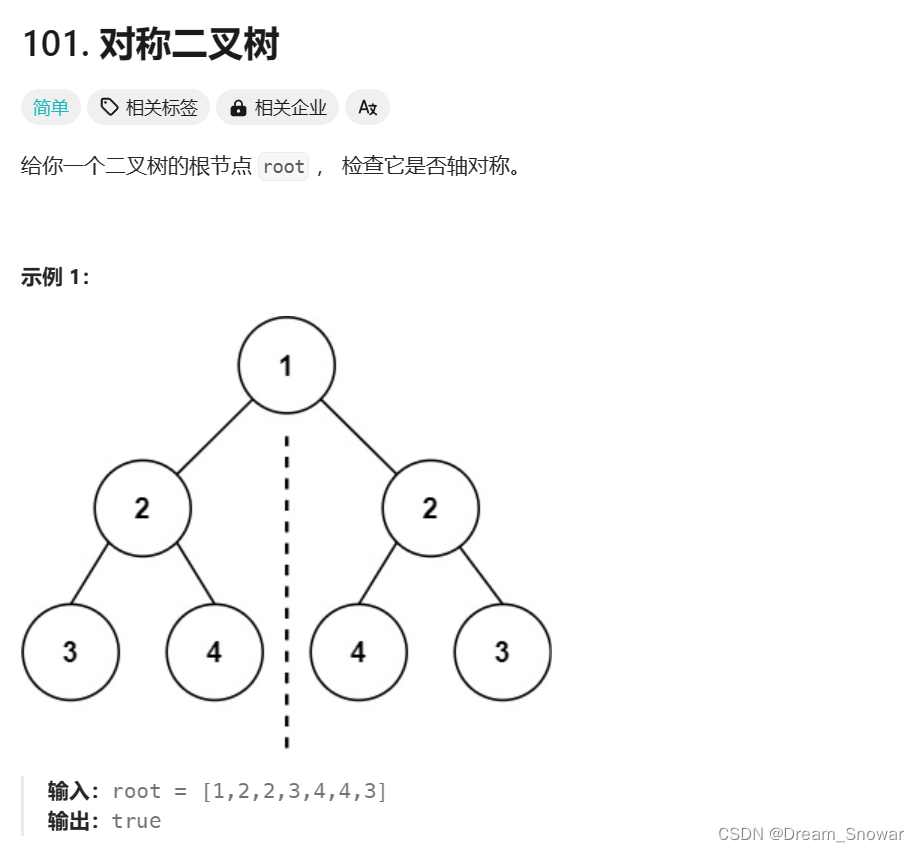
[数据结构]二叉树与递归OJ
上回我们手撕了一棵二叉树,并且通过递归完成了遍历,这回我们将深入理解用递归解决相关的二叉树问题,数量使用分治的思想. 上回的代码: #include<stdio.h> #include<stdlib.h> typedef struct BinTreeNode {struct BinTreeNode* left;struct BinTreeNode* right;i…...
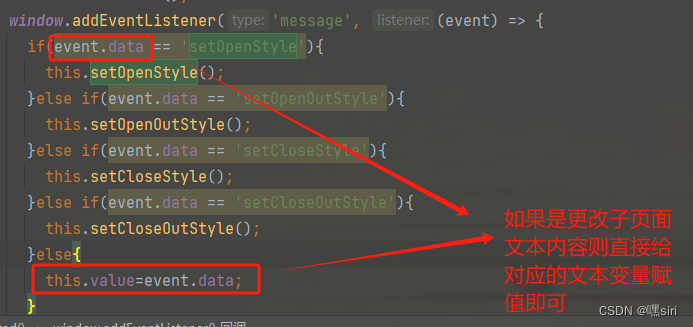
vue iframe实现父页面实时调用子页面方法和内容,已解决
父页面标签添加鼠标按下事件 父页方法中建立iframe通信 实时调用子页面方法 实时更改子页面文本内容...
Spring Cloud Gateway教程
1 微服务网关概述 Spring Cloud Gateway是在 Spring 生态系统之上构建的API网关服务,旨在为微服务架构应用提供一种简单有效的统一的API路由管理方式。 Spring Cloud Gateway主要功能: 反向代理认证鉴权流量控制熔断日志监控 2 Spring Cloud Gateway三…...
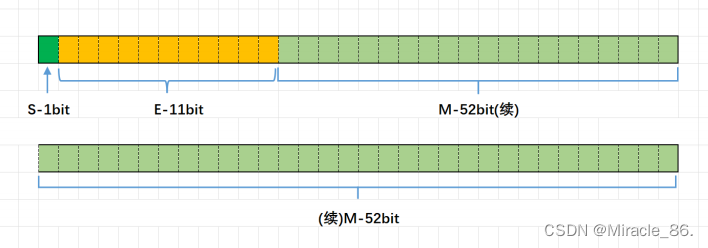
解码新时代内存架构:探秘数据在内存中的灵动驻足
欢迎来到白刘的领域 Miracle_86.-CSDN博客 系列专栏 C语言知识 先赞后看,已成习惯 创作不易,多多支持! 随着信息技术的飞速发展,我们身处一个数据爆炸的时代。数据的处理和存储方式正日益成为技术革新的重要领域。在新时代的…...
前端基础篇-前端工程化 Vue 项目开发流程(环境准备、Element 组件库、Vue 路由、项目打包部署)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 环境准备 1.1 安装 NodeJs 1.2 验证 NodeJs 环境变量 1.3 配置 npm 的全局安装路径 1.4 切换 npm 的淘宝镜像( npm 使用国内淘宝镜像的方法(最新) ) 1.5 查看镜像…...
】)
【通用人工智能AGI元年-各领域的精彩AI/LLM(持续更新)】
AI元年弄潮儿 通用人工智能AGI时代大模型LLM集成平台:Poe语言大模型:ChatGPT音乐:Suno文生图: [Stable Diffusion整合包](https://www.bilibili.com/video/BV1iM4y1y7oA/?spm_id_from333.999.0.0&vd_source260c69efcf1f56243…...

【微服务】设计弹性微服务架构模式
目录 模式#1 — 超时模式#2 — 重试模式#3— 隔离模式#4— 断路器模式#5 — 冗余推荐超级课程: Docker快速入门到精通Kubernetes入门到大师通关课AWS云服务快速入门实战在微服务架构中,服务通常相互协作以提供业务用例。这些服务可能在可用性、可伸缩性、弹性等方面具有…...

Websocket + Vue使用
这里有一篇文档可以参考一下> 闪现 POM文件 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId><version>2.7.0</version> </dependency> WebSocketConf…...

AI程序员革命:探析Devin的登场与编程未来
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

vue 控制窗口禁止缩放,已解决
注意:不是浏览器窗口禁止缩放 1.vue框架中,index.html文件head标签中加上内容 <meta name"viewport" content"widthdevice-width, initial-scale1, maximum-scale1, user-scalable0"><script>document.addEventListen…...
【黑马头条】-day01环境搭建SpringBoot-Cloud-Nacos
文章目录 1 环境搭建及简介2 项目介绍2.1 应用2.2 业务说明2.3 技术栈2.4 收获2.5 大纲 3 Nacos准备3.1 安装Nacos 4 初始工程搭建4.1 环境准备4.1.1 导入项目4.1.2 设置本地仓库4.1.3 设置项目编码格式 4.2 全局异常4.2.1 自动装配 4.3 工程主体结构 5 登录功能开发5.1 需求分…...

HTML发展史
为什么要讲 HTML 发展史呢? 唐太宗告诉我们: 以铜为镜,可以正衣冠;以史为镜,可以知兴替;以人为镜,可以明得失。 那了解了 HTML 的发展史,可以知道什么呢? 答案是兼容 国内在 淘宝…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...
