【Leetcode每日一题】 动态规划 - 使用最小花费爬楼梯(难度⭐)(41)
1. 题目解析
题目链接:746. 使用最小花费爬楼梯

这个问题的理解其实相当简单,只需看一下示例,基本就能明白其含义了。
2.算法原理
一、设定状态表
为了解决这个问题,我们首先要明确一个“状态表”。这个状态表其实就是一个记录表,用来记录到达每一层楼时的最小花费。
我们设定dp[i]为到达第i层楼时的最小花费。注意,这里的dp[i]只表示到达第i层时的花费,并不包括在第i层本身需要支付的费用。
二、考虑状态转移
接下来,我们要思考如何从一层楼到达另一层楼,并计算出最小花费。
-
从第
i-1层上来:如果我们从第i-1层爬上来,那么到达第i层的总花费就是dp[i-1] + cost[i-1],其中cost[i-1]是第i-1层的费用。 -
从第
i-2层上来:另一种可能的情况是我们从第i-2层直接跳到第i层(假设有这样的跳跃能力)。那么到达第i层的总花费就是dp[i-2] + cost[i-2]。
我们需要比较这两种情况,选择花费更小的那种方式。
三、初始化状态
在开始计算之前,我们需要给状态表一个起点。显然,站在第一层或第二层是不需要花费的,所以dp[0] = dp[1] = 0。
四、填表顺序
按照我们前面讨论的状态转移过程,我们需要从左往右依次计算每一层的最小花费,直到最后一层。
五、得出结果
最后,当我们填满整个状态表后,dp[n]就代表了到达最顶层的最小花费,这就是我们要求的答案。
3.代码编写
class Solution
{
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> dp(n + 1);for(int i = 2; i <= n; i++)dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2]+ cost[i - 2]);return dp[n];}
};The Last
嗯,就是这样啦,文章到这里就结束啦,真心感谢你花时间来读。
觉得有点收获的话,不妨给我点个赞吧!
如果发现文章有啥漏洞或错误的地方,欢迎私信我或者在评论里提醒一声~
相关文章:

【Leetcode每日一题】 动态规划 - 使用最小花费爬楼梯(难度⭐)(41)
1. 题目解析 题目链接:746. 使用最小花费爬楼梯 这个问题的理解其实相当简单,只需看一下示例,基本就能明白其含义了。 2.算法原理 一、设定状态表 为了解决这个问题,我们首先要明确一个“状态表”。这个状态表其实就是一个记录…...

Springboot旅游管理系统设计与实现
** 🍅点赞收藏关注 → 私信领取本源代码、数据库🍅 本人在Java毕业设计领域有多年的经验,陆续会更新更多优质的Java实战项目,希望你能有所收获,少走一些弯路。🍅关注我不迷路🍅** 一、研究背景…...
)
c++学习笔记(10)
1. 二分答案是一种常用的算法思想,用于解决一些需要枚举所有可能答案的问题。它的基本思想是将问题的答案范围缩小到一半,然后根据一定的条件判断,再将答案范围缩小到一半,直到找到正确的答案或者确定不存在正确答案为止。 下面…...

Visual Studio - 添加快捷键图标
Visual Studio - 添加快捷键图标 1. Text Editor Toolbar Options -> Add or Remove Buttons -> Customize2. Toolbars3. Commands -> Debug4. Add Command...References 1. Text Editor Toolbar Options -> Add or Remove Buttons -> Customize 2. Toolbars B…...

突破边界:Web3开启数字化社会的新纪元
引言 随着科技的不断进步和数字化社会的发展,Web3正逐渐成为了人们关注的焦点。作为新一代互联网的演进形态,Web3具有突破传统边界、实现去中心化的特点,被认为将开启数字化社会的新纪元。本文将深入探讨Web3的概念、特点、应用场景…...
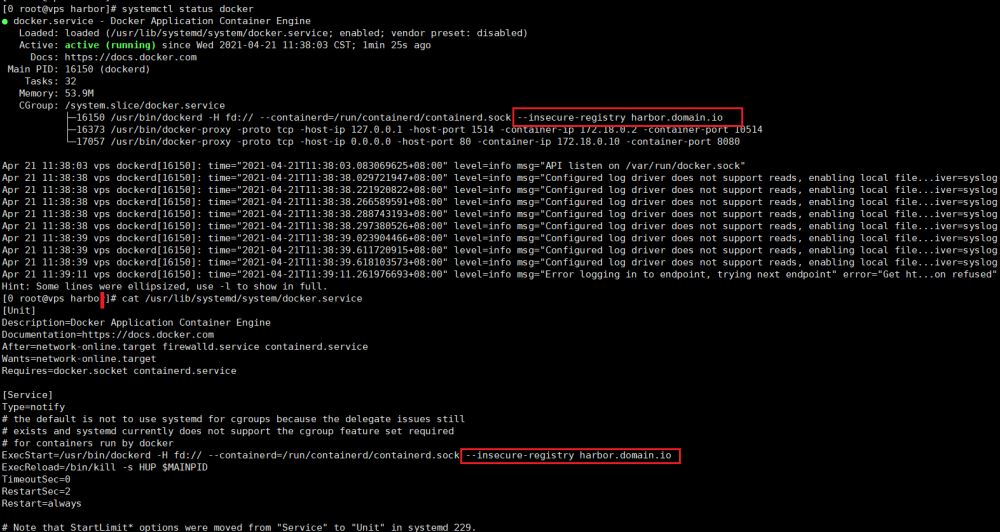
docker仓库登录及配置insecure-registries的方法
docker仓库登录及配置insecure-registries的方法 这篇文章主要介绍了docker仓库登录配置insecure-registries的方法,docker客户端如果配置中添加了insecure-registary配置,就不需要在docker 客户端配置上对应证书,如果不配置要在/etc/docker/certs.d/目…...

Lambda函数与Selenium WebDriverWait类一起使用
Lambda函数是一种匿名函数,也称为内联函数或者lambda表达式。它们在Python中用于创建简短的、一次性的函数。Lambda函数通常用于在代码中传递函数作为参数,或者在需要一个简单的函数,但不想正式定义一个函数的情况下使用。 Lambda函数的特点…...

V R元宇宙平台的未来方向|V R主题馆加 盟|游戏体验馆
未来,VR元宇宙平台可能会呈现出以下发展趋势和可能性: 全面融合现实与虚拟世界: VR元宇宙平台将更加无缝地融合现实世界和虚拟世界,用户可以在虚拟环境中进行各种活动,与现实世界进行互动,并且体验到更加逼…...

sox命令用法
play input.wav 播放音频 sox input.wav -n stat 查看音频文件信息 soxi input.wav 查看音频文件信息input sox input.wav -n stat -v 不失真最大调整量 sox -v 0.8 input.wav output.wav 调整音量0.8,(大于1为扩大,小于1为缩小) sox *.wav *…...

Android kotlin全局悬浮窗全屏功能和锁屏页面全屏悬浮窗功能二
1.前言 在进行app应用开发中,在实现某些功能中要求实现悬浮窗功能,分为应用内悬浮窗 ,全局悬浮窗和 锁屏页面悬浮窗功能 等,接下来就来实现这些悬浮窗全屏功能,首选看下第二部分功能实现 2.kotlin实现锁屏页面悬浮窗全屏功能二分析 悬浮窗是属于Android系统的一种浮动窗…...
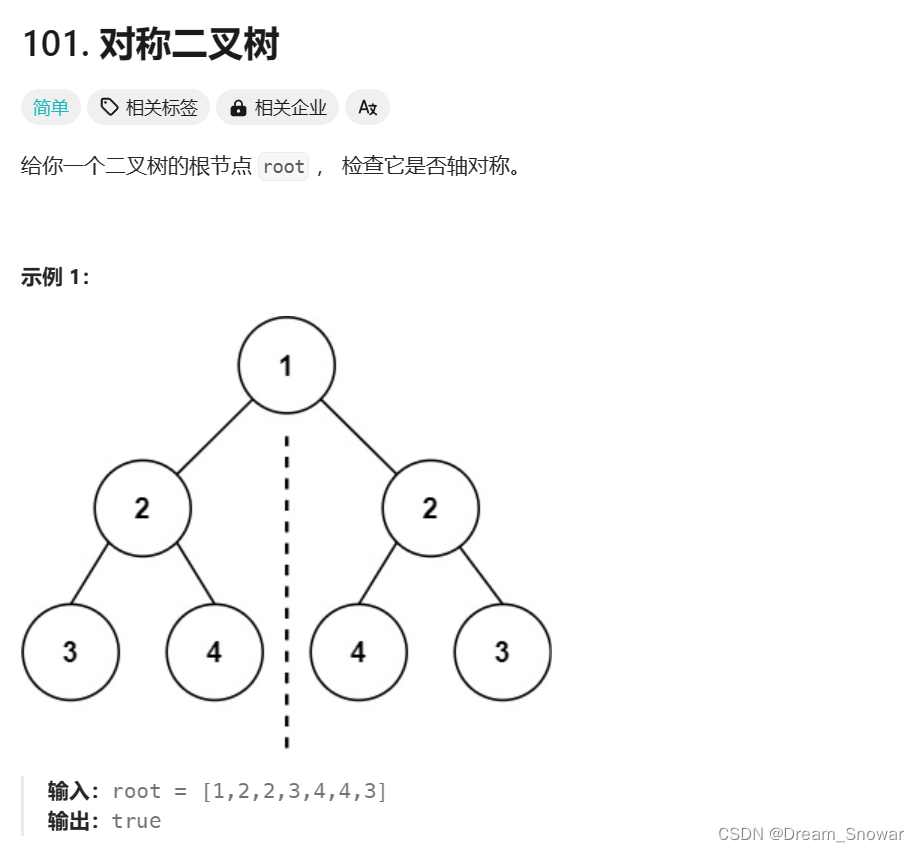
[数据结构]二叉树与递归OJ
上回我们手撕了一棵二叉树,并且通过递归完成了遍历,这回我们将深入理解用递归解决相关的二叉树问题,数量使用分治的思想. 上回的代码: #include<stdio.h> #include<stdlib.h> typedef struct BinTreeNode {struct BinTreeNode* left;struct BinTreeNode* right;i…...
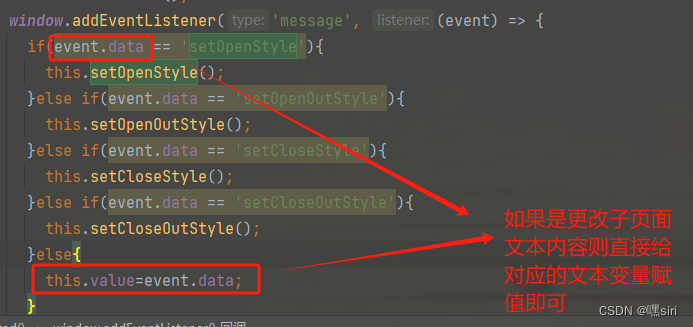
vue iframe实现父页面实时调用子页面方法和内容,已解决
父页面标签添加鼠标按下事件 父页方法中建立iframe通信 实时调用子页面方法 实时更改子页面文本内容...
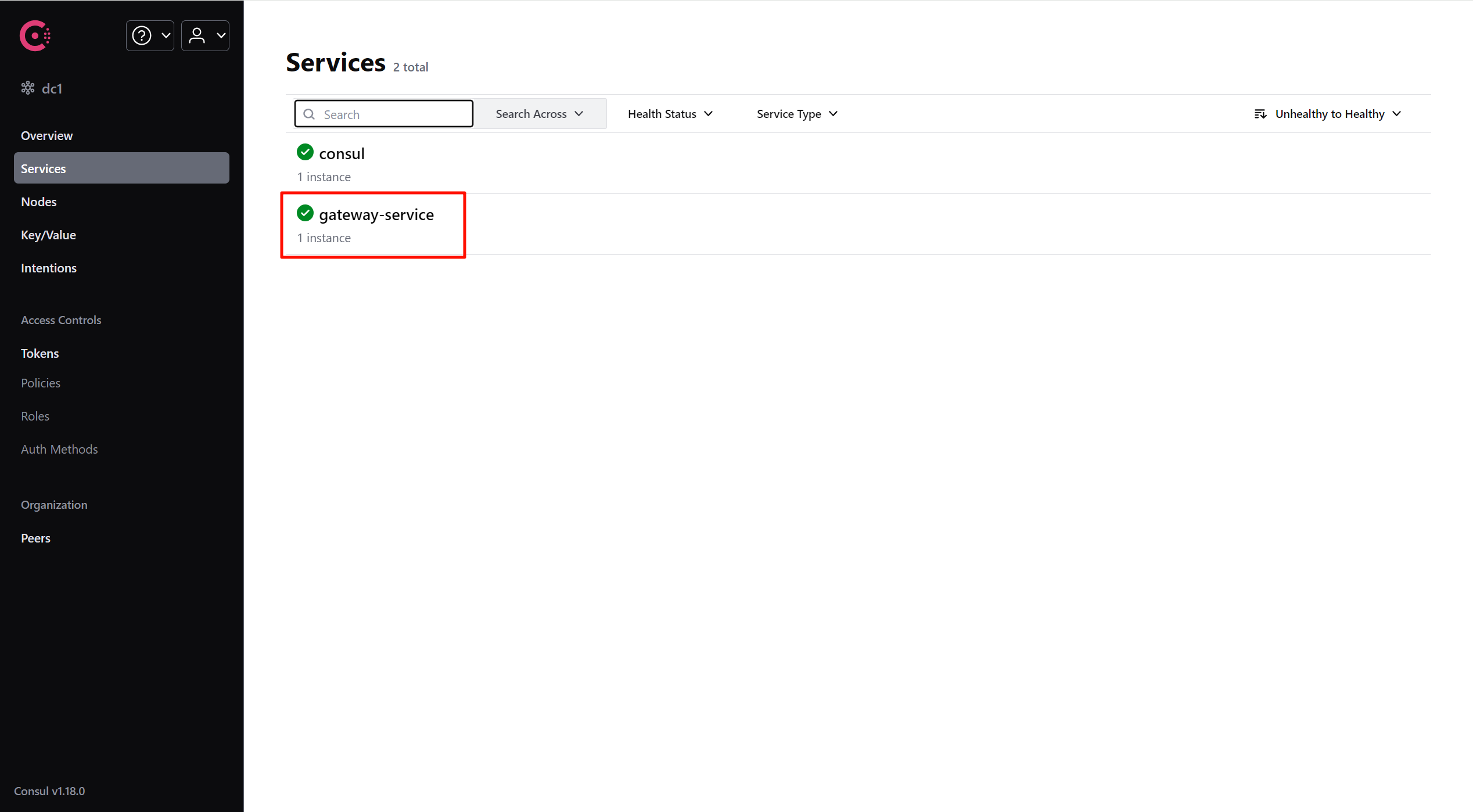
Spring Cloud Gateway教程
1 微服务网关概述 Spring Cloud Gateway是在 Spring 生态系统之上构建的API网关服务,旨在为微服务架构应用提供一种简单有效的统一的API路由管理方式。 Spring Cloud Gateway主要功能: 反向代理认证鉴权流量控制熔断日志监控 2 Spring Cloud Gateway三…...
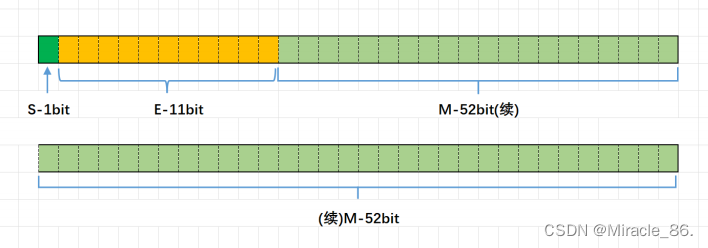
解码新时代内存架构:探秘数据在内存中的灵动驻足
欢迎来到白刘的领域 Miracle_86.-CSDN博客 系列专栏 C语言知识 先赞后看,已成习惯 创作不易,多多支持! 随着信息技术的飞速发展,我们身处一个数据爆炸的时代。数据的处理和存储方式正日益成为技术革新的重要领域。在新时代的…...
前端基础篇-前端工程化 Vue 项目开发流程(环境准备、Element 组件库、Vue 路由、项目打包部署)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 环境准备 1.1 安装 NodeJs 1.2 验证 NodeJs 环境变量 1.3 配置 npm 的全局安装路径 1.4 切换 npm 的淘宝镜像( npm 使用国内淘宝镜像的方法(最新) ) 1.5 查看镜像…...
】)
【通用人工智能AGI元年-各领域的精彩AI/LLM(持续更新)】
AI元年弄潮儿 通用人工智能AGI时代大模型LLM集成平台:Poe语言大模型:ChatGPT音乐:Suno文生图: [Stable Diffusion整合包](https://www.bilibili.com/video/BV1iM4y1y7oA/?spm_id_from333.999.0.0&vd_source260c69efcf1f56243…...

【微服务】设计弹性微服务架构模式
目录 模式#1 — 超时模式#2 — 重试模式#3— 隔离模式#4— 断路器模式#5 — 冗余推荐超级课程: Docker快速入门到精通Kubernetes入门到大师通关课AWS云服务快速入门实战在微服务架构中,服务通常相互协作以提供业务用例。这些服务可能在可用性、可伸缩性、弹性等方面具有…...

Websocket + Vue使用
这里有一篇文档可以参考一下> 闪现 POM文件 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId><version>2.7.0</version> </dependency> WebSocketConf…...

AI程序员革命:探析Devin的登场与编程未来
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

vue 控制窗口禁止缩放,已解决
注意:不是浏览器窗口禁止缩放 1.vue框架中,index.html文件head标签中加上内容 <meta name"viewport" content"widthdevice-width, initial-scale1, maximum-scale1, user-scalable0"><script>document.addEventListen…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
