第十四届蓝桥杯大赛软件赛省赛Java大学B组
最近正在备考蓝桥杯,报的java b组,顺便更一下蓝桥的
幸运数字
题目

思路:填空题,暴力即可
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {static int trans(int x, int y){int res = 0;while(x > 0){res += x % y; // 不用求出转换后的数字,求和即可x /= y; }return res;}public static void main(String[] args) {int i = 0, j = 0;while(i < 2023){j++;if(j % trans(j, 2) == 0 && j % trans(j, 8) == 0 &&j % trans(j, 10) == 0 && j % trans(j, 16) == 0) i++;}System.out.println(j);}
}数组分割
题目

思路:数学题。
1.加起来的总和为奇数时(有奇数个奇数)显然不可能完成分割.
2.全为偶数(n个偶数):中0个元素:
,
中1个元素:
... 所以分法总数为
(二项式定理,不证明了,想了解的可以网上查一下)。
3.偶数个奇数和偶数(2m个奇数,n个偶数):不妨将2m个奇数看成m个偶数计算,有,而偶数的排法为
个,一共
,即2的偶数个数加奇数个数-1次方
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {static final int mod = (int)1e9 + 7;static int even = 0, odd = 0;static int fun(){ if(odd % 2 == 1) return 0; // 奇数个奇数,无法排if(odd == 0) return quick_pow(2, even); // 0个奇数,2^偶数个数return quick_pow(2, odd - 1 + even); // 奇数个数加偶数个数减1}static int quick_pow(int a, int b){int res = 1;for(; b > 0; b >>= 1){if((b & 1) == 1) res = (int)((long)res * a % mod);a = (int)((long)a * a % mod);}return res;}public static void main(String[] args) {Scanner scan = new Scanner(System.in);int t = scan.nextInt();while(t-- > 0){int n = scan.nextInt();even = 0; odd = 0;for(int i = 0; i < n; i++) {int a = scan.nextInt();if(a % 2 == 1) odd ++;else even ++;}System.out.println(fun());}scan.close();}
}矩形总面积
题目

思路:数学题
只要两个矩形有相交区域,一定满足
相交区域面积=(min(x2,x4)-max(x1,x3))*(min(y2,y4) - max(x1,x3)。
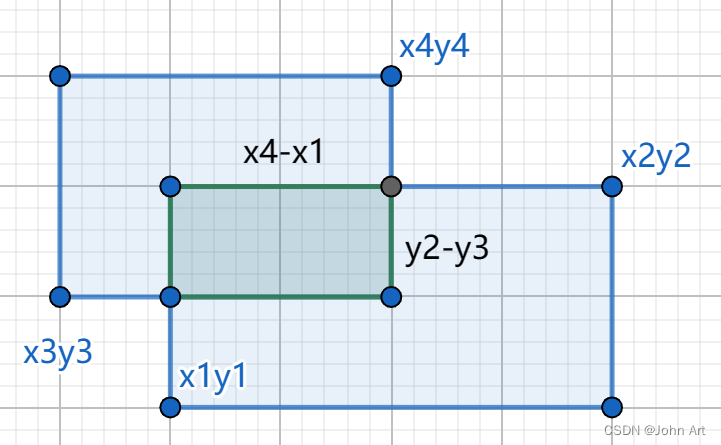
不会证明,但是是对的...(也许可以列出所有的情况证明但是有点麻烦,懒得证了)。
这道题还有个小坑,10^10会爆int,因此用long存面积。读题仔细一点就ok。
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int x1 = scan.nextInt(); int y1 = scan.nextInt();int x2 = scan.nextInt(); int y2 = scan.nextInt();int x3 = scan.nextInt(); int y3 = scan.nextInt();int x4 = scan.nextInt(); int y4 = scan.nextInt();// 总面积long ans = (long)(y2 - y1) * (x2 - x1) + (y4 - y3) * (x4 - x3);// 不相交,不减,相交,减去相交面积if(x2 < x3 || x4 < x1 || y3 > y2 || y1 > y4) System.out.println(ans);else System.out.println(ans - (long)((Math.min(y2, y4) - Math.max(y1, y3))* (Math.min(x2, x4) - Math.max(x1, x3))));scan.close();}
}蜗牛
题目

思路:dp
f[i][0]:到达第i根竹竿底部的最短用时 f[i][1]:到达第i根竹竿上传送门的最短用时
从第i点去i+1点:
底部:1.从i进入传送门,i+1出来,往下爬。 2.从i底部直接爬到i+1底部
传送门入口:1.从i进入传送门,i+1出来,往传送门爬(可能往上或下) 2.从i底部直接爬到i+1底部,再往上爬到传送门入口。
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {static final int N = 100010;static int n;static int[] x = new int[N], a = new int[N], b = new int[N];static double[][] f = new double[N][2];public static void main(String[] args) {Scanner scan = new Scanner(System.in);n = scan.nextInt();for(int i = 1; i <= n; i++) x[i] = scan.nextInt();for(int i = 1; i < n; i++){a[i] = scan.nextInt();b[i + 1] = scan.nextInt();}f[1][0] = x[1];f[1][1] = x[1] + a[1] / 0.7;for(int i = 2; i <= n; i++){// 从下面走或者走传送门f[i][0] = Math.min(f[i - 1][0] + x[i] - x[i - 1], f[i - 1][1] + b[i] / 1.3);// 如果传送门出口在入口上面,往上,否则往下,或者直接走下面if(a[i] > b[i]) f[i][1] = Math.min(f[i - 1][0] + x[i] - x[i - 1] + a[i] / 0.7, f[i - 1][1] + (a[i] - b[i]) / 0.7);else f[i][1] = Math.min(f[i - 1][0] + x[i] - x[i - 1] + a[i] / 0.7, f[i - 1][1] + (b[i] - a[i]) / 1.3);}System.out.println(String.format("%.2f", f[n][0]));scan.close();}
}合并区域
题目

思路:dfs + 暴力
思路很简单,但是我估计大家都懒得写(
把地A和读入,旋转3次全部存入数组中,B同理。然后列出两块地的所有位置可能,dfs一下就ok
import java.util.*;
public class Main {static final int N = 60;static int n;static char[][][] A = new char[4][N][N], B = new char[4][N][N];static char[][] M = new char[3 * N][2 * N]; // M储存每种排列方式static int[] dx = {-1, 1, 0, 0}, dy = {0, 0, -1, 1};static void readAndFillArray(Scanner scan, int n, char[][][] array) {for (int i = 0; i < n; i++)for (int j = 0; j < n; j++) { // 读入4种旋转char val = (char) (scan.nextInt() + '0');array[0][i][j] = val;array[1][j][n - 1 - i] = val;array[2][n - 1 - i][n - 1 - j] = val;array[3][n - 1 - j][i] = val;}}static int solve() {int res = 0;for (int i = 0; i < M.length; i++)for (int j = 0; j < M[i].length; j++)if (M[i][j] == '1') // 每找到一个为1的点就dfsres = Math.max(res, dfs(i, j, 0));return res;}static int dfs(int i, int j, int cnt) {if (i < 0 || i >= M.length || j < 0 || j >= M[i].length || M[i][j] == '0')return cnt; // 边界返回M[i][j] = '0'; cnt++;for(int k = 0; k < 4; k++) cnt = dfs(i + dx[k], j + dy[k], cnt);return cnt;}public static void main(String[] args) {Scanner scan = new Scanner(System.in);n = scan.nextInt(); int move = 2 * n - 1;readAndFillArray(scan, n, A);readAndFillArray(scan, n, B);int max = 0;for(int a = 0; a < 4; a++) // A旋转for(int b = 0; b < 4; b++) // B旋转for(int m = 0; m < move; m++) {// M归零防止上一次结果影响for(int i = 0; i < 3 * n; i++) Arrays.fill(M[i], '0');for(int i = 0; i < n; ++i) {// A,B放入MSystem.arraycopy(A[a][i], 0, M[n - 1 + i], 0, n);System.arraycopy(B[b][i], 0, M[m + i], n, n);}max = Math.max(max, solve());}System.out.println(max);scan.close();}
}
买二赠一
题目
思路:双指针
从贵的往便宜的买,买两个后找到能免费的最贵的物品,重复此操作即可
import java.util.*;
import java.io.*;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {static final int N = 500010;static int n;static int[] a = new int[N];static boolean[] st = new boolean[N];public static void main(String[] args) throws IOException {// 数据量比较大,用BufferedReader读入BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));n = Integer.parseInt(reader.readLine());String[] str = reader.readLine().split(" ");for(int i = 0; i < n; i++) a[i] = Integer.parseInt(str[i]);// 从小到大排序,从后往前取,先买贵的Arrays.sort(a, 0, n);// i买的,j送的,count记录买第几个,free表示免费最高价格int i = n, j = n, count = 0, free = 0;long ans = 0;while(j >= 0) {if(count != 2) { // 没买两个,不送count++;do i--; while(i >= 0 && st[i]); // 已经买过/送过的不能再买/送了if(i < 0) break;st[i] = true; // 没买/送,买它!ans += a[i];free = a[i] / 2; // 从大往小取,取到的第二个一定是便宜的物品}else {count = 0;do j--; while(j >= 0 && (st[j] || a[j] > free)); // 已经买过/送过的不能再买/送了,并且价格要小于free才能送if(j < 0) break; // 不满足送东西的要求了st[j] = true;}}for(i = 0; i < n; i++) // 还没买的全给它买了if(!st[i]) ans += a[i];System.out.println(ans);reader.close();}
}合并石子
题目

思路:dp
在二维数组基础上多加一维表示石子颜色,我们可以直接枚举三个状态,当左右都合法时,我们就可以合并两堆石子,也就是dp(i1,j1,k)和dp[i2,j2,k]都合法就可以合并两个区间
注意,我们此时跑完区间(l,r)得到的num(l,r)跟cost(l,r)不一定是最小的,
我们还要再跑一次循环,得到最小的堆数和价值
import java.util.*;public class Main {static final int N = 310, MAX = Integer.MAX_VALUE;static int n;static int[][][] dp = new int[N][N][3]; //dp[i][j][c] 表示从i到j且颜色为c的石碓合并后所花费的最小石头数static int[] sum = new int[N]; //sum[i] 表示从第1堆到第i堆的石头数之和static int[][] num = new int[N][N]; //num[i][j] 表示从i到j合并后的最小堆数 ,即第一个输出答案static int[][] cost = new int[N][N]; //cost[i][j] 表示从i到j合并后的所花费的最小石头数,即第二个输出答案public static void main(String[] args) {Scanner scan = new Scanner(System.in);n = scan.nextInt();for (int i = 1; i <= n; i++) {for (int j = i; j <= n; j++) {num[i][j] = j - i + 1; //初始化从i到j的堆数和Arrays.fill(dp[i][j], MAX); //全部石碓初始化为maxValue方便判断}}for (int i = 1; i <= n; i++) // 用前缀和计算合并的花费sum[i] = sum[i - 1] + scan.nextInt();for (int i = 1; i <= n; i++)dp[i][i][scan.nextInt()] = 0; // 初始化存在的石碓// i,len表示本次排i到i+len的石子,令j=i+len只是为了减少代码长度for (int len = 1; len < n; len++) {for (int i = 1; i + len <= n; i++) {int j = i + len;for (int c = 0; c < 3; c++) { //三种颜色int min = MAX;for (int k = i; k < j; k++)//判断两堆石碓是否合法存在,如果值为maxValue,则表示不存在;只有两堆都存在才能合并if (dp[i][k][c] != MAX && dp[k + 1][j][c] != MAX)min = Math.min(min, dp[i][k][c] + dp[k + 1][j][c] + sum[j] - sum[i - 1]);if (min != MAX) {dp[i][j][(c + 1) % 3] = Math.min(dp[i][j][(c + 1) % 3], min); // 找到最优合并后的值minnum[i][j] = 1; //合并后,从第i堆到第j堆成为1堆cost[i][j] = Math.min(dp[i][j][0], Math.min(dp[i][j][1], dp[i][j][2])); // 合并后,从第i堆到第j堆找到最少的花费}}}}for (int k = 1; k <= n; k++) {for (int i = 1; i <= k; i++) {for (int j = k + 1; j <= n; j++) {//找到从i到j堆中,合并过后的,最少堆数,在此最少堆数的基础上再找对应的最少花费if (num[i][j] > num[i][k] + num[k + 1][j]) {num[i][j] = num[i][k] + num[k + 1][j];cost[i][j] = cost[i][k] + cost[k + 1][j];}else if (num[i][j] == num[i][k] + num[k + 1][j]) //如果堆数相同,则找到最少的花费cost[i][j] = Math.min(cost[i][j], cost[i][k] + cost[k + 1][j]);}}}System.out.println(num[1][n] + " " + cost[1][n]);}
}最大开支
题目

思路:贪心
i个人,需要花(B+K*i)*i, i + 1人则要花(B+K*(i + 1))*(i+1),多花more = B-(2*i + 1)*K块;
因此新建个类,包含K,B,i,more,再建个堆,按more从大到小排序,每次加最大的more就ok了。
import java.util.*;
import java.io.*;public class Main {static final int N = 100010;static int n, m;static PriorityQueue<item> pq = new PriorityQueue<>(new Comparator<item>() {@Overridepublic int compare(item i1, item i2) {return Integer.compare(i2.more, i1.more);}});public static void main(String[] args) throws IOException {BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));String[] str = reader.readLine().split(" ");n = Integer.parseInt(str[0]); m = Integer.parseInt(str[1]);for(int i = 0; i < m; i++) {str = reader.readLine().split(" ");int b = Integer.parseInt(str[0]);int k = Integer.parseInt(str[1]);if(k + b > 0) pq.add(new item(k, 1, b, k + b));}long ans = 0;while(!pq.isEmpty() && n > 0) { // 最多只能加n次item i = pq.poll();ans += i.more;i.more = i.k + (2 * i.times + 1) * i.b;if(i.more > 0) pq.add(new item(i.k, i.times + 1, i.b, i.more));n--;}System.out.println(ans);}static class item {int k, times, b, more;item(int k, int times, int b, int more) {this.k = k;this.times = times;this.b = b;this.more = more;}}
}魔法阵
题目

思路:dijkstra+dp
这道题如果没有魔法减伤就是一道非常标准的dijkstra算法题,加入减伤后,我们可以用dp来记录。
dp[i][j]表示的是到达第i点并且消除了连续j段的伤害。
我们可以列出状态计算公式(i是t的下一个点):
1.dp[i][0] = dp[t][0]+w[i, t]; (正常dijkstra) 2.dp[i][k] = min(dp[t][k-1],dp[i][k])
3.dp[i][K] = min(dp[t][K] + g[i][t],dp[i][K])
M是N^2级的,因此采用邻接矩阵来存路线。本来朴素dijkstra是用bool类型来储存点是否经过,但是本题有可能会重复走某一个点,所以用队列来存改变距离的点。
import java.util.*;
import java.io.*;public class Main {static final int N = 1010;static int n, m, k;static int[][] dp = new int[N][N], g = new int[N][N];static void dijkstra() {for(int i = 0; i < N; i++)for(int j = 0; j < N; j++)dp[i][j] = 0x3f3f3f3f;dp[0][0] = 0;Queue<Integer> q = new LinkedList<>();q.add(0);while (!q.isEmpty()) {int t = q.poll();for (int i = 0; i < n; i++) {if(g[t][i] < 0x3f3f3f3f) {boolean flag = false;if (dp[i][0] > dp[t][0] + g[i][t]) {dp[i][0] = dp[t][0] + g[i][t];flag = true;}for (int k1 = 1; k1 <= k; k1++) {if (dp[i][k1] > dp[t][k1 - 1]) {dp[i][k1] = dp[t][k1 - 1];flag = true;}}if (dp[i][k] > dp[t][k] + g[i][t]) {flag = true;dp[i][k] = dp[t][k] + g[i][t];}if (flag) q.add(i);}}}}public static void main(String[] args) throws IOException {BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));String[] str = reader.readLine().split(" ");n = Integer.parseInt(str[0]);k = Integer.parseInt(str[1]);m = Integer.parseInt(str[2]);for(int i = 0; i < N; i++)for(int j = 0; j < N; j++)g[i][j] = 0x3f3f3f3f;for (int i = 0; i < m; i ++ ) {str = reader.readLine().split(" ");int a = Integer.parseInt(str[0]);int b = Integer.parseInt(str[1]);int w = Integer.parseInt(str[2]);g[a][b] = Math.min(w, g[a][b]); g[b][a] = g[a][b];}dijkstra();System.out.println(Math.min(dp[n - 1][0], dp[n - 1][k]));}
}阶乘求和
题目

思路
找末尾0的数量,i>40时,i!末尾一定大于9个0(i!中乘了9个以上的5和2),由此暴力即可
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {static final int MOD = (int)1e9;public static void main(String[] args) {long ans = 0;long p = 1;for(int i = 1; i <= 40; i++){ans = (ans + p) % MOD;p = p * (i + 1) % MOD;}System.out.println(ans);}
}相关文章:

第十四届蓝桥杯大赛软件赛省赛Java大学B组
最近正在备考蓝桥杯,报的java b组,顺便更一下蓝桥的 幸运数字 题目 思路:填空题,暴力即可 import java.util.Scanner; // 1:无需package // 2: 类名必须Main, 不可修改public class Main {static int trans(int x, int y){int …...
Java二阶知识点总结(七)SVN和Git
SVN 1、SVN和Git的区别 SVN是集中式的,也就是会有一个服务器保存所有代码,拉取代码的时候只能从这个服务器上拉取;Git是分布式的,也就是说每个人都保存有所有代码,如果要获取代码,可以从其他人手上获取SV…...

Java后端八股------设计模式
Coffee可以设计成接口。...
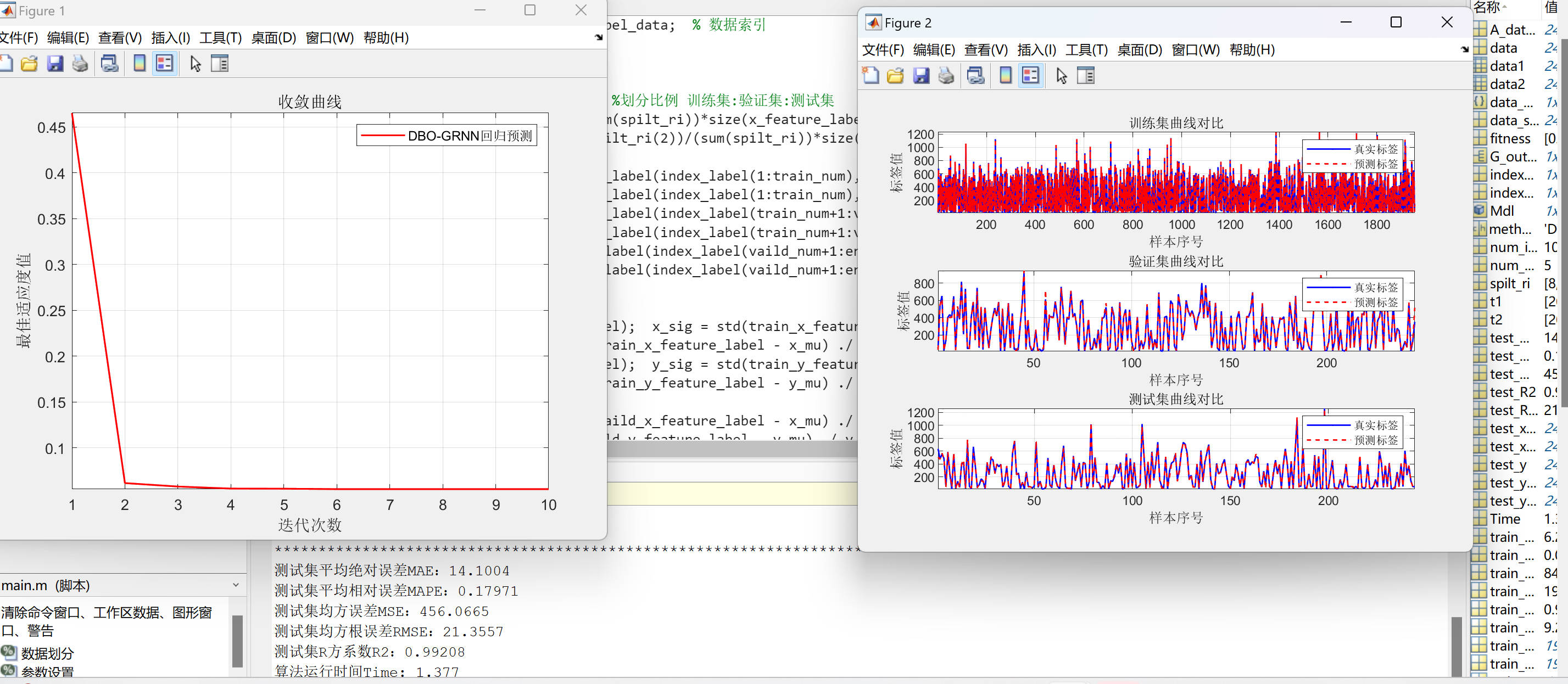
DBO优化GRNN回归预测(matlab代码)
DBO-GRNN回归预测matlab代码 蜣螂优化算法(Dung Beetle Optimizer, DBO)是一种新型的群智能优化算法,在2022年底提出,主要是受蜣螂的的滚球、跳舞、觅食、偷窃和繁殖行为的启发。 数据为Excel股票预测数据。 数据集划分为训练集、验证集、测试集,比例…...

Day 31 贪心01
理论基础 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。最好用的策略就是举反例,如果想不到反例,那么就试一试贪心吧。 贪心算法一般分为如下四步: 将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优…...

C++11特性:std::lock_guard是否会引起死锁?
今天在评审代码的时候,因为位于两个不同的线程中(一个是周期性事件线程,一个是触发式事件线程),需要对一个资源类的某些属性进行互斥的访问,因此采用lock_guard互斥量包装器,但是在升级的过程中…...
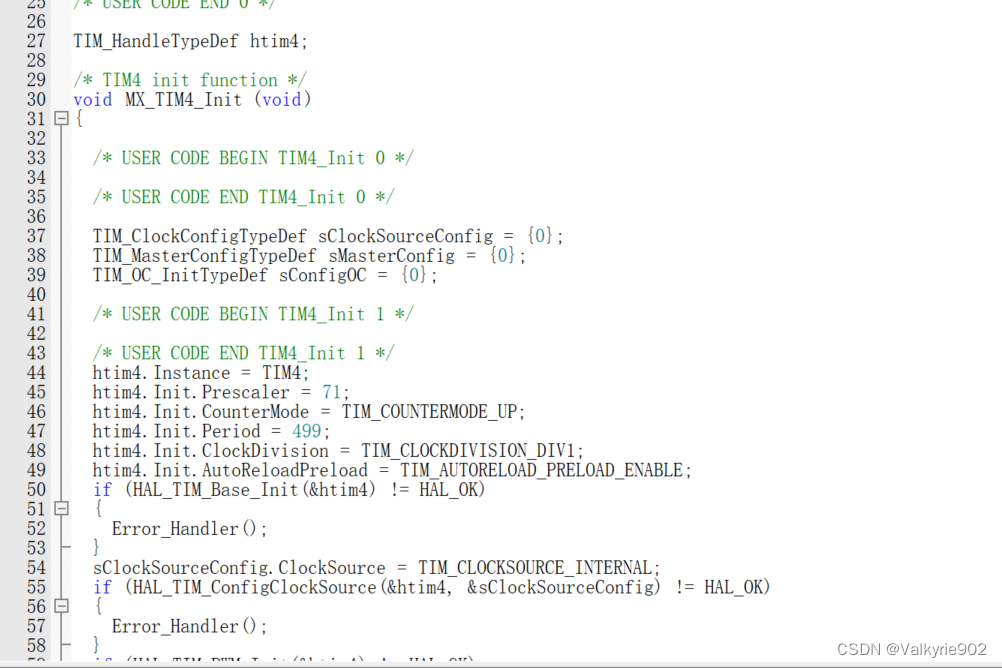
stm32使用定时器实现PWM与呼吸灯
PWM介绍 STM32F103C8T6 PWM 资源: 高级定时器( TIM1 ): 7 路 通用定时器( TIM2~TIM4 ):各 4 路 例如定时器2 PWM 输出模式: PWM 模式 1 :在 向上计数 时࿰…...

MAC本安装telnet
Linux运维工具-ywtool 目录 1.打开终端1.先安装brew命令2.写入环境变量4.安装telnet 1.打开终端 访达 - 应用程序(左侧) - 实用工具(右侧) - 终端 #注意:登入终端用普通用户,不要用MAC的root用户1.先安装brew命令 /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/H…...

[AIGC] 使用Spring Boot进行单元测试:一份指南
在现代软件开发过程中,确认你的应用正确运行是至关重要的一步。Spring Boot提供了一组实用工具和注解来辅助你在测试你的应用时,使得这个过程变得简单。下面就来分享一下如何在Spring Boot中进行单元测试。 文章目录 为什么需要单元测试Spring Boot单元测…...

使用 Go 语言统计 0-200000 的数字中,哪些是素数?
题目 使用 Go 语言统计 0-200000的数字中,哪些是素数? 思路 两种方法: 单循环遍历 1-200000 数字,并判断是否是素数。 使用了 Goroutine 和通道实现并发: 通过创建两个通道 intChan 和 primeChan,以及一…...

Fabric Measurement
Fabric Measurement 布料测量...

wayland(xdg_wm_base) + egl + opengles 使用 Assimp 加载材质文件Mtl 中的纹理图片最简实例(十六)
文章目录 前言一、3d 立方体 model 属性相关文件1. cube.obj2. cube.Mtl3. 纹理图片 cordeBouee4.jpg二、代码实例1. 依赖库和头文件1.1 assimp1.2 stb_image.h2. egl_wayland_obj_cube.cpp3. Matrix.h 和 Matrix.cpp4. xdg-shell-client-protocol.h 和 xdg-shell-protocol.c5.…...

面试常问:为什么 Vite 速度比 Webpack 快?
前言 最近作者在学习 webpack 相关的知识,之前一直对这个问题不是特别了解,甚至讲不出个123....,这个问题在面试中也是常见的,作者在学习的过程当中总结了以下几点,在这里分享给大家看一下,当然最重要的是…...
React腳手架已經創建好了,想使用Vite作為開發依賴
使用Vite作為開發依賴 安裝VITE配置VITE配置文件簡單的VITE配置項更改package.json中的scripts在根目錄中添加index.html現在可以瀏覽你的頁面了 安裝VITE 首先,在現有的React項目中安裝VITE npm install vite --save-dev || yarn add vite --dev配置VITE配置文件 …...
)
数据结构——双向链表(C语言版)
上一章:数据结构——单向链表(C语言版)-CSDN博客 目录 什么是双向链表? 双向链表的节点结构 双向链表的基本操作 完整的双向链表示例 总结 什么是双向链表? 双向链表是一种常见的数据结构,它由一系列节…...

缓存雪崩、缓存穿透、缓存预热、缓存更新、缓存降级等问题
一、缓存雪崩 简单理解:由于原有缓存失效,新缓存未到期间 (例如:设置缓存时采用了相同的过期时间,在同一时刻出现大面积的缓存过期),所有原本应该访问缓存的请求都去查询数据库了,而对数据库CPU和内存造成…...

深度学习pytorch——多层感知机反向传播(持续更新)
在讲解多层感知机反向传播之前,先来回顾一下多输出感知机的问题,下图是一个多输出感知机模型: 课时44 反向传播算法-1_哔哩哔哩_bilibili 根据上一次的分析深度学习pytorch——感知机(Perceptron)(持续更新…...
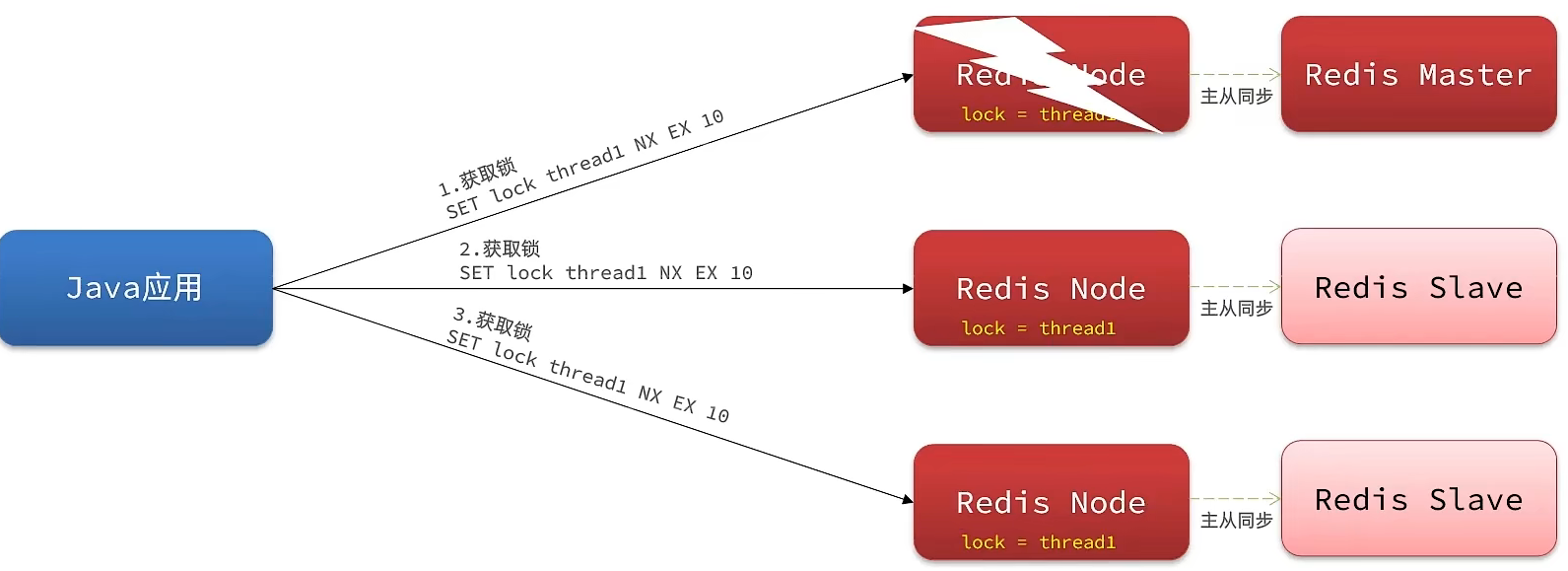
五、分布式锁-redission
源码仓库地址:gitgitee.com:chuangchuang-liu/hm-dingping.git 1、redission介绍 目前基于redis的setnx特性实现的自定义分布式锁仍存在的问题: 问题描述重入问题同一个线程无法多次获取统一把锁。当方法A成功获取锁后,调用方法B࿰…...

ARM的三个按键实验
main.c #include "key_inc.h"//封装延时函数void delay(int ms){int i,j;for(i0;i<ms;i){for(j0;j<2000;j){}}}int main(){//按键中断初始化key1_it_config();key2_it_config();key3_it_config();while(1){printf("in main pro\n");delay(1000);}re…...

高架学习笔记之需求工程
目录 一、什么是软件需求 二、需求工程 2.1. 需求获取 2.2. 需求分析 2.3. 形成需求规格 2.4. 需求确认 2.5. 需求管理 2.5.1. 变更控制 2.5.2. 版本控制 2.5.3. 需求跟踪 2.5.4. 需求状态跟踪 一、什么是软件需求 软件需求目前没有统一的定义,一般是指用…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
