算法打卡day23|回溯法篇03|Leetcode 39. 组合总和、40.组合总和II、131.分割回文串
算法题
Leetcode 39. 组合总和
题目链接:39. 组合总和
大佬视频讲解:组合总和视频讲解
个人思路
这道组合题主要是有总和的限制,当递归和超过了总和就return,递归时加上回溯去遍历数组。
解法
回溯法
把组合问题抽象为如下树形结构

如上图,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回
回溯法三部曲
1.递归函数参数
定义两个全局变量,二维数组result存放结果集,数组path存放符合条件的结果。
首先是题目中给出的参数,集合candidates, 和目标值target。
此外还需要定义int型的sum变量来统计单一结果path里的总和,startIndex来控制for循环的起始位置.
关于startIndex的使用:如果是一个集合来求组合的话,就需要startIndex,比如组合三。如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例子:Leetcode 77.组合
2.递归终止条件
终止只有两种情况,sum大于target和sum等于target。sum等于target的时候,需要收集结果
3.单层搜索的逻辑
单层for循环依然是从startIndex开始,搜索candidates集合。
本题元素为可重复选取的。所以在递归时,i不需要加1。
剪枝
这道题的剪枝就是对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。
class Solution {public List<List<Integer>> combinationSum(int[] candidates, int target) {List<List<Integer>> res = new ArrayList<>();Arrays.sort(candidates); // 先进行排序backtracking(res, new ArrayList<>(), candidates, target, 0, 0);return res;}public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {// 找到了数字和为 target 的组合if (sum == target) {res.add(new ArrayList<>(path));return;}for (int i = idx; i < candidates.length; i++) {// 如果 sum + candidates[i] > target 就终止遍历if (sum + candidates[i] > target) break;//剪枝path.add(candidates[i]);backtracking(res, path, candidates, target, sum + candidates[i], i);path.remove(path.size() - 1); // 回溯,移除路径 path 最后一个元素}}
}时间复杂度:O(n * 2^n));(循环n个元素,2^n表示所有可能的子集数量)
空间复杂度:O(n);(递归栈的深度最多为 n)
Leetcode 40.组合总和II
题目链接:40.组合总和II
大佬视频讲解:组合总和II视频讲解
个人思路
这道题的集合(数组candidates)有重复元素,但还不能有重复的组合,这是这道题难的关键,思路就是 用一个标记数组标记该元素层次上是否使用过,使用过的就跳过,这样不会出现重复的组合。
解法
回溯法
把组合问题抽象为如下树形结构:

“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上使用过,一个维度是同一树层上使用过。
元素在同一个组合内是可以重复的,怎么重复都没事,但两个组合不能相同。所以要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重。(强调:树层去重的话,需要对数组排序!)
回溯法三部曲
1.递归函数参数
除开存放数组的集合和符合条件的路径, 这道题需要加一个bool型数组used,用来记录同一树枝上的元素是否使用过。这个集合去重的重任就是used来完成的。
2.递归终止条件
终止条件为 sum > target 和 sum == target。
其中sum > target 这个条件可以省略,因为在递归单层遍历的时候,会有剪枝的操作.
3.单层搜索的逻辑
如抽线的树形结构,要去重的是“同一树层上的使用过”,判断逻辑如下:
如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。此时for循环里就应该做continue的操作。
所以值为 used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
used[i - 1] == false,说明同一树层candidates[i - 1]使用过
因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上
剪枝
当和大于目标值直接返回,即sum + candidates[i] <= target为剪枝操作
class Solution {LinkedList<Integer> path = new LinkedList<>();List<List<Integer>> ans = new ArrayList<>();boolean[] used;int sum = 0;public List<List<Integer>> combinationSum2(int[] candidates, int target) {used = new boolean[candidates.length];// 加标志数组,用来辅助判断同层节点是否已经遍历Arrays.fill(used, false);// 为了将重复的数字都放到一起,所以先进行排序Arrays.sort(candidates);backTracking(candidates, target, 0);return ans;}private void backTracking(int[] candidates, int target, int startIndex) {if (sum == target) {ans.add(new ArrayList(path));}for (int i = startIndex; i < candidates.length; i++) {if (sum + candidates[i] > target) {break;}// 出现重复节点,同层的第一个节点已经被访问过,所以直接跳过if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {continue;}used[i] = true;sum += candidates[i];path.add(candidates[i]);// 每个节点仅能选择一次,所以从下一位开始backTracking(candidates, target, i + 1);used[i] = false;sum -= candidates[i];path.removeLast();}}
}
时间复杂度:O(n * 2^n));(循环n个元素,2^n表示所有可能的子集数量)
空间复杂度:O(n);(递归栈的深度最多为 n)
Leetcode 131.分割回文串
题目链接:131.分割回文串
大佬视频讲解:分割回文串视频讲解
个人思路
既要判断是否为回文子串,还要切割,只能用回溯法了,但不知道如何切割,这是个问题...
解法
回溯法
把分割问题抽象为如下树形结构

其实本题的切割问题类似组合问题。
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个.....
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段.....
回溯法三部曲
1.递归函数参数
全局变量数组path存放切割后回文的子串,二维数组result存放结果集。
本题递归函数参数还需要startIndex,因为切割过的地方,不能重复切割
2.递归函数终止条件
按照切割的思想去看,切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
那么在代码里什么是切割线呢?其实在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
3.单层搜索的逻辑
在
for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。首先判断这个子串是不是回文,如果是回文,就加入
path中,path用来记录切割过的回文子串。注意切割过的位置,不能重复切割,所以,backtracking(s, i + 1); 传入下一层的起始位置为i + 1。
判断回文子串
可以使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。
这里需要一个个判断
class Solution {List<List<String>> result= new ArrayList<>();//结果集Deque<String> path = new LinkedList<>();public List<List<String>> partition(String s) {backTracking(s, 0);return result;}private void backTracking(String s, int startIndex) {//如果起始位置大于s的大小,说明找到了一组分割方案if (startIndex >= s.length()) {result.add(new ArrayList(path));return;}for (int i = startIndex; i < s.length(); i++) {//如果是回文子串,则记录if (isPalindrome(s, startIndex, i)) {String str = s.substring(startIndex, i + 1);path.addLast(str);} else {continue;}backTracking(s, i + 1);//起始位置后移,保证不重复path.removeLast();}}//判断是否是回文串private boolean isPalindrome(String s, int startIndex, int end) {for (int i = startIndex, j = end; i < j; i++, j--) {if (s.charAt(i) != s.charAt(j)) {return false;}}return true;}
}时间复杂度:O(n * 2^n));(循环n个元素,2^n表示所有可能的子集数量)
空间复杂度:O(n);(递归栈的深度最多为 n)
以上是个人的思考反思与总结,若只想根据系列题刷,参考卡哥的网址代码随想录算法官网
相关文章:

算法打卡day23|回溯法篇03|Leetcode 39. 组合总和、40.组合总和II、131.分割回文串
算法题 Leetcode 39. 组合总和 题目链接:39. 组合总和 大佬视频讲解:组合总和视频讲解 个人思路 这道组合题主要是有总和的限制,当递归和超过了总和就return,递归时加上回溯去遍历数组。 解法 回溯法 把组合问题抽象为如下树形结构 如上…...
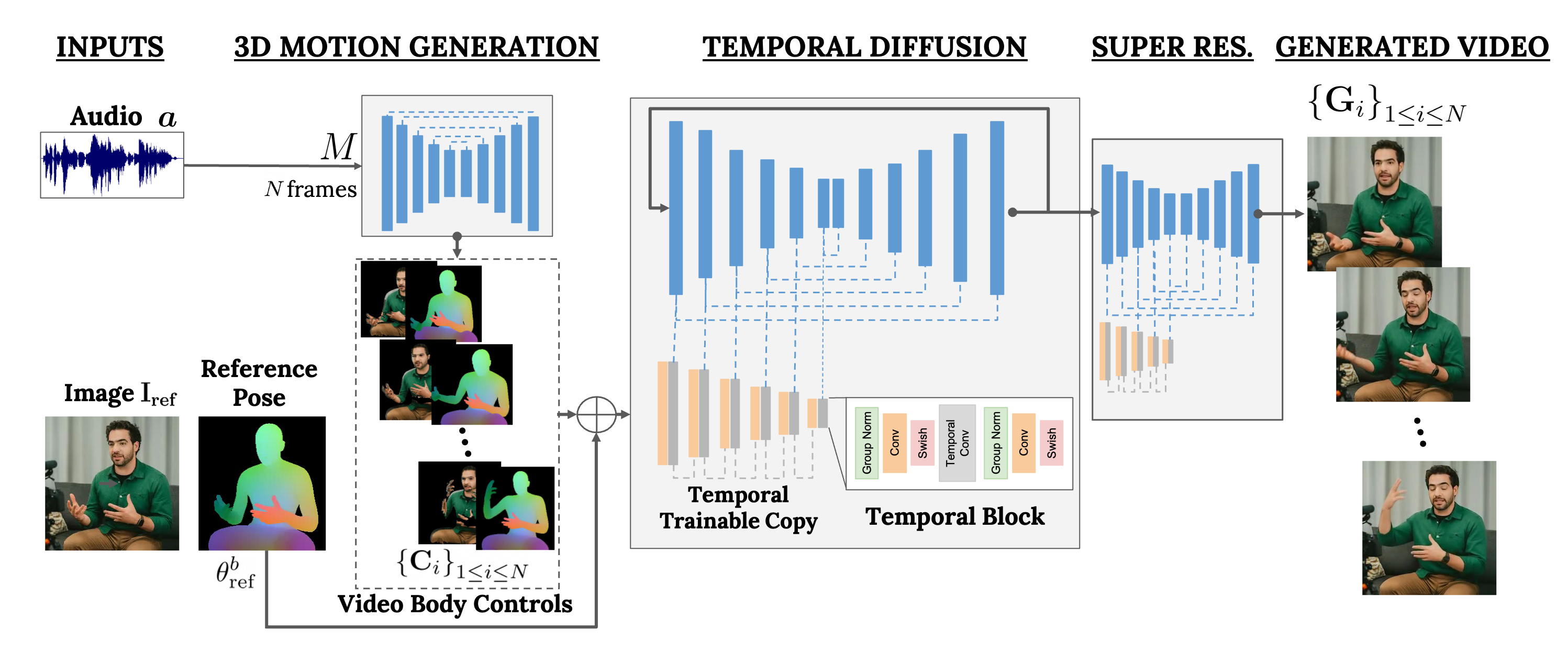
Google研究者们提出了VLOGGER模型
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

Python从入门到精通秘籍十九
一、Python之union 联合类型注释 当谈论Python中的联合类型注释时,通常会提到Union类型。Union是typing模块中定义的一个泛型类,用于表示多个可能的类型。 Union的语法如下: Union[type1, type2, ...]其中type1, type2, … 是要组成联合类…...
解决:您还有0天的时间继续使用internet download manager
通过修改注册表来白嫖的IDM方法 1、新建txt文件复制代码(命名为idm.reg) 2、代码如下 Windows Registry Editor Version 5.00[-HKEY_CURRENT_USER\Software\Classes\CLSID\{7B8E9164-324D-4A2E-A46D-0165FB2000EC}] [-HKEY_CURRENT_USER\Software\Clas…...

操作系统目录
北航操作系统 chapter 1 北航操作系统 chapter3-1 内存管理 北航操作系统chapter3-2 内存管理 北航操作系统chapter3-3 页式管理 北航操作系统chapter3-4 段式管理 北航操作系统chapter3-5 虚拟内存管理 操作系统chapter4-1 进程与线程 北航操作系统-chapter4.2 同步与互斥…...

常用的Node.js命令集锦
当使用Node.js开发时,以下是一些常用的Node.js命令集锦: npm init 用于初始化一个新的Node.js项目,并创建一个package.json文件来管理项目的依赖和元数据。 npm install [package-name] 用于安装指定的Node.js包,可以通过--save选…...
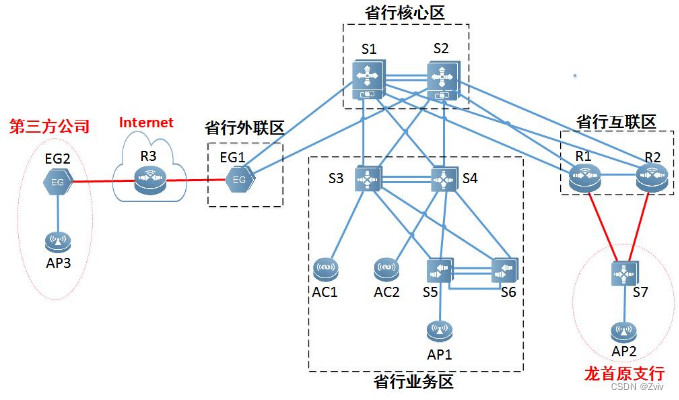
2021年XX省赛职业院校技能大赛”高职组 计算机网络应用赛项 网络构建模块竞赛真题
“2021年XX省赛职业院校技能大赛”高职组 计算机网络应用赛项 网络构建模块竞赛真题 目录 一.考试说明 1 二.模块B网络构建 2 (一)任务描述 2 (二)任务清单 9 一.考试说明 本模块比赛时间为…...

80386 ATT汇编语法
文章目录 gcc的预处理,不进行编译、汇编或链接预处理编译汇编 8.8.2 AT&T语法与英特尔语法8.8.3操作码命名8.8.4寄存器命名8.8.5操作码前缀8.8.6内存引用8.8.7跳转指令的处理8.8.8浮点8.8.9写入16位代码8.8.10笔记 gcc的预处理,不进行编译、汇编或链…...
如何在Linux系统使用宝塔面板搭建Inis博客并发布至公网【内网穿透】
文章目录 前言1. Inis博客网站搭建1.1. Inis博客网站下载和安装1.2 Inis博客网站测试1.3 cpolar的安装和注册 2. 本地网页发布2.1 Cpolar临时数据隧道2.2 Cpolar稳定隧道(云端设置)2.3.Cpolar稳定隧道(本地设置) 3. 公网访问测试总…...
【漏洞复现】netgear路由器 boarddataww 存在RCE漏洞
免责声明:文章来源互联网收集整理,请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该…...

什么是原型链
1、原型链的本质 是一个链表,当使用一个构造函数时,就会返回一个实例,在这个实例上找某个属性未找到时,则会顺着proto属性指向它的原型,去原型上找,如果原型也没有的话,则会顺着原型的原型找&a…...

什么是虚拟线程?
1、典型回答 Java 中的虚拟线程,也叫做协程或“轻量级线程”,它诞生于JDK 19(预览 API),正式发布于 JDK 21,它是一种在 Java 虚拟机(JVM)层面实现的逻辑线程,不直接和操作系统的物理线程一一对应,因此它可…...

node.js是什么怎么用常用方法
什么是node.js Node.js是一个基于Chrome V8 JavaScript引擎的服务器端运行环境。它允许使用JavaScript来开发高性能的网络应用程序。Node.js采用事件驱动、非阻塞式I/O模型,使其能够处理大量并发请求而不会出现阻塞。 Node.js最初是由Ryan Dahl于2009年创建的&…...
pikachu靶场第十四关——XSS(跨站脚本)之js输出(附代码审计)
源代码: //这里讲输入动态的生成到了js中,形成xss //javascript里面是不会对tag和字符实体进行解释的,所以需要进行js转义//讲这个例子主要是为了让你明白,输出点在js中的xss问题,应该怎么修? //这里如果进行html的实体编码,虽然可以解决XSS的问题,但是实体编码后…...

AD实用设置教程
目录 一、“多边形敷铜” 设置 “最小间隔” 二、放置的 “过孔” 敷铜 “全连接”...

webpack为什么要使用loader,如何手写loader
webpack是一个打包工具,即webpack会将一切文件视为模块,但是webpack在打包的时候只是认识JS文件或者JSON文件,并不认识CSS文件,png图片等,如果想让webpack能够在打包的时候识别其他文件,就必须要使用loader…...

【银河商学】大蓝短视频学习04——找对标账号
为什么要找对标账号? 标准答案,少走弯路秒上热搜,快速起号预知变现,扬长避短 找什么样的对标账号? 成熟 粉丝量 > 50万持续更新,多年屹立不倒 举例账号 三百者也 模仿 二百者也 易做 简单可量产 有潜…...

Java练手游戏--俄罗斯方块
Java基础小练手游戏项目:俄罗斯方块简单版 使用Java实现俄罗斯方块大概思路: 界面设计: 使用Java Swing或JavaFX创建游戏窗口和用户界面。创建一个主窗口类(如GameFrame.java),负责设置窗口大小、标题等属…...
基础篇Redis
基础篇Redis 1.Redis简单介绍 Redis是一种键值型的NoSql数据库,这里有两个关键字: 键值型NoSql 其中键值型,是指Redis中存储的数据都是以key.value对的形式存储,而value的形式多种多样,可以是字符串.数值.甚至json…...

透视变换详解
透视变换(Perspective Transformation)是一种用于在图像处理中对图像进行几何变换的技术,它可以用来校正图像的透视形变或者改变图像的视角。透视变换通常涉及到一个原始图像和一个目标图像之间的转换,其中原始图像可能是一个投影…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...
