学习次模函数-第1章 引言
许多组合优化问题可以被转换为集合函数的最小化,集合函数是在给定基集合的子集的集合上定义的函数。同样地,它们可以被定义为超立方体的顶点上的函数,即
,其中
是基集合
的基数-它们通常被称为伪布尔函数[27]。在这些集合函数中,次模函数起着重要的作用,类似于向量空间上的凸函数,因为在实际问题中出现的许多函数都是次模函数或其轻微的修改的,在计算机科学和应用数学的许多领域中有应用,例如机器学习[125,157,117,124],计算机视觉[31,96],运筹学[98,182],电气网络[162]或经济学[203]。由于次模函数可以精确最小化,并且在某些保证下近似地最大化,因此在多项式时间内,它们很容易为它们所应用的所有众多问题带来有效的算法。它们也出现在理论计算机的几个领域中科学,如拟阵理论[189]。
然而,对次模函数的兴趣并不限于离散优化问题。 事实上,次模函数的丰富结构及其通过Lovász扩展与凸分析的联系[135]和各种相关的多面体使它们特别适用于组合优化之外的问题,即作为信号处理和机器学习问题中的正则化器[38,7]。
实际上,许多连续优化问题表现出潜在的离散结构(例如, 基于链、树或更一般的图)和次模函数提供了有效和通用的工具来捕获这样的组合结构。
在这本专著中,次模函数的理论以一种独立的方式呈现,所有结果都是从机器学习中常见的凸分析的第一原理证明的,而不是依赖于组合优化和传统的理论计算机科学概念,如拟阵或流(见,例如, [72]有关这些方法的参考书)。 此外,我们提出的算法是基于传统的凸优化算法,如单纯形法线性规划,二次规划的有效集方法,椭球方法,切割平面,和条件梯度。 这些将详细介绍,特别是在次模函数最小化及其各种连续扩展的背景下。 假设具有良好的凸分析知识(见,例如, [30,28]),并在附录A中对重要概念进行了简短的回顾-更多详细信息,请见,例如, [95,第30、28、185页]。
各章大纲。分为几个章节,总结如下(在目录中,第一次阅读时可以跳过的章节用星星标记):
(1)定义:在第二章中,我们给予了次模函数及其相关多面体的不同定义,特别是基多面体和次模多面体,它们在次模分析中是至关重要的,因为许多算法和模型都可以用这些多面体自然地表示。
(2)Lovász扩展:在第三章中,我们将Lovász扩展定义为从定义在上的函数到定义在
上的函数的扩展(然后是
),并给予它的主要性质,特别是给出了次模分析中的关键结果:Lovász扩展是凸的当且仅当集函数是次模的;此外,最小化次模集函数
等价于最小化
上的Lovász扩展。这意味着次模函数最小化可以在多项式时间内解决。最后,通过所谓的“贪婪算法”建立了Lovász扩展和次模多面体之间的联系:Lovász扩展是基多面体的支撑函数,并且可以以封闭形式计算。
(3)多面体:第四章将进一步研究伴随多面体,计算线性函数的支撑函数和伴随极大化子,我们还详细讨论了这种多面体的面结构,这在第五章中与Lovász扩展的稀疏诱导性质相关时将很有用。
(4)次模罚函数的凸松弛:虽然次模函数可以直接使用(用于集函数的最小化或最大化),但我们在第5章中展示了如何使用它们来惩罚向量的支撑集或水平集,由此产生的混合组合/连续优化问题可以使用Lovász扩展自然地松弛为凸优化问题。
(5)示例如下:在第6章中,我们介绍了次模函数的经典例子,以及在机器学习中的几个应用,特别是割,集合覆盖,网络流,熵,谱函数和拟阵。
(6)非光滑凸优化:在第七章中,我们回顾了经典的迭代算法,如次梯度法、椭球法、单纯法、割平面法、有效集法和条件梯度法,并特别注意在适用的情况下提供这些算法的原始/对偶解释。
(7)可分离优化-分析:在第八章中,我们考虑了由Lovász扩展正则化的可分优化问题,即形式为
的问题,并证明了这如何等价于一系列次模函数极小化问题。这是与次模函数相关的组合优化问题和凸优化问题之间的关键理论联系,这将在后面的章节中使用。
(8)可分离优化-算法:在第9章中,我们提出了两套可分离优化问题的算法。 第一个算法是一个精确的算法,它依赖于一个有效的次模函数最小化算法的可用性,而第二组算法是基于现有的凸优化迭代算法,其中一些来与在线和离线的理论保证。 我们考虑有效集方法(“最小范数”算法)和条件梯度方法。
(9)次模函数最小化:在第10章中,我们介绍了各种次模函数最小化的方法。 我们简要介绍了精确次模函数最小化的组合算法,并专注于更深入地使用特定的凸优化问题,可以迭代求解,以获得近似或精确解次模函数最小化,有时理论保证和近似最优性证书。 我们考虑了次梯度法,椭球法,单纯形算法和解析中心割平面。 我们还展示了第8章和第9章中的可分离优化问题如何用于次模函数最小化。 第12章将对这些方法进行实证比较。
(10)次模块优化问题:在第11章中,我们提出了其他组合优化问题,可以部分解决使用次模分析,如次模函数最大化和次模函数的差异的优化,并将这些问题与非凸优化问题的次模多面体。 虽然这些问题通常不能在多项式时间内解决,但许多算法都具有基于次模性的近似保证。
(11)实验:在第12章中,我们提供了前面描述的优化算法的例子,用于次模函数最小化,以及凸优化问题(可分或不可分)。 所有这些实验的Matlab代码可以在http://www.di.ens.fr/~fbach/submodular/上找到。
在附录A中,我们回顾了凸分析的相关概念(如Fenchel对偶、对偶范数、规范函数和极集),而在附录B中,我们给出了与次模函数相关的几个结果,如保持次模性的运算。
已经有几本关于同一主题的书籍和专著文章,本专著中提供的材料依赖于这些[72,162,126]。 然而,为了以最简单的方式呈现材料,也使用了相关研究论文的思想,并更加强调凸分析和优化。
符号。 我们考虑集合,其幂集为
,由
的
个子集组成。 给定一个向量
,
也表示定义为
的模集函数。此外,
意味着
是
的子集,可能等于
。 我们表示为
集合
的基数,并且,对于
,
表示集合
的指示向量。 若
,则
表示
定义为
,我们称之为弱(或强)
-超水平集。 类似地,如果
,我们记为
。
对于,我们用
表示
的
-范数,定义为
,其中
且
。最后,我们用
表示非负实数集,用
表示非零实数集,用
表示严格正实数集。
相关文章:
学习次模函数-第1章 引言
许多组合优化问题可以被转换为集合函数的最小化,集合函数是在给定基集合的子集的集合上定义的函数。同样地,它们可以被定义为超立方体的顶点上的函数,即,其中是基集合的基数-它们通常被称为伪布尔函数[27]。在这些集合函数中&…...

实在数字员工,助力菜鸟智慧物流高效腾飞,领航行业新高度
秉承人人都有一个智能助理的发展愿景,自2023年首个数字员工落地以来,菜鸟数字员工累计运行时长已达10万小时。 在智能物流科技不断飞速迭代的今天,物流行业作为社会经济运行的重要支柱和电子商务生态链的关键环节,面临着前所未…...

【from PIL import Image】PIL库和Image的功能及用法
from PIL import Image代码 from PIL import Image 是 Python 中导入 PIL 库中的 Image 模块。PIL 是 Python Imaging Library 的缩写,它是 Python 中用于图像处理的一个强大的库。而 Image 模块则是 PIL 库中的一个子模块,提供了处理图像的各种功能。 …...
【python从入门到精通】--第一战:安装python
🌈 个人主页:白子寰 🔥 分类专栏:python从入门到精通,魔法指针,进阶C,C语言,C语言题集,C语言实现游戏👈 希望得到您的订阅和支持~ 💡 坚持创作博文…...

MySQL的利用分区功能将数据存储到不同的磁盘
MySQL支持将不同的分区存储在不同的磁盘或目录上,这可以进一步优化I/O性能和存储利用率。具体的操作步骤如下: 首先需要确保MySQL的数据目录配置允许在不同目录存储数据文件。在MySQL配置文件(my.cnf或my.ini)中添加以下配置项: [mysqld] innodb_file_per_table1 这个配置项…...

KDB+Q | D1 | 学习资源 基础数据类型
官网会是主要的学习资源:https://code.kx.com/q/ 中文教程可能读起来会快一点: https://kdbcn.gitee.io/ 参考了还不错的学习经验帖:https://www.jianshu.com/p/488764d42627 KDB擅长处理时序数据, KDB数据库是后端数据库&…...
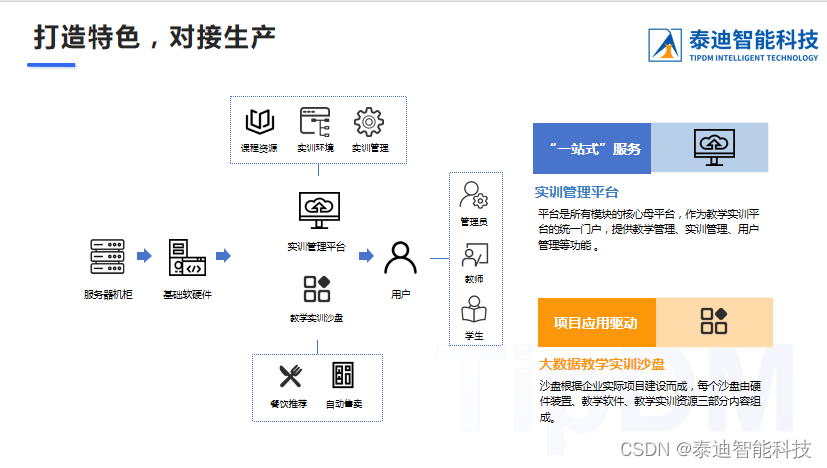
中等职业学校大数据课程建设方案
大数据产业是以数据及数据所蕴含的信息价值为核心生产要素,通过数据技术、数据产品、数据服务等形式,使数据与信息价值在各行业经济活动中得到充分释放的赋能型产业。 大数据产业定义一般分为核心业态、关联业态、衍生业态三大业态。 一、专…...

.NET 依赖注入和配置系统
文章目录 依赖注入DI几个概念.NET 中使用DI生命周期IServiceProvider的服务定位器方法 配置系统Json文件配置绑定类读取配置 依赖注入 依赖注入(Dependency Injection,DI)是控制反转(Inversion of Control,IOC…...

什么是”法兰“?
“法兰”,第一次听说这个词,怪怪的,后来就知道了和“鲁棒”是一类人才发明的词; 所以就知道这个词原本是“flange”; 那这样就好解释了, 【 使物体更加坚固或(如火车车轮)保持正确…...
Vulnhub靶机:HackLAB_Vulnix
一、介绍 运行环境:Virtualbox(攻击机)和VMware(靶机) 攻击机:kali(192.168.56.101) 靶机:HackLAB: Vulnix(192.168.56.110) 目标:获取靶机root权限和flag 靶机下载地址&#x…...

软件推荐 篇三十七:开源免费无广告的在线音乐免费播放 | MusicFree纯净无广告体验-小众冷门推荐
引言 自从QQ音乐没了杰伦、某云开始收费,除了各种广告弹窗导致电脑卡的要死,打工人就靠这点音乐背景熬夜了,木有办法,得有个开源免费的听歌软件吧,一搜github,软件一大堆,作为一个打工仔&#…...

Hive SQL必刷练习题:留存率问题(*****)
留存率: 首次登录算作当天新增,第二天也登录了算作一日留存。可以理解为,在10月1号登陆了。在10月2号也登陆了,那这个人就可以算是在1号留存 今日留存率 (今日登录且明天也登录的用户数) / 今日登录的总…...

在Linux/Ubuntu/Debian中创建自己的命令快捷方式
虽然图标快捷方式使你移动鼠标双击就打开目标,但是你还是需要先定位到它。而在终端Terminal中你只需要输入一个自定义命令就能一步到位。 要在 Ubuntu 中创建你自己的命令或别名,你可以使用主目录中的“.bashrc”文件。 以下是创建通过 Wine 运行 Photo…...

vue学习笔记——Vue3循环生成表单时,对每一行新生成的数据添加表单验证的方法
应用场景: 在form表单内,动态生成一个数组类型的一组数据,要求对生成的每一组数据内容进行表单验证。例如动态添加人员,并对每个人的人员的信息输入框进行表单验证。 解决思路: 把rules的验证规则循环写在element ui的…...

用C++做一个植物大战僵尸
制作一个完整的“植物大战僵尸”游戏是一个非常大的项目,涉及图形渲染、碰撞检测、用户输入处理、音效、动画、游戏逻辑等多个方面。由于这个话题非常广泛,我可以提供一个简化的版本或者一个框架来启动你的项目。 以下是一个简化的框架,帮助…...
政安晨:【深度学习实践】【使用 TensorFlow 和 Keras 为结构化数据构建和训练神经网络】(三)—— 随机梯度下降
政安晨的个人主页:政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: TensorFlow与Keras实战演绎 希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正! 这篇文章中,咱们将使用Keras和TensorFlow…...

普通用户无法连接到docker服务
环境 tt:~$ lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 22.04.3 LTS Release: 22.04 Codename: jammy问题 tt:~$ sudo apt install docker.io -ytt:~$ docker info Client:Version: 24.0.5Context: d…...
——Rancher部署Nginx(单机版))
Rancher(v2.6.3)——Rancher部署Nginx(单机版)
Rancher部署Nginx详细说明文档:https://gitee.com/WilliamWangmy/snail-knowledge/blob/master/Rancher/Rancher%E4%BD%BF%E7%94%A8%E6%96%87%E6%A1%A3.md#5rancher%E9%83%A8%E7%BD%B2nacos ps:如果觉得作者写的还行,能够满足您的需求&#x…...

java问题解释
问题1:请解释Java中的异常处理机制,并讨论其在软件开发中的重要性。 回答: Java中的异常处理机制是一种强制性的错误处理机制,它允许程序在运行时检测到异常情况,并采取适当的措施进行处理。异常是在程序执行过程中发…...

TSN协议原理!看完这一篇就够了(1)——时钟同步IEEE802.1AS-2020
▎前言 在许多应用场景中,一个本地局域网中互联的设备集群需要共享同一个时间,以支持各设备的协同工作。例如:音频设备与视频设备的配合播放,雷达与摄像头的数据融合等;这样一个看似简单的域功能,细化成为…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
