map和set(三)——红黑树
1、红黑树的概念及性质
1.1概念
概念:
红黑树是一种二叉搜索树,以颜色(Red or Black)互斥来限制每条路径不会比另外的路径长出两倍,来达到近似平衡
1.2性质
红黑树的性质:
- 每个节点不是黑色就是红色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子节点必须是黑色的(无连续的红节点)
- 对于每个节点,从该节点到其所有的后代叶节点的简单路径上,均包含相同数目的黑节点(每条路径都包含相同数量的黑色节点)
- 每个叶子节点都是黑色的(此叶子节点指的是NULL)
得知上面的有关红黑树的情况后,思考一个一个问题
它的性质如何保证最长路径不会超过最短路径的两倍?
考虑极端场景:
最短路径: 全黑 最长路径:一直一黑一红
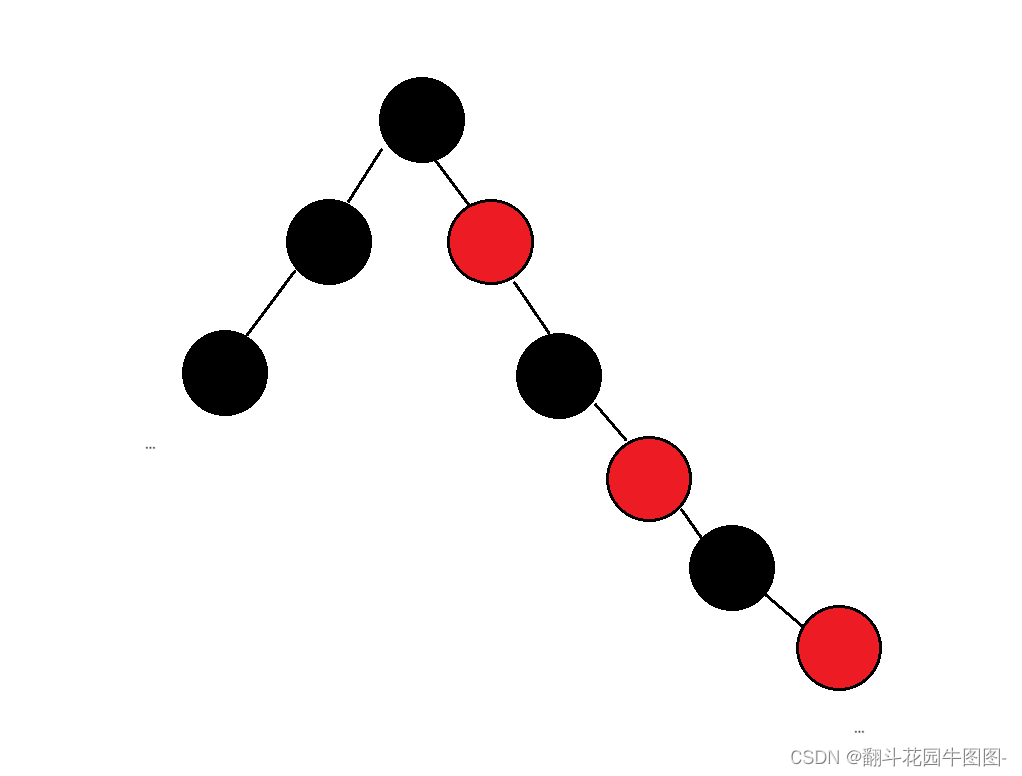
对比AVL树,高度是很接近logN
红黑树高度是很接近2*logN(红黑树搜索效率相对差一些,但几乎可以忽略不计)
但插入同样的数据,AVL树的高度更低,是通过多次旋转而得来的
2、红黑树的简单实现
2.1红黑树节点的定义
enum(枚举)里存的是节点的颜色
节点要有指向左节点、右节点、父节点的指针;节点存的值(数据)及节点的颜色
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};初始化(构造)节点,三指针指向空;_kv(值or数据)取决于传的值,_col默认为红色
为什么(插入)节点的颜色默认为红色呢?
如果插入黑色节点就会破坏规则:每条路径上黑色节点的数量相同
所以(插入)节点的默认颜色为红色
2.2插入
以下为简写:
u uncle 叔叔
p parent 父亲
g grandfather 爷爷
c cur遍历节点(可能是新插入节点)
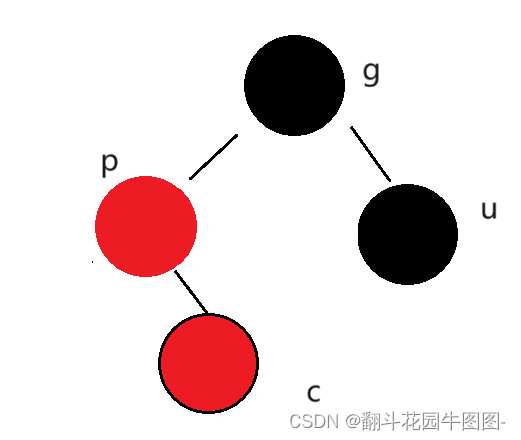
情况一:
u(叔叔)存在且为红
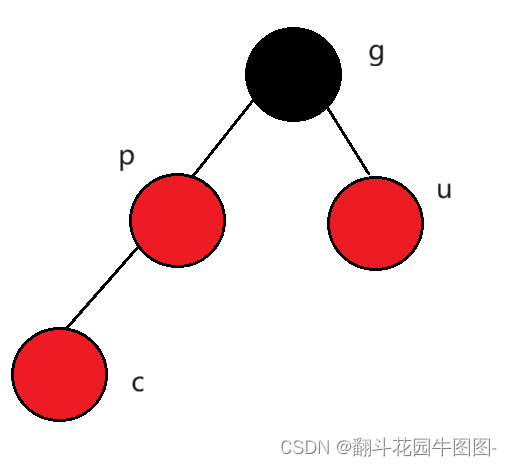
g必为黑,若为红早就违反没有连续两个红色节点的规则
此时c节点一定是新插入的节点,且c节点的插入破坏了没有连续的红色节点的规则,所以我们需要对这颗红黑树进行调整
把g的颜色改为红色,将p/u的颜色改为黑色
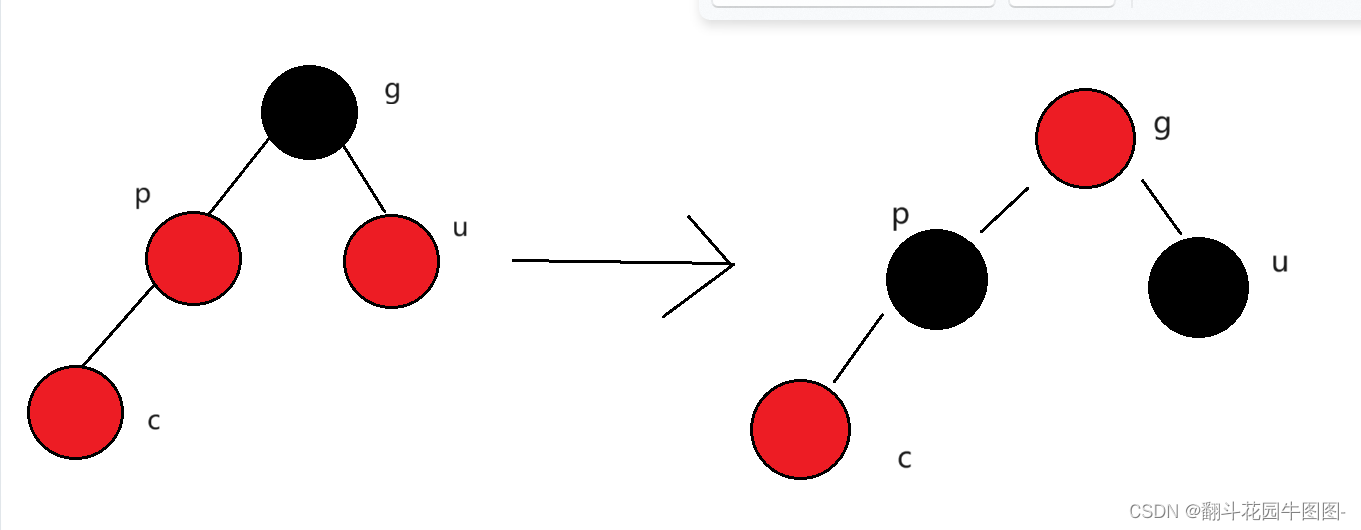
注意:
g节点可能为根节点
若g节点为根节点,那么再将g节点变黑(根节点的颜色必须为黑色),所有路径的黑色节点+1,所有路径的黑色节点数依然相等
若g节点非根节点,那么只需要将g作为cur继续向上调整颜色
情况二
叔叔不存在或叔叔存在且为黑
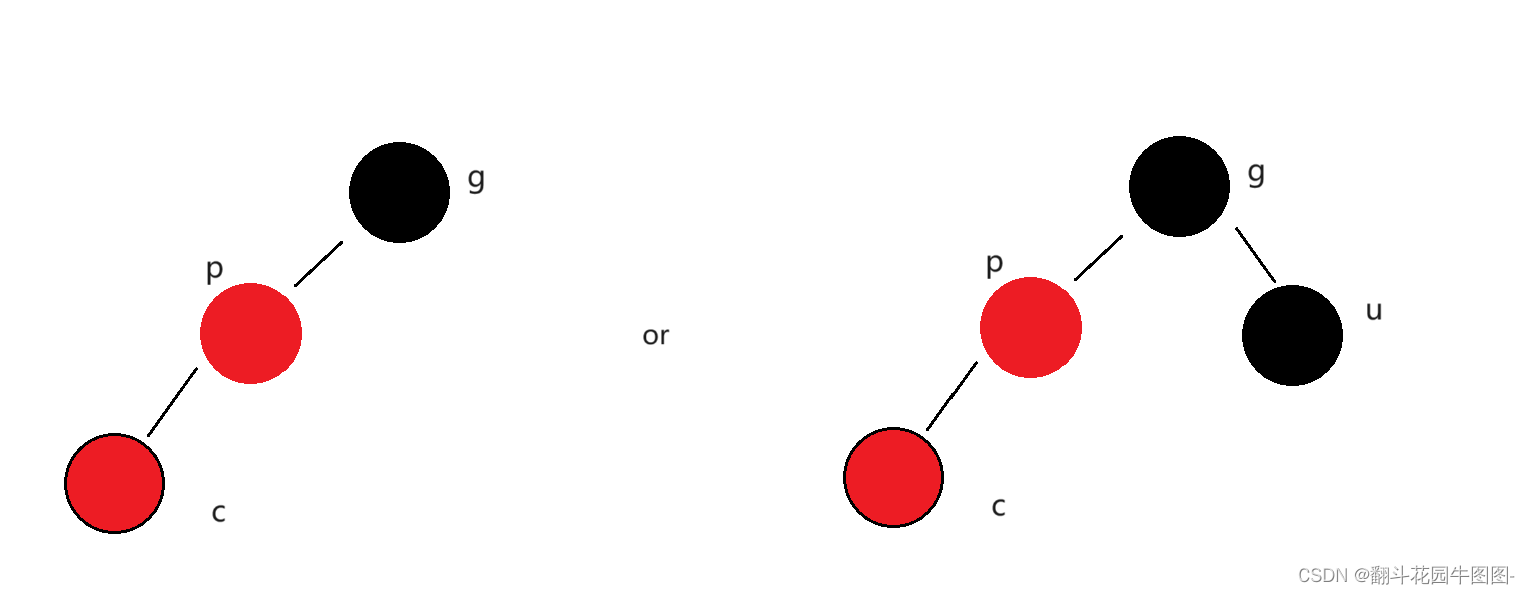
若叔叔不存在
那么c节点一定是新插入节点,因为叔叔不存在,那么p父亲下面就不能再挂黑色节点了(往p下面挂p路径有黑色节点,而u却没有),不然就会违反"所有路径的黑色节点数量都相等"这条规则
若叔叔存在且为黑
那么c节点一定不是新插入的节点,若c节点为新插入节点,则在插入c之前就会违反"所有路径黑色节点数量相同"这一规则(g和u都为黑而p却非黑,c为插入默认为红,不平衡了);c不是新插入节点那么c节点下面一定有黑色节点对应黑色的u节点以达到平衡
这时候我们就要用到之前AVL数所用的旋转了
叔叔不存在
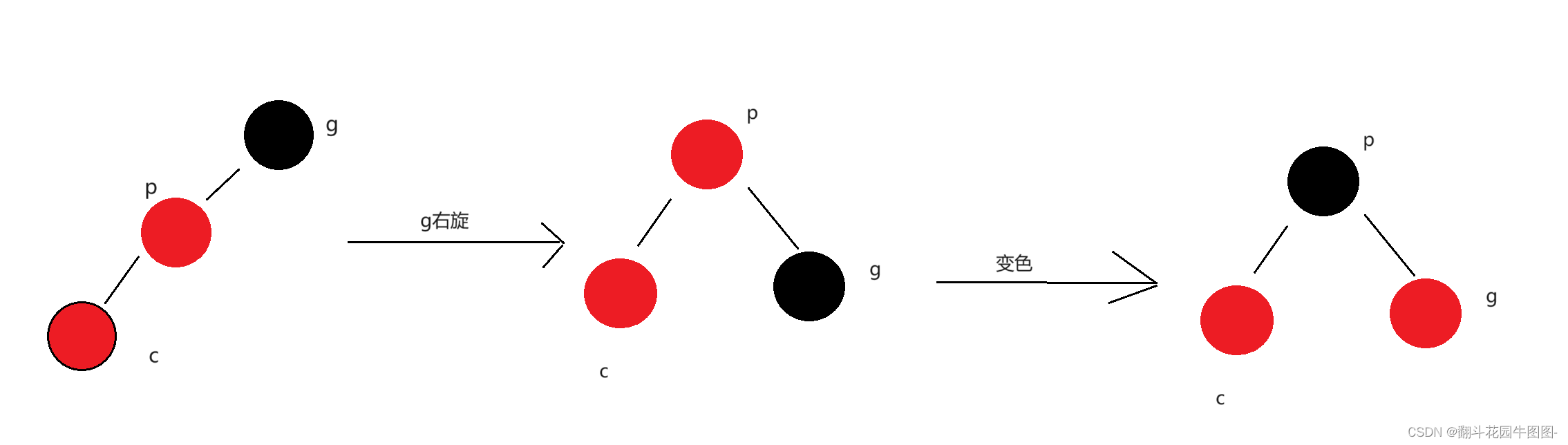
叔叔存在且为黑
对g进行右旋(p为g的左、c为p的左),然后将p改为黑色,g改为红色
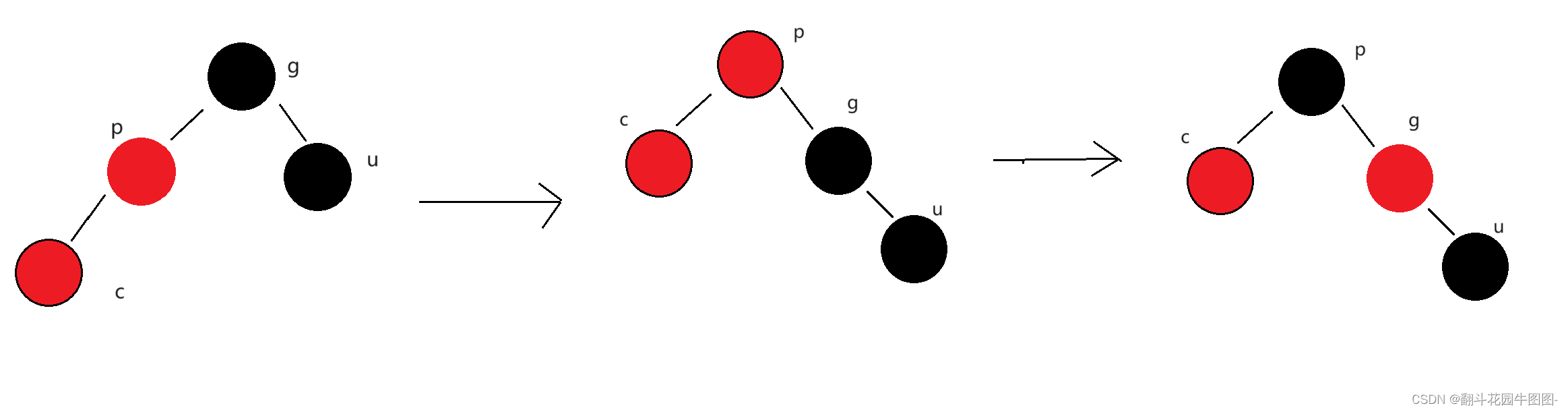
上面的情况都是基于c节点在p节点左子树(左孩子节点)的条件下
当cur在p节点的右边,情况又是怎样的呢?
叔叔不存在
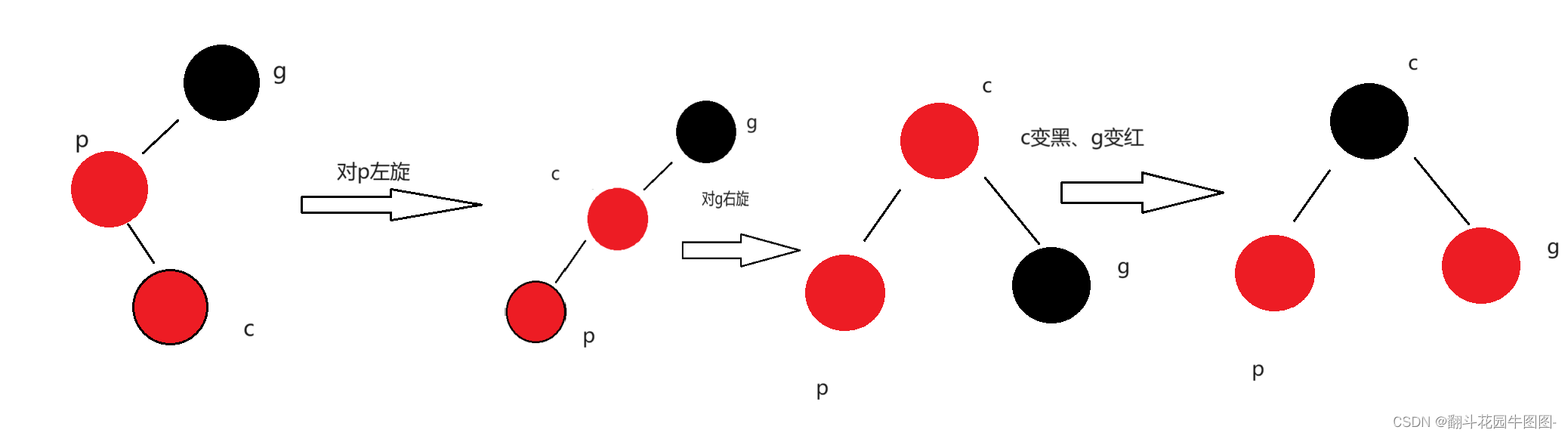
叔叔存在且为黑
当p为g的左而c为p的右边,单纯的单选已经解决不了了
要先对p进行左单旋,在对g进行右单旋(对比上下两个图就知道,其实只多了一步)
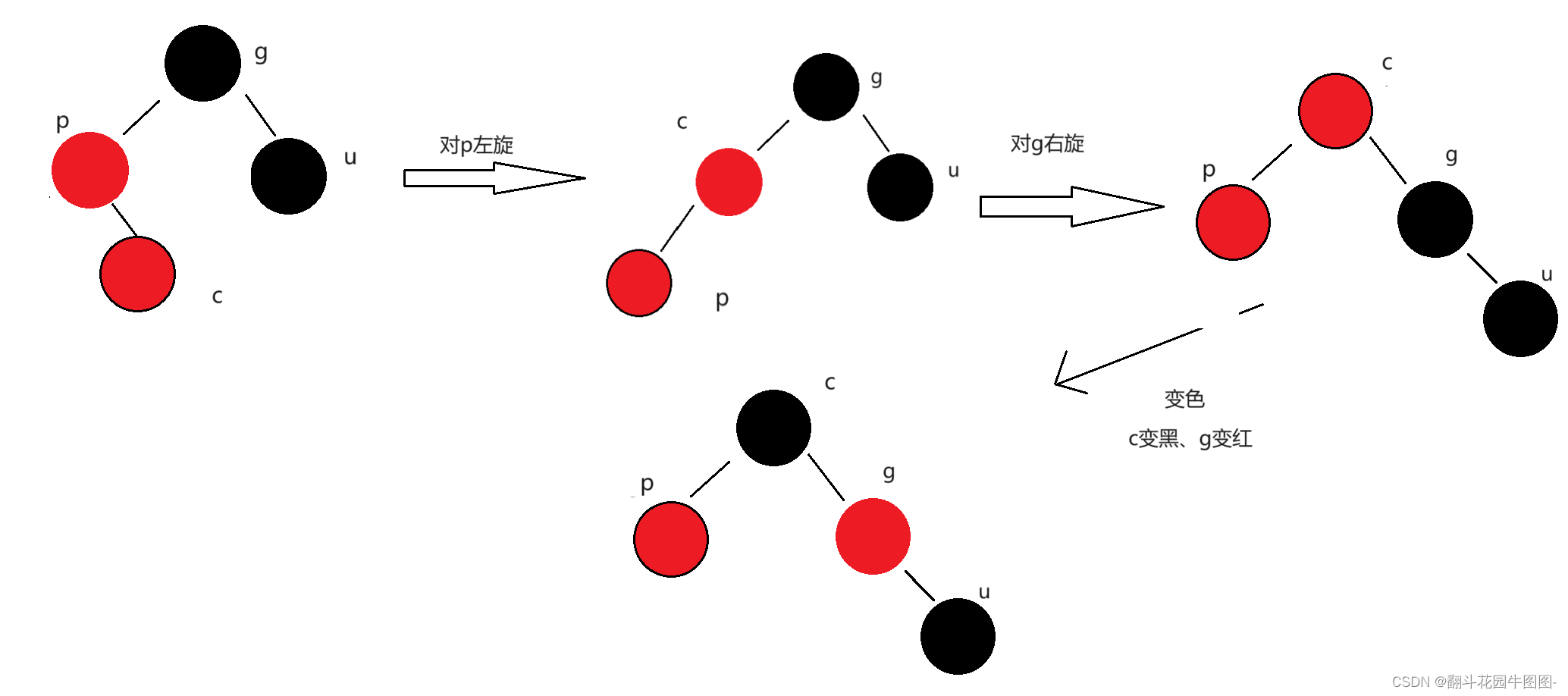
以上的所有情况都是基于父亲在爷爷左边的基础上的,还有父亲在爷爷右边的几种情况,不过和上面的大差不差,我就不细讲了
红黑树其本质还是二叉搜索树,红黑树的插入还是以二叉搜索树的插入为基础所更改的
大概可以分为两步:
1. 以二叉搜索树的方式插入新节点
2. 检测新节点插入后,红黑树的性质是否造到破坏(对其进行旋转或变色)
代码
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr)//如果根节点为空,开新节点,将根节点的颜色改为黑,返回真{_root = new Node(kv);_root->_col = BLACK;return true;}//二叉搜索树方式遍历Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//走到这说明已经找到可以插入的地方 //创建一个新节点cur = new Node(kv); // 红色的//判断插入的节点该连接到父节点的左还是右if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//检测新节点插入后,红黑树的性质是否造到破坏while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left)//父亲在爷爷左{Node* uncle = grandfather->_right;// 情况一:叔叔存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else{// 情况二:叔叔不存在或者存在且为黑// 旋转+变色if (cur == parent->_left){RotateR(grandfather); // gparent->_col = BLACK; // p ugrandfather->_col = RED; // c}else{RotateL(parent);RotateR(grandfather); // gcur->_col = BLACK; // p ugrandfather->_col = RED; // c}break;}}else//父亲在爷爷右边{Node* uncle = grandfather->_left;// 情况一:叔叔存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{// 情况二:叔叔不存在或者存在且为黑if (cur == parent->_right){RotateL(grandfather); // gparent->_col = BLACK; // u pgrandfather->_col = RED; // c}else{RotateR(parent);RotateL(grandfather); // gcur->_col = BLACK; // u pgrandfather->_col = RED; // c}break;}}}_root->_col = BLACK;return true;
}左旋右旋的代码
void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}
2.3红黑树的验证
红黑树的检测分为两步:
1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
2. 检测其是否满足红黑树的性质
一般写验证的话要跟他的性质反着来,比如根节点的颜色是黑色的,那么如果根节点的颜色为红色就返回false
具体性质可以列为以下三条
根节点颜色为黑色
没有连续的红色节点
所有路径的黑色节点数量相同
根节点颜色为黑色已经讲过了
没有连续的红色节点可以在走中序的同时判断,(cur为遍历节点)若cur的颜色为红色且cur的parent的颜色也为红色那么返回false
至于所有路径的黑色节点数量相同
可以先统计一下最左路径黑色节点的数量作为参考值,然后如果有哪条路径的黑色节点数量不等于这个参考值的话就返回false
bool IsValidRBTRee()
{if (_root && _root->_col == RED){return false;}int refBlackNum = 0;//黑节点参考值Node* cur = _root;while (cur){if (cur->_col == BLACK){refBlackNum++;}cur = cur->_left;}return _IsValidRBTRee(_root, 0, refBlackNum);
}bool _IsValidRBTRee(Node* cur, size_t blackCount, size_t refBlack)
{if (cur == nullptr){if (refBlack != blackCount){cout << "黑色节点不相等" << endl;return false;}return true;}if (cur->_col == RED && cur->_parent->_col == RED){cout << "存在连续红色节点" << endl;return false;}if (cur->_col == BLACK)blackCount++;return _IsValidRBTRee(cur->_left, blackCount, refBlack)&& _IsValidRBTRee(cur->_right, blackCount, refBlack);
}3.全部代码
#pragma once
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv); // 红色的if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 情况一:叔叔存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else{// 情况二:叔叔不存在或者存在且为黑// 旋转+变色if (cur == parent->_left){RotateR(grandfather); // gparent->_col = BLACK; // p ugrandfather->_col = RED; // c}else{RotateL(parent);RotateR(grandfather); // gcur->_col = BLACK; // p ugrandfather->_col = RED; // c}break;}}else{Node* uncle = grandfather->_left;// 情况一:叔叔存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{// 情况二:叔叔不存在或者存在且为黑if (cur == parent->_right){RotateL(grandfather); // gparent->_col = BLACK; // u pgrandfather->_col = RED; // c}else{RotateR(parent);RotateL(grandfather); // gcur->_col = BLACK; // u pgrandfather->_col = RED; // c}break;}}}_root->_col = BLACK;return true;}/*获取红黑树最左侧节点*/Node* LeftMost(){Node* cur = _root;if (cur == nullptr ){return _root;}while (cur->_left){cur = cur->_left;}return cur;}// 获取红黑树最右侧节点Node* RightMost(){Node* cur = _root;if (nullptr == cur){return _root;}while (cur->_right){cur = cur->_right;}return cur;}// 检测红黑树是否为有效的红黑树,注意:其内部主要依靠_IsValidRBTRee函数检测bool IsValidRBTRee(){if (_root && _root->_col == RED){return false;}int refBlackNum = 0;//黑节点参考值Node* cur = _root;while (cur){if (cur->_col == BLACK){refBlackNum++;}cur = cur->_left;}return _IsValidRBTRee(_root, 0, refBlackNum);}void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first<<" ";_InOrder(root->_right);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}bool _IsValidRBTRee(Node* cur, size_t blackCount, size_t refBlack){if (cur == nullptr){if (refBlack != blackCount){cout << "黑色节点不相等" << endl;return false;}return true;}if (cur->_col == RED && cur->_parent->_col == RED){cout << "存在连续红色节点" << endl;return false;}if (cur->_col == BLACK)blackCount++;return _IsValidRBTRee(cur->_left, blackCount, refBlack)&& _IsValidRBTRee(cur->_right, blackCount, refBlack);}
private:Node* _root = nullptr;
};void TestRBTree1()
{int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16,10,12};RBTree<int,int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrder();cout << t.IsValidRBTRee() << endl;
}相关文章:

map和set(三)——红黑树
1、红黑树的概念及性质 1.1概念 概念: 红黑树是一种二叉搜索树,以颜色(Red or Black)互斥来限制每条路径不会比另外的路径长出两倍,来达到近似平衡 1.2性质 红黑树的性质: 每个节点不是黑色就是红色根节点是黑色的如果一个节点是…...

Day26 HashMap
Day26 HashMap 文章目录 Day26 HashMap一、应用场景二、特点三、基本用法四、面试题 一、应用场景 1、概念: HashMap是Java集合框架中的一种实现类,用于存储键值对。 2、好处: HashMap是一个常用的集合类,适用于需要快速查找和插…...

某蓝队面试经验
背景 据小道消息说今年的国护疑似提前到了五月份,所以最近也是HW面试的一个高峰期啊,这里分享一下上次长亭的蓝队面试问题(附本人的回答,仅供参考) 面试问答 1、谈谈作为蓝队护网过程使用过厂商的设备 这里我回答的…...
【Linux】 centos7安装卸载SQL server(2017、2019)
一、安装配置 准备一个基础Linux配置: 内存为20GB 运行内存为2GB的系统(数据库小于2GB安装不了) 1、网络配置 我们需要进行网络的连接 进入 cd /ect/sysconfig/network-script/ 编辑文件ifcfg-ens33 vi ifcfg-ens33 Insert键进行编辑 把ONBOO…...

面试算法-110-课程表
题目 你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。 …...

注册前后端php的检测
首先,在HTML表单中添加一个用于输入密码的文本框,并在其后面添加一个用于显示密码格式要求提示的元素,例如一个 <span> 标签。 <input type"password" id"passwordInput"> <span id"passwordHint…...

Redis:什么是redis?①
一、思想 Redis是一个开源的高性能基于内存key-value数据库,常用作数据库、缓存或消息代理 二、数据类型 String List...

【课程】MyBatisPlus视频教程
MyBatis-Plus是一款非常强大的MyBatis增强工具包,只做增强不做改变. 在不用编写任何SQL语句的情况下即可以极其方便的实现单一、批量、分页等操作。 本套教程基于MyBatis-Plus新2.3版本,详细讲授:集成Mybatis-Plus、 通用CRUD、EntityWrapper条件构造器、ActiveRec…...

如何使用人工智能和ChatGPT来优化营销转化率
人工智能 (AI) 和营销的交集正在彻底改变企业与客户互动的方式,最终改变营销转化率。人工智能能够分析大量数据、理解模式和自动执行任务,它不仅是一项创新技术,而且是营销领域的根本性转变。这种转变允许更加个性化、…...

Ubuntu 22.04上构建libvirt源码错误解决
当在Ubuntu 22.04上构建libvirt源码时,可能会遇到一些错误。下面是一些常见错误及其解决方法: 1. 错误:Program xmllint’未找到或不可执行 解决方法:安装libxml2-utils sudo apt-get install libxml2-utils2. 错误:…...

游戏客户端面经
1,3D的模型怎么显示到2DUI上面 2,C#的ArryList和List的区别 3,接口和抽象类的区别,一般什么时候用接口 4,UGUI怎么渲染的UI,UGUI的层级管理(怎么不打断合批),合批流程…...

AS,idea,maven,gradle
Jdk,sdk。提前都是需要下好的。 Maven与gradle的思考: 用AS开发app时,gradle本就有,自己也可以指定,AGP同样。要注意gradle,AGP,jdk版本的事情。还有依赖库。 用idea开发网络程序时,也有内置的maven&…...

ElasTool v3.0 程序:材料弹性和机械性能的高效计算和可视化工具包
分享一个材料弹性和机械性能的高效计算和可视化工具包: ElasTool v3.0。 感谢论文的原作者! 主要内容 “弹性和机械性能的高效计算和可视化对于材料的选择和新材料的设计至关重要。该工具包标志着材料弹性和机械性能计算分析和可视化方面的重大进步…...

Redis入门级详解(一)
一、Redis入门介绍 1、什么是Redis? Redis,英文全称是Remote Dictionary Server(远程字典服务),是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库,并提供多种语言的API。…...

java算法题每日多道六
138. 随机链表的复制 题目 给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。 构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对…...
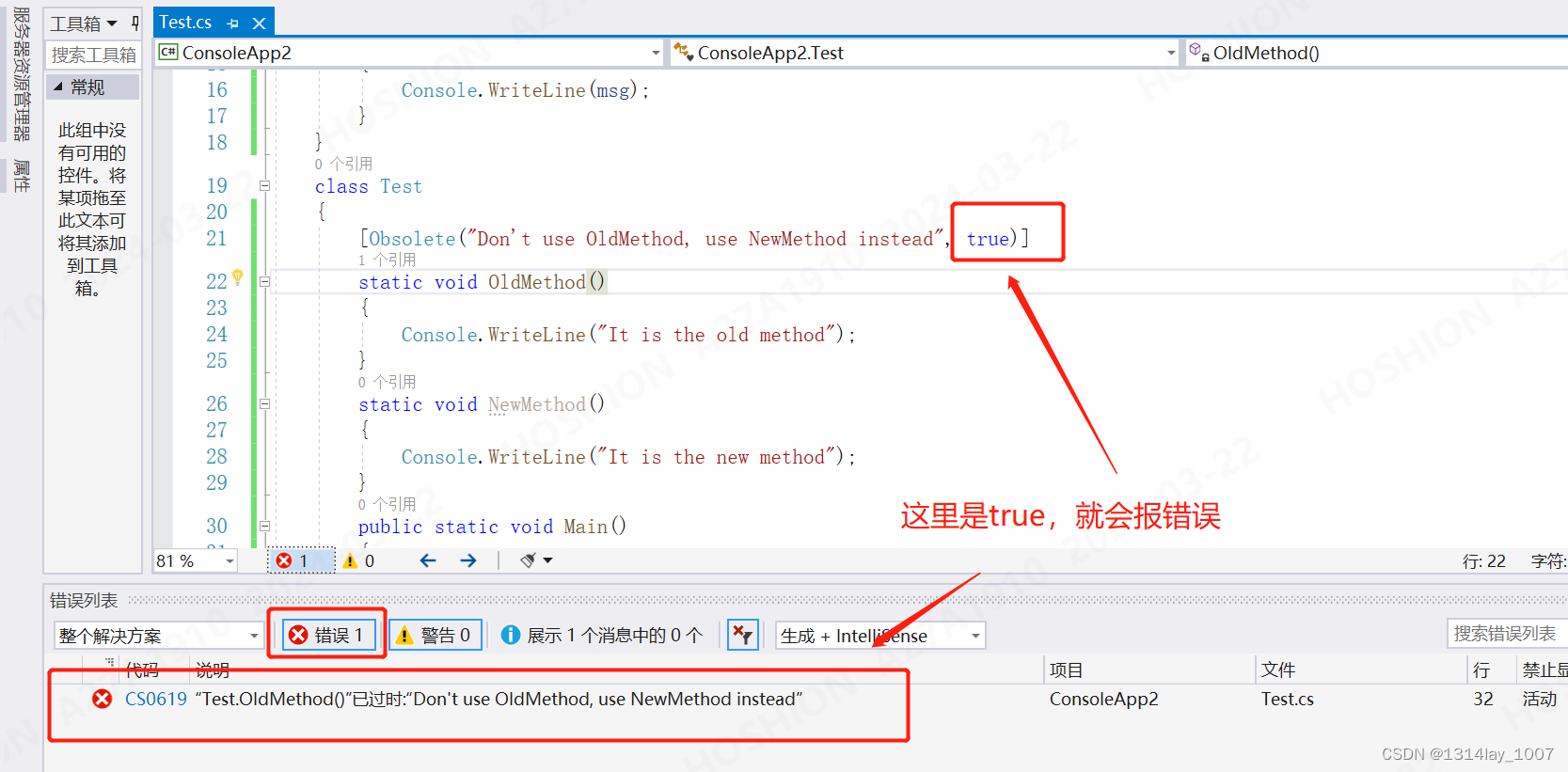
C# 特性(Attribute)
C# 特性(Attribute) 文章目录 C# 特性(Attribute)Obsolete语法示例代码 创建自定义特性(Attribute) Obsolete 这个预定义特性标记了不应被使用的程序实体。它可以让您通知编译器丢弃某个特定的目标元素。例…...
)
Redis 教程系列之Redis 配置(三)
Redis 配置 Redis 的配置文件位于 Redis 安装目录下,文件名为 redis.conf(Windows 名为 redis.windows.conf)。 你可以通过 CONFIG 命令查看或设置配置项。 语法 Redis CONFIG 命令格式如下: redis 127.0.0.1:6379> CONFIG GET CONFIG_SETTING_NAME 实例 redis 127.0…...

Java实验03
Code1 package q3;public class Method01{public static void main(String[] args) {class Student{String name;String StuID;public Student(String name,String StuID){this.namename;this.StuIDStuID;}public void speak(String name, String stuID) {//输出学号与姓名Sys…...
安卓studio连接手机之后,一两秒之后就自动断开了。问题解决。
太坑了,安卓studio链接手机之后。几秒之后就断开了。我以为是adb的问题,就重新安装了一下adb。并且在环境变量中配置了Path的路径。然而并没有什么用啊。 经过排查原来是数据心虚了。线的接触不良。导致你刚接通的瞬间有相对较强的电流是因为有瞬间高电压…...

数字科技优化金融供给,内外协同激活新质生产力
来源 | 镭射财经(leishecaijing) 新一轮产业变革悄然发生,决定产业高度和竞争格局的底层生产力,也正在经历一场从量变到质变的跃迁。新质生产力则是这场跃迁后的最新呈现。 站在新质生产力爆发的时代拐点,金融业达成…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
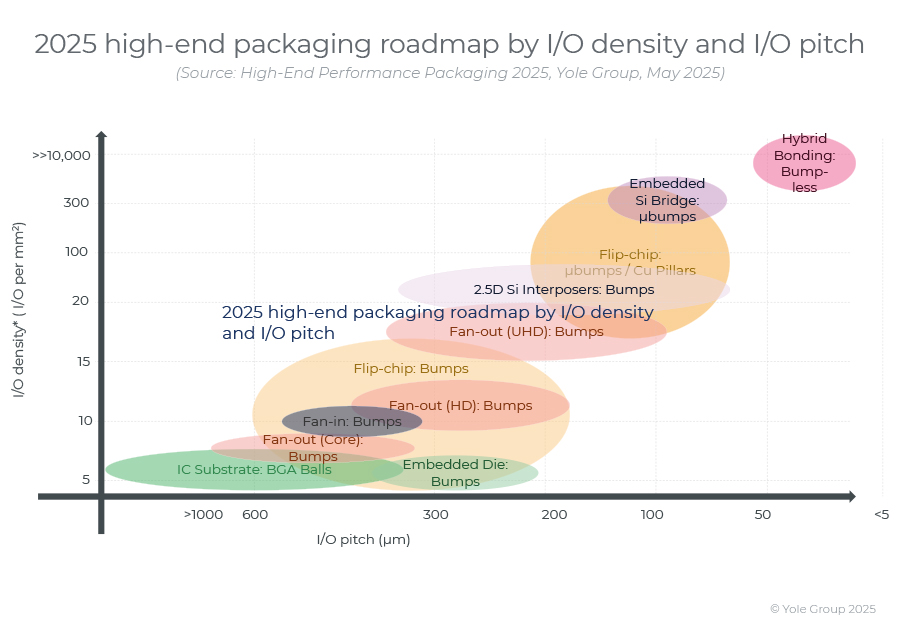
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...
