PTA L2-032 彩虹瓶

彩虹瓶的制作过程(并不)是这样的:先把一大批空瓶铺放在装填场地上,然后按照一定的顺序将每种颜色的小球均匀撒到这批瓶子里。
假设彩虹瓶里要按顺序装 N 种颜色的小球(不妨将顺序就编号为 1 到 N)。现在工厂里有每种颜色的小球各一箱,工人需要一箱一箱地将小球从工厂里搬到装填场地。如果搬来的这箱小球正好是可以装填的颜色,就直接拆箱装填;如果不是,就把箱子先码放在一个临时货架上,码放的方法就是一箱一箱堆上去。当一种颜色装填完以后,先看看货架顶端的一箱是不是下一个要装填的颜色,如果是就取下来装填,否则去工厂里再搬一箱过来。
如果工厂里发货的顺序比较好,工人就可以顺利地完成装填。例如要按顺序装填 7 种颜色,工厂按照 7、6、1、3、2、5、4 这个顺序发货,则工人先拿到 7、6 两种不能装填的颜色,将其按照 7 在下、6 在上的顺序堆在货架上;拿到 1 时可以直接装填;拿到 3 时又得临时码放在 6 号颜色箱上;拿到 2 时可以直接装填;随后从货架顶取下 3 进行装填;然后拿到 5,临时码放到 6 上面;最后取了 4 号颜色直接装填;剩下的工作就是顺序从货架上取下 5、6、7 依次装填。
但如果工厂按照 3、1、5、4、2、6、7 这个顺序发货,工人就必须要愤怒地折腾货架了,因为装填完 2 号颜色以后,不把货架上的多个箱子搬下来就拿不到 3 号箱,就不可能顺利完成任务。
另外,货架的容量有限,如果要堆积的货物超过容量,工人也没办法顺利完成任务。例如工厂按照 7、6、5、4、3、2、1 这个顺序发货,如果货架够高,能码放 6 只箱子,那还是可以顺利完工的;但如果货架只能码放 5 只箱子,工人就又要愤怒了……
本题就请你判断一下,工厂的发货顺序能否让工人顺利完成任务。
输入格式:
输入首先在第一行给出 3 个正整数,分别是彩虹瓶的颜色数量 N(1<N≤103)、临时货架的容量 M(<N)、以及需要判断的发货顺序的数量 K。
随后 K 行,每行给出 N 个数字,是 1 到N 的一个排列,对应工厂的发货顺序。
一行中的数字都以空格分隔。
输出格式:
对每个发货顺序,如果工人可以愉快完工,就在一行中输出 YES;否则输出 NO。
输入样例:
7 5 3
7 6 1 3 2 5 4
3 1 5 4 2 6 7
7 6 5 4 3 2 1
输出样例:
YES
NO
NO做法:
其实货架就是一个栈,发货顺序可以看成一个队列。
1.初始化队列
2.判断是否可以完工
代码:
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>using namespace std;const int N = 1010;int stock[N],color[N];
int n,m;bool check()
{int c = 1,top = -1;for(int i = 0;i < n;i++){if(color[i] == c)//可以装填{c++;while(top >= 0 && stock[top] == c) top--,c++;//去货架上看看}else{if(top < m - 1) stock[++top] = color[i];else return false;//放不下}}if(c == n + 1) return true;//完成任务else return false;
}
int main()
{int k = 0;scanf("%d%d%d",&n,&m,&k);for(int i = 0;i < k;i++){for(int j = 0;j < n;j++) scanf("%d",&color[j]);//存储发货顺序if(check()) puts("YES");else puts("NO");}return 0;
}结果:
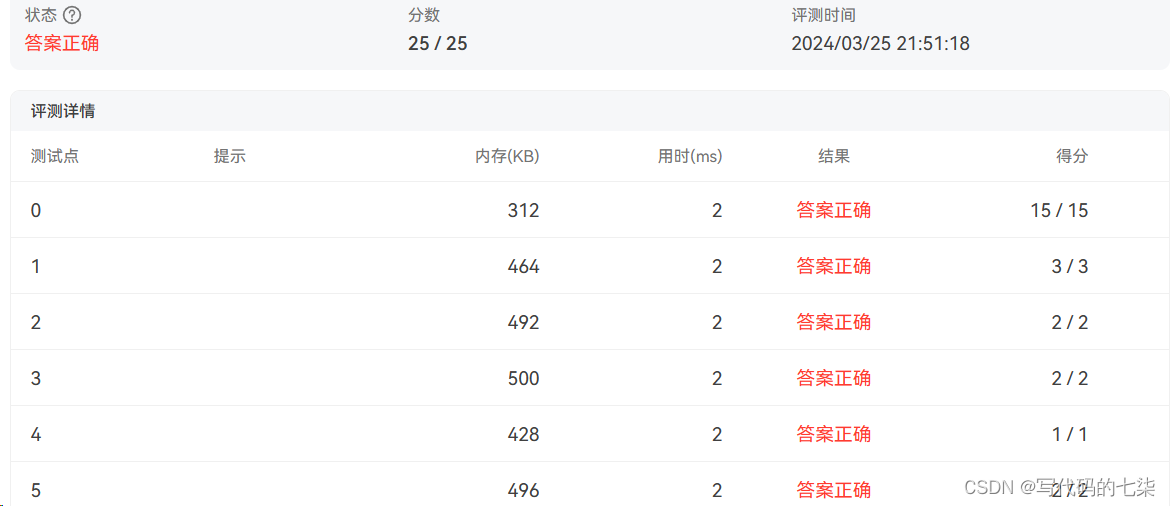
相关文章:

PTA L2-032 彩虹瓶
彩虹瓶的制作过程(并不)是这样的:先把一大批空瓶铺放在装填场地上,然后按照一定的顺序将每种颜色的小球均匀撒到这批瓶子里。 假设彩虹瓶里要按顺序装 N 种颜色的小球(不妨将顺序就编号为 1 到 N)。现在工…...

Spring和Spring Boot之间的区别
Spring和Spring Boot之间的区别 不仅仅体现在操作简化、配置方式以及开发速度上,还有以下几个方面: 模块化和功能范围: Spring是一个完整的框架,提供了各种各样的功能,包括依赖注入、面向切面编程、数据访问、事务管…...

海外客户获取难?海外云手机助力电商引流!
海外电商面临的市场竞争激烈,如何在海外市场获客成为了摆在许多卖家面前的难题。而在这个问题的解决方案中,海外云手机崭露头角,成为助力电商引流的新利器。 在当前市场中,云手机主要用于游戏挂机,但其潜力在海外电商领…...

什么情况下 C++ 需要垃圾处理机制?
C,作为一种以性能和灵活性著称的编程语言,历来以其严谨的手动内存管理而闻名。然而,尽管C提供了丰富的工具如RAII(Resource Acquisition Is Initialization)原则、智能指针等来协助开发者有效地管理内存,但…...
流畅的 Python 第二版(GPT 重译)(七)
第十三章:接口、协议和 ABCs 针对接口编程,而不是实现。 Gamma、Helm、Johnson、Vlissides,《面向对象设计的第一原则》 面向对象编程关乎接口。在 Python 中理解类型的最佳方法是了解它提供的方法——即其接口——如 “类型由支持的操作定义…...

vue项目中使用vue-pdf或pdf.Js,实现在页面上预览pdf内容
一。vue-pdf 1. 安装vue-pdf npm install --save vue-pdf2.页面引入 js部分 import pdf from "vue-pdf";data(){return {pdfUrl: "",pageTotal: 0,} }mounted(){this.pdfUrl pdf.createLoadingTask(pdf文件路径url);// 获取页码this.pdfUrl.promise…...
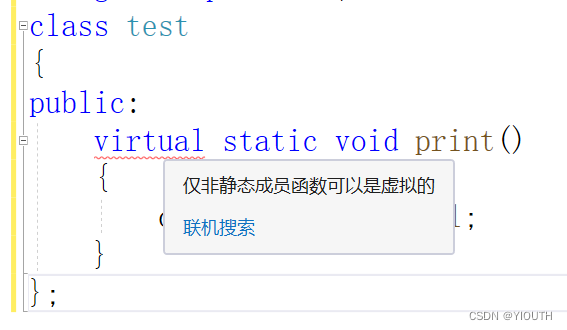
为什么静态成员函数不能是虚函数
在面向对象编程中,静态成员函数和虚函数都是常见的概念,但它们之间存在着本质上的差异。由于其特性上的差异,静态成员函数不能声明为虚函数。下面我们来探讨一下为什么静态成员函数不能是虚函数。 我在网上查到最多的说法是静态函数没有this指…...
)
python环境移植(本机windows到离线windows环境)
Python环境整体迁移(包括无网络情况)_python 迁移 新老无法联网-CSDN博客...

蓝桥杯day9刷题日记
P8649 [蓝桥杯 2017 省 B] k 倍区间 思路:前缀和的题,对k取余相同的数就可以得到k的倍数 #include <iostream> #include <string> using namespace std; long long ans; int n,k; long long q[100010]; long long sum[100010];int main() …...

阿里云数据库Cassandra的产品价格
本文介绍阿里云数据库Cassandra的价格。 支持的地域 当前开通的地域如下: 中国站点:华东1(杭州)、华东2(上海)、华南1(深圳)、华北1(青岛)、华北2ÿ…...

离散制造企业MES与流程企业MES的区别
制造行业根据加工过程管控主要分为两大类:离散型与流程型。 离散型主要是通过对原材料的物理形状改进或组合,使其成为产品并增值,如机械加工、家用电器、电子电气行业等。 流程型则主要是采用物料或化学的方法对原材料进行混合、分离、加热…...

中国象棋C++
题目描述 在中国象棋中正所谓新手玩车,熟手玩炮,老手玩马,由此可见象棋中炮的地位还是比较高的。 给定一个nm的棋盘,全部摆满炮,我们视所有炮都不属于同一阵营,他们之间可以相互攻击但不能不进行攻击直接移…...
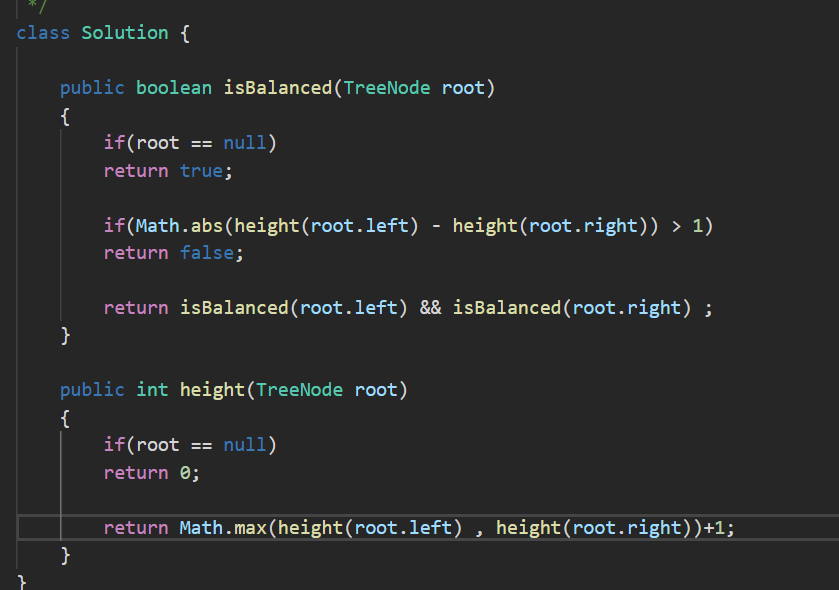
记录一下目前为止的算法成长
每日笔记 复习曲线 间隔1天、3天、7天、15天、30天,然后以一个月为周期复习 2023. 12. 24 一定要每天早中晚都要复习一下 早中午每段一两道, 而且一定要是同一个类型, 不然刷起来都没有意义 11.29 开始向着面试刷题跟进! 每天刷4题左右 ,一周之内一定要是统一类…...

AI大模型学习在数控系统工艺优化与智能制造中的应用
目录 1.工艺优化: 2.预测维护: 3.质量控制: 4.自动编程: 5.人机协作: 6.系统集成: AI大模型学习在数控系统工艺优化与智能制造中的应用主要体现在以下几个方面: 1.工艺优化: …...
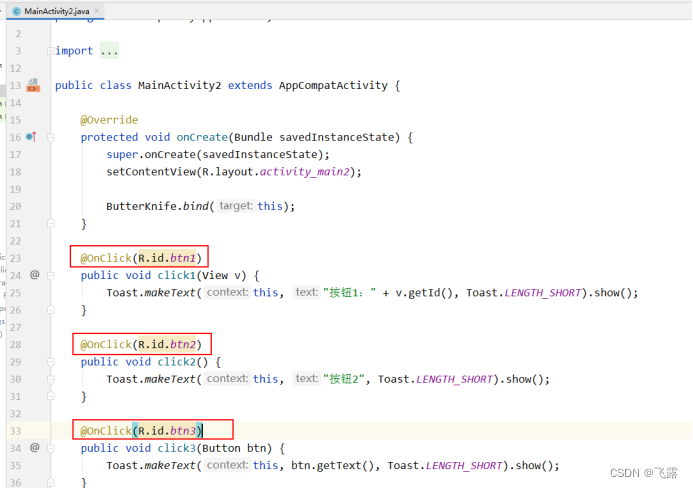
安卓findViewById 的优化方案:ViewBinding与ButterKnife(一)
好多小伙伴现在还用findViewById来获取控件的id, 在这里提供俩种替代方案:ViewBinding与ButterKnife; 先来说说ButterKnife ButterKnife ButterKnife是一个专注于Android系统的View注入框架,在过去的项目中总是需要很多的findViewById来查…...
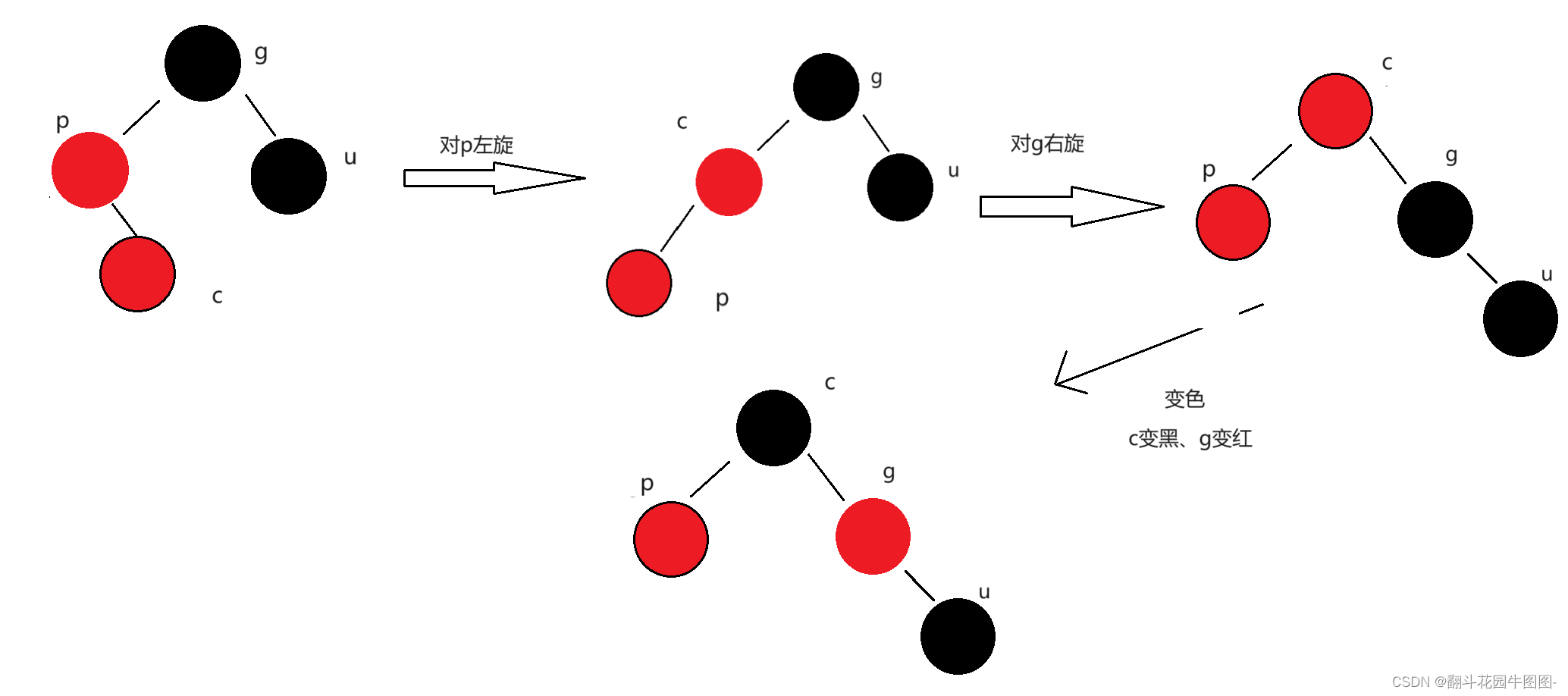
map和set(三)——红黑树
1、红黑树的概念及性质 1.1概念 概念: 红黑树是一种二叉搜索树,以颜色(Red or Black)互斥来限制每条路径不会比另外的路径长出两倍,来达到近似平衡 1.2性质 红黑树的性质: 每个节点不是黑色就是红色根节点是黑色的如果一个节点是…...

Day26 HashMap
Day26 HashMap 文章目录 Day26 HashMap一、应用场景二、特点三、基本用法四、面试题 一、应用场景 1、概念: HashMap是Java集合框架中的一种实现类,用于存储键值对。 2、好处: HashMap是一个常用的集合类,适用于需要快速查找和插…...

某蓝队面试经验
背景 据小道消息说今年的国护疑似提前到了五月份,所以最近也是HW面试的一个高峰期啊,这里分享一下上次长亭的蓝队面试问题(附本人的回答,仅供参考) 面试问答 1、谈谈作为蓝队护网过程使用过厂商的设备 这里我回答的…...
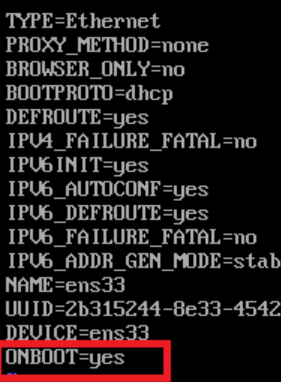
【Linux】 centos7安装卸载SQL server(2017、2019)
一、安装配置 准备一个基础Linux配置: 内存为20GB 运行内存为2GB的系统(数据库小于2GB安装不了) 1、网络配置 我们需要进行网络的连接 进入 cd /ect/sysconfig/network-script/ 编辑文件ifcfg-ens33 vi ifcfg-ens33 Insert键进行编辑 把ONBOO…...

面试算法-110-课程表
题目 你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。 …...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
