蓝桥杯刷题_day1_回文数_水仙花数_进制转换
文章目录
- 特殊的回文数
- 回文数
- 水仙花数
- 十六进制转八进制_n次
特殊的回文数
问题描述
123321是一个非常特殊的数,它从左边读和从右边读是一样的。
输入一个正整数n, 编程求所有这样的五位和六位十进制数,满足各位数字之和等于n 。
解题思路
1.将数字转化为字符串,判断这个字符串是否为回文串
2.将数字进行逆转,然后判断与原数字是否相等
3.将数字的一半进行逆转没然后判断是否与原串是否相同。
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;int palindromicNumber(int pn)
{string tmp = to_string(pn);string reverse_tmp(tmp);reverse(reverse_tmp.begin(), reverse_tmp.end());if (tmp == reverse_tmp){return 1;}else{return 0;}
}int main()
{int n = 0;cin >> n;for (int i = 10000; i <= 999999; i++){if (palindromicNumber(i)){int tmp = i;int sum = 0;while (tmp){sum = sum + tmp % 10;tmp /= 10;}if (sum == n){cout << i << endl;}}}return 0;
}
回文数
问题描述
1221是一个非常特殊的数,它从左边读和从右边读是一样的,编程求所有这样的四位十进制数。
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;//将数字转为字符串,之后将字符串进行逆转,然后判断两个字符串是否相同 int palindromicNumber(int pn)
{string tmp;while(pn){tmp.insert(0,1,(pn%10) + '0');pn/=10;}string reverse_tmp(tmp);reverse(reverse_tmp.begin(),reverse_tmp.end());if(reverse_tmp == tmp){return 1;}else{return 0;}
}int main()
{int i;for(i = 1000;i<= 9999;i++){if(palindromicNumber(i)){cout << i << endl;}}return 0;
}水仙花数
问题描述
153是一个非常特殊的数,它等于它的每位数字的立方和,即153=111+555+333。编程求所有满足这种条件的三位十进制数。
#include<iostream>
#include<string>
#include<algorithm>
#include<math.h>
using namespace std;int sameSum(int n)
{int sum = 0;int tmp = n;while(n){sum = sum + pow(n%10,3);n/=10;}if(tmp == sum){return 1;}else{return 0;}
}int main()
{int i;for(i=100;i<=999;i++){if(sameSum(i)){cout << i << endl;}}return 0;
}
十六进制转八进制_n次
问题描述
给定n个十六进制正整数,输出它们对应的八进制数。
输入格式
输入的第一行为一个正整数n (1<=n<=10)。
接下来n行,每行一个由09、大写字母AF组成的字符串,表示要转换的十六进制正整数,每个十六进制数长度不超过100000。
输出格式
输出n行,每行为输入对应的八进制正整数。
【注意】
输入的十六进制数不会有前导0,比如012A。
输出的八进制数也不能有前导0。
#include<iostream>
#include<string>
#include<math.h>
using namespace std;//十六进制转十进制
int hexToDec(string hex)
{int dec = 0;int pows = 0;for (int i = hex.length() - 1; i >= 0; i--){char c = hex[i];if (c >= '0' && c <= '9'){dec = (c - '0') * pow(16, pows) + dec;}else{dec = (c - 'A' + 10) * pow(16, pows) + dec;}pows++;}return dec;
}//十进制转八进制
int decToOct(int dec)
{int oct = 0;int i = 1;while (dec){oct = oct + dec % 8 * i;dec = dec / 8;i *= 10;}return oct;
}int main()
{int count = 0;cin >> count;string hex[10];for (int i = 0; i < count; i++){cin >> hex[i];}for (int i = 0; i < count; i++){int tmp = hexToDec(hex[i]);cout << decToOct(tmp) << endl;}return 0;
}
相关文章:

蓝桥杯刷题_day1_回文数_水仙花数_进制转换
文章目录 特殊的回文数回文数水仙花数十六进制转八进制_n次 特殊的回文数 问题描述 123321是一个非常特殊的数,它从左边读和从右边读是一样的。 输入一个正整数n, 编程求所有这样的五位和六位十进制数,满足各位数字之和等于n 。 解题…...
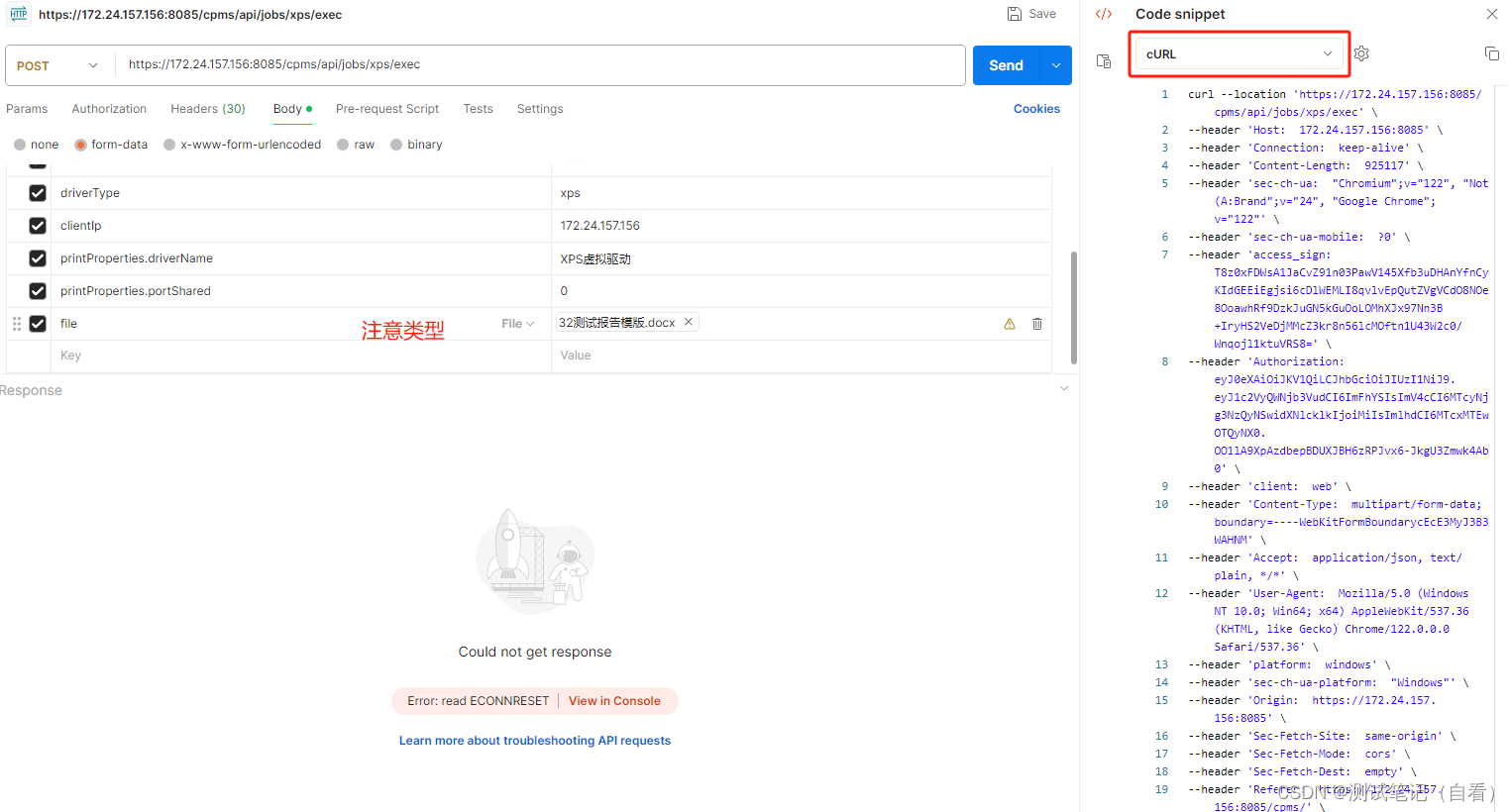
jmeter接口导入方式
curl直接导入 1、操作页面后,F12查看接口,右击接口-copy-copy as cURL 2、jmeter 工具-import from cURL,粘贴上面复制的curl 根据接口文档导入 1、接口文档示例如下: Path: /api/jobs/xps/exec Method…...
)
设计模式(行为型设计模式——状态模式)
设计模式(行为型设计模式——状态模式) 状态模式 基本定义 对有状态的对象,把复杂的“判断逻辑”提取到不同的状态对象中,允许状态对象在其内部状态发生改变时改变其行为。 模式结构 Context(环境类)&…...

【Flutter学习笔记】10.3 组合实例:TurnBox
参考资料:《Flutter实战第二版》 10.3 组合实例:TurnBox 这里尝试实现一个更为复杂的例子,其能够旋转子组件。Flutter中的RotatedBox可以旋转子组件,但是它有两个缺点: 一是只能将其子节点以90度的倍数旋转二是当旋转…...

性能测试入门 —— 什么是性能测试PTS?
性能测试PTS(Performance Testing Service)是一款简单易用,具备强大的分布式压测能力的SaaS压测平台。 PTS可以模拟复杂的业务场景,并快速精准地调度不同规模的流量,同时提供压测过程中多维度的监控指标和日志记录。您…...
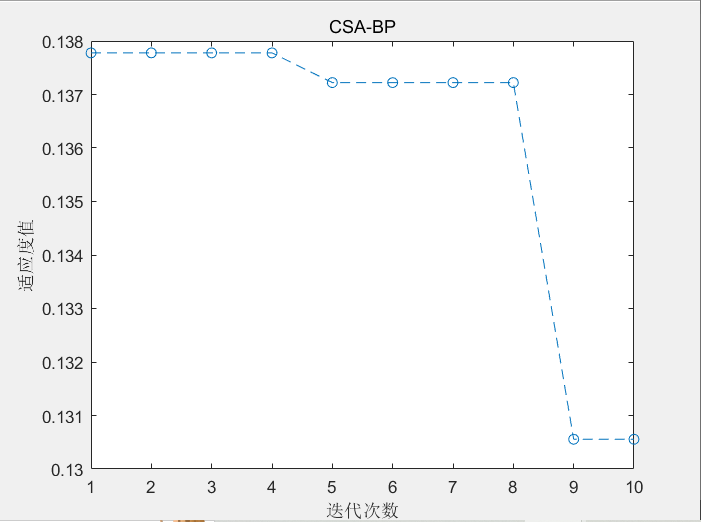
【机器学习】基于变色龙算法优化的BP神经网络分类预测(SSA-BP)
目录 1.原理与思路2.设计与实现3.结果预测4.代码获取 1.原理与思路 【智能算法应用】智能算法优化BP神经网络思路【智能算法】变色龙优化算法(CSA)原理及实现 2.设计与实现 数据集: 数据集样本总数2000 多输入多输出:样本特征24ÿ…...

pytorch中tensor类型转换的几个函数
目录 IntTensor转FloatTensor FloatTensor转IntTensor Tensor类型变为python的常规类型 IntTensor转FloatTensor .float函数: FloatTensor转IntTensor .int函数 Tensor类型变为python的常规类型 item函数...

深入理解Elasticsearch高效原理
在当今数据驱动的世界中,能够快速有效地存储、搜索和分析庞大数据集变得至关重要。Elasticsearch是一个强大的开源搜索和分析引擎,专为云计算中心而设计,能够提供快速的搜索功能,并且能够扩展到包含数百个服务器的集群,…...

http和socks5代理哪个隐蔽性更强?
HTTP代理和SOCKS5代理各有其优缺点,但就隐蔽性而言,SOCKS5代理通常比HTTP代理更隐蔽。以下是它们的比较: HTTP代理: 透明性较高:HTTP代理在HTTP头中会透露原始客户端的IP地址,这使得它相对不太隐蔽。…...

邮箱的正则表达式
一、 背景 项目中要给用户发送邮件,这时候需要校验用户输入的邮箱的有有效性,这肯定用正则呀。 虽然没有统一的邮箱账号格式,但是所有邮箱都符合“名称域名”的规律。对于名称和域名的字符限制,我们可以根据项目的情况定义一个&a…...

blender插件笔记
目录 文件拖拽导入 smpl导入导出 好像可以导入动画 smpl_blender_addon导入一帧 保存pose 导入导出完整代码 文件拖拽导入 https://github.com/mika-f/blender-drag-and-drop 支持格式: *.abc*.bvh*.dae*.fbx*.glb*.gltf*.obj*.ply*.stl*.svg*.usd*.usda*.…...

解释关系型数据库和非关系型数据库的区别
一、解释关系型数据库和非关系型数据库的区别 关系型数据库和非关系型数据库在多个方面存在显著的区别。 首先,从数据存储方式来看,关系型数据库采用表格形式,数据存储在数据表的行和列中,且数据表之间可以关联存储,…...

YAML-02-yml 配置文件 java 整合使用 yamlbeans + snakeyaml + jackson-dataformat-yaml
java 中处理 yml 的开源组件是什么? 在Java中处理YAML(YAML Aint Markup Language)格式的开源组件有很多,其中一些比较常用的包括: SnakeYAML: SnakeYAML 是一个Java库,用于解析和生成YAML格式…...
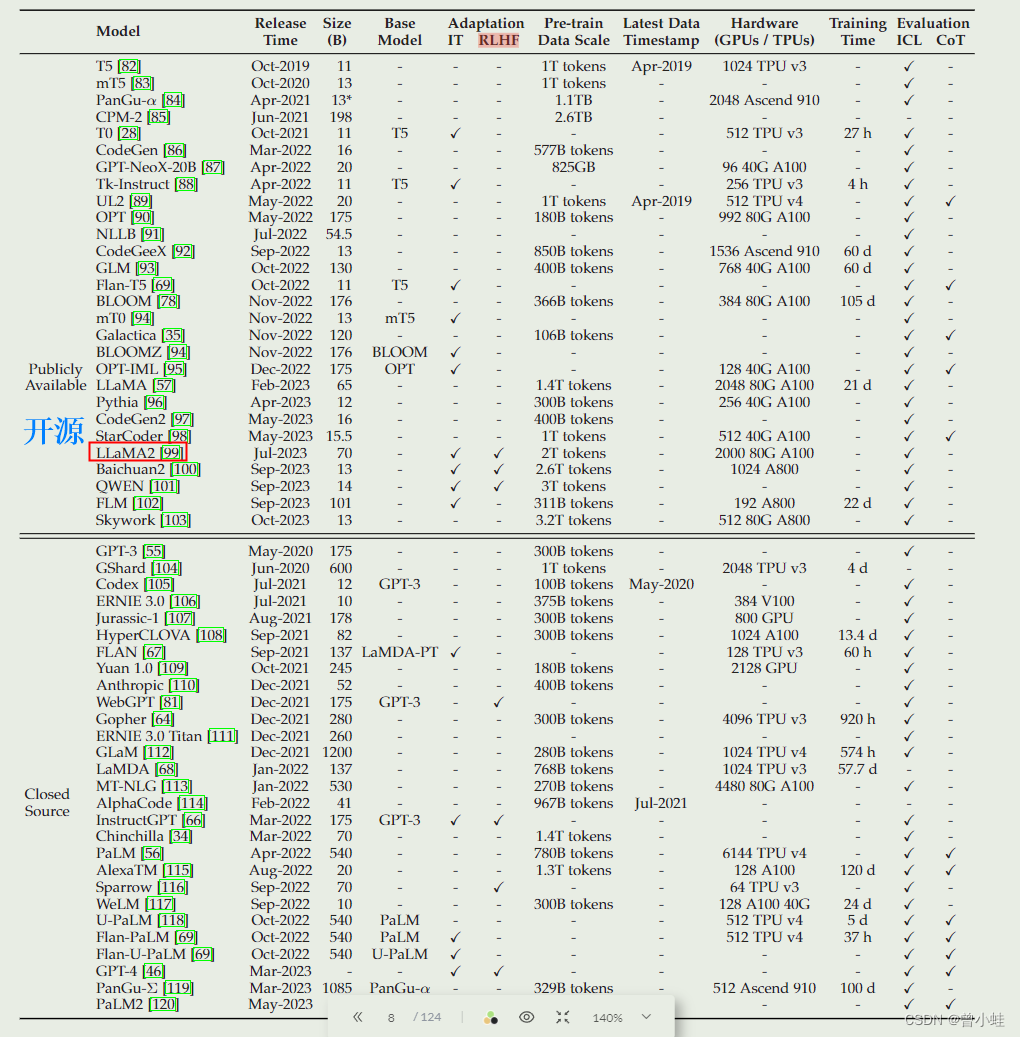
【综述+LLMs】国内团队大语言模型综述:A Survey of Large Language Models (截止2023.11.24)
Github主页: https://github.com/RUCAIBox/LLMSurvey 中文版v10:https://github.com/RUCAIBox/LLMSurvey/blob/main/assets/LLM_Survey_Chinese.pdf 英文版v13: https://arxiv.org/abs/2303.18223 解析:大语言模型LLM入门看完你就懂了(一&…...
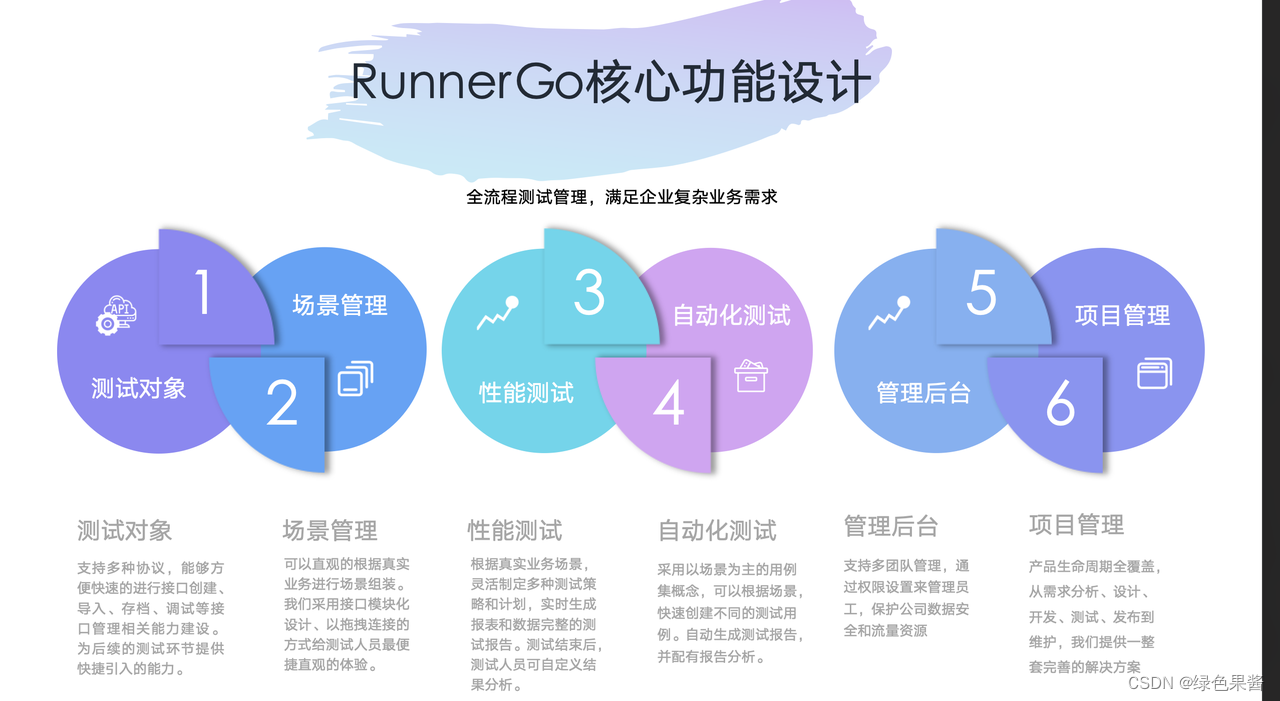
开始喜欢上了runnergo,JMeter out了?
RunnerGo是一款基于Go语言、国产自研的测试平台。它支持高并发、分布式性能测试。和JMeter不一样的是,它采用了B/S架构,更灵活、更方便。而且,除了API测试和性能测试,RunnerGo还加上了UI测试和项目管理等实用功能,让测…...
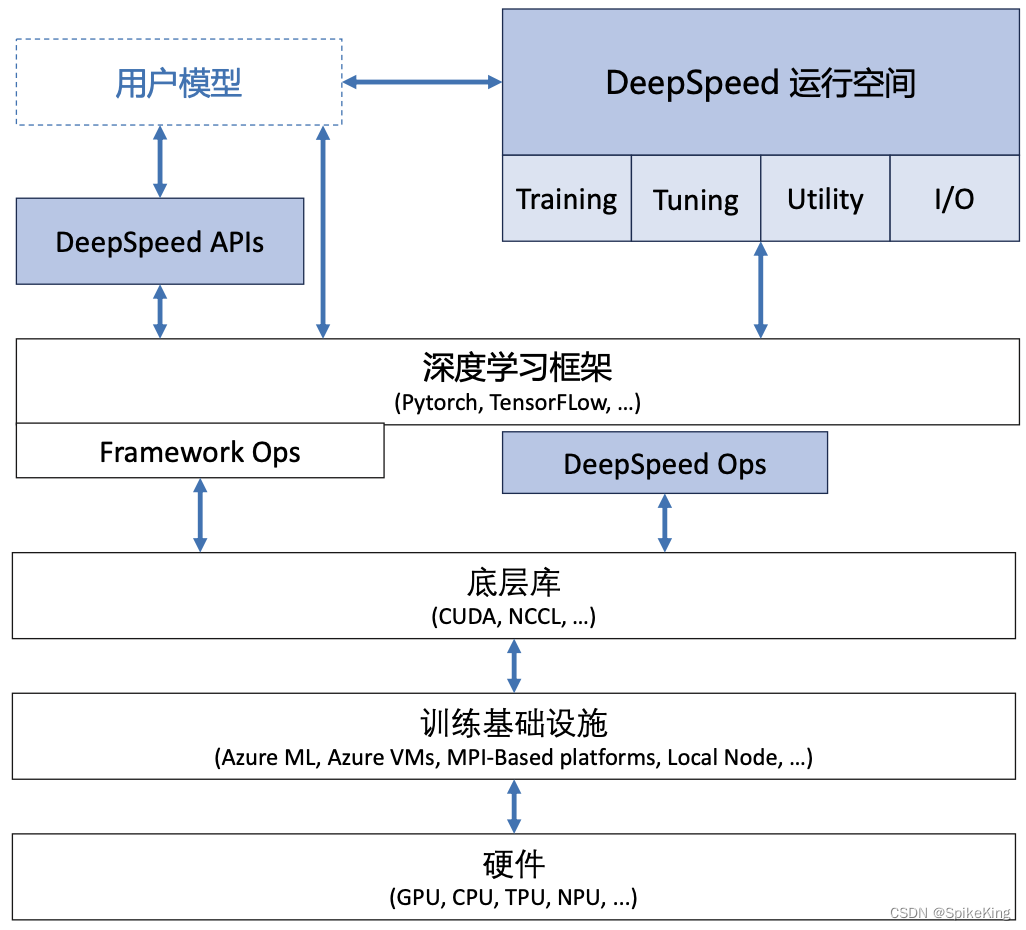
LLM - 大语言模型的分布式训练 概述
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://blog.csdn.net/caroline_wendy/article/details/136924304 大语言模型的分布式训练是一个复杂的过程,涉及到将大规模的计算任务分散到多个计算节点上。这样做的目的是为了处…...

Spring Cloud Alibaba 整合Seata分布式事务
目录 前言步骤引入相关maven依赖添加相关配置Client端配置注册中心Server端配置注册中心Seata-Server相关配置启动seata-server 使用方法Seata AT 模式整体机制 步骤初始化表结构标记注解GlobalTransactional 总结 前言 在数字化转型的浪潮下,企业业务系统的复杂度…...

unity 多屏幕操作
想了解基础操作请移步:(重点是大佬写的好,这里就不再赘述) Unity 基础 之 使用 Display 简单的实现 多屏幕显示的效果_unity display-CSDN博客 在panel上也可以通过获取 Canvas,来达到切换多屏幕的操作, …...

4、Jenkins持续集成-用户权限和凭证管理
文章目录 一、用户权限管理1、安装用户权限管理插件2、开启权限全局安全配置3、创建角色4、创建用户5、给用户分配角色6、创建项目测试权限二、凭证管理1、安装凭证管理插件2、安装Git插件和工具2.1 用户密码类型2.2 SSH密钥类型一、用户权限管理 利用Role-based Authorizatio…...

K8s-网络原理-中篇
引言 本文是《深入剖析 K8s》的学习笔记,相关图片和案例可从https://github.com/WeiXiao-Hyy/k8s_example中获取,欢迎 ⭐️! 上篇主要介绍了 Flannel 插件为例,讲解了 K8s 里容器网络和 CNI 插件的主要工作原理。还有一种“纯三层”的网络方…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
