智能合约 之 ERC-721
ERC-721(Non-Fungible Token,NFT)标准
ERC-721是以太坊区块链上的一种代币标准,它定义了一种非同质化代币(Non-Fungible Token,NFT)的标准。NFT是一种加密数字资产,每个代币都具有独特的属性,使其在区块链上不可互换。ERC-721标准的提出为数字艺术品、游戏物品、房地产和其他实物资产的数字化所有权提供了基础
基本原理
ERC-721标准建立在以太坊智能合约技术之上,它定义了一组规则,以确保非同质化代币的发行、传输和交易的一致性和互操作性。与传统的代币标准(如ERC-20)不同,ERC-721代币具有独一无二的标识符和属性,因此每个代币都是独特的
ERC-20属于同质化代币,比如 你的 1 USDT 和 `我的 1 USDT`` 本质上是一样的价值
应用场景
数字艺术品: 艺术家可以将其作品转换为ERC-721代币,并通过智能合约确保其数字版权。游戏物品: 游戏开发者可以使用ERC-721创建游戏中的唯一道具、角色或地图,玩家可以拥有、交易或出售这些物品。比如:加密猫房地产和虚拟现实: 开发者可以利用ERC-721创建虚拟地产,如数字土地或建筑,从而在虚拟现实世界中实现所有权和交易。
目前来看,游戏物品是最有发展潜力的。数字艺术品和房地产和虚拟现实一般需要公证机构的参与,所以有其局限性。

定义的规则
function balanceOf(address _owner) external view returns (uint256); // 拥有几个NFTfunction ownerOf(uint256 _tokenId) external view returns (address); // 谁拥有当前NFT(_tokenId)function safeTransferFrom(address _from, address _to, uint256 _tokenId, bytes data) external payable; // 转移NFTfunction safeTransferFrom(address _from, address _to, uint256 _tokenId) external payable; // 转移NFTfunction transferFrom(address _from, address _to, uint256 _tokenId) external payable; // 转移NFTfunction approve(address _approved, uint256 _tokenId) external payable; // 将自己的NFT授权给_approved,其可以执行转移操作function setApprovalForAll(address _operator, bool _approved) external; // 授权_approved可以转移自己所有此合约的NFTfunction getApproved(uint256 _tokenId) external view returns (address); // 检查某个NFT的转移权限function isApprovedForAll(address _owner, address _operator) external view returns (bool); // 检查_operator是否有_owner的NFT的转移权限关注我,一起进入Web3的世界
相关文章:

智能合约 之 ERC-721
ERC-721(Non-Fungible Token,NFT)标准 ERC-721是以太坊区块链上的一种代币标准,它定义了一种非同质化代币(Non-Fungible Token,NFT)的标准。NFT是一种加密数字资产,每个代币都具有独…...

== 和 equals 的区别是什么?
和 equals() 在 Java 中都是用于比较两个对象,但它们之间存在显著的差异: 比较的内容: :这是 Java 中的基本比较运算符,对于基本数据类型(如 int, char, double 等),它比较的是值&a…...

VUE:内置组件<Teleport>妙用
一、<Teleport>简介 <Teleport>能将其插槽内容渲染到 DOM 中的另一个位置。也就是移动这个dom。 我们可以这么使用它: 将class为boxB的盒子移动到class为boxA的容器中。 <Teleport to".boxA"><div class"boxB"></div> &…...

ruoyi-nbcio-plus后端里mapstruct-plus和lombok的使用
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 http://122.227.135.243:9666/ 更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码:…...

企业如何选择一个开源「好」项目?
开源 三句半 需求明确是关键 风险考量要周全 开源虽好不白捡 别忘合规! 显然,开源已成为一股不可阻挡的洪流,企业拥抱开源,积极参与开源项目不仅是响应技术潮流的必然选择,更是实现自身技术创新、市场拓…...
 并查集)
c++算法学习笔记 (14) 并查集
1.合并集合 一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。 现在要进行 m 个操作,操作共有两种: M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,…...

import * as的使用
import * as 是将一个模块的所有导出内容作为一个命名空间对象导入到当前模块中,其中 * 表示导入该模块中的所有导出内容,而 as 则用于指定导入的命名空间对象的名称。 例如:在 formatter 文件中有两个方法导出 const a () > {console.…...

微服务(基础篇-003-Nacos)
目录 Nacos注册中心(1) 认识和安装Nacos(1.1) Nacos快速入门(1.2) 服务注册到Nacos(1.2.1) Nacos服务分级存储模型(1.3) 配置集群(1.3.1) 根据集群修改…...
java数据结构与算法刷题-----LeetCode215. 数组中的第K个最大元素
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 文章目录 解题思路:时间复杂度O( n n n),空间复杂度…...

Springboot 整合 Knife4j (API文档生成工具)
目录 一、Knife4j 介绍 二、Springboot 整合 Knife4j 1、pom.xml中引入依赖包 2、在application.yml 中添加 Knife4j 相关配置 3、打开 Knife4j UI界面 三、关于Knife4j框架中常用的注解 1、Api 2、ApiOperation 3、ApiOperationSupport(order X) 4、ApiImplici…...
C语言---------strlen的使用和模拟实现
字符串是以‘\0’作为结束标志,strlen函数的返回值是‘\0’前面的字符串的个数(不包括‘\0’) 注意 1,参数指向的字符串必须以‘\0’结束 2,函数的返回值必须以size_t,是无符号的 使用代码 #include<stdio.…...
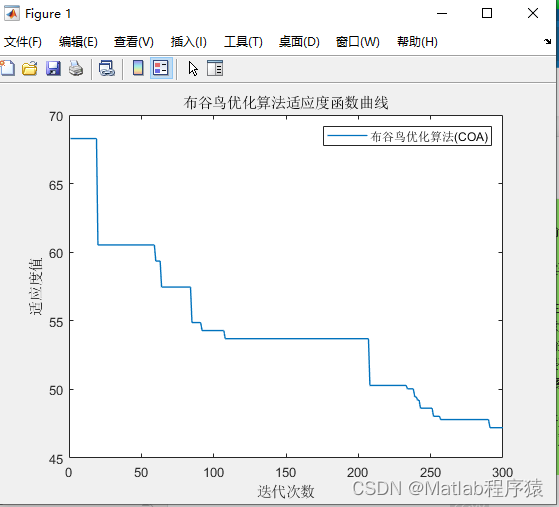
【MATLAB源码-第168期】基于matlab的布谷鸟优化算法(COA)机器人栅格路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 布谷鸟优化算法(Cuckoo Optimization Algorithm, COA)是一种启发式搜索算法,其设计灵感源自于布谷鸟的独特生活习性,尤其是它们的寄生繁殖行为。该算法通过模拟布谷鸟在自然界中…...
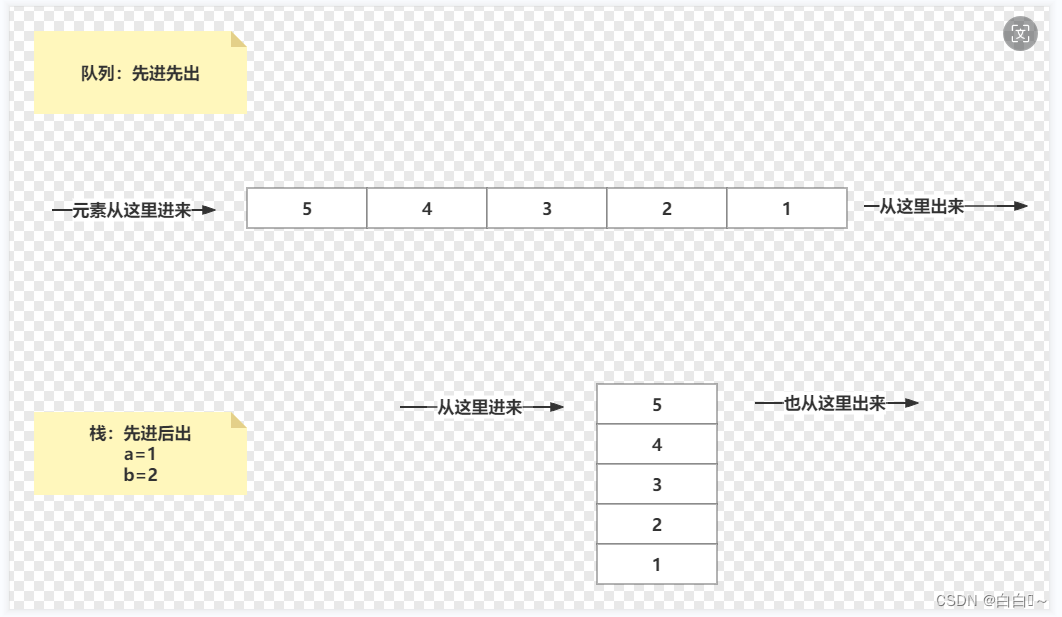
集合深入------理解底层。
集合的使用 前提:栈、堆、二叉树、hashcode、toString()、quesalus()的知识深入和底层理解。 1、什么是集合 集合就是咋们所说的容器 前面我们学习过数组 数组也是容器 容器:装东西的 生活中有多少的容器呀? 水杯 教室 酒瓶 水库 只要是…...

【阅读笔记】《硬笔书法艺术》
硬笔书法基础教程,也介绍了一些实用案例 作者: 万应均 出版社: 湖南人民出版社 笔记 CH1 运笔方式 起笔:起笔、切笔、顺峰、搭峰。 行笔:提笔、按笔、滑笔、转笔、折笔。 收笔:提收、顿收、折收。 CH2 钢笔楷书 “古人善书者…...

5.5.5、【AI技术新纪元:Spring AI解码】使用PGvector设置向量存储及进行相似性搜索
使用PGvector设置向量存储及进行相似性搜索 本节指导您如何设置PGvector VectorStore来存储文档嵌入并执行相似性搜索。 PGvector是一个开源的PostgreSQL扩展,能够支持存储和搜索机器学习生成的嵌入向量,提供查找精确和近似最近邻的功能。它设计得与PostgreSQL的其他特性无…...

EDR下的线程安全
文章目录 前记进程断链回调执行纤程内存属性修改early birdMapping后记reference 前记 触发EDR远程线程扫描关键api:createprocess、createremotethread、void(指针)、createthread 为了更加的opsec,尽量采取别的方式执行恶意代…...

洛谷刷题 | B3623 枚举排列
枚举排列 题目描述 今有 n n n 名学生,要从中选出 k k k 人排成一列拍照。 请按字典序输出所有可能的排列方式。 输入格式 仅一行,两个正整数 n , k n, k n,k。 输出格式 若干行,每行 k k k 个正整数,表示一种可能的队…...

程序员35岁会失业吗?
程序员35岁会失业吗? 35岁被认为是程序员职业生涯的分水岭,许多程序员开始担忧自己的职业发展是否会受到年龄的限制。有人担心随着年龄的增长,技术更新换代的速度会使得资深程序员难以跟上;而另一些人则认为,丰富的经…...
RabbitMQ 安装保姆级教程
目录 1.MQ引言 1.1 什么是MQ 1.2 MQ有哪些 1.3 不同MQ特点 2.RabbitMQ 的引言 2.1 RabbitMQ 2.2 RabbitMQ 的安装 2.2.1 下载 2.2.2 下载的安装包 2.2.3 安装步骤 3. RabiitMQ 配置 3.1RabbitMQ 管理命令行 3.2 web管理界面介绍 3.2.1 overview概览 3.2.2 Admin用…...
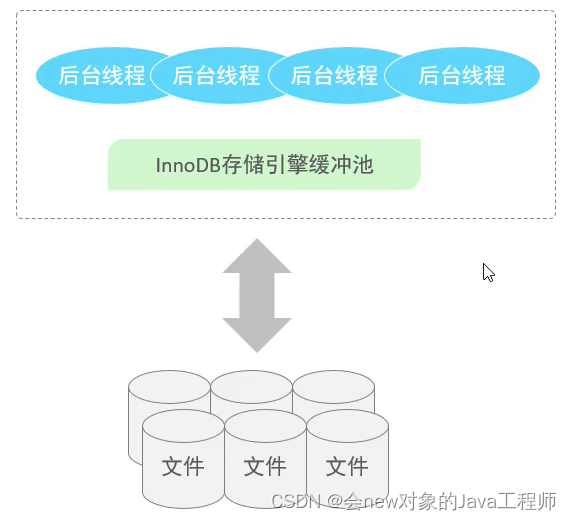
【MySQL】InnoDB引擎
逻辑结构 InnoDB存储引擎逻辑结构如图所示: Tablespace:表空间,一个数据库可以对应多个表空间。数据库中的每张表都有一个表空间,用来存放表记录、索引等数据。 Segment:段,表空间中有多个段,…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
